当前位置:网站首页>[ciscn 2021 South China]rsa writeup
[ciscn 2021 South China]rsa writeup
2022-07-06 17:22:00 【bestkasscn】
[CISCN 2021 South China ]rsa
Title Description
from flag import text,flag
import md5
from Crypto.Util.number import long_to_bytes,bytes_to_long,getPrime
assert md5.new(text).hexdigest() == flag[6:-1]
msg1 = text[:xx]
msg2 = text[xx:yy]
msg3 = text[yy:]
msg1 = bytes_to_long(msg1)
msg2 = bytes_to_long(msg2)
msg3 = bytes_to_long(msg3)
p1 = getPrime(512)
q1 = getPrime(512)
N1 = p1*q1
e1 = 3
print pow(msg1,e1,N1)
print (e1,N1)
p2 = getPrime(512)
q2 = getPrime(512)
N2 = p2*q2
e2 = 17
e3 = 65537
print pow(msg2,e2,N2)
print pow(msg2,e3,N2)
print (e2,N2)
print (e3,N2)
p3 = getPrime(512)
q3 = getPrime(512)
N3 = p3*q3
print pow(msg3,e3,N3)
print (e3,N3)
print p3>>200
We can know from the audit code ,flag == md5(text),text = msg1 + msg2 + msg3
So as long as we can solve msg1,2,3 Can solve flag
part1
p1 = getPrime(512)
q1 = getPrime(512)
N1 = p1*q1
e1 = 3
print pow(msg1,e1,N1)
print (e1,N1)
Small plaintext attack ,e Too small, resulting in the plaintext of the third power is still greater than n Small , Direct pair c1 Third power
part2
p2 = getPrime(512)
q2 = getPrime(512)
N2 = p2*q2
e2 = 17
e3 = 65537
print pow(msg2,e2,N2)
print pow(msg2,e3,N2)
print (e2,N2)
print (e3,N2)
Typical common mode attacks , The derivation process is as follows :
First , Two encryption indices are coprime :
gcd(e1,e2)=1
There is s1、s2 bring :
s1 * e1+s2 * e2=1
Again because :
c1≡m^e1 mod n
c2≡m mod n
Substitution and simplification can be obtained :
c1^s1 * c2^s2 ≡ m mod n
You can find the plaintext
part3
p3 = getPrime(512)
q3 = getPrime(512)
N3 = p3*q3
print pow(msg3,e3,N3)
print (e3,N3)
print p3>>200
Title will p3 Move right 200 position , and p3 Originally 512 position , So we use Coppersmith partial information attack Algorithm for p3 The low order of can be solved p3,q3
among ,Coppersmith partial information attack be based on sage Realization .
complete exp
from Crypto.Util.number import *
import gmpy2
from hashlib import md5
import sys
sys.setrecursionlimit(1000000)
def egcd(a, b):
if a == 0:
return b, 0, 1
else:
g, y, x = egcd(b % a, a)
return g, x - (b // a) * y, y
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
raise Exception('modular inverse does not exist')
else:
return x % m
def CommonMode(e1, e2, c1, c2, n):
s = egcd(e1, e2)
s1 = s[1]
s2 = s[2]
if s1 < 0:
s1 = - s1
c1 = modinv(c1, n)
elif s2 < 0:
s2 = - s2
c2 = modinv(c2, n)
m = (pow(c1, s1, n) * pow(c2, s2, n)) % n
return long_to_bytes(m)
c1 = 19105765285510667553313898813498220212421177527647187802549913914263968945493144633390670605116251064550364704789358830072133349108808799075021540479815182657667763617178044110939458834654922540704196330451979349353031578518479199454480458137984734402248011464467312753683234543319955893
e1 = 3
n1 = 123814470394550598363280518848914546938137731026777975885846733672494493975703069760053867471836249473290828799962586855892685902902050630018312939010564945676699712246249820341712155938398068732866646422826619477180434858148938235662092482058999079105450136181685141895955574548671667320167741641072330259009
msg1 = long_to_bytes(gmpy2.iroot(c1, e1)[0])
c2 = 54995751387258798791895413216172284653407054079765769704170763023830130981480272943338445245689293729308200574217959018462512790523622252479258419498858307898118907076773470253533344877959508766285730509067829684427375759345623701605997067135659404296663877453758701010726561824951602615501078818914410959610
c3 = 91290935267458356541959327381220067466104890455391103989639822855753797805354139741959957951983943146108552762756444475545250343766798220348240377590112854890482375744876016191773471853704014735936608436210153669829454288199838827646402742554134017280213707222338496271289894681312606239512924842845268366950
e2 = 17
e3 = 65537
n2 = 111381961169589927896512557754289420474877632607334685306667977794938824018345795836303161492076539375959731633270626091498843936401996648820451019811592594528673182109109991384472979198906744569181673282663323892346854520052840694924830064546269187849702880332522636682366270177489467478933966884097824069977
msg2 = CommonMode(e2, e3, c2, c3, n2)
c4 = 59213696442373765895948702611659756779813897653022080905635545636905434038306468935283962686059037461940227618715695875589055593696352594630107082714757036815875497138523738695066811985036315624927897081153190329636864005133757096991035607918106529151451834369442313673849563635248465014289409374291381429646
n3 = 113432930155033263769270712825121761080813952100666693606866355917116416984149165507231925180593860836255402950358327422447359200689537217528547623691586008952619063846801829802637448874451228957635707553980210685985215887107300416969549087293746310593988908287181025770739538992559714587375763131132963783147
p3_high = 7117286695925472918001071846973900342640107770214858928188419765628151478620236042882657992902
# This part of the code uses sage Go for a run
# n=113432930155033263769270712825121761080813952100666693606866355917116416984149165507231925180593860836255402950358327422447359200689537217528547623691586008952619063846801829802637448874451228957635707553980210685985215887107300416969549087293746310593988908287181025770739538992559714587375763131132963783147
# p4=7117286695925472918001071846973900342640107770214858928188419765628151478620236042882657992902# It is known that P The high
# e=65537
# pbits=512 #P Original digits
#
# kbits=pbits - p4.nbits()
# print (p4.nbits())
# p4 = p4 << kbits
# PR.<x> = PolynomialRing(Zmod(n))
# f = x + p4
# roots = f.small_roots(X=2^kbits,beta=0.4)
# # After the above functions ,n and p Has been transformed into 10 Base number
# if roots:
# p= p4 + int(roots([0]))
# print ("n",n)
# print ("p",p)
# print ("q",n/p)
p3 = 11437038763581010263116493983733546014403343859218003707512796706928880848035239990740428334091106443982769386517753703890002478698418549777553268906496423
q3 = 9918033198963879798362329507637256706010562962487329742400933192721549307087332482107381554368538995776396557446746866861247191248938339640876368268930589
d = gmpy2.invert(e3, (p3 - 1) * (q3 - 1))
msg3 = long_to_bytes(pow(c4, d, n3))
text = msg1 + msg2 + msg3
print(md5(text).hexdigest())
In the end, you get flag.
边栏推荐
猜你喜欢
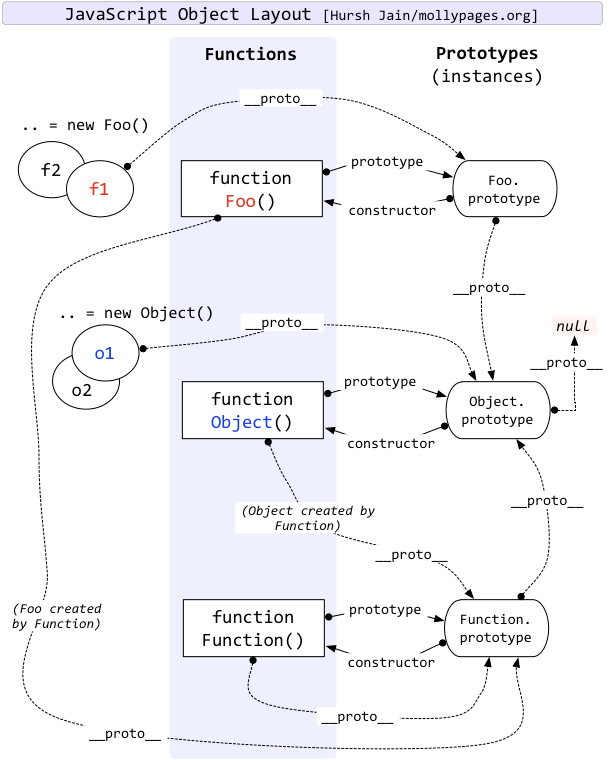
Prototype chain inheritance
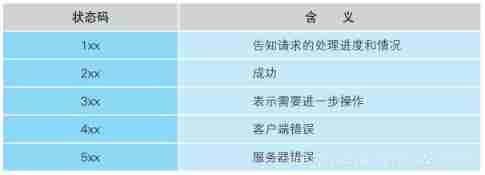
Notes on how the network is connected

Yao BanZhi and his team came together, and the competition experts gathered together. What fairy programming competition is this?
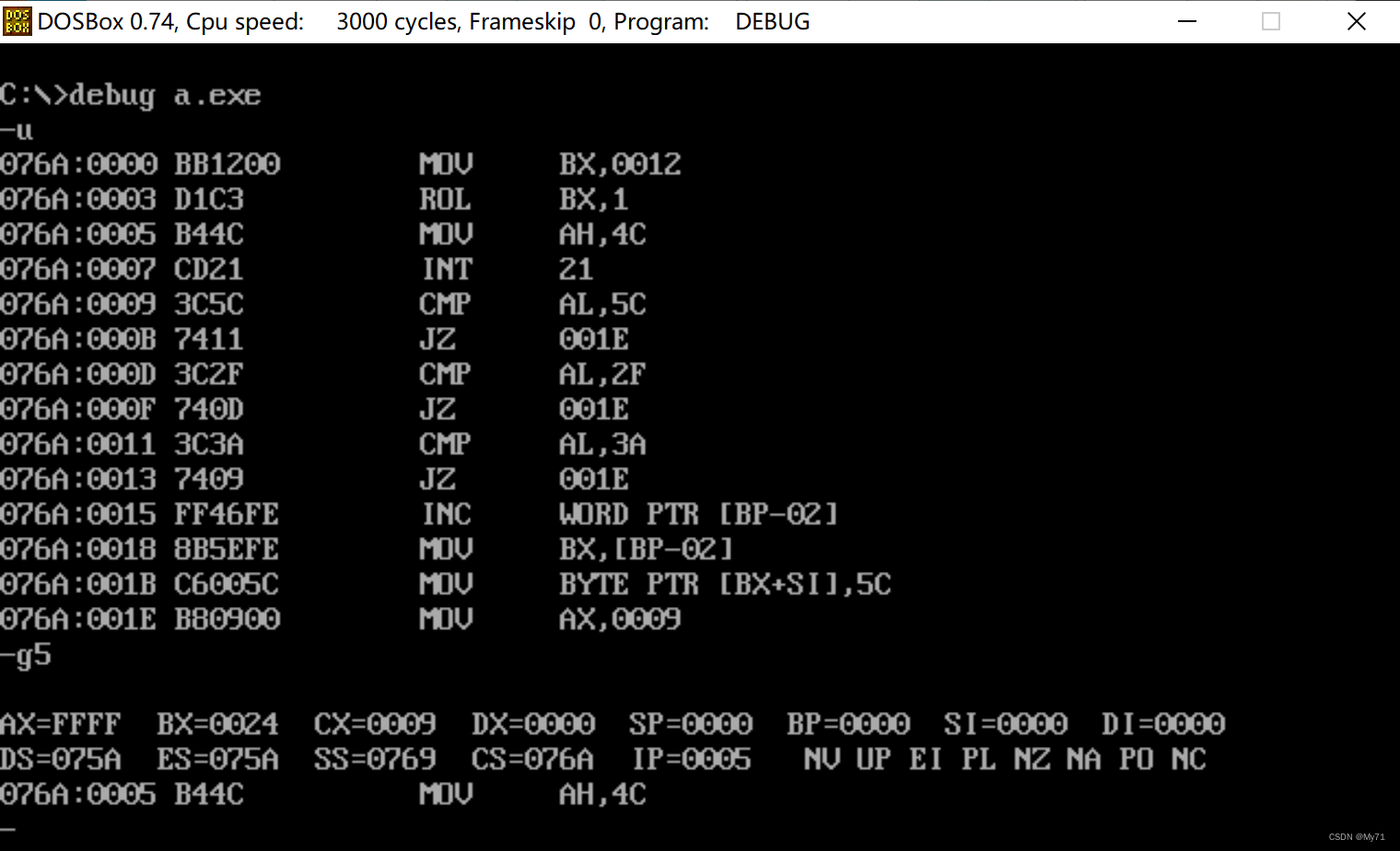
Logical operation instruction
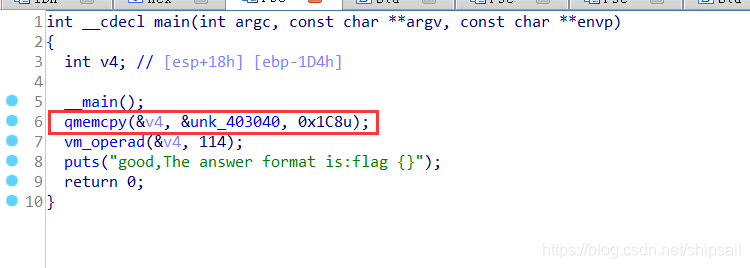
复盘网鼎杯Re-Signal Writeup

吴军三部曲见识(七) 商业的本质
MySQL日期函数

MySQL optimization notes

肖申克的救赎有感
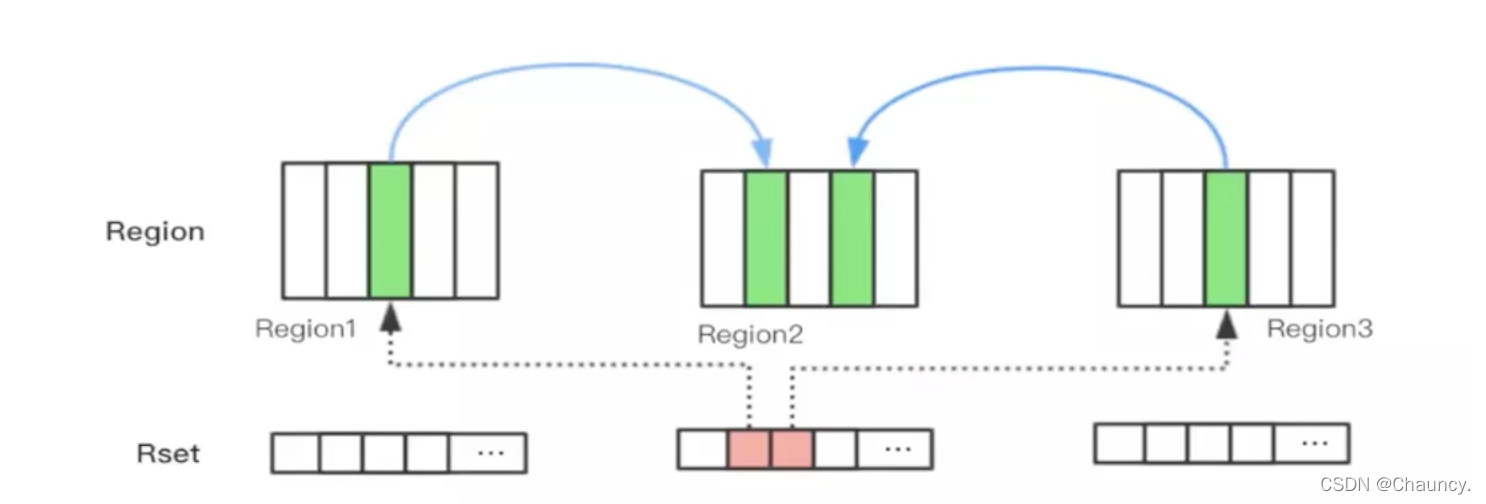
Garbage first of JVM garbage collector
随机推荐
February database ranking: how long can Oracle remain the first?
Many papers on ByteDance have been selected into CVPR 2021, and the selected dry goods are here
Activiti目录(五)驳回、重新发起、取消流程
Von Neumann architecture
【逆向】脱壳后修复IAT并关闭ASLR
Only learning C can live up to expectations top5 S1E8 | S1E9: characters and strings & arithmetic operators
数据仓库建模使用的模型以及分层介绍
After idea installs the plug-in, restart the plug-in and disappear
關於Stream和Map的巧用
1. Introduction to JVM
JVM garbage collector part 2
Akamai anti confusion
mysql的列的数据类型详解
MySQL数字函数
Ruoyi-Cloud 踩坑的BUG
MySQL字符串函数
Akamai浅谈风控原理与解决方案
肖申克的救赎有感
MySQL digital function
MySQL日期函数