当前位置:网站首页>目标检测中的BBox 回归损失函数-L2,smooth L1,IoU,GIoU,DIoU,CIoU,Focal-EIoU,Alpha-IoU,SIoU
目标检测中的BBox 回归损失函数-L2,smooth L1,IoU,GIoU,DIoU,CIoU,Focal-EIoU,Alpha-IoU,SIoU
2022-07-07 00:26:00 【cartes1us】
目标检测的两个任务,分类和位置回归,本帖将经典的位置回归损失函数总结如下,按发表时间顺序。
L1、L2、smooth L1 loss
提出smooth L1 loss的论文:
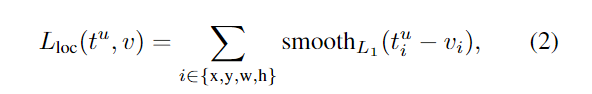
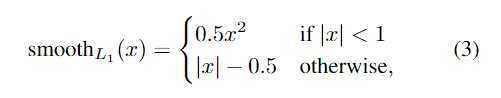
L1最低点是不可导的,所以势必不会收敛到最低点,可能会在最优解附近震荡。而L2损失容易在离群点产生梯度爆炸的问题。smooth L1则集两者的优点于一身。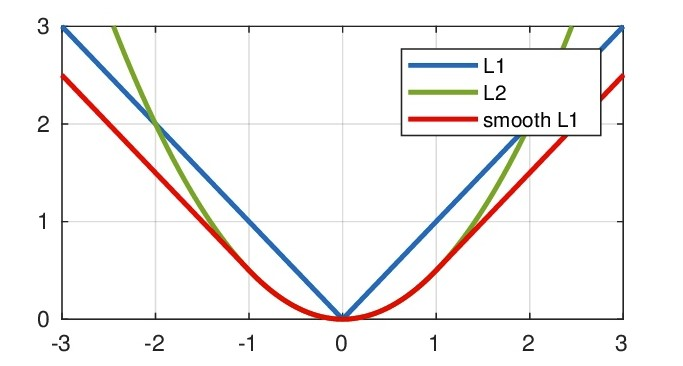
IoU loss
提出IoU loss的论文:
不论是L2还是smooth L1 loss都没有考虑到四个点的关联性和尺度不变性,这个是比较致命的缺点,当两对预测框与GT框的IoU相同时,尺度更大那一对loss会更高,或者如下图,用左下角和右上角点计算损失,L2 loss相同,但IoU却不相同。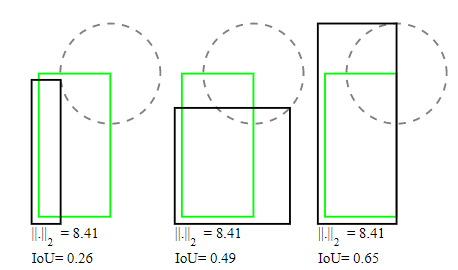
IoU损失有两种形式,后一种更为常用:
L I o U = − l n I o U L_{IoU} = -lnIoU LIoU=−lnIoU
L I o U = 1 − I o U L_{IoU} = 1-IoU LIoU=1−IoU
这样,BBox回归问题的评价指标和优化指标已经重叠统一了。
GIoU loss
提出GIoU loss 的论文:
IoU loss 最大的缺点就是两个框不相交时IoU横为0,损失恒为1,没法提供优化的梯度。
如下图(图来自CHEN), 右图的loss应该更小才对,但IoU loss却是相同的。
GIoU引入了一个最小闭包区的概念,即能将预测框和真实框包裹住的最小矩形框,其中, A c A_c Ac 为最小闭包区, u u u为预测框和真实框的并集,那么GIoU第二项的分子就是上图中白色区域,白色区域比最小闭包区的值越高,loss越高。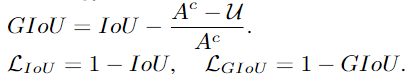
DIoU loss

而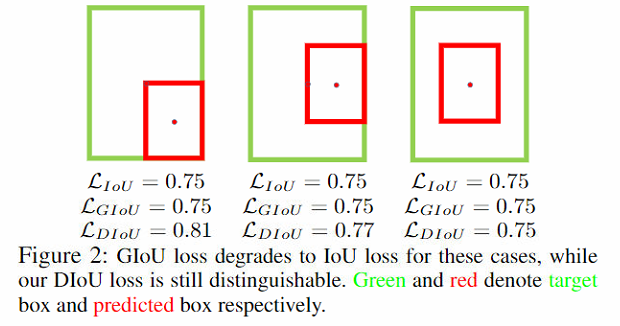
上图中三种情况下IoU和GIoU的loss均为0.75,但显然第三种情况应该是更好的预测结果,而DIoU loss就可以更精确地表示这些情况,其计算公式如下式,相比IoU损失多了一项惩罚项,是
[ 两 个 框 中 心 点 的 欧 式 距 离 最 小 闭 包 矩 形 对 角 线 长 度 ] 2 [{\frac{两个框中心点的欧式距离}{最小闭包矩形对角线长度}}]^2 [最小闭包矩形对角线长度两个框中心点的欧式距离]2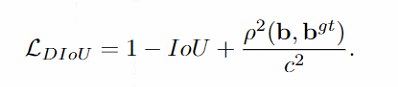
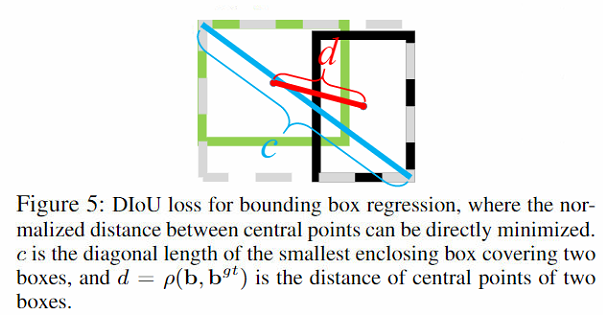
DIoU还有如下的优势:
- 因为DIoU直接最小化两个框的距离,所以收敛得比GIoU快很多,如下图示。尤其是在两个框的相对方向是垂直或水平时。
- 作为NMS的评价指标时能获得更好的效果。
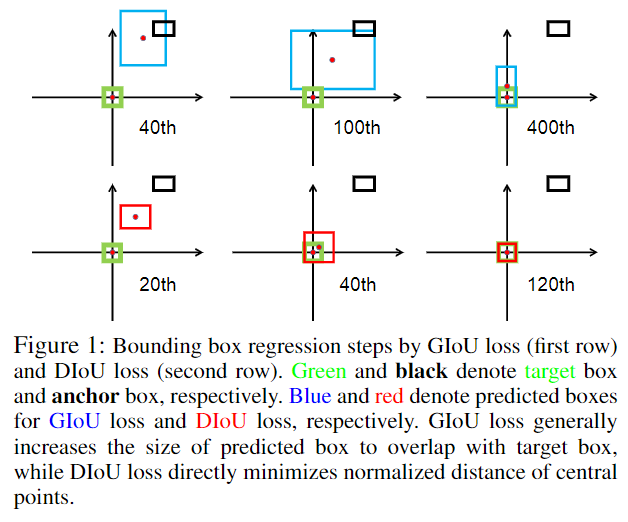
CIoU loss(Complete IoU Loss)
与DIoU loss出自同一篇文章
作者认为,好的IoU损失应该考虑三个因素:
- 相交的面积
- 中心点距离
- 长宽比
而IoU和GIoU loss只考虑了第一个因素,DIoU loss多考虑了第二个因素。
作者又提出了CIoU loss,可以更精确衡量两个框的重合度和相似度,比DIoU多了一个长宽比的惩罚项 v v v, α \alpha α是平衡系数。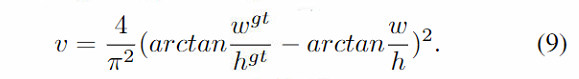
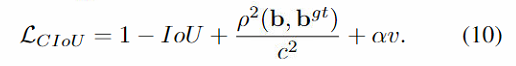
作者通过实验表明,CIoU相比其他IoU损失取得了更好的实验结果。
Focal-EIoU loss

这个损失我看知乎上大家评论不是很好啊,自己也还没细看,挖个坑。
Alpha IoU

简单说就是对IoU loss家族做了幂次运算,如下图的公式。
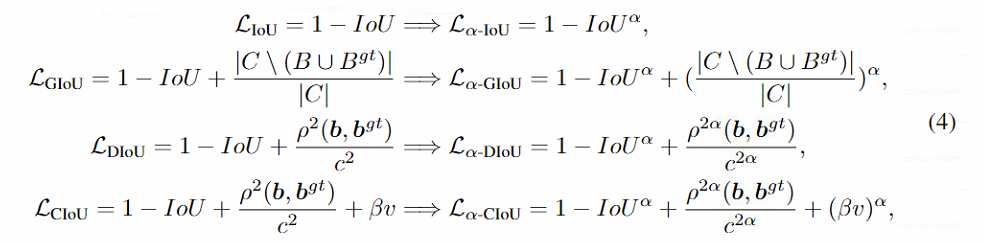
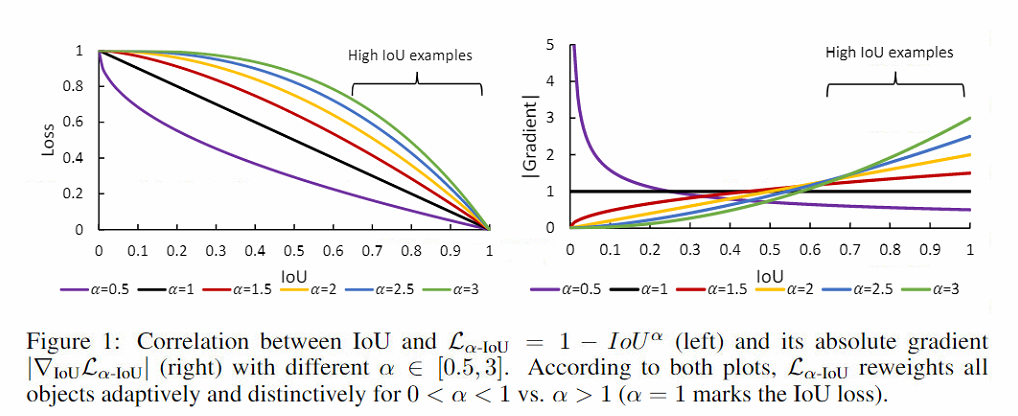
如上图,alpha-IoU可以通过自适应地提高高IoU对象的损失和梯度来提高BBox回归精度,而且对小数据集和噪声BBox提供了更好的稳健性。
SIoU loss

5月份热乎的还是预印本的新损失,但看效果比CIoU提升很多,挖个坑。
边栏推荐
猜你喜欢
集群、分布式、微服务的区别和介绍
CVE-2021-3156 漏洞复现笔记

Jhok-zbl1 leakage relay
Leakage relay jd1-100
Pytorch builds neural network to predict temperature
分布式事务解决方案之2PC
什么是消息队列?
Forkjoin is the most comprehensive and detailed explanation (from principle design to use diagram)
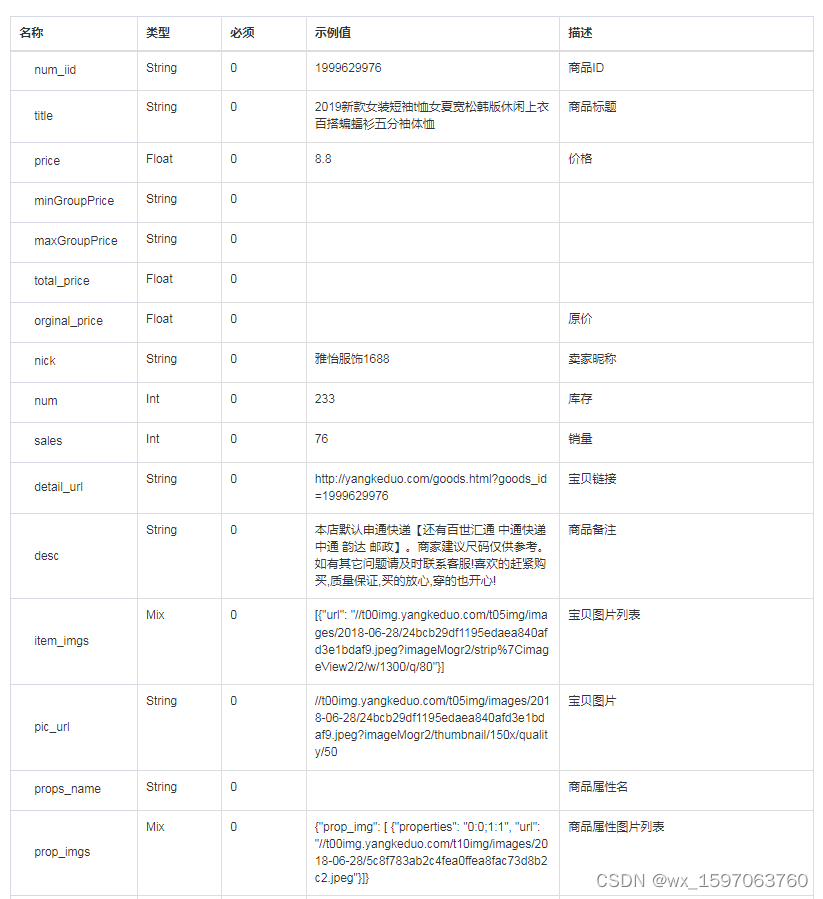
Pinduoduo product details interface, pinduoduo product basic information, pinduoduo product attribute interface
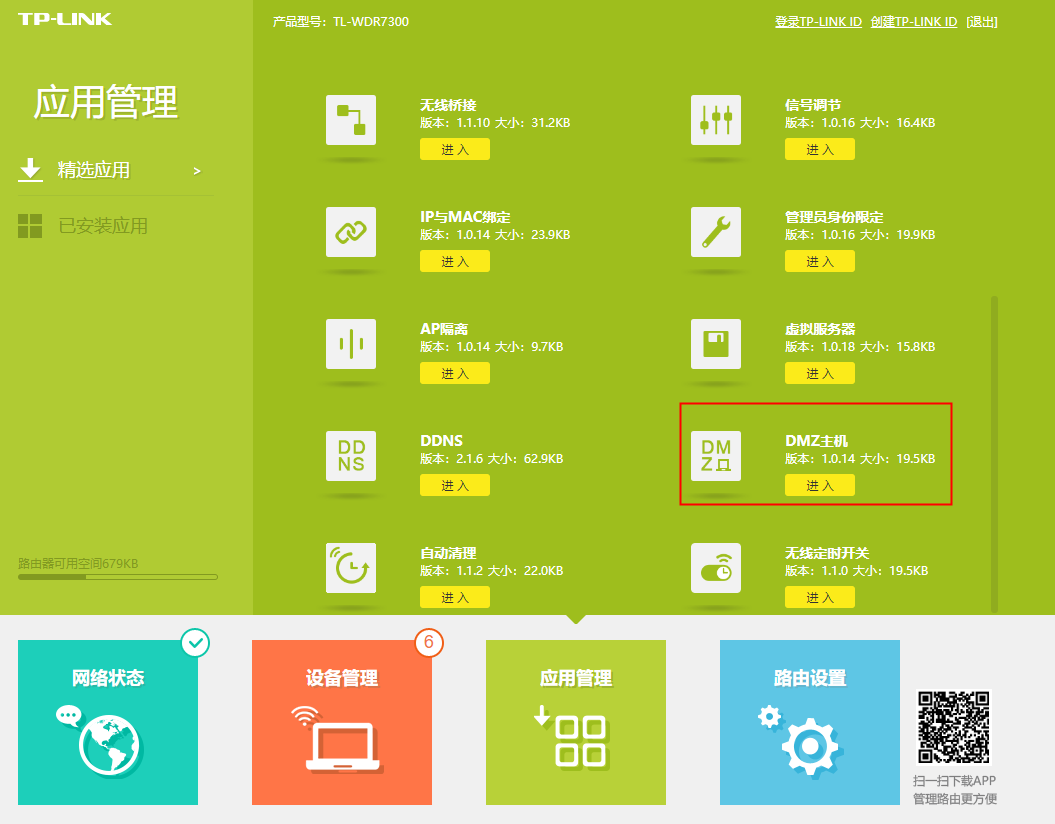
不同网段之间实现GDB远程调试功能
随机推荐
【日常训练--腾讯精选50】235. 二叉搜索树的最近公共祖先
数字IC面试总结(大厂面试经验分享)
JD commodity details page API interface, JD commodity sales API interface, JD commodity list API interface, JD app details API interface, JD details API interface, JD SKU information interface
pytorch_ 01 automatic derivation mechanism
Lombok plug-in
《2022中国低/无代码市场研究及选型评估报告》发布
Mysql-centos7 install MySQL through yum
Taobao Commodity details page API interface, Taobao Commodity List API interface, Taobao Commodity sales API interface, Taobao app details API interface, Taobao details API interface
软件测试面试技巧
[论文阅读] A Multi-branch Hybrid Transformer Network for Corneal Endothelial Cell Segmentation
Différenciation et introduction des services groupés, distribués et microservices
Realize GDB remote debugging function between different network segments
Digital innovation driven guide
Win configuration PM2 boot auto start node project
Mapbox Chinese map address
Mybaits multi table query (joint query, nested query)
Nodejs get client IP
Explication contextuelle du langage Go
Taobao store release API interface (New), Taobao oauth2.0 store commodity API interface, Taobao commodity release API interface, Taobao commodity launch API interface, a complete set of launch store i
论文阅读【Sensor-Augmented Egocentric-Video Captioning with Dynamic Modal Attention】