数字三角形模型 AcWing 1018. 最低通行费

原题链接

AcWing 1018. 最低通行费

算法标签

DP 线性DP

思路

由题意，花费时间应小于(2N−1) ， 故不能走回头路， 类似于摘花生问题。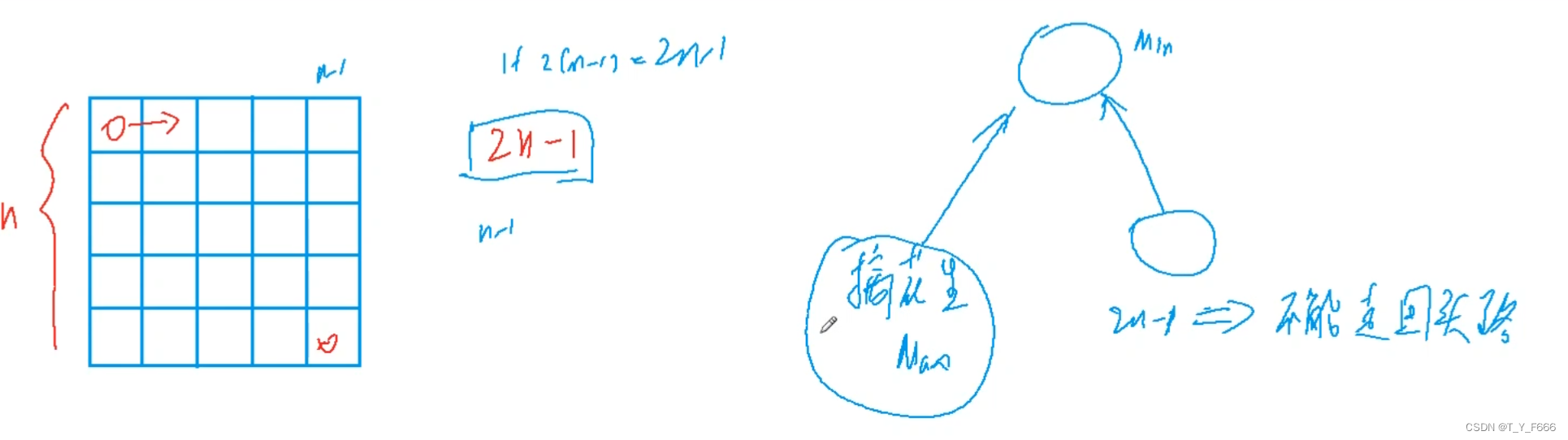

代码

#include<bits/stdc++.h>
#define int long long
#define rep(i, a, b) for(int i=a;i<b;++i)
#define Rep(i, a, b) for(int i=a;i>=b;--i)
using namespace std;
const int N = 105, INF = 0x3f3f3f3f;
int f[N][N], a[N][N];
inline int read(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}
void put(int x) {
    if(x<0) putchar('-'),x=-x;
    if(x>=10) put(x/10);
    putchar(x%10^48);
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int n=read();
	rep(i, 1, n+1){
	    rep(j, 1, n+1){
	        a[i][j]=read();
	    }
	}
	rep(i, 1, n+1){
	    rep(j, 1, n+1){
	        if(i==1&&j==1){
	            f[i][j]=a[i][j];
	        }else{
	            f[i][j]=INF;
	            if(i>1){
	                f[i][j]=min(f[i][j], f[i-1][j]+a[i][j]);
	            }
	            if(j>1){
	                f[i][j]=min(f[i][j], f[i][j-1]+a[i][j]);    
	            }
	        }
	    }
	}
	printf("%lld", f[n][n]);
    return 0;
}

原创不易
转载请标明出处
如果对你有所帮助 别忘啦点赞支持哈