当前位置:网站首页>HDU 1026 search pruning problem within the labyrinth of Ignatius and the prince I
HDU 1026 search pruning problem within the labyrinth of Ignatius and the prince I
2022-07-06 19:48:00 【Full stack programmer webmaster】
Hello everyone , I meet you again , I'm the king of the whole stack .
This problem is a typical type of problem maze extensive Search for .
I see a lot of solutions on the Internet .
There's no problem-solving analysis , Don't point out the key points . The code is more like a copy . Some analysts also have big articles to analyze . Just don't hit the key all the time , What is broad and profound , Even search and find , Analyzing differences . Why search wide image quickly , What kind of storm calls search , All wrong. . The code is copied .
Through a long period of research , It finally got through .
Although this topic can be said to be extensive search . But the key is pruning . Why? ?
Because the maze can't search all the paths simply by searching widely , Even if the maze is a little bigger, you can't find out whether there is a path . Suppose there is no conditional pruning . Don't believe it , You strictly write a wide search and search the maze path to see . Of course, you wrote a wrong search . Naturally, I got the wrong answer .
The common mistake is to expand the maze one by one, thinking it is a wide search of the maze , wrong !
The real search is to map the maze . Then search widely .
In fact, the real key is pruning :
Pruning thinking is to think about when it should be extended to the next grid ? Whether the lattice is legal or not must be able to expand ? Of course not. , It is necessary to prune according to the meaning of the topic . The meaning of this question is to find the path with the smallest time . Therefore, it can be thought that it should be decided by time comparison whether it needs to be extended to the next grid .
That is, if the next lattice is possible to find a better solution, it will expand . Otherwise, do not expand .
After such a pruning . You can use the so-called wide search .
So why this topic . Or it can be said that the topic of this topic type cannot use deep search ?
Because the above pruning condition is that each layer is pruned , Suppose you use deep search , Then this pruning condition cannot be used .
Another way is to use priority queues . Give priority to expanding the lattice with the current minimum time . Then you don't have to search the next box repeatedly . This is also the use of the above pruning ideas .
Just understand the key pruning points above , Then this kind of problem can be solved at will .
As for the recording path of this question, it is the test of programming skills , Needless to say, what ideas . No, just say that the coding ability is not good .
Maybe some people who don't understand analysis also hit the code right , Maybe he's lucky . Maybe he is really a genius !
Anyway, the probability is very low , The greatest chance is that his code is copied .
#include <stdio.h>
#include <vector>
#include <string.h>
#include <algorithm>
#include <iostream>
#include <string>
#include <limits.h>
#include <stack>
#include <queue>
#include <set>
#include <map>
using namespace std;
/*
Key understanding : Only when the next grid updates the minimum value does it need to be extended to this grid . Otherwise, there is no need to expand to this lattice . This is also equivalent to the pruning point of guangsearch . I can't understand this . There is no thorough understanding of this problem .*/namespace IgnatiusandthePrincessI1026{const int MAX_N = 101;char Maze[MAX_N][MAX_N];int dx[] = {-1, 0, 1, 0}, dy[] = {0, -1, 0, 1};struct Node{ int sec, x, y; Node *p;};Node mazeRec[MAX_N][MAX_N];int N, M;inline bool isLegal(int r, int c){ return 0<=r && 0<=c && r<N && c<M && Maze[r][c] != 'X';}inline int getSec(int r, int c){ if (Maze[r][c] == '.') return 1; return Maze[r][c] - '0' + 1;}void getPath(){ for (int i = 0; i < N; i++) { for (int j = 0; j < M; j++) { mazeRec[i][j].sec = INT_MAX; mazeRec[i][j].x = i, mazeRec[i][j].y = j; mazeRec[i][j].p = NULL; } } queue<Node *> qu; Node *p = &mazeRec[N-1][M-1]; // Pay attention to the calculation error :p->sec = Maze[N-1][M-1] or = getSec(N-1, M-1) p->sec = getSec(N-1, M-1)-1;// The end may also be an enemy , The starting point stipulates invincible qu.push(p); while (!qu.empty()) { p = qu.front(); qu.pop(); for (int i = 0; i < 4; i++) { int tx = p->x + dx[i], ty = p->y + dy[i]; if (!isLegal(tx, ty)) continue; int sec = getSec(tx, ty); Node *tmp = &mazeRec[tx][ty]; if (p->sec+sec < tmp->sec) { tmp->sec = p->sec+sec; tmp->p = p; qu.push(tmp); } /* Key understanding : Only when the next grid updates the minimum value does it need to be extended to this grid . Otherwise, there is no need to expand to this lattice . This is also equivalent to the pruning point of guangsearch . I can't understand this , There is no thorough understanding of this problem .*//* All kinds of mistakes and lessons ! qu.push(tmp); tmp.vis = true; // Multiple errors else. Logic error else tmp->vis = true //Maze[tx][ty] = 'X'; tmp.sec = p.sec+sec; tmp.p = &mazeRec[p.x][p.y]; // error :tmp->p = p; // error :tmp->sec = min(tmp->sec, p->sec+sec);*/ } }}int main(){ while (~scanf("%d %d", &N, &M)) { while (getchar() != '\n'); for (int i = 0; i < N; i++) { gets(Maze[i]); } getPath(); Node *p = &mazeRec[0][0]; if (p->sec == INT_MAX) puts("God please help our poor hero."); else { printf("It takes %d seconds to reach the target position, let me show you the way.\n", p->sec); int s = 1; for (; p->p; p = p->p) { int x = p->p->x, y = p->p->y; printf("%ds:(%d,%d)->(%d,%d)\n", s++, p->x, p->y, x, y); if (Maze[x][y] == '.') continue; int fig = Maze[x][y] - '0';// Fewer mistakes -'0' for (int i = 0; i < fig; i++) { printf("%ds:FIGHT AT (%d,%d)\n", s++, x, y); } } } puts("FINISH"); } return 0;}Copyright notice : The author Jing Xin . Landscape space address :http://blog.csdn.net/kenden23/. Reprinted only with the consent of the author .
Publisher : Full stack programmer stack length , Reprint please indicate the source :https://javaforall.cn/117152.html Link to the original text :https://javaforall.cn
边栏推荐
- Chic Lang: attributeerror: partially initialized module 'CV2' has no attribute 'GAPI_ wip_ gst_ GStreamerPipe
- From spark csc. csr_ Matrix generate adjacency matrix
- 力扣101题:对称二叉树
- POJ1149 PIGS 【最大流量】
- [calculating emotion and thought] floor sweeper, typist, information panic and Oppenheimer
- The slave i/o thread stops because master and slave have equal MySQL serv
- Using clip path to draw irregular graphics
- 深入浅出,面试突击版
- Mysql Information Schema 學習(一)--通用錶
- Example of shutter text component
猜你喜欢
It's super detailed in history. It's too late for you to read this information if you want to find a job

Carte de réflexion + code source + notes + projet, saut d'octets + jd + 360 + tri des questions d'entrevue Netease

Mind map + source code + Notes + project, ByteDance + JD +360+ Netease interview question sorting
![[infrastructure] deployment and configuration of Flink / Flink CDC (MySQL / es)](/img/1e/b270a81c8457f1eae34f55c004a01a.png)
[infrastructure] deployment and configuration of Flink / Flink CDC (MySQL / es)
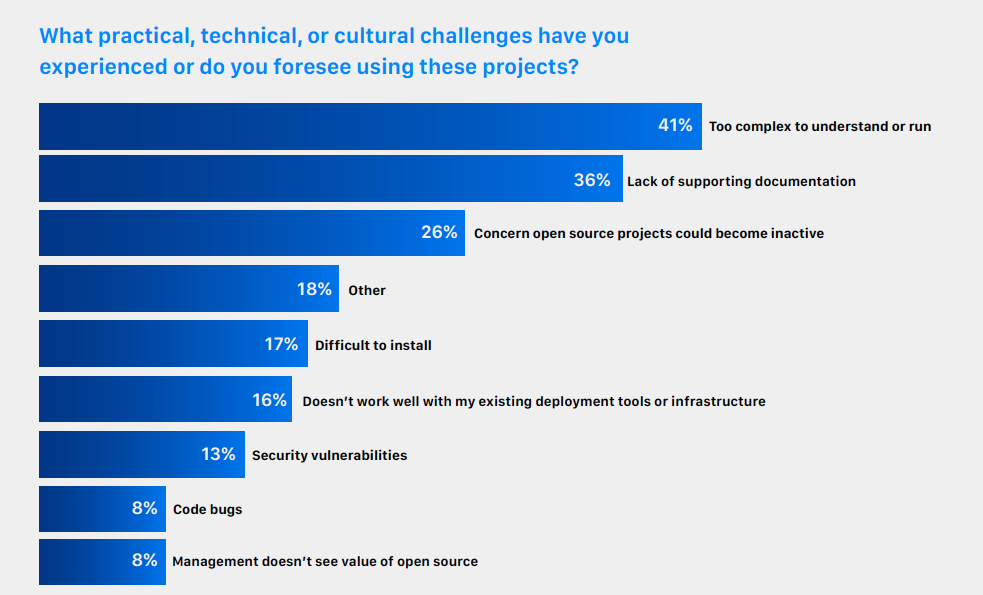
【翻译】云原生观察能力微调查。普罗米修斯引领潮流,但要了解系统的健康状况仍有障碍...

MySQL information schema learning (II) -- InnoDB table

冒烟测试怎么做
在解决了 2961 个用户反馈后,我做出了这样的改变...
![[translation] linkerd's adoption rate in Europe and North America exceeded istio, with an increase of 118% in 2021.](/img/09/106adc222c06cbd2f4f66cf475cce2.jpg)
[translation] linkerd's adoption rate in Europe and North America exceeded istio, with an increase of 118% in 2021.
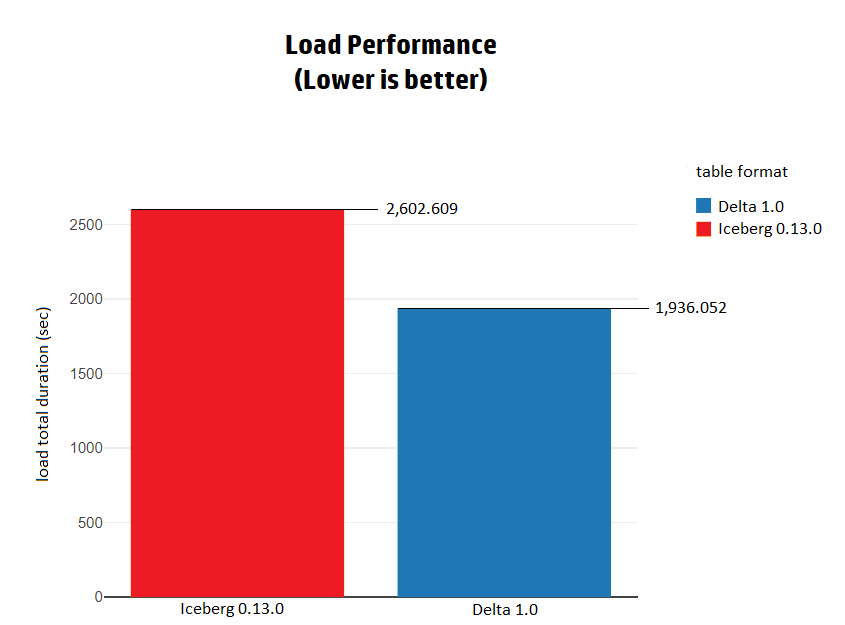
Hudi vs Delta vs Iceberg
随机推荐
Leetcode 30. 串联所有单词的子串
学习探索-使用伪元素清除浮动元素造成的高度坍塌
【翻译】云原生观察能力微调查。普罗米修斯引领潮流,但要了解系统的健康状况仍有障碍...
[玩转Linux] [Docker] MySQL安装和配置
Hudi vs Delta vs Iceberg
蓝桥杯 微生物增殖 C语言
MySql必知必会学习
After solving 2961 user feedback, I made such a change
通俗的讲解,带你入门协程
It's enough to read this article to analyze the principle in depth
潇洒郎: AttributeError: partially initialized module ‘cv2‘ has no attribute ‘gapi_wip_gst_GStreamerPipe
DOM operation
Example of applying fonts to flutter
接雨水问题解析
今日直播 | “人玑协同 未来已来”2022弘玑生态伙伴大会蓄势待发
DaGAN论文解读
学习探索-函数防抖
Chic Lang: attributeerror: partially initialized module 'CV2' has no attribute 'GAPI_ wip_ gst_ GStreamerPipe
Alibaba数据源Druid可视化监控配置
map的使用(列表的数据赋值到表单,json逗号隔开显示赋值)