当前位置:网站首页>POJ1149 PIGS 【最大流量】
POJ1149 PIGS 【最大流量】
2022-07-06 11:47:00 【全栈程序员站长】
大家好,又见面了,我是全栈君。
PIGS
Time Limit: 1000MS | Memory Limit: 10000K | |
|---|---|---|
Total Submissions: 16555 | Accepted: 7416 |
Description
Mirko works on a pig farm that consists of M locked pig-houses and Mirko can’t unlock any pighouse because he doesn’t have the keys. Customers come to the farm one after another. Each of them has keys to some pig-houses and wants to buy a certain number of pigs. All data concerning customers planning to visit the farm on that particular day are available to Mirko early in the morning so that he can make a sales-plan in order to maximize the number of pigs sold. More precisely, the procedure is as following: the customer arrives, opens all pig-houses to which he has the key, Mirko sells a certain number of pigs from all the unlocked pig-houses to him, and, if Mirko wants, he can redistribute the remaining pigs across the unlocked pig-houses. An unlimited number of pigs can be placed in every pig-house. Write a program that will find the maximum number of pigs that he can sell on that day.
Input
The first line of input contains two integers M and N, 1 <= M <= 1000, 1 <= N <= 100, number of pighouses and number of customers. Pig houses are numbered from 1 to M and customers are numbered from 1 to N. The next line contains M integeres, for each pig-house initial number of pigs. The number of pigs in each pig-house is greater or equal to 0 and less or equal to 1000. The next N lines contains records about the customers in the following form ( record about the i-th customer is written in the (i+2)-th line): A K1 K2 … KA B It means that this customer has key to the pig-houses marked with the numbers K1, K2, …, KA (sorted nondecreasingly ) and that he wants to buy B pigs. Numbers A and B can be equal to 0.
Output
The first and only line of the output should contain the number of sold pigs.
Sample Input
3 3
3 1 10
2 1 2 2
2 1 3 3
1 2 6Sample Output
7Source
Croatia OI 2002 Final Exam – First day
题目大意 Mirko养着一些猪 猪关在一些猪圈里面 猪圈是锁着的 他自己没有钥匙(汗) 仅仅有要来买猪的顾客才有钥匙 顾客依次来 每一个顾客会用他的钥匙打开一些猪圈 买 走一些猪 然后锁上 在锁上之前 Mirko有机会又一次分配这几个已打开猪圈 的猪 如今给出一開始每一个猪圈的猪数 每一个顾客全部的钥匙 和要买走的猪数 问Mirko最多能卖掉几头猪
题解:对于每一个猪圈的第一个购买的人,加入一条源点到这个人的边,权为这个猪圈的猪数,对于后来的且想要购买该猪圈的人。加入一条第一个购买该猪圈的人到该人的边。权为inf,然后加入每一个人到汇点一条边,权值为该人想要购买的猪的头数。至此,构图完毕。
#include <stdio.h>
#include <string.h>
#define inf 0x3fffffff
#define maxn 110
#define maxm 1002
int pig[maxm], m, n, sink;
int G[maxn][maxn], queue[maxn];
bool vis[maxn]; int Layer[maxn];
bool countLayer() {
memset(Layer, 0, sizeof(Layer));
int id = 0, front = 0, now, i;
Layer[0] = 1; queue[id++] = 0;
while(front < id) {
now = queue[front++];
for(i = 0; i <= sink; ++i)
if(G[now][i] && !Layer[i]) {
Layer[i] = Layer[now] + 1;
if(i == sink) return true;
else queue[id++] = i;
}
}
return false;
}
int Dinic() {
int minCut, pos, maxFlow = 0;
int i, id = 0, u, v, now;
while(countLayer()) {
memset(vis, 0, sizeof(vis));
vis[0] = 1; queue[id++] = 0;
while(id) {
now = queue[id - 1];
if(now == sink) {
minCut = inf;
for(i = 1; i < id; ++i) {
u = queue[i - 1];
v = queue[i];
if(G[u][v] < minCut) {
minCut = G[u][v];
pos = u;
}
}
maxFlow += minCut;
for(i = 1; i < id; ++i) {
u = queue[i - 1];
v = queue[i];
G[u][v] -= minCut;
G[v][u] += minCut;
}
while(queue[id - 1] != pos)
vis[queue[--id]] = 0;
} else {
for(i = 0; i <= sink; ++i) {
if(G[now][i] && Layer[now] + 1 == Layer[i] && !vis[i]) {
vis[i] = 1; queue[id++] = i; break;
}
}
if(i > sink) --id;
}
}
}
return maxFlow;
}
int main() {
//freopen("stdin.txt", "r", stdin);
int i, keys, num;
while(scanf("%d%d", &m, &n) == 2) {
sink = n + 1;
for(i = 1; i <= m; ++i)
scanf("%d", &pig[i]);
memset(G, 0, sizeof(G));
for(i = 1; i <= n; ++i) {
scanf("%d", &keys);
while(keys--) {
scanf("%d", &num);
if(pig[num] >= 0) {
G[0][i] += pig[num]; // 0 is source
pig[num] = -i; // 这里是标记第num个猪圈联通的第一个人
} else G[-pig[num]][i] = inf;
}
scanf("%d", &G[i][sink]);
}
printf("%d\n", Dinic());
}
return 0;
}2015.4.20
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 105;
const int inf = 0x3f3f3f3f;
int G[maxn][maxn], M, N, S, T;
int pigHouse[maxn*10];
int Dinic(int s, int t);
void getMap()
{
memset(G, 0, sizeof(G));
S = 0; T = N + 1;
int i, j, K, pos;
for (i = 1; i <= M; ++i)
scanf("%d", &pigHouse[i]);
for (i = 1; i <= N; ++i) {
scanf("%d", &K);
while (K--) {
scanf("%d", &pos);
if (pigHouse[pos] >= 0) {
G[S][i] += pigHouse[pos];
pigHouse[pos] = -i;
} else {
G[-pigHouse[pos]][i] = inf;
}
}
scanf("%d", &G[i][T]);
}
}
void solve()
{
cout << Dinic(S, T) << endl;
}
int main()
{
while (cin >> M >> N) {
getMap();
solve();
}
return 0;
}
int queue[maxn];
bool vis[maxn]; int Layer[maxn];
bool countLayer(int s, int t) {
memset(Layer, 0, sizeof(Layer));
int id = 0, front = 0, now, i;
Layer[s] = 1; queue[id++] = s;
while(front < id) {
now = queue[front++];
for(i = s; i <= t; ++i)
if(G[now][i] && !Layer[i]) {
Layer[i] = Layer[now] + 1;
if(i == t) return true;
else queue[id++] = i;
}
}
return false;
}
// 源点,汇点,源点编号必须最小,汇点编号必须最大
int Dinic(int s, int t) {
int minCut, pos, maxFlow = 0;
int i, id = 0, u, v, now;
while(countLayer(s, t)) {
memset(vis, 0, sizeof(vis));
vis[s] = true; queue[id++] = s;
while(id) {
now = queue[id - 1];
if(now == t) {
minCut = inf;
for(i = 1; i < id; ++i) {
u = queue[i - 1];
v = queue[i];
if(G[u][v] < minCut) {
minCut = G[u][v];
pos = u;
}
}
maxFlow += minCut;
for(i = 1; i < id; ++i) {
u = queue[i - 1];
v = queue[i];
G[u][v] -= minCut;
G[v][u] += minCut;
}
while(queue[id - 1] != pos)
vis[queue[--id]] = false;
} else {
for(i = s; i <= t; ++i) {
if(G[now][i] && Layer[now] + 1 == Layer[i] && !vis[i]) {
vis[i] = 1; queue[id++] = i; break;
}
}
if(i > t) --id;
}
}
}
return maxFlow;
}版权声明:本文博客原创文章,博客,未经同意,不得转载。
发布者:全栈程序员栈长,转载请注明出处:https://javaforall.cn/117136.html原文链接:https://javaforall.cn
边栏推荐
- 利用 clip-path 绘制不规则的图形
- Understand yolov1 Part II non maximum suppression (NMS) in prediction stage
- Application of clock wheel in RPC
- 腾讯T3手把手教你,真的太香了
- Using clip path to draw irregular graphics
- 【基础架构】Flink/Flink-CDC的部署和配置(MySQL / ES)
- Druid 数据库连接池 详解
- Alibaba data source Druid visual monitoring configuration
- Is not a drawable (color or path): the vector graph downloaded externally cannot be called when it is put into mipmap, and the calling error program crashes
- Microservice architecture debate between radical technologists vs Project conservatives
猜你喜欢

利用 clip-path 绘制不规则的图形
Swiftui game source code Encyclopedia of Snake game based on geometryreader and preference
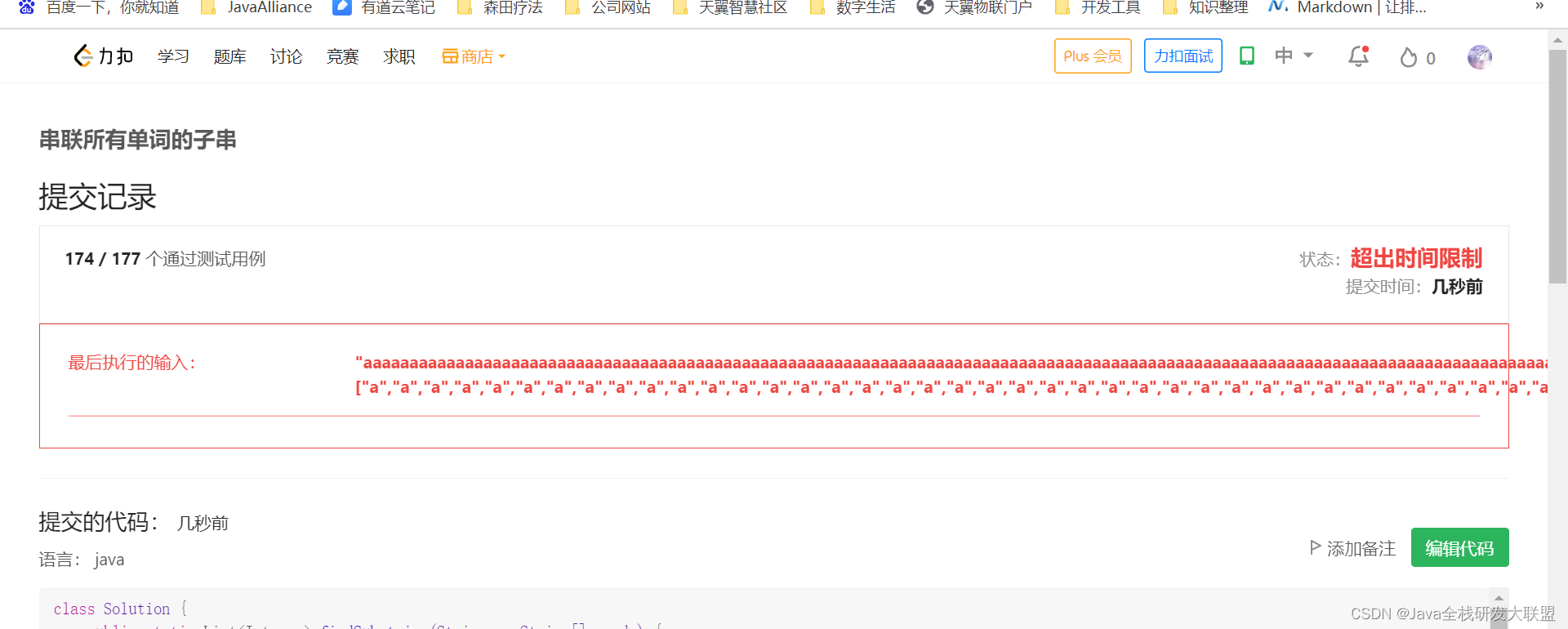
Leetcode 30. Concatenate substrings of all words
Mysql Information Schema 學習(一)--通用錶
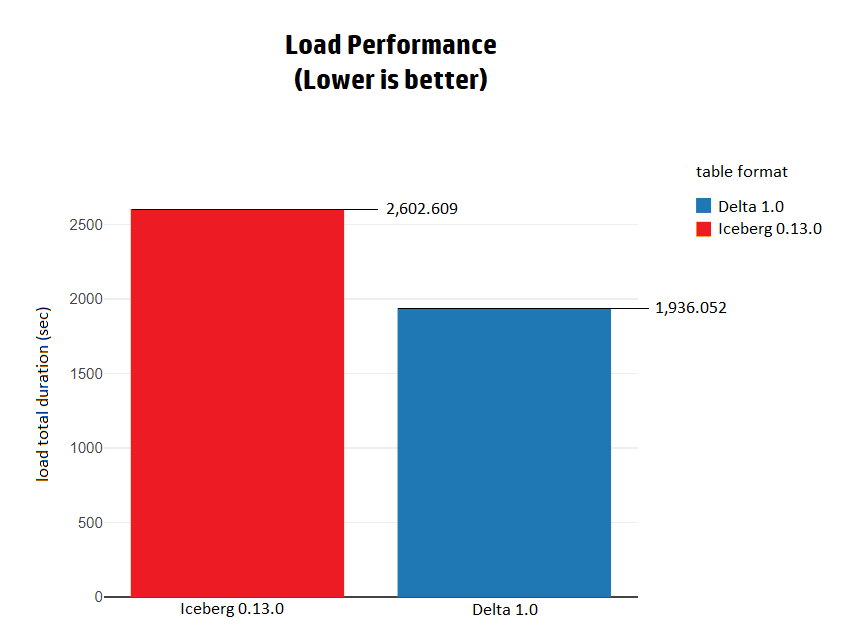
Hudi vs Delta vs Iceberg

Tencent Android interview must ask, 10 years of Android development experience
【基础架构】Flink/Flink-CDC的部署和配置(MySQL / ES)
Zero foundation entry polardb-x: build a highly available system and link the big data screen

Leetcode 30. 串联所有单词的子串
Li Kou 101: symmetric binary tree
随机推荐
零基础入门PolarDB-X:搭建高可用系统并联动数据大屏
MySQL must know and learn
How to do smoke test
Unbalance balance (dynamic programming, DP)
Learning and Exploration - function anti shake
The "white paper on the panorama of the digital economy" has been released with great emphasis on the digitalization of insurance
Cereals Mall - Distributed Advanced p129~p339 (end)
【翻译】数字内幕。KubeCon + CloudNativeCon在2022年欧洲的选择过程
腾讯T2大牛亲自讲解,跳槽薪资翻倍
Analysis of rainwater connection
Understand yolov1 Part II non maximum suppression (NMS) in prediction stage
Learning and Exploration - Seamless rotation map
Dark horse -- redis
Chic Lang: attributeerror: partially initialized module 'CV2' has no attribute 'GAPI_ wip_ gst_ GStreamerPipe
Hudi vs Delta vs Iceberg
How to customize animation avatars? These six free online cartoon avatar generators are exciting at a glance!
121. The best time to buy and sell stocks
Leetcode 30. Concatenate substrings of all words
zabbix 代理服务器 与 zabbix-snmp 监控
1805. 字符串中不同整数的数目