The first time to tear the code by hand, how to solve the problem of full arrangement

面试官：Here is a programming question,need you to do it……

求职者：哎,好

面试官：probably for you 10 分钟

7 minutes later……

求职者：面试官,For this question I think it is possible to usefor循环,First find the number of times you need to loop,Then the amount

面试官：Is there any way to solve this problem using recursion?

求职者：这个呢…

一、Brainless loop solution？

拿到这个问题,Of course my first thought was for 循环,比如这样：

for(int i = 1; i < n+1; i++){
    
	for(int j = 1; j < n+1; j++){
    
		for(int k = 1; k < n+1; k++){
    
			……From now on in endless loop
		}
	}
}

可是,问题大了,How many cycles are there？n 个？

又或者是 while loop to control the number of loops：

while(i < n){
    
	for(int j = 1; j < n+1; j++){
    
		……so in the cycle again
	}
	i++;
}

十分钟内,The whole mind is how to control the number of loops to solve this problem.其实,If you understand the backtracking algorithm,not to take for Loop to deal with the interviewer,Let's analyze this problem.

二、全排列的个数

首先,Questions about the whole arrangement,It is easy to get the number of answers to the question as n！个：

当 n = 2 时,全排列的个数为 2 个：

[1,2]、[2,1]

当 n = 3 时,全排列的个数为 3*2 ,即 6 个：

[1,2,3]、[1,3,2]、[2,1,3]、[2,3,1]、[3,1,2]、[3,2,1]

当 n = 4 时,The total number of slices is 4*3*2 ,即 24 个

[1, 2, 3, 4]、[1, 2, 4, 3]、[1, 3, 2, 4]、[1, 3, 4, 2]、[1, 4, 2, 3]、[1, 4, 3, 2]、
[2, 1, 3, 4]、[2, 1, 4, 3]、[2, 3, 1, 4]、[2, 3, 4, 1]、[2, 4, 1, 3]、[2, 4, 3, 1]、
[3, 1, 2, 4]、[3, 1, 4, 2]、[3, 2, 1, 4]、[3, 2, 4, 1]、[3, 4, 1, 2]、[3, 4, 2, 1]、
[4, 1, 2, 3]、[4, 1, 3, 2]、[4, 2, 1, 3]、[4, 2, 3, 1]、[4, 3, 1, 2]、[4, 3, 2, 1]

很容易推出 n 个数字时,全排列的个数为 n! 个.

三、Backtracking algorithm for the problem solving

Next, we use the backtracking algorithm to solve this problem.,还是比较简单的.首先,We need to construct a fully permuted solution space.Similarly, here we first study the smaller problems,假设 n 为 3 solution space：

The solution space of the backtracking algorithm is a polytree,Usually the root node is empty.In this polytree,Leaf nodes are called non-extendable nodes,Non-leaf nodes are called extensible nodes.

接下来,You need to pass depth traversal traversal many forks tree,Each traversal to the leaf node,to get a corresponding solution.

Backtracking happens during traversal,When encountering a non-scalable node,You need to go back to the tree layer,Continue to traverse other extensible nodes.

Then you can use the code to achieve,There are two main ways to implement the backtracking algorithm：

1、Recursive implementation of backtracking algorithm

  递归实现思路：function self-tuning,Continue to traverse the depth of the tree through the self-tuning function;而通过 for 循环,to find the right node,and temporarily in the result set.递归终止时,i.e. get a complete result！

/** * * @param t 起始层数,初始值为 1 * @param n 数的个数,the last layer of the tree * @param ls 结果集 */
public static void backTrack(int t, int n, ArrayList<Integer> ls) {
    
		if(t > n) {
    
			System.out.println(ls.toString());
		}else {
    
			for(int i = 1; i < n+1; i++) {
    
				if(ls.contains(i))
					continue;
				else
					ls.add(i);
				backTrack(t+1, n, ls);
				ls.remove(t-1);
			}

		}
}

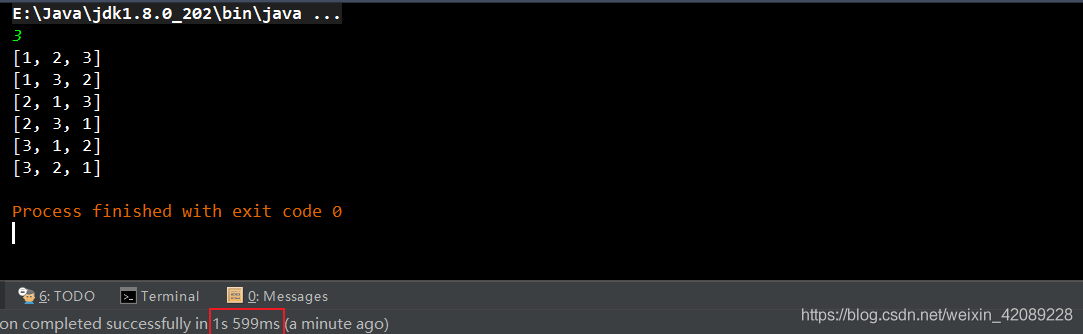
Below is the abstract procedure of recursive call：

观察这个过程,You will find that recursion has a natural advantage over backtracking algorithms,In other words, recursion is a process of continuous backtracking.;The iterative implementation of the backtracking algorithm is more difficult to understand.

2、Iteratively implement the backtracking algorithm

  递归实现思路：Backtracking using iteration,like plunging into a dead end,Then step back,After back again into a dead end.until back out of the alley,Exit the whole back process.

/** * @param n 数的个数 * @param ls 结果集 */
public static void iterativeBacktrack(int n, ArrayList<Integer> ls) {
    
		int t = 1;
		int left = 1;
		while(t > 0) {
    
			if(left <= n) {
    
				for(int i = left; i <= n; i++) {
    
					if(ls.contains(i)) {
    
						continue;
					}else {
    
						if(ls.size() == t){
    
							ls.set(t-1, i);
						}else{
    
							ls.add(t-1, i);
						}
						i = 0;
					}
					if(t == n) {
    
						System.out.println(ls.toString());
					}else {
    
						t++;
						i=0;
					}
				}
			}
			if (t > 0){
    
				ls.remove(t-1);
			}
			t--;
			if(t > 0)
				left = ls.get(t-1);
		}
}

---

Actually there is backtracking algorithm最后一步,Trim excess branches with constraints and boundary control,To improve the efficiency of the backtracking algorithm.这里,no pruning……