当前位置:网站首页>LeetCode 1561. The maximum number of coins you can get
LeetCode 1561. The maximum number of coins you can get
2022-07-06 16:42:00 【Daylight629】
1561. The maximum number of coins you can get
Yes 3n A pile of coins in different numbers , You and your friends are going to divide coins in the following way :
- In every round , You will choose arbitrarily 3 Pile coins ( Not necessarily continuous ).
- Alice The pile with the largest number of coins will be taken away .
- You will take away the pile with the second largest number of coins .
- Bob Will take the last pile .
- Repeat the process , Until there are no more coins .
Give you an array of integers piles , among piles[i] It's No i The number of coins in the pile .
Returns the maximum number of coins you can get .
Example 1:
Input :piles = [2,4,1,2,7,8]
Output :9
explain : elect (2, 7, 8) ,Alice Take away 8 The pile of coins , You take it 7 The pile of coins ,Bob Take the last pile .
elect (1, 2, 4) , Alice Take away 4 The pile of coins , You take it 2 The pile of coins ,Bob Take the last pile .
The maximum number of coins you can get :7 + 2 = 9.
Consider the other case , If you choose (1, 2, 8) and (2, 4, 7) , You can only get 2 + 4 = 6 Coin , This is not the optimal solution .
Example 2:
Input :piles = [2,4,5]
Output :4
Example 3:
Input :piles = [9,8,7,6,5,1,2,3,4]
Output :18
Tips :
3 <= piles.length <= 10^5piles.length % 3 == 01 <= piles[i] <= 10^4
Two 、 Method 1
greedy , By sorting , Ahead 1/3 All are Bob Of , We reverse the order , Take the second largest pile
class Solution {
public int maxCoins(int[] piles) {
Arrays.sort(piles);
int round = piles.length / 3;
int idx = piles.length - 2;
int res = 0;
for (int i = 0; i < round; i++) {
res += piles[idx];
idx -= 2;
}
return res;
}
}
Complexity analysis
Time complexity :O(nlogn), among nn Is the length of the array divided by 3( That is, the length of the array is 3n). The time complexity of sorting is O(3nlog3n)=O(3n(log3+logn))=O(nlogn), The time complexity of traversing the array to calculate the maximum number of coins is O(n), So the total time complexity is O(nlogn).
Spatial complexity :O(logn).
边栏推荐
- useEffect,函數組件掛載和卸載時觸發
- Story of [Kun Jintong]: talk about Chinese character coding and common character sets
- Soft music -js find the number of times that character appears in the string - Feng Hao's blog
- (lightoj - 1349) Aladdin and the optimal invitation (greed)
- Detailed explanation of FLV format
- 提交Spark应用的若干问题记录(sparklauncher with cluster deploy mode)
- 875. 爱吃香蕉的珂珂 - 力扣(LeetCode)
- Submit several problem records of spark application (sparklauncher with cluster deploy mode)
- Cmake Express
- Market trend report, technical innovation and market forecast of tabletop dishwashers in China
猜你喜欢
第5章 消费者组详解

Log statistics (double pointer)
【锟斤拷】的故事:谈谈汉字编码和常用字符集
SQL快速入门
![Solve the problem of intel12 generation core CPU [small core full, large core onlookers] (win11)](/img/92/9465a6c9f1ab88c4851a47fabe750c.jpg)
Solve the problem of intel12 generation core CPU [small core full, large core onlookers] (win11)
Sublime text code formatting operation
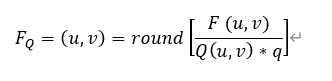
视频压缩编码和音频压缩编码基本原理
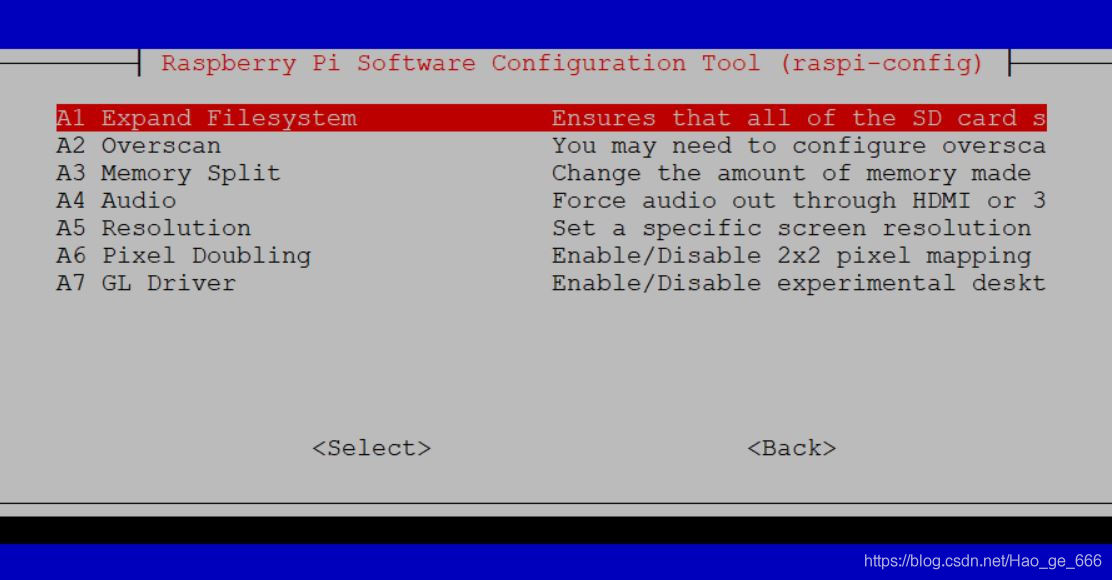
Raspberry pie 4B installation opencv3.4.0
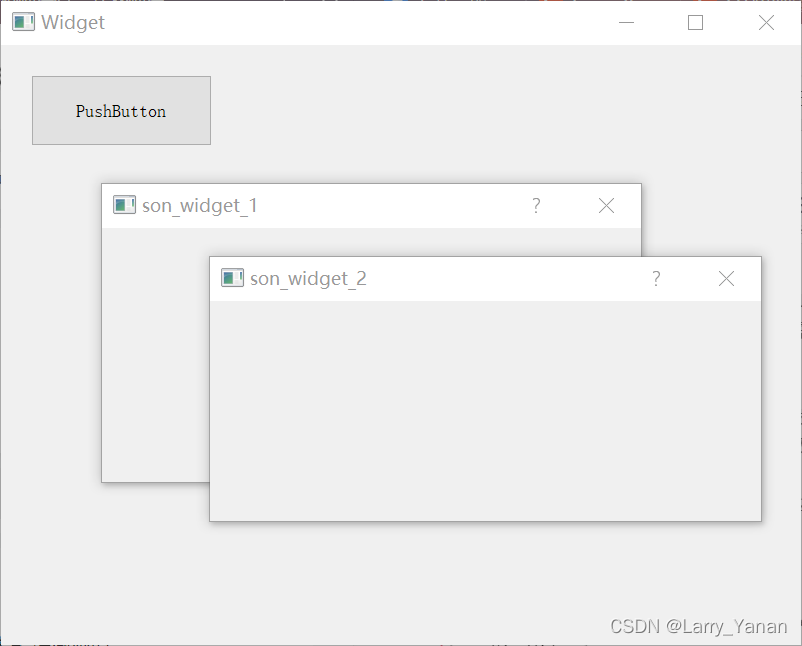
QT realizes window topping, topping state switching, and multi window topping priority relationship
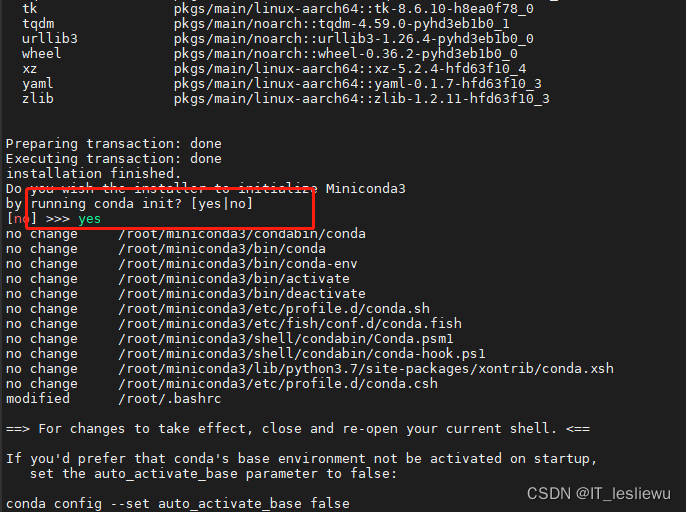
Raspberry pie 4b64 bit system installation miniconda (it took a few days to finally solve it)
随机推荐
Simple records of business system migration from Oracle to opengauss database
Gridhome, a static site generator that novices must know
音视频开发面试题
Codeforces round 797 (Div. 3) no f
图像处理一百题(11-20)
第6章 Rebalance详解
Codeforces Round #802(Div. 2)A~D
ByteDance new programmer's growth secret: those glittering treasures mentors
第6章 DataNode
使用jq实现全选 反选 和全不选-冯浩的博客
Browser print margin, default / borderless, full 1 page A4
解决Intel12代酷睿CPU单线程只给小核运行的问题
875. 爱吃香蕉的珂珂 - 力扣(LeetCode)
Chapter III principles of MapReduce framework
Acwing: Game 58 of the week
FLV格式详解
Cmake Express
【锟斤拷】的故事:谈谈汉字编码和常用字符集
Educational Codeforces Round 122 (Rated for Div. 2)
Detailed explanation of FLV format