当前位置:网站首页>SDNU_ACM_ICPC_2022_Summer_Practice(1~2)
SDNU_ACM_ICPC_2022_Summer_Practice(1~2)
2022-07-07 22:48:00 【_dawn°】
目录
P8321 『JROI-4』沈阳大街 2(DP,思维,逆元)
P8346 「Wdoi-6」最澄澈的空与海(拓扑排序)

思路:因为条件是完美匹配恰好为1,那我们首先分类讨论:1、大于2时,此时我们可以多画几个图试试,一定是每个点的度都大于等于2,这个很好判断;2、等于1时,像样例的那样,我们发现满足仅有一个完美匹配时一定存在度为1的点;3、不存在,我们可以画一个图,像情况2一样,也一定存在度为1的点,例如:
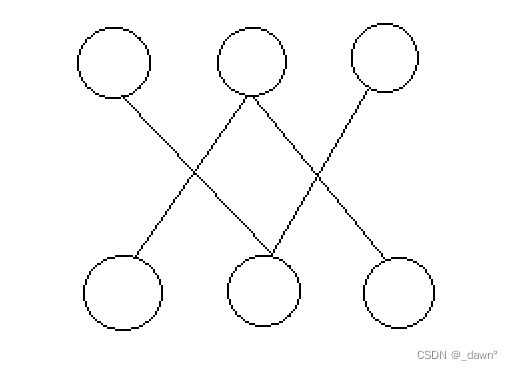
对于三种情况,第一种情况我们可以直接统计每个点的度;第二三种情况我们可以采用拓扑排序区分,计算入队出队的点数,判断是否等于2*n即可。
AC Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=1e6+5;
int t,n,m;
int cnt[N<<1],del[N<<1];
std::vector<int>vec[N<<1];
bool check(){
std::queue<int>q;
int cntt=0;
for(int i=1;i<2*n;i++){
if(cnt[i]==1) q.push(i);
}
while(!q.empty()){
int now=q.front(),nex=0;
q.pop();
if(del[now]) continue;
del[now]=1,cntt++;
for(int i=0;i<vec[now].size();i++){
if(del[vec[now][i]]) continue;
nex=vec[now][i];
break;
}
del[nex]=1,cntt++;
for(int i=0;i<vec[nex].size();i++){
if(!del[vec[nex][i]]){
--cnt[vec[nex][i]];
if(cnt[vec[nex][i]]==1) q.push(vec[nex][i]);
}
}
}
if(cntt!=n*2) return false;
return true;
}
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>t;
while(t--){
std::cin>>n>>m;
for(int i=0;i<=n*2+3;i++){
vec[i].clear();
}
memset(cnt,0,sizeof(cnt));
memset(del,0,sizeof(del));
for(int i=1;i<=m;i++){
int u,v;
std::cin>>u>>v;
v+=n;
cnt[u]++,cnt[v]++;
vec[u].push_back(v);
vec[v].push_back(u);
}
bool flag=true;
for(int i=1;i<=(n<<1);i++){
if(cnt[i]<2){
flag=false;
break;
}
}
if(flag){
std::cout<<"Merry"<<'\n';
continue;
}
std::cout<<(check()?"Renko":"Merry")<<'\n';
}
return 0;
}
P8347 「Wdoi-6」另一侧的月(博弈)

思路:结论型博弈问题,可以先从简单的情况开始:一个点时,先手必胜;两个点时,后手必胜;三个点时,排成一条线则先手必胜,菊花图则后手必胜。分析这些简单的样例,发现结论:若存在偶数度的点,则先手必胜,反之则后手必胜,以下证明:
我们可以设N态为全为奇数度,P态为存在偶数度,根据博弈论,我们只要证明局势状态是P和N交替出现即可。首先我们能够发现题目中的操作就是选一条边切断,后继状态为切断后其中一棵子树。对于 N 态,我们假设切断的边为连接u和v的边,则由于原树中u,v的度数均为奇数,因此切断后u,v的度数均为偶数,此时无论选择哪边的子树都存在一个点度数为偶数;对于P态,由于至多只有有限个点度数为偶数,因此任意钦定一个根后必定有一棵子树中只有根节点的度数是偶数,此时选择这一棵子树作为后继状态,即为 N 态。
AC Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=1e5+5;
int t,n,u,v;
int cnt[N];
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>t;
while(t--){
std::cin>>n;
memset(cnt,0,sizeof(cnt));
for(int i=1;i<n;i++){
std::cin>>u>>v;
cnt[u]++,cnt[v]++;
}
bool flag=false;
for(int i=1;i<=n;i++){
if(!(cnt[i]&1)){
flag=true;
break;
}
}
std::cout<<(flag?"Hifuu":"Luna")<<'\n';
}
return 0;
}
P8348 「Wdoi-6」未知之花魅知之旅(思维,数学)

思路:首先特判给出的四个数小于k的情况。要满足题目要求,我们直接用某种方式构造数组使得a0,a1变成x,y是不可取的,因为数据范围太大,所以我们可以考虑用某种构造方式使得这两对数构造出相同的一对数。满足条件其实很简单,但是如果一路加的话,最后得到的值太大不好处理,所以可以使用加法和减法,这样一组数据是满足条件的:x,y,x+y,x,y,x+y......我们可以发现一次加法可以被两次减法抵消,对答案没有影响,所以我们可以一直做减法,直到没法继续减了为止,判断两对数的对应数是否相等即可。注意减法要用乘除快速处理,直接加减会TLE。
AC Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=1e5+5;
int t,a,b,x,y,k;
void work(int &x,int &y){
while(1){
if(x<y){
int now=(y-k)/x;
if(!now) break;
y-=now*x;
if(now&1) std::swap(x,y);
}
else if(x>y){
int now=(x-k)/y;
if(!now) break;
x-=now*y;
if(now&1) std::swap(x,y);
}
else break;
}
}
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>t;
while(t--){
std::cin>>a>>b>>x>>y>>k;
if(k>a||k>b||k>x||k>y){
std::cout<<"no"<<'\n';
continue;
}
work(a,b);
work(x,y);
if(a!=x||b!=y) std::cout<<"no"<<'\n';
else std::cout<<"yes"<<'\n';
}
return 0;
}
P8319 『JROI-4』分数(数学,规律)

思路:虽然赛时做出来了但是还是写一下。题面一开始理解有误,我觉得应该加上一句,约分约到最简,约分不算操作次数。自己写几个样例可以知道,约分次数最少时,操作次数越多,对于一个数,显然当它是质数时答案等于它自己,这样这个题就转化成了求小于等于给出数的最大质数。线筛筛一下,二分查找答案即可,当然也可以直接预处理,O(1)查询。
AC Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=2e6+5;
int t,n,tot;
int prime[N];
bool mark[N];
void oula(){
for(int i=2;i<=N-3;++i){
if(!mark[i])
prime[++tot]=i;
for(int j=1;j<=tot;++j){
if(i*prime[j]>N) break;
mark[i*prime[j]]=1;
if(i%prime[j]==0) break;
}
}
}
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
oula();
std::cin>>t;
while(t--){
std::cin>>n;
if(n==1){
std::cout<<1<<'\n';
continue;
}
int pos=std::lower_bound(prime+1,prime+1+tot,n)-prime;
if(prime[pos]!=n)
pos--;
std::cout<<prime[pos]<<'\n';
}
return 0;
}P8320 『JROI-4』Sunset(二分)

思路:注意理解d数组的含义,所以可以发现d数组是有序的,最后一个一定是数组中最大的数。操作2是将a中的这个数改为0,一并修改d数组的值,这样很容易想到,修改一个大数的值为0后,再找到的就是小于这个数的元素了。做法就是找到每一个数d数组值不同的地方,因为这个位置一定是a数组中这个数的位置。再看数据范围,5500次询问,500个数,每个数最多询问11次,需要采用二分查找。
AC Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=505;
int t,n;
int a[N];
inline int getmax(){
std::cout<<"? 1 "<<n<<std::endl;
std::cout<<std::flush;
int g;scanf("%d",&g);
int l=1,r=n,mid,ans,tmp;
while (l<=r){
mid=(l+r)>>1;
std::cout<<"? 1 "<<mid<<std::endl;
std::cout<<std::flush;
std::cin>>tmp;
if (tmp==g){
ans=mid;
r=mid-1;
}
else l=mid+1;
}
return ans;
}
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>t;
while (t--){
std::cin>>n;
memset(a,0,sizeof(a));
for(int i=n;i>1;i--){
int k=getmax();
a[k]=i;
std::cout<<"? 2 "<<k<<std::endl;
std::cout<<std::flush;
}
for(int i=1;i<=n;i++){
if (a[i]==0) a[i]=1;
}
std::cout<<"!";
for(int i=1;i<=n;i++)
std::cout<<' '<<a[i];
std::cout<<std::endl;
std::cout<<std::flush;
}
return 0;
}P8321 『JROI-4』沈阳大街 2(DP,思维,逆元)

思路:看上去要求的东西很吓人,但是我们可以提取其中的模型。我们可以看做将a数组和b数组合起来,a数组的数标为红色,b数组的数标位蓝色,降序排列后选择n对红蓝配对中后者的和(看的洛谷大佬的解析,好好理解一下,确实很妙)考虑DP解决,假设f[i][j]表示c[1,i]当中配对了j个的方案数。
转移方程:f[i][j]=f[i−1][j−1]×c[i]×(tmp−(j−1))+f[i−1][j]
这里tmp是c[1,i-1]中与c[i]不同色的数的个数,在DP过程前预处理cnt数组,是计算前i个数中属于红蓝数组的元素个数。
对于最后的答案,因为有个1/n!,这里有取模运算,所以要用费马小定理求逆元得到答案。
AC Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=998244353;
const int N=5e3+5;
ll n,a,b;
ll f[N<<1][N];
int cnt[2][N<<1];
struct node{
ll val;
ll belong;
bool operator <(const node &a) const{
return val>a.val;
}
} e[N<<1];
ll pmod(ll a,ll b){
ll res=1;
while(b){
if(b&1) res=res*a%mod;
b>>=1;
a=a*a%mod;
}
return res;
}
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>n;
for(int i=1;i<=n;i++){
std::cin>>a;
e[i].val=a,e[i].belong=0;
}
for(int i=1;i<=n;i++){
std::cin>>b;
e[i+n].val=b,e[i+n].belong=1;
}
std::sort(e+1,e+1+n*2);
for(int i=1;i<=2*n;i++){
cnt[0][i]=cnt[0][i-1];
cnt[1][i]=cnt[1][i-1];
cnt[e[i].belong][i]++;
}
f[0][0]=1;
for(ll i=1;i<=2*n;i++){
ll tmp=cnt[!e[i].belong][i];
f[i][0]=1;
for(ll j=1;j<=std::min(n,i);j++){
if(j<=tmp)
f[i][j]=f[i-1][j-1]*e[i].val%mod*(tmp-(j-1))%mod;
f[i][j]=(f[i-1][j]+f[i][j])%mod;
}
}
ll res=1;
for(int i=1;i<=n;i++){
res=res*i%mod;
}
std::cout<<pmod(res,mod-2)*f[2*n][n]%mod;
return 0;
}os:第二次训练赛好像是某场洛谷的月赛,,看了看后面俩题,这是什么数论场啊,补不动了,卷积啥的还没接触过嘞(
若有错误请指教,谢谢!
边栏推荐
- 爬虫实战(八):爬表情包
- An error is reported during the process of setting up ADG. Rman-03009 ora-03113
- 51 communicates with the Bluetooth module, and 51 drives the Bluetooth app to light up
- Kubernetes Static Pod (静态Pod)
- If an exception is thrown in the constructor, the best way is to prevent memory leakage?
- 3年经验,面试测试岗20K都拿不到了吗?这么坑?
- Operating system principle --- summary of interview knowledge points
- RPA cloud computer, let RPA out of the box with unlimited computing power?
- Emotional post station 010: things that contemporary college students should understand
- 3 years of experience, can't you get 20K for the interview and test post? Such a hole?
猜你喜欢

51 communicates with the Bluetooth module, and 51 drives the Bluetooth app to light up
Qt不同类之间建立信号槽,并传递参数
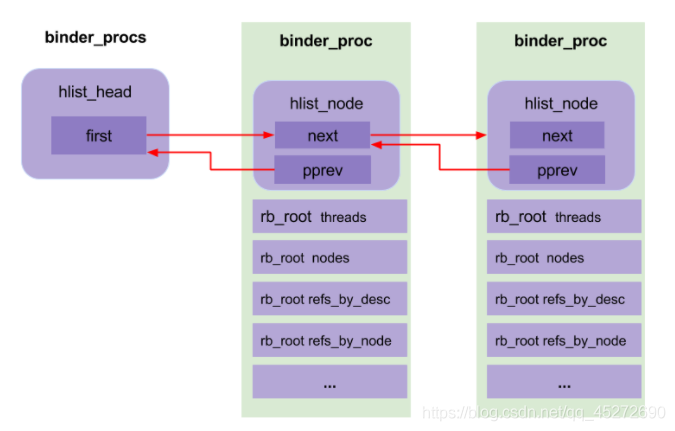
Binder核心API

51与蓝牙模块通讯,51驱动蓝牙APP点灯
某马旅游网站开发(对servlet的优化)
![[basis of recommendation system] sampling and construction of positive and negative samples](/img/4b/753a61b583cf38826b597fd31e5d20.png)
[basis of recommendation system] sampling and construction of positive and negative samples
赞!idea 如何单窗口打开多个项目?
【GO记录】从零开始GO语言——用GO语言做一个示波器(一)GO语言基础
腾讯安全发布《BOT管理白皮书》|解读BOT攻击,探索防护之道

去了字节跳动,才知道年薪 40w 的测试工程师有这么多?
随机推荐
ReentrantLock 公平锁源码 第0篇
Scrapy framework
[programming problem] [scratch Level 2] December 2019 flying birds
[question de programmation] [scratch niveau 2] oiseaux volants en décembre 2019
[研发人员必备]paddle 如何制作自己的数据集,并显示。
Jouer sonar
他们齐聚 2022 ECUG Con,只为「中国技术力量」
Kubernetes Static Pod (静态Pod)
如果在构造函数中抛出异常,最好的做法是防止内存泄漏?
Linkedblockingqueue source code analysis - add and delete
从Starfish OS持续对SFO的通缩消耗,长远看SFO的价值
Deep dive kotlin collaboration (the end of 23): sharedflow and stateflow
智慧监管入场,美团等互联网服务平台何去何从
How to learn a new technology (programming language)
什么是负载均衡?DNS如何实现负载均衡?
华为交换机S5735S-L24T4S-QA2无法telnet远程访问
Solution to prompt configure: error: curses library not found when configuring and installing crosstool ng tool
【愚公系列】2022年7月 Go教学课程 006-自动推导类型和输入输出
redis你到底懂不懂之list
丸子官网小程序配置教程来了(附详细步骤)