论文笔记: 图神经网络 GAT

摘要: 分享对论文的理解. 原文见 Petar Velickovic, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, Yoshua Bengio, Graph attention networks, ICLR 2018, 1–12. 可以在 ArXiv: 1710.10903v3 下载. 完全难以估计影响力有多大!

1. 论文贡献

• 克服图卷积已有方法的缺点.
• 不需要耗时的矩阵运算 (如求逆).
• 不需要预知图的结构.
• 适用于归纳与演绎问题.

2. 基础思想

利用邻居的信息, 将图中节点原始属性映射到一个新的空间, 以支持后面的学习任务.
这个思想可能是不同图神经网络所共有的.

3. 方案

Table 1. Notations.

符号	含义	备注
$N$	节点数
$F$	原始特征数
$F^{\prime }$	原始特征数	例中为 4
$\mathbf{h}$	结点特征集合	$\{{\overrightarrow{h}}_1，\dots ,{\overrightarrow{h}}_N\}$
${\overrightarrow{h}}_i$	第 $i$ 个节点的特征	属于空间 ${\mathbb{R}}^F$
${\mathbf{h}}^{\prime }$	结点新的特征集合	$\{{\overrightarrow{h}}_1^{\prime }，\dots ,{\overrightarrow{h}}_N^{\prime }\}$
${\overrightarrow{h}}_i^{\prime }$	第 $i$ 个节点的新特征	属于空间 ${\mathbb{R}}^{F^{\prime }}$
$\mathbf{W}$	特征映射矩阵	属于 ${\mathbb{R}}^{F\times F^{\prime }}$, 所有节点共享
${\mathcal{N}}_i$	节点 $i$ 的邻居集合	包括 $i$ 自己, 例中基数为 6
$\overrightarrow{\mathbf{a}}$	特征权值向量	属于 ${\mathbb{R}}^{2F^{\prime }}$, 所有节点共享, 对应于单层网络
${\alpha }_{ij}$	节点 $j$ 对 $i$ 的影响	所有邻居节点的影响之和为 1
${\overrightarrow{\alpha }}_{ij}$	节点 $j$ 对 $i$ 的影响向量	长度为 $K$, 对应于多头

将节点特征映射到新空间, 利用注意力机制 $a$ 计算节点间的关系
$$e_{ij}=a(\mathbf{W}{\overrightarrow{h}}_i,\mathbf{W}{\overrightarrow{h}}_j)\text{\hspace{1em}(1)}$$
这里仅当 $j$ 是 $i$ 在网络上的邻居时, 才计算 $e_{ij}$.
将它进行 softmax, 使得节点 $i$ 对应的权值和为 1.
$${\alpha }_{ij}={\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}}_j(e_{ij})=\frac{\exp (e_{ij})}{{\sum }_{k\in {\mathcal{N}}_i}\exp (e_{ik})}\text{\hspace{1em}(2)}$$
由于 $a$ 将长度为 $2F^{\prime }$ 的列向量转换为一个标量, 可以将其写作一个相同长度的行向量 ${\overrightarrow{\mathbf{a}}}^{\mathrm{T}}$. 再加上一个激活函数, 它就可以用单层的神经网络实现.

$${\alpha }_{ij}=\frac{\exp (\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{y}\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{u}({\overrightarrow{\mathbf{a}}}^{\mathrm{T}}[\mathbf{W}{\overrightarrow{h}}_i\Vert \mathbf{W}{\overrightarrow{h}}_j]))}{{\sum }_{k\in {\mathcal{N}}_i}\exp (\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{y}\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{u}({\overrightarrow{\mathbf{a}}}^{\mathrm{T}}[\mathbf{W}{\overrightarrow{h}}_i\Vert \mathbf{W}{\overrightarrow{h}}_k]))}\text{\hspace{1em}(2)}$$

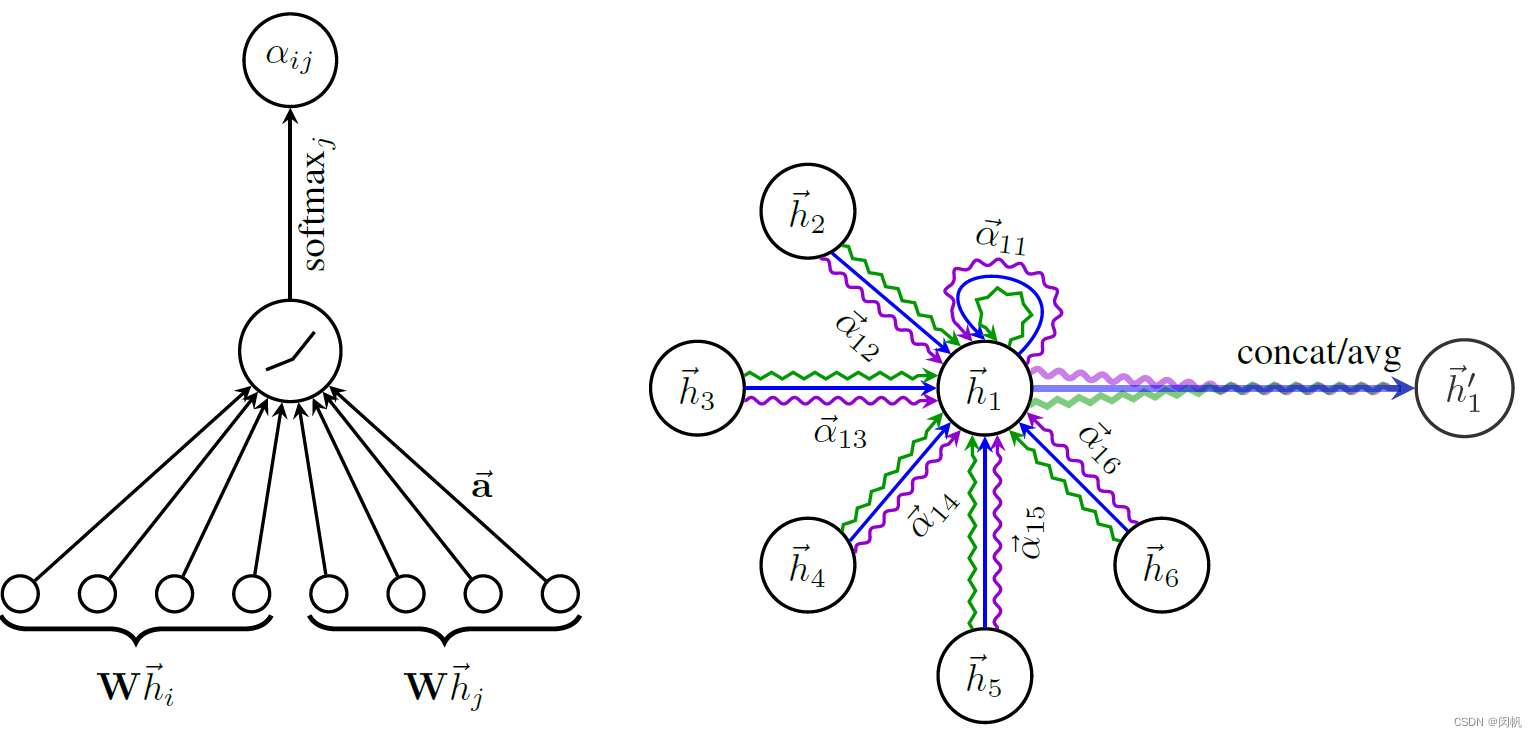
图 1. GAT 核心方案. 左: $F^{\prime }=4$ 的时候, 从 $\mathbf{W}$ 映射到的新空间为 4 维. 相应的 $2F^{\prime }=8$ 维. 向量 $\overrightarrow{\mathbf{a}}$ 由所有的节点共享. 右: $K=3$ 个头.

3.1 方案一: 单头

$${\overrightarrow{h}}_i^{\prime }=\sigma \left(\sum _{j\in i}{\alpha }_{ij}\mathbf{W}{\overrightarrow{h}}_j\right)\text{\hspace{1em}(4)}$$
所有邻居节点先映射到新空间 (如 4 维), 然后根据其影响力加权求和, 并用 sigmoid 等非线性激活函数, 最终获得的还是 4 维向量.

3.2 方案二: 多头连接

$${\overrightarrow{h}}_i^{\prime }={\Vert }_{k=1}^K\sigma \left(\sum _{j\in {\mathcal{N}}_i}{\alpha }_{ij}^k{\mathbf{W}}^k{\overrightarrow{h}}_j\right)\text{\hspace{1em}(5)}$$
$K$ 个头分别获得相应的新向量, 图 1 右展示了 3 个头, 因此最后的向量为 $3\times 4=12$ 维.

3.3 方案三: 多头平均

$${\overrightarrow{h}}_i^{\prime }=\sigma \left(\frac{1}{K}\sum _{k=1}^K\sum _{j\in {\mathcal{N}}_i}{\alpha }_{ij}^k{\mathbf{W}}^k{\overrightarrow{h}}_j\right)\text{\hspace{1em}(5)}$$
仅仅是平均值, 最后的向量为 $4$ 维.

4. 疑问

• 问题: 这里的 $\mathbf{W}$ 与 $\overrightarrow{\mathbf{a}}$ 如何学习?
  猜测: 可以从相关工作, 即图神经网络里面获得必要的知识. 这篇论文只是想描述不一样的核心技术.
  如果将这个网络的输出作为其它网络的输入 (最终输出为类标签等), 有可能就可以进行相应学习.
  唐文韬的解释: 本质上相当于矩阵相乘 (线性回归)，从论文代码里可以看出:在训练阶段，输入的是整个训练集 (特征矩阵和样本的邻接矩阵)，通过 $\mathbf{W}$ 和 $\overrightarrow{\mathbf{a}}$ 得到训练集的预测标签 (先得到每个样本对于所有样本的自注意力权重，再根据邻接矩阵进行 mask，再归一化作为一层自注意力的权重), 然后进行 loss 的计算和传播。

• 问题: 为什么计算影响力的时候使用 LeakyReLU, 而计算最终特征向量的时候使用 sigmoid?
  强行解释: 前者只是与后者区别开 (非必要), 后者是改变线性 (有必要).
  唐文韬的解释: 计算影响力使用 LeakyReLU: 更多地关注与目标结点更加正相关的邻居结点。
  最终特征向量使用 sigmoid 应该是为了防止数值过大，影响下一层的学习，因为自注意力机制较为不稳定（从我之前的实验中看出），对数值的范围和稠密性要求较高（范围小:0-1之类，较为稠密）。
  此外，在 GAT 论文内给出的源代码中可以看出, 作者对所有数据集都仅使用了两层自注意力网络, 并且 dropout 都设为0.5-0.8, 可见其较容易过拟合。

5. 小结

• 利用 $\mathbf{W}$ 线性映射到新空间.
• 利用 $\overrightarrow{\mathbf{a}}$ 计算各邻居的影响力 ${\alpha }_{ij}$. $\overrightarrow{\mathbf{a}}$ 仅针对相应属性, 而不受邻居编号影响. ${\alpha }_{ij}$ 的计算涉及 LeakyReLU 激活函数的使用.
• 利用多头增加稳定性.
• 求均值、使用非线性函数激活都不会改变向量的维度.