当前位置:网站首页>[daily question] 729 My schedule I
[daily question] 729 My schedule I
2022-07-06 06:51:00 【Wang Liuliu's it daily】
729. My schedule I

Reference resources : The blog post written by the boss in the effort to explain the topic ----- Line tree details 「 Summary level collation 」
Line tree series :
The segment tree solves 「 Interval and 」 The problem of , And the 「 Section 」 Will be modified .
Take a simple one , about nums = [1, 2, 3, 4, 5].
If we need to sum a certain interval many times , Did you first think of using 「 The prefix and 」.
The detailed introduction of prefix and can be seen Prefixes and arrays
nums = [1, 2, 3, 4, 5] The corresponding segment tree is as follows :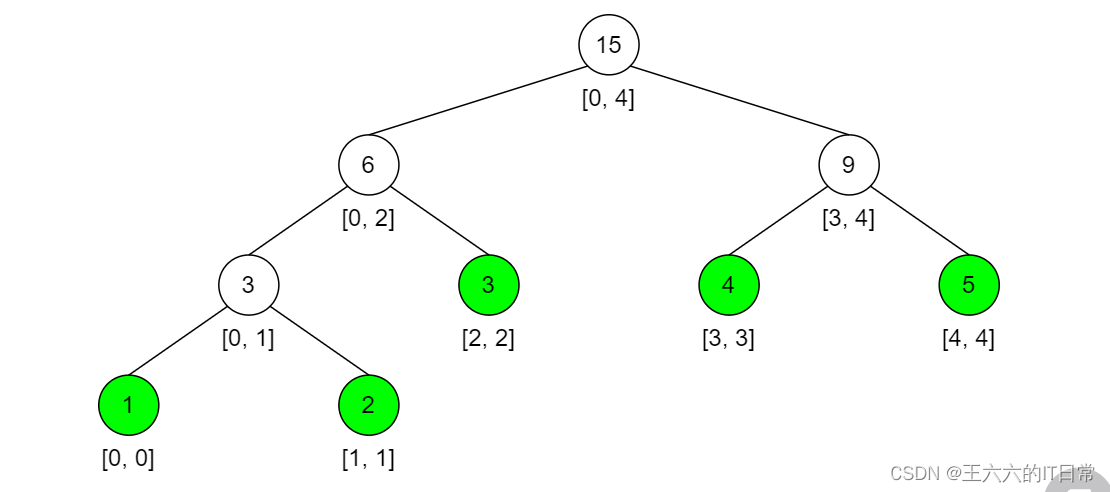
Each node represents an interval , And the value of the node is the sum of the interval .
- Sum of numbers 「 The sum of the total figures = The sum of the numbers in the left range + The sum of the numbers in the right range 」
- The greatest common factor (GCD)「 total GCD = gcd( Left interval GCD, The right range GCD)」
- Maximum 「 Total maximum = max( The maximum value of the left range , Maximum value in the right range )」
Data structure of segment tree
We can use arrays to represent a segment tree , Suppose the root node is i, Then the node of the left child is 2 * i, The node of the right child is 2 * i + 1 ( Premise :i from 1 Start )
We can use a linked list to represent a segment tree , The data structure of its nodes is as follows :
class Node {
// Left and right child nodes
Node left, right;
// Current node value
int val;
}
Prefer to use linked lists , Because it saves memory , The following implementations are based on linked lists .
Establishment of line segment tree
If a specific range is given in the title , We build a segment tree according to this range .
public void buildTree(Node node, int start, int end) {
// To the leaf node
if (start == end) {
node.val = arr[start];
return ;
}
int mid = (start + end) >> 1;
buildTree(node.left, start, mid);
buildTree(node.right, mid + 1, end);
// Update up
pushUp(node);
}
// Update up
private void pushUp(Node node) {
node.val = node.left.val + node.right.val;
}
But a lot of times , No specific scope is given in the title , Only the value range of data , It's usually big , So we often use 「 Dynamic opening point 」.
「 Dynamic opening point 」 Usually in 「 to update 」 or 「 Inquire about 」 Dynamically establish nodes when , See the following update and query operations for details .
Complete template of segment tree
Be careful : The following template is based on 「 Interval and 」 And the interval 「 Addition and subtraction 」 Update operation for , And for 「 Dynamic opening point 」
/** * @Description: Line segment tree ( Dynamic opening point ) * @Author: LFool * @Date 2022/6/7 09:15 **/
public class SegmentTreeDynamic {
class Node {
Node left, right;
int val, add;
}
private int N = (int) 1e9;
private Node root = new Node();
public void update(Node node, int start, int end, int l, int r, int val) {
if (l <= start && end <= r) {
node.val += (end - start + 1) * val;
node.add += val;
return ;
}
int mid = (start + end) >> 1;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) update(node.left, start, mid, l, r, val);
if (r > mid) update(node.right, mid + 1, end, l, r, val);
pushUp(node);
}
public int query(Node node, int start, int end, int l, int r) {
if (l <= start && end <= r) return node.val;
int mid = (start + end) >> 1, ans = 0;
pushDown(node, mid - start + 1, end - mid);
if (l <= mid) ans += query(node.left, start, mid, l, r);
if (r > mid) ans += query(node.right, mid + 1, end, l, r);
return ans;
}
private void pushUp(Node node) {
node.val = node.left.val + node.right.val;
}
private void pushDown(Node node, int leftNum, int rightNum) {
if (node.left == null) node.left = new Node();
if (node.right == null) node.right = new Node();
if (node.add == 0) return ;
node.left.val += node.add * leftNum;
node.right.val += node.add * rightNum;
// The interval is 「 Addition and subtraction 」 Update operation for , You need to add up when pushing down the lazy flag , Cannot directly cover
node.left.add += node.add;
node.right.add += node.add;
node.add = 0;
}
}
class MyCalendar {
public MyCalendar() {
}
public boolean book(int start, int end) {
// First query whether the interval is 0
if (query(root, 0, N, start, end - 1) != 0) return false;
// Update the interval
update(root, 0, N, start, end - 1, 1);
return true;
}
// *************** Here is the template ***************
class Node {
// Left and right child nodes
Node left, right;
// Current node value , And the value of the lazy tag
int val, add;
}
private int N = (int) 1e9;
private Node root = new Node();
public void update(Node node, int start, int end, int l, int r, int val) {
if (l <= start && end <= r) {
node.val += val;
node.add += val;
return ;
}
pushDown(node);
int mid = (start + end) >> 1;
if (l <= mid) update(node.left, start, mid, l, r, val);
if (r > mid) update(node.right, mid + 1, end, l, r, val);
pushUp(node);
}
public int query(Node node, int start, int end, int l, int r) {
if (l <= start && end <= r) return node.val;
pushDown(node);
int mid = (start + end) >> 1, ans = 0;
if (l <= mid) ans = query(node.left, start, mid, l, r);
if (r > mid) ans = Math.max(ans, query(node.right, mid + 1, end, l, r));
return ans;
}
private void pushUp(Node node) {
// Each node stores the maximum value of the current interval
node.val = Math.max(node.left.val, node.right.val);
}
private void pushDown(Node node) {
if (node.left == null) node.left = new Node();
if (node.right == null) node.right = new Node();
if (node.add == 0) return ;
node.left.val += node.add;
node.right.val += node.add;
node.left.add += node.add;
node.right.add += node.add;
node.add = 0;
}
}
/** * Your MyCalendar object will be instantiated and called as such: * MyCalendar obj = new MyCalendar(); * boolean param_1 = obj.book(start,end); */
边栏推荐
- LeetCode - 152 乘积最大子数组
- 删除外部表源数据
- Data security -- 13 -- data security lifecycle management
- LeetCode每日一题(1997. First Day Where You Have Been in All the Rooms)
- 19.段页结合的实际内存管理
- Fedora/REHL 安装 semanage
- How much is the price for the seal of the certificate
- 从autojs到冰狐智能辅助的心里历程
- ML之shap:基于adult人口普查收入二分类预测数据集(预测年收入是否超过50k)利用Shap值对XGBoost模型实现可解释性案例之详细攻略
- [English] Grammar remodeling: the core framework of English Learning -- English rabbit learning notes (1)
猜你喜欢
Introduction and underlying analysis of regular expressions
After sharing the clone remote project, NPM install reports an error - CB () never called! This is an error with npm itself.
Leetcode daily question (971. flip binary tree to match preorder traversal)
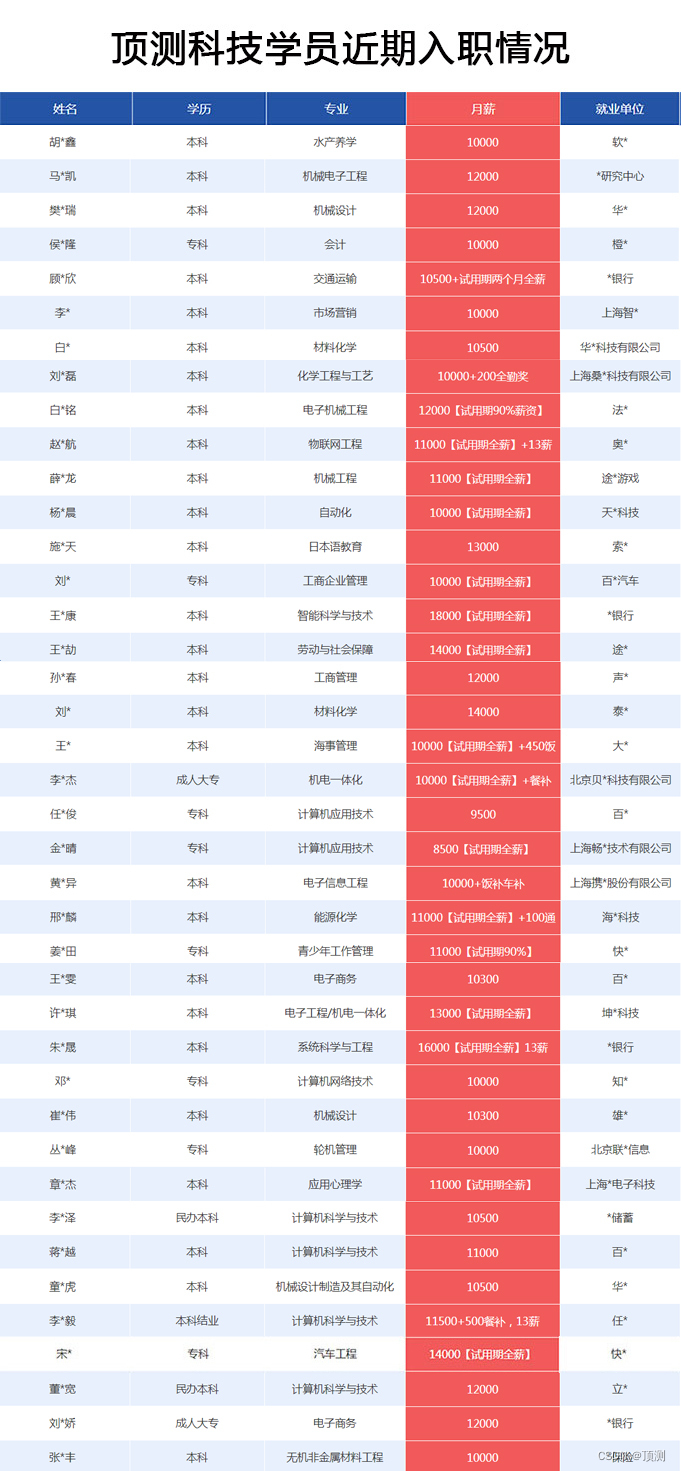
顶测分享:想转行,这些问题一定要考虑清楚!
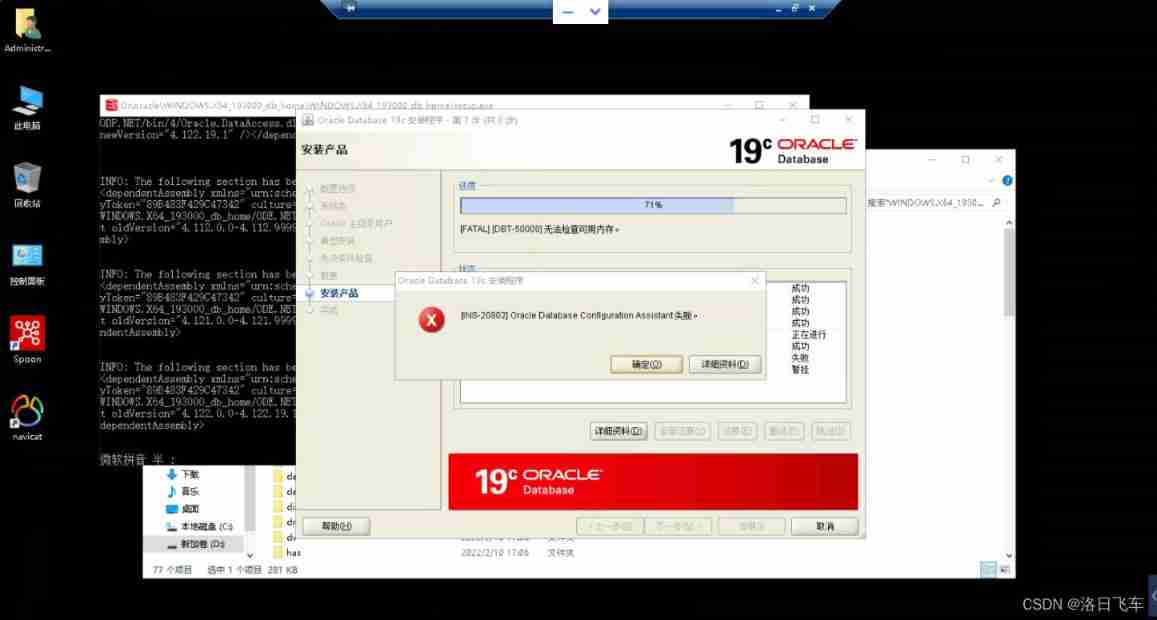
Windows Server 2016 standard installing Oracle

mysql的基础命令
When my colleague went to the bathroom, I helped my product sister easily complete the BI data product and got a milk tea reward

Cobalt strike feature modification
【刷题】怎么样才能正确的迎接面试?

Changes in the number of words in English papers translated into Chinese
随机推荐
The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
Automated test environment configuration
【Hot100】739. 每日温度
Fedora/REHL 安装 semanage
[brush questions] how can we correctly meet the interview?
Map of mL: Based on the adult census income two classification prediction data set (whether the predicted annual income exceeds 50K), use the map value to realize the interpretable case of xgboost mod
How to reconstruct the class explosion caused by m*n strategies?
Thesis abstract translation, multilingual pure human translation
The internationalization of domestic games is inseparable from professional translation companies
Day 246/300 SSH connection prompt "remote host identification has changed!"
利用快捷方式-LNK-上线CS
[ 英语 ] 语法重塑 之 动词分类 —— 英语兔学习笔记(2)
Leetcode daily question (1870. minimum speed to arrive on time)
SSO process analysis
MySQL5.72. MSI installation failed
机器人类专业不同层次院校课程差异性简述-ROS1/ROS2-
[advanced software testing step 1] basic knowledge of automated testing
钓鱼&文件名反转&office远程模板
Market segmentation of supermarket customers based on purchase behavior data (RFM model)
基于购买行为数据对超市顾客进行市场细分(RFM模型)