当前位置:网站首页>EOJ 2021.10 E. XOR tree
EOJ 2021.10 E. XOR tree
2022-07-05 05:31:00 【solemntee】
Method 1 : First open a big pile . then d f s dfs dfs Again , Build a persistent dictionary tree , And each point throws the XOR maximum of itself and its ancestors into the heap . loop k k k Time , Each time the maximum value is ejected from the heap , Suppose the ejected point has been ejected x x x Time , Search the dictionary tree for its number x + 1 x+1 x+1 Large XOR value , Then throw it into the pile . Time complexity O ( 30 n + k ( l o g n + 30 ) ) O(30n+k(logn+30)) O(30n+k(logn+30))
1. This problem also reflects a skill, that is, to do the first k Great value (k< 1 e 6 1e6 1e6) The common method is to maintain a priority queue, get the maximum value each time, and then update .
2. The problem is no x All nodes can be persistent. The dictionary tree represents from the root to x The point group on the node chain Chengdu dictionary tree . Although in this way and query x The dictionary tree corresponding to the subtree of the node is equivalent , But in fact, this method can save one of tree chain partition when dealing with tree chain problem log
#include<bits/stdc++.h>
using namespace std;
struct
{
int vis[2];
int num;
}trie[30000005];
int tot;
int root[5000005];
int insert(int x,int rt)
{
int Root=++tot;
int now=root[rt];
for(int i=30;i>=0;i--)
/// This is determined according to the scope , The first one here is (1>>30) That is to say 2^31
{
int ch=(x>>i)&1;
trie[tot]=trie[now];
trie[tot].vis[ch]=tot+1;
trie[tot].num++;
now=trie[now].vis[ch];
tot++;
}
trie[tot]=trie[now];
trie[tot].num++;
return Root;
/// The reason for this is that it is convenient to build a tree root[x]=insert(a[x],i-1);
}
int query(int x,int k,int rt)
/// Inquire about x stay root[rt] The root of the persistent dictionary tree is XOR k Big
{
int now=root[rt];
int ans=0;
for(int i=30;i>=0;i--)
{
int ch=(x>>i)&1;
if(trie[trie[now].vis[!ch]].num>=k)
{
now=trie[now].vis[!ch];
ans|=(1<<i);
}
else
{
k-=trie[trie[now].vis[!ch]].num;
now=trie[now].vis[ch];
}
}
return ans;
}
struct node
{
int val,id,now;
bool operator < (const node &ths)const
{
if(val!=ths.val)return val<ths.val;
if(now!=ths.now)return now<ths.now;
return id<ths.id;
}
};
int dep[1000005],fa[1000005],a[1000005];
vector<int>v[1000005];
priority_queue<node>q;
void dfs(int x,int pre)
{
if(pre!=0)
{
dep[x]=dep[pre]+1;
fa[x]=pre;
q.push({
query(a[x],1,fa[x]),x,1});
}
root[x]=insert(a[x],pre);
for(auto to:v[x])if(to!=pre)
{
dfs(to,x);
}
}
vector<int>ans;
int main()
{
int n,k;
scanf("%d%d",&n,&k);
for(int i=1;i<n;i++)
{
int tu,tv;
scanf("%d%d",&tu,&tv);
v[tu].push_back(tv);
v[tv].push_back(tu);
}
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
dfs(1,0);
for(int i=1;i<=k;i++)
{
node p=q.top();
q.pop();
ans.push_back(p.val);
if(p.now<dep[p.id])q.push({
query(a[p.id],p.now+1,fa[p.id]),p.id,p.now+1});
}
for(auto x:ans)printf("%d\n",x);
return 0;
}
Method 2 : First create a persistent dictionary tree , Then two points k Great value , Then traverse all the dictionary trees violently to get the answer .
边栏推荐
- 每日一题-无重复字符的最长子串
- Solon Logging 插件的添加器级别控制和日志器的级别控制
- Annotation and reflection
- [binary search] 69 Square root of X
- National teacher qualification examination in the first half of 2022
- [turn to] MySQL operation practice (III): table connection
- 对象的序列化
- 剑指 Offer 35.复杂链表的复制
- Gbase database helps the development of digital finance in the Bay Area
- Sword finger offer 53 - I. find the number I in the sorted array
猜你喜欢
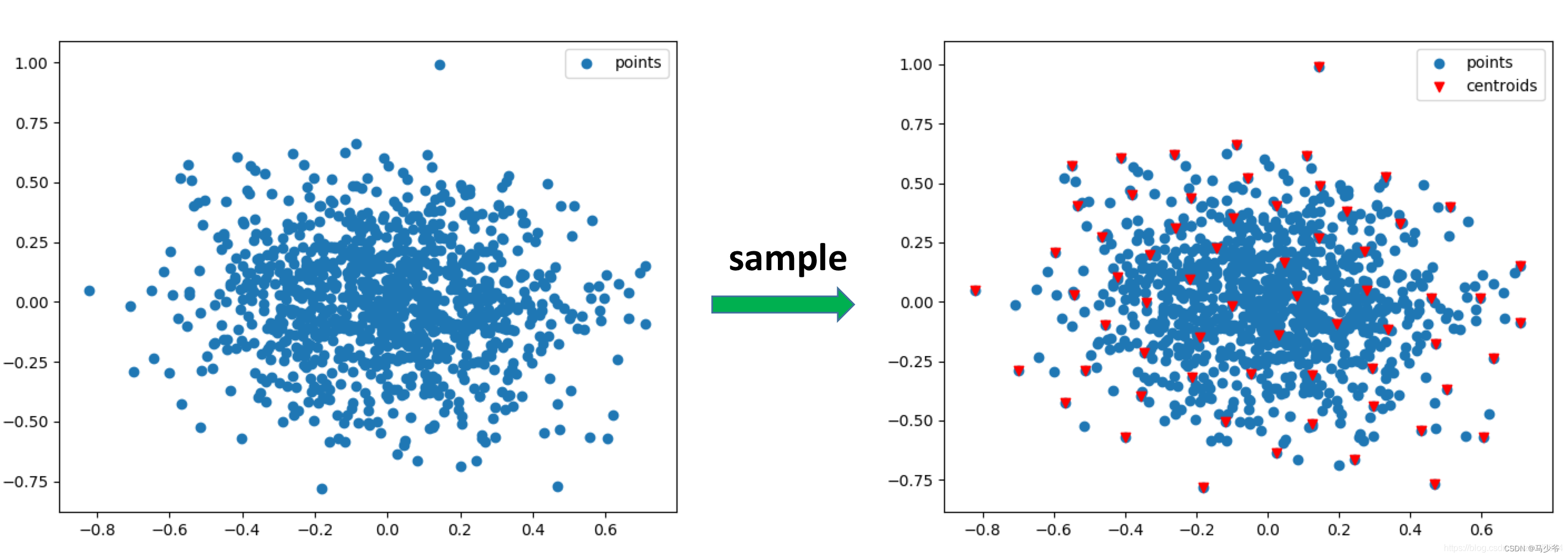
Pointnet++学习

对象的序列化
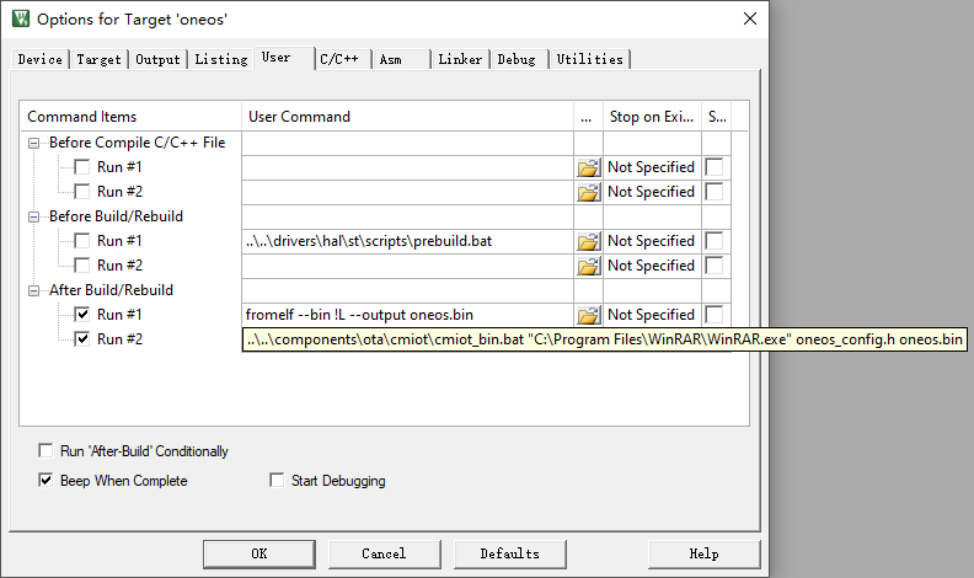
远程升级怕截胡?详解FOTA安全升级
![[turn to] MySQL operation practice (III): table connection](/img/70/20bf9b379ce58761bae9955982a158.png)
[turn to] MySQL operation practice (III): table connection
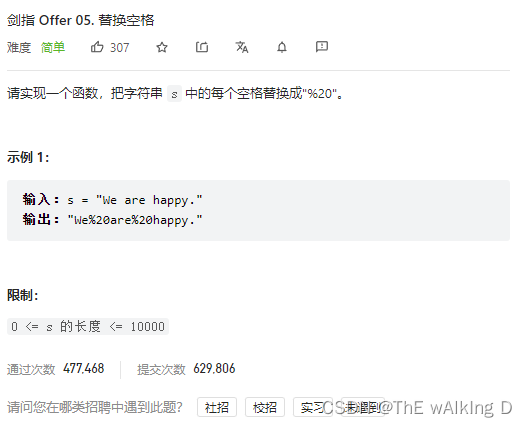
Sword finger offer 05 Replace spaces

Sword finger offer 05 Replace spaces
Using HashMap to realize simple cache

object serialization

Gbase database helps the development of digital finance in the Bay Area
Codeforces round 712 (Div. 2) d. 3-coloring (construction)
随机推荐
Support multi-mode polymorphic gbase 8C database continuous innovation and heavy upgrade
[turn to] MySQL operation practice (III): table connection
剑指 Offer 58 - II. 左旋转字符串
ALU逻辑运算单元
Zzulioj 1673: b: clever characters???
剑指 Offer 05. 替换空格
Haut OJ 1347: addition of choice -- high progress addition
Pointnet++学习
The number of enclaves
浅谈JVM(面试常考)
Sword finger offer 09 Implementing queues with two stacks
After setting up the database and website When you open the app for testing, it shows that the server is being maintained
Educational Codeforces Round 107 (Rated for Div. 2) E. Colorings and Dominoes
To be continued] [UE4 notes] L4 object editing
剑指 Offer 05. 替换空格
C language Essay 1
Sword finger offer 05 Replace spaces
kubeadm系列-02-kubelet的配置和启动
使用Room数据库报警告: Schema export directory is not provided to the annotation processor so we cannot expor
Sword finger offer 53 - ii Missing numbers from 0 to n-1
