当前位置:网站首页>Entropy method to calculate weight
Entropy method to calculate weight
2022-07-03 10:36:00 【Also far away】
One 、 Principle analysis of entropy method
1、 Select data
m Samples , common n Indicators , X i j X_{ij} Xij For the first i i i Of samples j j j The number of indicators , i = 1 , 2 , 3 , . . . m ; j = 1 , 2 , 3... n . i = 1 , 2 , 3 , . . . m ; j = 1 , 2 , 3... n. i=1,2,3,...m;j=1,2,3...n.
2、 Data standardization
When the measurement units and directions of various indicators are not unified , The data needs to be standardized , In order to avoid the meaningless logarithm when calculating entropy , You can add a real number of a smaller order to each value , Such as 0.001
(1) Positive correlation index
X ′ = X i j − M i n ( X i j ) M a x ( X i j ) − M i n ( X i j ) X'= \frac{X_{ij}- Min(X_{ij})}{Max(X_{ij})-Min(X_{ij})} X′=Max(Xij)−Min(Xij)Xij−Min(Xij)
(2) For negative indicators ( The smaller the better indicator )
X ′ = M a x ( X i j ) − X i j M a x ( X i j ) − M i n ( X i j ) X' = \frac{Max(X_{ij})-X_{ij}}{Max(X_{ij})-Min(X_{ij})} X′=Max(Xij)−Min(Xij)Max(Xij)−Xij
3、 Computation first j j j Item... Under this indicator i i i The proportion of samples in this index
Calculate the sample weight :
P i j = X i j ∑ i = 1 n X i j P_{ij} = \frac{X_{ij}}{\sum_{i=1}^nX_{ij}} Pij=∑i=1nXijXij
4、 Computation first j j j The entropy of this index
Calculate the index entropy :
e j = − 1 l n ( m ) ∗ ∑ i = 1 m ( P i j ∗ l n ( P i j ) ) e_j = -\frac{1}{ln(m)}*\sum_{i=1}^m(P_{ij}*ln(P_{ij})) ej=−ln(m)1∗i=1∑m(Pij∗ln(Pij))
, among m Is the number of samples .
5、 Computation first j j j The difference coefficient of each index
The information utility value of an index depends on the information entropy and 1 Difference between , Its value directly affects the size of the weight . The greater the value of information utility , The greater the importance of evaluation , The greater the weight .
d j = 1 − e j d_j=1-e_j dj=1−ej
6、 Calculate the weight of evaluation index
Use entropy method to estimate the weight of each index , Its essence is to use the difference coefficient of the index information to calculate , The higher the coefficient of difference , The greater the importance of evaluation ( Or the greater the weight , The greater the contribution to the evaluation results )
The first j jj The weight of each indicator :
w j = d j ∑ j = 1 m d j w_j=\frac{d_j}{\sum_{j=1}^md_j} wj=∑j=1mdjdj
7、 Calculate the comprehensive score of each sample
z i = ∑ j = 1 m w j x i j z_i=\sum_{j=1}^mw_jx_{ij} zi=j=1∑mwjxij
Two 、 Test cases
1、 This case data set is based on 2012 Mathematical modeling of national college students A Take some data of question as an example
| Sample No | Total amino acids | Aspartic acid | Threonine | Serine | Glutamate | Proline |
|---|---|---|---|---|---|---|
| Grape samples 1 | 2027.96 | 101.22 | 393.42 | 77.61 | 266.6 | 723.88 |
| Grape samples 2 | 2128.82 | 64.43 | 140.62 | 71.94 | 39.26 | 1560.97 |
| Grape samples 3 | 8397.28 | 108.07 | 222.35 | 173.08 | 67.54 | 7472.28 |
| Grape samples 4 | 2144.68 | 79.39 | 133.83 | 158.74 | 156.72 | 1182.23 |
| Grape samples 5 | 1844 | 52.28 | 145.09 | 164.05 | 102.43 | 816.08 |
| Grape samples 6 | 3434.17 | 68.01 | 102.42 | 75.78 | 80.6 | 2932.76 |
| Grape samples 7 | 2391.16 | 65.1 | 267.76 | 239.2 | 208.97 | 1096.28 |
| Grape samples 8 | 1950.76 | 72.09 | 345.87 | 44.23 | 176.02 | 962.01 |
2、 Complete code
import numpy as np
import pandas as pd
## Reading data
data=pd.read_csv('redputao.csv',encoding='utf-8',index_col=0)
indicator=data.columns.tolist() ## The number of indicators How many columns
project=data.index.tolist() ## Number of samples How many rows?
value=data.values
print(indicator)
print(project)
print(value)
## Define data standardization functions . In order to avoid the meaningless logarithm when calculating entropy , Translate the data , A constant is added to the standardized data 0.001
def std_data(value,flag):
for i in range(len(indicator)):
if flag[i]=='+':
value[:,i]=(value[:,i]-np.min(value[:,i],axis=0))/(np.max(value[:,i],axis=0)-np.min(value[:,i],axis=0))+0.01
elif flag[i]=='-':
value[:,i]=(np.max(value[:,i],axis=0)-value[:,i])/(np.max(value[:,i],axis=0)-np.min(value[:,i],axis=0))+0.01
return value
# Define entropy function 、 Entropy method calculates the weight of variables
def cal_weight(indicator, project, value):
p = np.array([[0.0 for i in range(len(indicator))] for i in range(len(project))])
# print(p)
for i in range(len(indicator)):
p[:, i] = value[:, i] / np.sum(value[:, i], axis=0)
e = -1 / np.log(len(project)) * sum(p * np.log(p)) # Calculate the entropy
g = 1 - e # Calculate the degree of consistency
w = g / sum(g) # Calculate weight
return w
# Indicates whether each indicator is a positive indicator or a negative indicator
flag=["+","+","+","+","+", "+","+","+","+","+",
"+","+","+","+","+", "+","+","+","+","+",
"+","+","+","+","+", "+","+","+","+","+",
"+","+","+","+","+", "+","+","+","+","+",
"+","+","+","+","+", "+","+","+","+","+",
"+","+","+","+"]
# Call the function to standardize the data , That is, add a positive or negative correlation flag for each data
std_value=std_data(value, flag)
# Call the function to calculate the weight
w = cal_weight(indicator, project, std_value)
w = pd.DataFrame(w, index=data.columns, columns=[' The weight '])
print(w)
# Call the function to get the score
score = np.dot(std_value, w).round(4) # The corresponding data is multiplied by the weight to get the score , Keep the result to four decimal places
score = pd.DataFrame(score, index=data.index, columns=[' Comprehensive score ']).sort_values(by=[' Comprehensive score '], ascending=False)
print(score)
3、 ... and 、 Test case running results
Running results 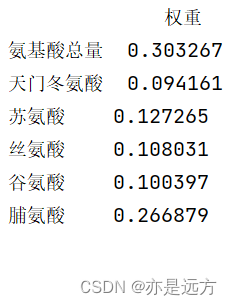

Four 、 Test forms
1、 Directly copy the above table to Excel
2、csv Download link Extraction code :1234
边栏推荐
- Multi-Task Feature Learning for Knowledge Graph Enhanced Recommendation
- Handwritten digit recognition: CNN alexnet
- Leetcode skimming ---202
- Softmax regression (pytorch)
- Timo background management system
- Anaconda installation package reported an error packagesnotfounderror: the following packages are not available from current channels:
- Ut2012 learning notes
- Leetcode刷题---44
- Several problems encountered in installing MySQL under MAC system
- Ind wks first week
猜你喜欢

一步教你溯源【钓鱼邮件】的IP地址

Adaptive Propagation Graph Convolutional Network
![[LZY learning notes dive into deep learning] 3.4 3.6 3.7 softmax principle and Implementation](/img/02/35e73a43c4ad26fee9ecf180593464.jpg)
[LZY learning notes dive into deep learning] 3.4 3.6 3.7 softmax principle and Implementation

Ut2013 learning notes
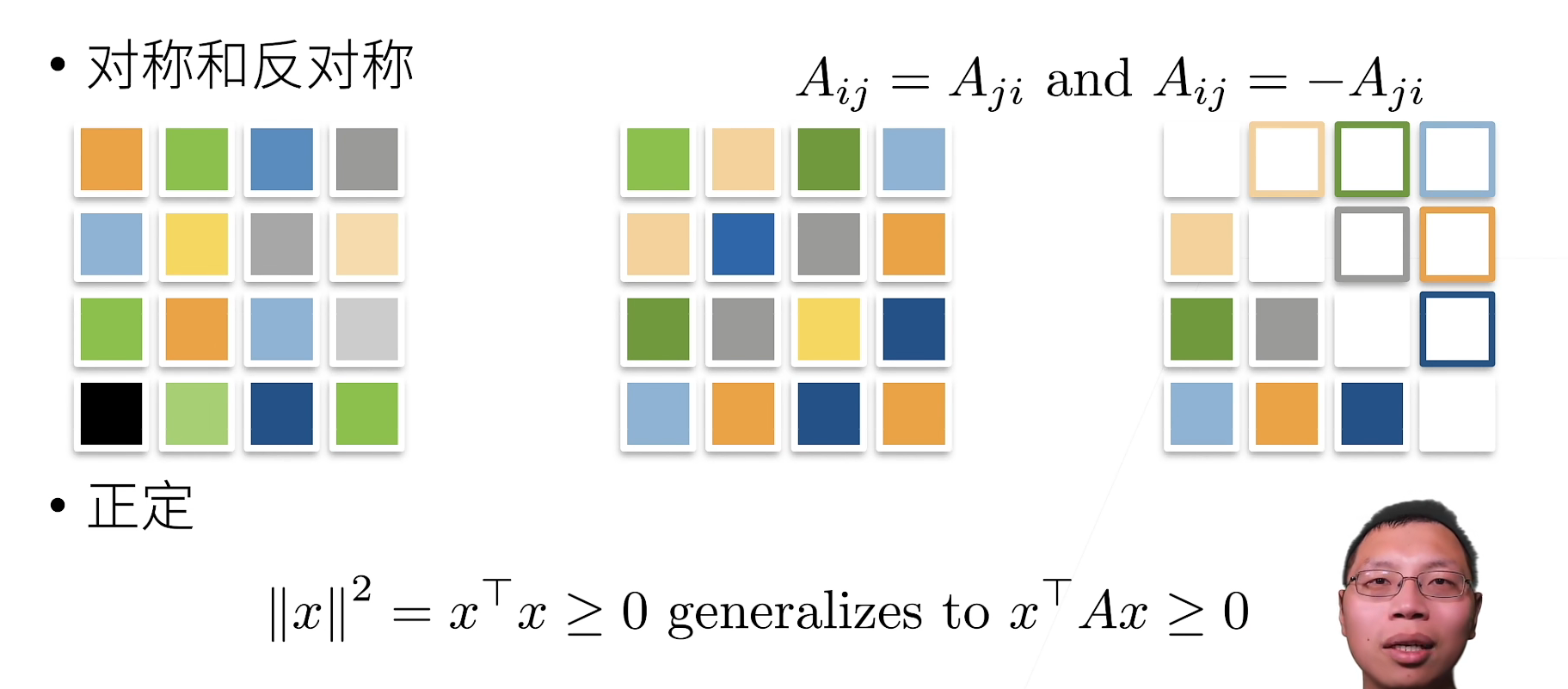
Introduction to deep learning linear algebra (pytorch)
深度学习入门之线性回归(PyTorch)

6、 Data definition language of MySQL (1)

Drop out (pytoch)

Are there any other high imitation projects
Tensorflow - tensorflow Foundation
随机推荐
Ut2016 learning notes
LeetCode - 715. Range module (TreeSet)*****
Leetcode skimming ---374
Policy Gradient Methods of Deep Reinforcement Learning (Part Two)
Leetcode刷题---374
Step 1: teach you to trace the IP address of [phishing email]
A super cool background permission management system
LeetCode - 900. RLE iterator
Leetcode skimming ---832
Codeup: word replacement
Jetson TX2 brush machine
Leetcode skimming ---44
Simple real-time gesture recognition based on OpenCV (including code)
20220531 Mathematics: Happy numbers
Drop out (pytoch)
Leetcode刷题---1
Ut2015 learning notes
Leetcode skimming ---852
C#项目-寝室管理系统(1)
2018 y7000 upgrade hard disk + migrate and upgrade black apple