[technical school] spatial accuracy of binocular stereo vision system: accurate quantitative analysis

In previous articles 【 Technical genre 】 Teach you to improve the accuracy of binocular stereo vision system ！ in , Bloggers made a more specific analysis about the accuracy of stereo vision system , But on the whole, it is qualitative , This article once again makes a quantitative analysis of accuracy , After all, accuracy is always the first factor in most scenes , Quantitative analysis is more conducive to system design and accuracy optimization . Hope to finish this article , Readers can further understand the determinants of accuracy and their respective scales of influence on accuracy , And be able to answer the following three questions ：

1. The accuracy of binocular stereo vision system depends on those factors ？
2. Do all factors have the same degree of determination of accuracy ？
3. X/Y/Z Is the accuracy of the three directions the same ？ If it's not the same , Which direction has better accuracy ？

Most often , The final output of binocular stereo vision is in the left camera coordinate system XYZ coordinate , This paper takes these three components as the object of accuracy analysis .

First , Define some variables ：

$b$： Baseline length
$f$： The focal length
$x,y$ ： Like point coordinates （ Take the main point of the image as the origin ）
$X,Y,Z$： Coordinates in camera coordinate system
$d$： parallax

Let's first look at the solution formula of these three components ：
$$Z=\frac{bf}{d},X=\frac{Z}{f}x,Y=\frac{Z}{f}y$$

From the formula , In hardware parameters $B,f$ Fixed case ,$XYZ$ The value of is directly related to the coordinate value of the image point , $XYZ$ The accuracy of is actually the spatial deviation value under the image point accuracy , Therefore, we take the accuracy of image points as the basic （ Minimum ） Precision unit .

Suppose the image point $x,y$ The accuracy of is $s_x,s_y$, parallax $d$ The accuracy of is $s_d$. It is commonly believed $x,y$ The accuracy of is the same , namely $s_x=s_y=s$, Generally speaking, the accuracy of parallax can be calculated by formula $$s_d=\frac{s_x}{\sqrt{2}}$$ To estimate ¹.

Z Directional accuracy

First of all, for $Z=\frac{bf}{d}$, The independent variable is $d$, We are right. $d$ Finding partial derivatives , Available
$$\frac{\partial Z}{\partial d}=-\frac{bf}{d^2}=-\frac{Z^2}{bf}$$

therefore ,$Z$ The accuracy of the direction can be expressed as
$$s_Z=\frac{Z^2}{bf}{s}_d=\frac{Z^2}{\sqrt{2}bf}s$$

You know $Z$ Direction accuracy and $Z$ Square positive correlation of , That is, it is positively correlated with the square of the distance between the object and the camera （ Strictly speaking $Z$ Direction distance ）.

meanwhile , The above formula can change one form ：
$$s_Z=\frac{Z}{b}\frac{Z}{f}{s}_d$$

hypothesis $q=\frac{Z}{b},m=\frac{Z}{f}$, be $q$ Is what we are familiar with Base height ratio Reciprocal ,$m$ Is the scale of the image （ namely GSD, The space size represented by a pixel ）, This formula shows , Base height ratio and GSD Yes $Z$ Direction accuracy plays a key role , Larger base height ratio and smaller GSD Contribute to $Z$ Directional accuracy . This can be used to guide the design of binocular stereo vision system .

XY Directional accuracy

Empathy , about $X$, The independent variable is $Z$ and $x$, We are right. $Z$ and $x$ Finding partial derivatives , Available
$$\frac{\partial X}{\partial Z}=\frac{x}{f},\frac{\partial X}{\partial x}==\frac{Z}{f}$$

$X$ The directional accuracy can be expressed as
$$s_X=\sqrt{{(\frac{x}{f}{s}_Z)}^2+{(\frac{Z}{f}{s}_x)}^2}$$

Empathy ,$Y$ The directional accuracy can be expressed as
$$s_Y=\sqrt{{(\frac{y}{f}{s}_Z)}^2+{(\frac{Z}{f}{s}_y)}^2}$$

hold $s_Z=\frac{Z^2}{\sqrt{2}bf}s,s_x=s_y=s$ Generation into the formula , Available

$$s_X=\sqrt{1+{(\frac{xZ}{\sqrt{2}fb})}^2}\frac{Z}{f}s=\sqrt{1+{(\frac{X}{\sqrt{2}b})}^2}\frac{Z}{f}s$$
$$s_Y=\sqrt{1+{(\frac{yZ}{\sqrt{2}fb})}^2}\frac{Z}{f}s=\sqrt{1+{(\frac{Y}{\sqrt{2}b})}^2}\frac{Z}{f}s$$

It can be seen that ,$s_X$ and $s_Y$ It is of equal scale , Combine the previous formula ,
$$s_Z=\frac{Z^2}{\sqrt{2}bf}s$$

Get the precision expression of three directions .

X/Z Accuracy curve

In order to observe the three directions more clearly, the accuracy increases with $Z$ Trend of value change , Let's do a simulation , Suppose the accuracy of the image point is 10$\mu m$, Calculate and plot $Z$ and $X$ Direction （$Y$ Direction and $X$ Direction and other scales , The trend is the same ） Accuracy curve .

Simulation data of other parameters ：

$f=1100$ pix
$x=640$ pix
$b=200$ mm

The accuracy curve drawn is as follows ：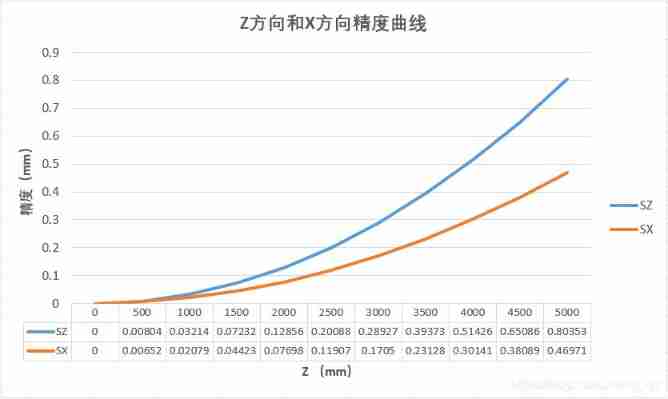

It can be seen from the results of precision calculation and trend chart , The accuracy value increases with $Z$ It becomes bigger with the increase of （ It means that the accuracy is getting worse ）, And when $Z$ When it's worth more ,$Z$ Directional accuracy ratio $X(Y)$ The direction accuracy is poor , With Z An increase in , The gap is more obvious .

And when $Z$ It's worth less ,$Z$ On the contrary, the direction accuracy will be better than $XY$ The direction is better , We will Z The range of is reduced to 0~500, Draw another curve ,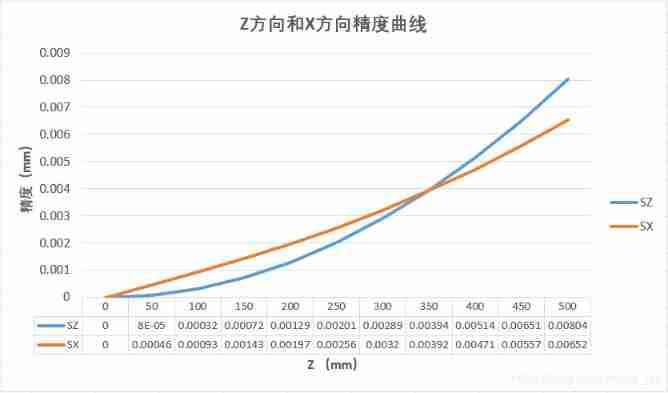

You can see , stay $Z$ Less than 350mm Left and right ,$Z$ The direction accuracy is better than $X$ Direction , This critical point $Z$ The value is calculated according to the hardware parameters and precision formula , And it is related to the coordinates of image points .

reference

- [1] Walker, Stewart. Close-Range Photogrammetry and 3D Imaging, 2nd Edition[J]. Photogrammetric Engineering & Remote Sensing, 2015.

About bloggers ：
Ethan Li Li Yingsong （ You know ： Li Yingsong ）
Wuhan University Doctor of photogrammetry and remote sensing
Main direction Stereo matching 、 Three dimensional reconstruction
2019 Won the first prize of scientific and technological progress in surveying and mapping in （ Provincial and ministerial level ）

Love 3D , Love sharing , Love open source
GitHub： https://github.com/ethan-li-coding
Personal wechat ：

Welcome to exchange ！
Bloggers focus on , More 3D reconstruction knowledge popular science , thank ！
Blog home page ：https://ethanli.blog.csdn.net