当前位置:网站首页>[paper reading] the latest transfer ability in deep learning: a survey in 2022
[paper reading] the latest transfer ability in deep learning: a survey in 2022
2022-07-05 08:08:00 【Prisoner CY】
- English title :Transferability in Deep Learning: A Survey
- Chinese title : A review of transferability in deep learning
- Paper download link :[email protected]
preface
On the whole, this review is quite detailed , Transfer learning itself is widely used in artificial intelligence , Therefore, it is easy to combine with other methods , The adaptability in the third section of the original text is very critical , It is also the key content of this note , It's very theoretical , The other two parts are relatively water , Many platitudes will not be recorded . Personally, I think it is more suitable to have a certain machine learning foundation , Then people who want to consolidate and transfer relevant knowledge to read .
Abstract
The success of deep learning algorithms generally depends on large-scale data, while humans appear to have inherent ability of knowledge transfer, by recognizing and applying relevant knowledge from previous learning experiences when encountering and solving unseen tasks. Such an ability to acquire and reuse knowledge is known as transferability in deep learning. It has formed the long-term quest towards making deep learning as data-efficient as human learning, and has been motivating fruitful design of more powerful deep learning algorithms. We present this survey to connect different isolated areas in deep learning with their relation to transferability, and to provide a unified and complete view to investigating transferability through the whole lifecycle of deep learning. The survey elaborates the fundamental goals and challenges in parallel with the core principles and methods, covering recent cornerstones in deep architectures, pre-training, task adaptation and domain adaptation. This highlights unanswered questions on the appropriate objectives for learning transferable knowledge and for adapting the knowledge to new tasks and domains, avoiding catastrophic forgetting and negative transfer. Finally, we implement a benchmark and an open-source library, enabling a fair evaluation of deep learning methods in terms of transferability.
List of articles
- preface
- Abstract
- 1 Introduction Introduction
- 2 Preliminary training Pre-Training
- 3 adaptive Adaptation
- 4 assessment Evaluation
- 5 Conclusion Conclusion
- reference
1 Introduction Introduction
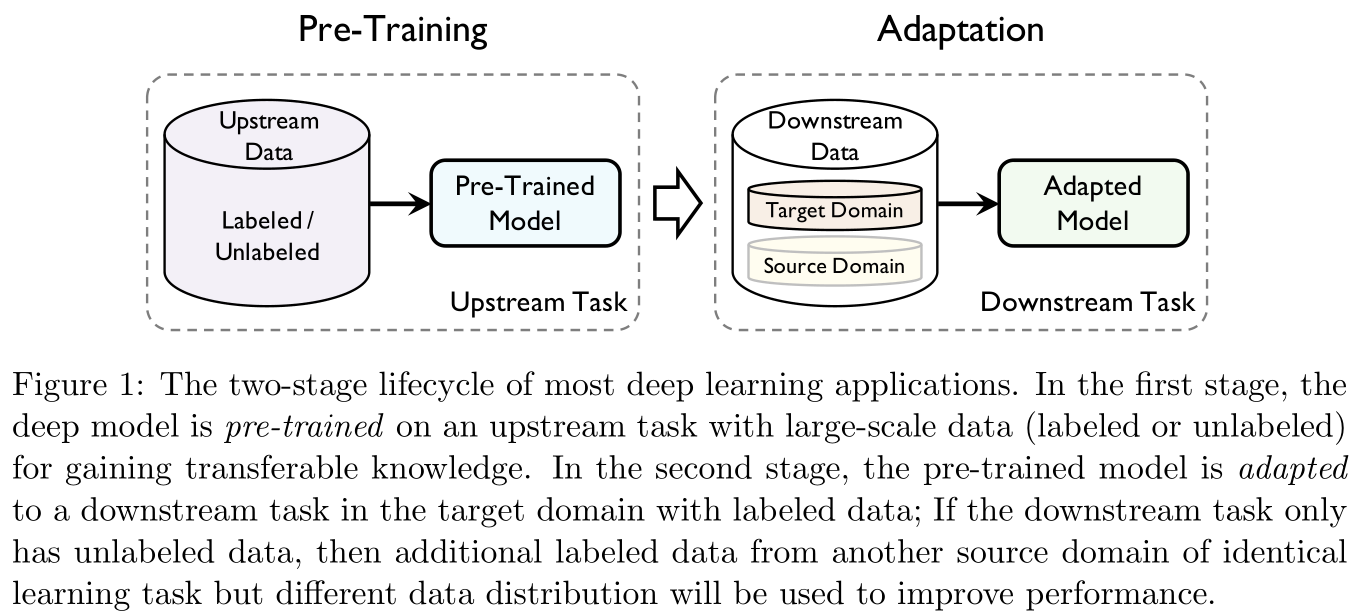
Pre training itself is a kind of transfer learning .
Transfer learning is divided into two stages : Preliminary training (pre-training) And To adapt to (adaptation). The former focuses on General portability (generic transferability), The latter focuses on specific Portability (specific transferability).
1.1 The term Terminology
| Mathematical notation | Specific meaning |
|---|---|
| X \mathcal X X | input space |
| Y \mathcal Y Y | Output space |
| f f f | f : X → Y f:\mathcal X\rightarrow \mathcal Y f:X→Y It is a annotation function that needs to be learned |
| l l l | l : Y × Y → R + l:\mathcal{Y}\times \mathcal{Y}\rightarrow \R_+ l:Y×Y→R+ Is the given loss function |
| D \mathcal D D | X \mathcal X X An unknown distribution on |
| D ^ \mathcal{\hat D} D^ | Independent identically distributed sampling from D \mathcal D D The sample of { x 1 , . . . , x n } \{ {\bf x}_1,...,{\bf x}_n\} { x1,...,xn} |
| P ( ⋅ ) P(\cdot) P(⋅) | It's defined in X \mathcal X X Probability of events on |
| E ( ⋅ ) \mathbb E(\cdot) E(⋅) | Mathematical expectation of random variables |
| U \mathcal U U | Upstream data |
| S \mathcal S S | Source field of downstream data |
| T \mathcal T T | Target areas of downstream data |
| t ∗ t_{*} t∗ | ∗ * ∗ The task of the field , ∗ * ∗ Can take T , S , U \mathcal{T,S,U} T,S,U |
| H \mathcal H H | Hypothetical space ( It can be understood as a model set ) |
| h h h | An assumption in a hypothetical space ( Unless otherwise specified in the following , Assumptions and models have the same meaning ) |
| ψ \psi ψ | Feature generator |
| θ \theta θ | Suppose the parameters |
| x \bf x x | Model input |
| y \bf y y | Model output |
| z \bf z z | Hidden layer feature activation generation results |
| D D D | Recognizer for distinguishing different distributions |
Definition 1 1 1( Portability ):
Given the source domain S \mathcal{S} S Learning tasks of t S t_{\mathcal{S}} tS And target areas T \mathcal T T Learning tasks of t T t_{\mathcal{T}} tT, Portability (transferability) From t S t_{\mathcal S} tS To acquire transferable knowledge , Put the acquired knowledge in t T t_{\mathcal T} tT And can make t T t_{\mathcal T} tT Of The generalization error Reduce , among S ≠ T \mathcal S\neq \mathcal T S=T or t S ≠ t T t_{\mathcal S}\neq t_{\mathcal T} tS=tT.
1.2 summary Overview
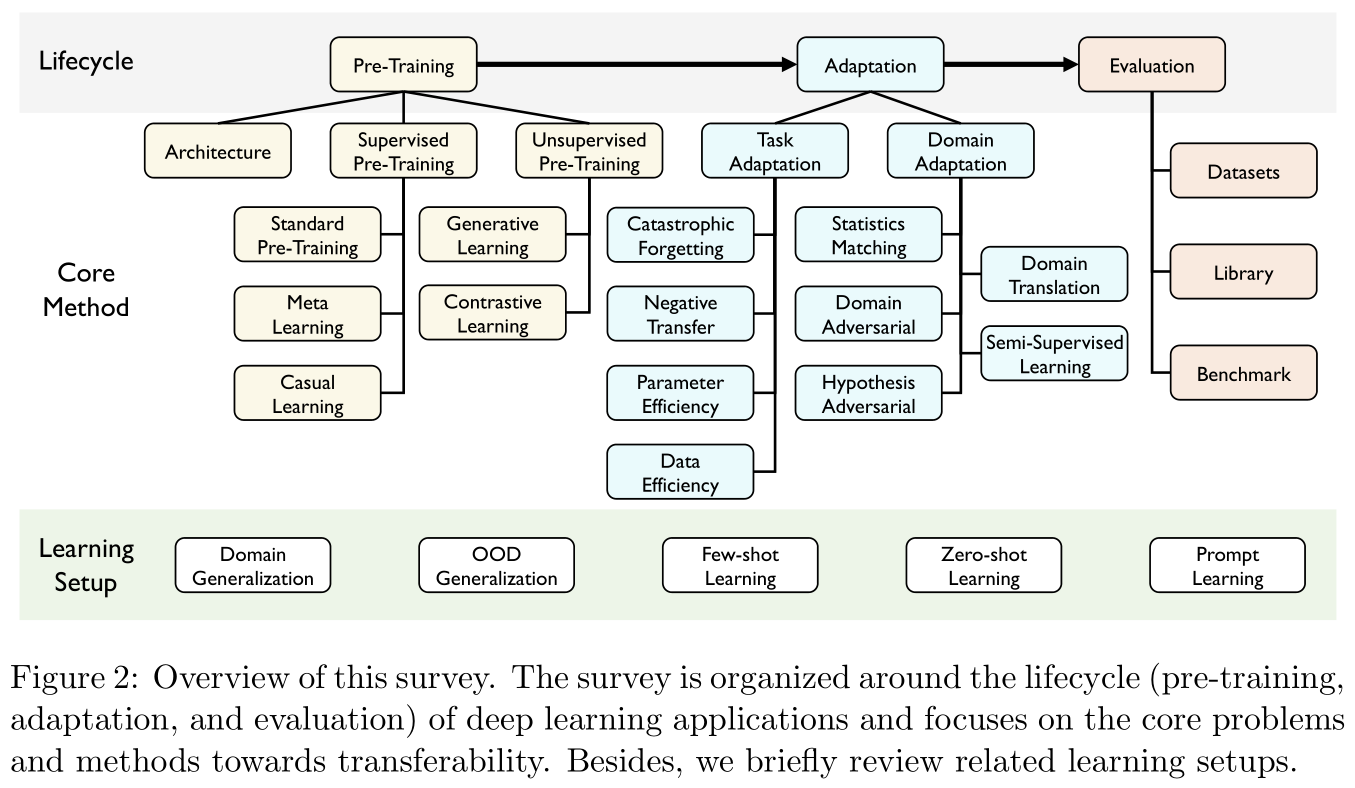
This paper is divided into three parts :
- Preliminary training (Pre-training): About some important migration model architectures , A summary of supervised and unsupervised pre training methods . This part is relatively simple , Only summarize and record the key contents .
- adaptive (Adaptation): A focus on Task adaptability (task adaptation) And Domain adaptability (domain adaptation), This part is highly theoretical , In especial Domain adaptability This part summarizes a large number of theorems and statistical results , I don't think it was written by the same person .
- assessment (Evaluation): This paper presents a general algorithm and evaluation of open source package for migration learning , Project address at [email protected]
2 Preliminary training Pre-Training
2.1 Pre training model Pre-Training Model
Generally speaking , The quality of pre training task learning directly affects the application performance of pre training model in downstream tasks .
Generally speaking , Pre training will be carried out on a very large number of data sets , So as RNN and CNN This model architecture with local connection assumptions is usually not used as a pre training model architecture ( Because there is enough data , There is no need to simplify the model architecture ), At present, the mainstream basic injuries are based on Transformer Large scale pre training model of . Compare with RNN and CNN,Transformer Almost no assumptions are made about the structure of the input data , That is, it can be used to deal with a wider range of data types .
The development of pre training model in transfer learning ( Such as Figure 3 Shown ):
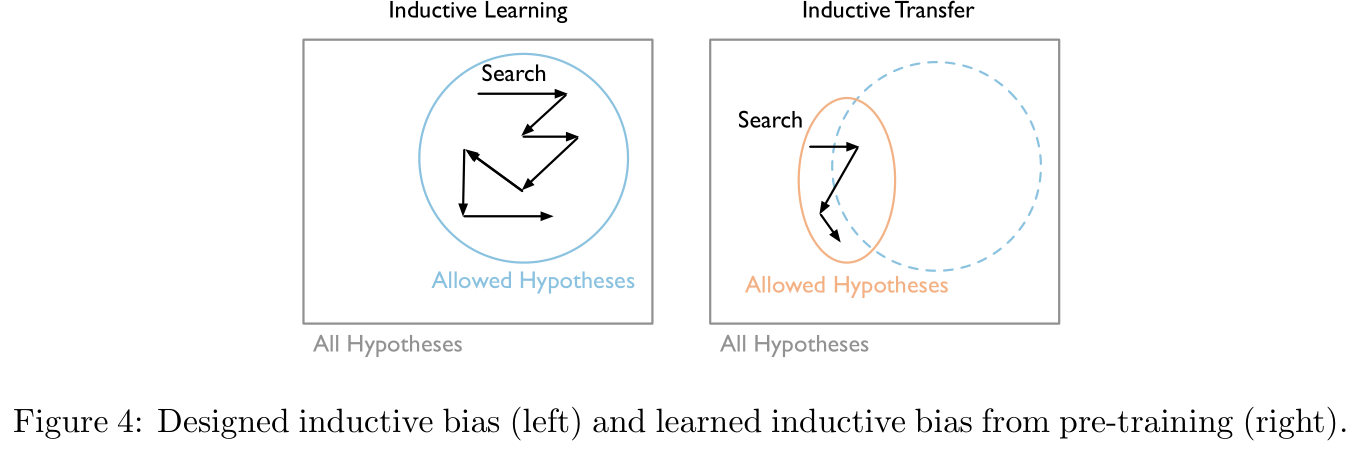
Figure 4 The middle and left figure shows the process of model parameter search during direct training , The right figure shows the model parameter search process after pre training migration , It means that the essence of pre training is to narrow the search scope of model parameters ( However, it seems that it can also be understood as finding a better starting point ):
2.2 Supervised pre training model Supervised Pre-training Model
The purpose of supervised pre training is to train the pre training model on large-scale labeled data , Then migrate to enhance downstream tasks ( Such as Figure 5 Shown ).
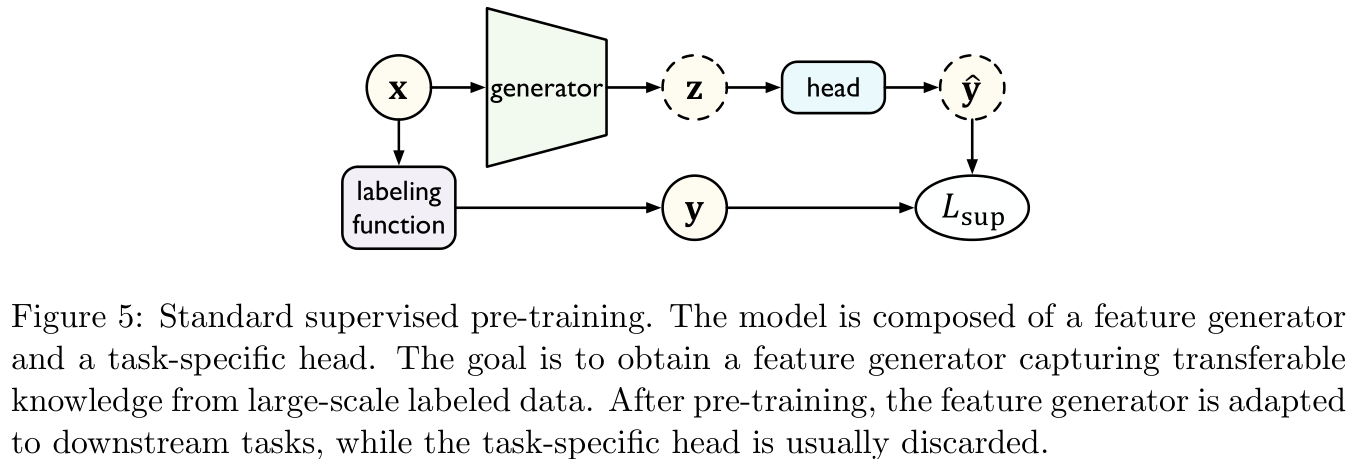
Standard supervised pre training is very useful in the case of labeled data volume reorganization , But sometimes it's for Opposite samples (adversarial examples) The existence of is extremely sensitive , This may affect the robustness of migration . Therefore, this section will focus on two other supervised pre training methods .
2.2.1 Meta learning Meta Learning
So-called Meta learning (meta-learning), Generally speaking, it means Learn how to learn , To improve the efficiency of migration . Its core is to Meta knowledge (meta knowledge) ϕ \phi ϕ Integrate with the model , Meta knowledge ϕ \phi ϕ Can capture different learning tasks Essential attribute (intrinsic properties), Also known as Meta training (meta-training). When a new task needs to be solved , Learned Meta knowledge Rescue can help target model parameters θ \theta θ Quickly adapt to new tasks , This process is called Meta test (meta-testing).
Such as Figure 6 Shown , The left figure is to simulate Meta test Rapid adaptation conditions in the process , The meta training data is constructed into a n n n A collection of learning tasks , Each task corresponds to a learning task i ∈ [ n ] i\in[n] i∈[n], Contains training sets for adapting to this task D i t r \mathcal{D}_i^{\rm tr} Ditr And test sets for evaluation D i t s \mathcal{D}_i^{\rm ts} Dits, The picture on the right shows Meta training The objective function of is a two-level optimization problem :
ϕ ∗ = argmax ϕ ∑ i = 1 n log P ( θ i ( ϕ ) ∣ D i t s ) , where θ i ( ϕ ) = argmax θ log P ( θ ∣ D i t r , ϕ ) (1) \phi^*=\text{argmax}_{\phi}\sum_{i=1}^n\log P(\theta_i(\phi)|\mathcal{D}_i^{\rm ts}),\quad\text{where }\theta_i(\phi)=\text{argmax}_{\theta}\log P(\theta|\mathcal{D}_i^{\rm tr},\phi)\tag{1} ϕ∗=argmaxϕi=1∑nlogP(θi(ϕ)∣Dits),where θi(ϕ)=argmaxθlogP(θ∣Ditr,ϕ)(1)
Here, the inner optimization is used to update the model parameters θ \theta θ, Outer layer optimization is used to find better Meta knowledge For migration , Meta learning The key is how to build Meta knowledge In the form of .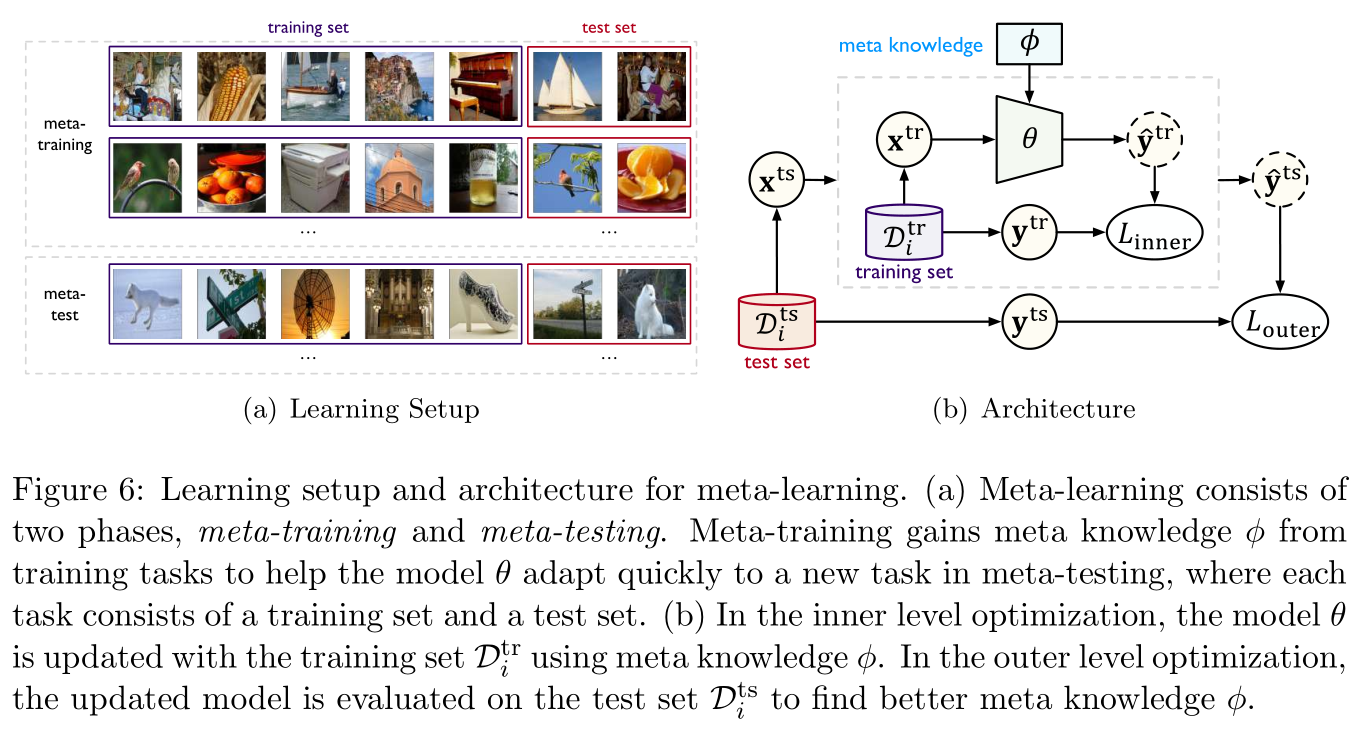
Memory based meta learning (memory-based meta-learning):
The controller will receive training data D i t r \mathcal{D}_i^{\rm tr} Ditr The knowledge mined in is written into memory , And read knowledge from memory to use basic learners θ \theta θ In the test data D i t r \mathcal{D}_i^{\rm tr} Ditr Make predictions on , The parameters of the controller will be constantly updated . I don't think this is a very novel method , In essence, some pre-processing data stored in advance when you are working on a project can be regarded as Memory based meta learning .
Such as references [ 150 ] [150] [150] Proposed Memory enhanced neural network (memory-augmented neural networks,MANN) take Binding samples represent class information (bound sample representation-class label information) Stored in external memory , Use for retrieval as a feature to predict . reference [ 121 ] [121] [121] Is to propose another memory mechanism , The basic learner is used to provide information about the status of the current task , Meta learners interact with external memory to generate model parameters for basic learners , Learn new tasks quickly .
Memory based meta learning For such as Less shooting classification (few-shot classification) And the downstream task of reinforcement learning is relatively advantageous , But we need to design black box architecture to merge memory mechanism , Often we don't know what is stored , And why stored things are beneficial to model migration .
Meta learning based on Optimization (optimization-based meta-learning):
This method examines the better initialization of the model as meta knowledge . Such as references [ 43 ] [43] [43] Proposed in Model agnostic meta learning (model-agnostic meta-learning,MAML) Directly find an initialization that is most suitable for migration tuning , That is, only a small amount of gradient descent iteration and a small amount of annotation data are needed to adapt to the new task . In order to learn such an initialization , For each sample task i ∈ [ n ] i\in[n] i∈[n], Model ϕ \phi ϕ First of all, its training data D i t r \mathcal{D}_i^{\rm tr} Ditr The last step is α \alpha α Gradient descent iteration :
θ i = ϕ − α ∇ ϕ L ( ϕ , D i t r ) (2) \theta_i=\phi-\alpha\nabla_{\phi}L(\phi,\mathcal{D}_i^{\rm tr})\tag{2} θi=ϕ−α∇ϕL(ϕ,Ditr)(2)
This is imitating from ϕ \phi ϕ This point starts to fine tune the model . As meta knowledge , ϕ \phi ϕ It should have good portability , So for all tasks i ∈ [ n ] i\in[n] i∈[n], Fine tuned parameters θ i \theta_i θi In the test set D i t s \mathcal{D}_i^{\rm ts} Dits The performance should be very good :
min ϕ ∑ i = 1 n L ( θ i ( ϕ ) , D i t s ) = ∑ i = 1 n L ( ϕ − − α ∇ ϕ L ( ϕ , D i t r ) , D i t s ) (3) \min_{\phi}\sum_{i=1}^nL(\theta_i(\phi),\mathcal{D}_i^{\rm ts})=\sum_{i=1}^nL(\phi--\alpha\nabla_{\phi}L(\phi,\mathcal{D}_i^{\rm tr}),\mathcal{D}_i^{\rm ts})\tag{3} ϕmini=1∑nL(θi(ϕ),Dits)=i=1∑nL(ϕ−−α∇ϕL(ϕ,Ditr),Dits)(3)
Notice MAML The meta knowledge dimension of is too high , So references [ 167 ] [167] [167] Use standard pre training as initialization to improve . in addition , reference [ 137 , 145 , 196 ] [137,145,196] [137,145,196] Also on the MAML Some improvements have been made .
Meta learning Your performance is not stable , Sometimes it's worse than the standard pre training method .
2.2.2 Causal learning Casual Learning
Causal learning (casual learning) Aim at Out of distribution (out-of-distribution,OOD) In the field Extrapolation (extrapolated) The migration study . Its core is to use some Causal mechanism (causal mechanisms) To capture the distribution of the complex real world , When the distribution changes , Only a few Causal mechanism change , The rest remains the same , In this way, we can get better OOD Extension . Specific as Figure 7 Shown :
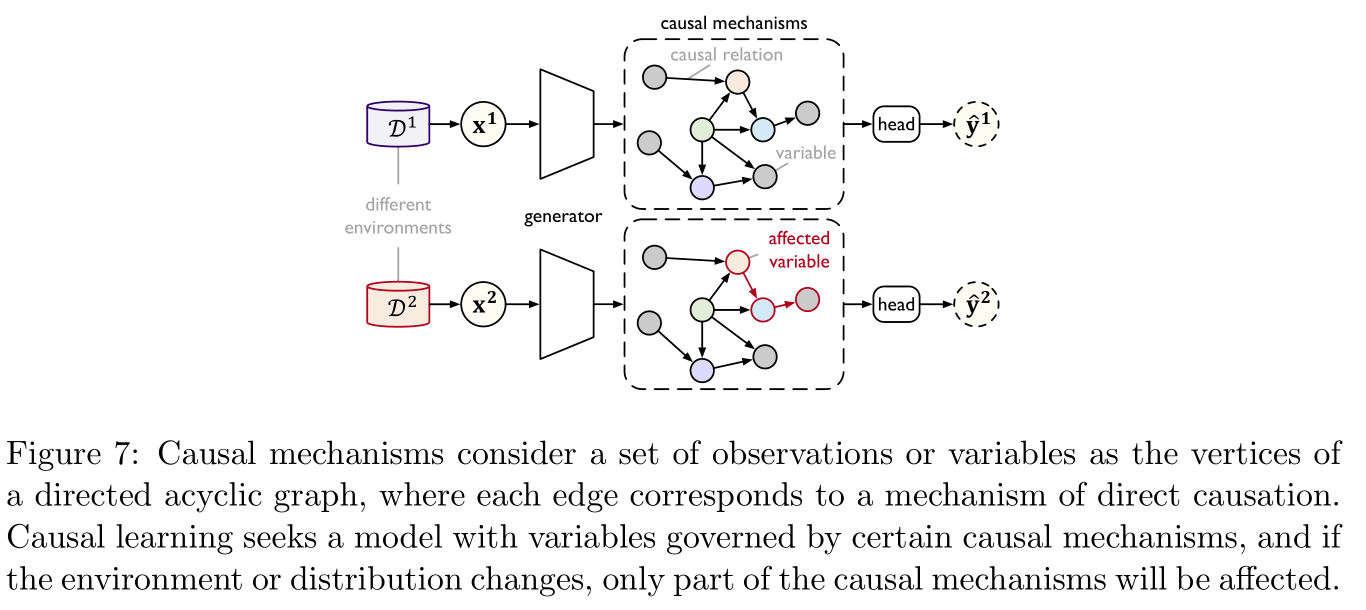
Causal mechanism Represented by the vertices of a directed acyclic graph as variables , Each edge represents a causal relationship , In this way, given the distribution of parent nodes , Get the joint distribution of each variable Non entangled factorization (disentangled factorization) form , At this time, some small changes in the distribution will only affect Non entangled factorization Local or in a sparse way . Causal learning The key problem is to obtain variables controlled by independent causal mechanisms , Here are two common methods :
Modular model (modular model): reference [ 56 , 31 ] [56,31] [56,31], In short, use LSTM perhaps GRU As the representation module of causal mechanism .
Constant learning (invariant learning): reference [ 129 , 4 ] [129,4] [129,4],
Here is the last reference [ 4 ] [4] [4] Methods , Given data represents ψ : X → Z \psi:\mathcal{X\rightarrow Z} ψ:X→Z, And the training environment E t r \mathcal{E}^{\rm tr} Etr, The conditional probability of representation and output is constant if there is a classifier h : Z → Y h:\mathcal{Z\rightarrow Y} h:Z→Y At the same time, it is optimal for all environments . It can be expressed as the following optimization problem with constraints :
minimize ψ : X → Z , h : Z → Y ∑ e ∈ E t r ϵ e ( h ∘ ψ ) subject to h ∈ argmin h ˉ : Z → Y ϵ e ( h ∘ ψ ) , ∀ e ∈ E t r (4) \begin{aligned} &\text{minimize}_{\psi:\mathcal{X\rightarrow Z},h:\mathcal{Z\rightarrow Y}}&&\sum_{e\in\mathcal{E}^{\rm tr}}\epsilon^{e}(h\circ\psi)\\ &\text{subject to}&&h\in\text{argmin}_{\bar h:\mathcal{Z\rightarrow Y}}\epsilon^{e}(h\circ\psi),\forall e\in\mathcal{E}^{\rm tr} \end{aligned}\tag{4} minimizeψ:X→Z,h:Z→Ysubject toe∈Etr∑ϵe(h∘ψ)h∈argminhˉ:Z→Yϵe(h∘ψ),∀e∈Etr(4)
among ϵ e ( h ∘ ψ ) \epsilon^{e}(h\circ\psi) ϵe(h∘ψ) It means in the environment e e e Medium predictor h ∘ ψ h\circ \psi h∘ψ Expected error of .
2.3 Unsupervised pre training model
Unsupervised pre training mainly refers to Self supervised learning (self-supervised learning), The focus is on how to build Self supervised learning Tasks are used for pre training , Methods can be divided into Generative learning (generative learning) And Comparative learning (contrastive learning) Two categories: .
2.3.1 Generative learning Generative Learning
Such as Figure 8 Shown , Generative learning An encoder is used in f θ f_{\theta} fθ Will disturb the input x ~ \bf \tilde x x~ Map to hidden layer representation z = f θ ( x ~ ) {\bf z}=f_{\theta}({\bf \tilde x}) z=fθ(x~), A decoder g θ g_{\theta} gθ Reconstruct the representation into an estimated input x ^ = g θ ( z ) {\bf \hat x}=g_{\theta}({\bf z}) x^=gθ(z), The model minimizes reconstruction errors L g e n ( x ^ , x ) L_{\rm gen}({\bf \hat x},{\bf x}) Lgen(x^,x) Training . The purpose of this is to give the model the ability to generate data distribution .
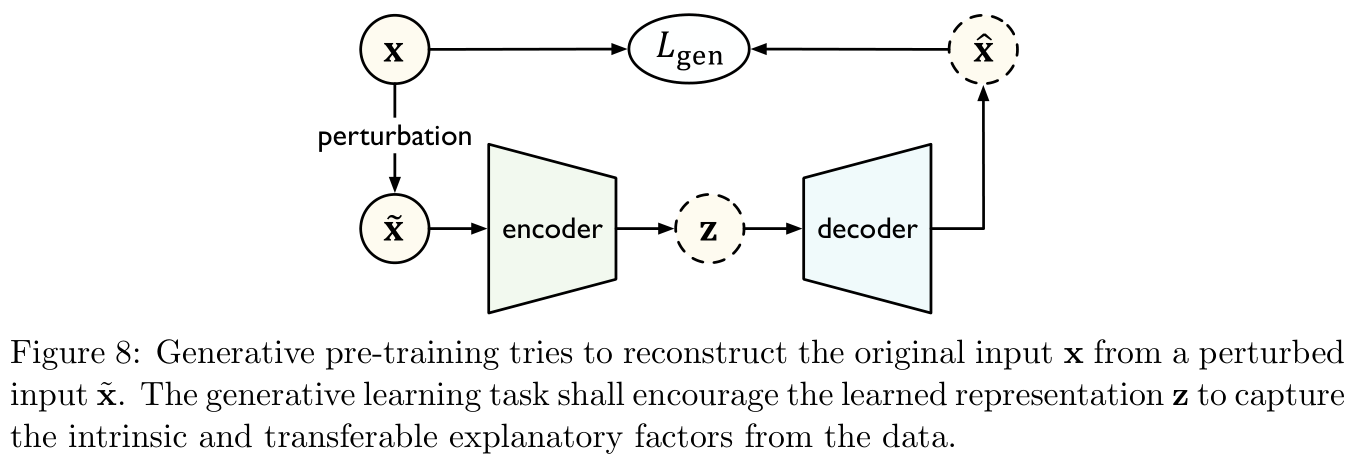
Generative learning Methods can be divided into two categories : Autoregressive model (auto-regressive) And Self coding model (auto-encoding).
Autoregressive model : A cliche , Such as Figure 9 Shown , Typical language models and their variants belong to autoregressive models .
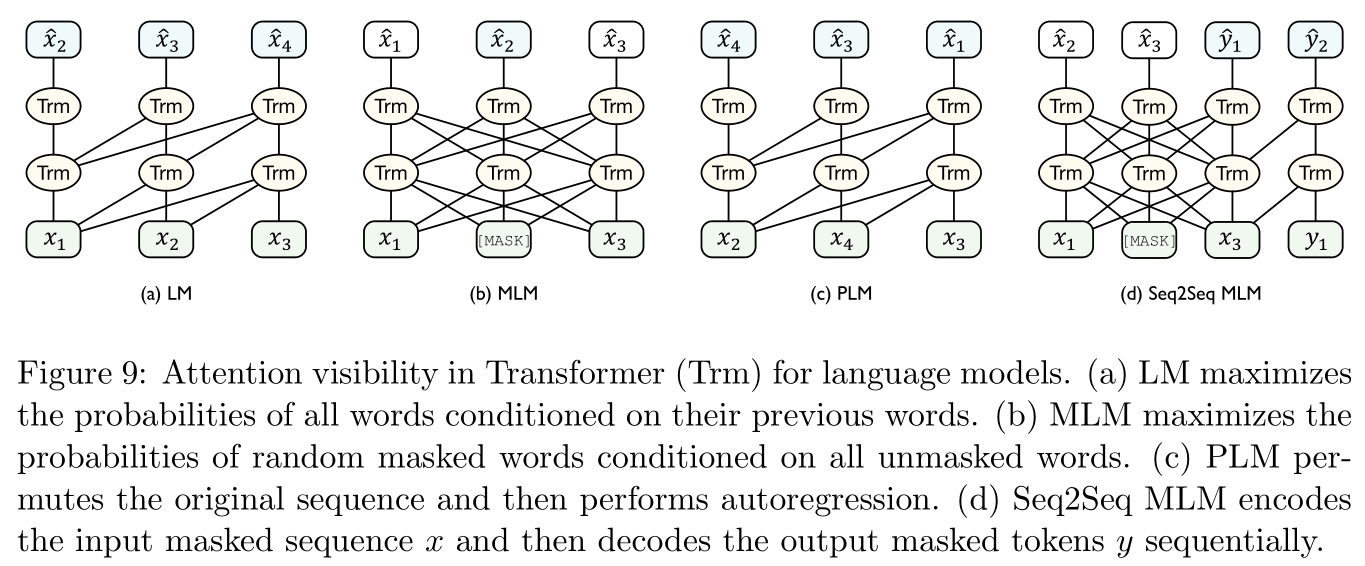
Given a sequence of text x 1 : T = [ x 1 , . . , x T ] {\bf x}_{1:T}=[x_1,..,x_T] x1:T=[x1,..,xT], The training goal of language model is to maximize the conditional probability of each word segmentation :
max θ ∑ t = 1 T log P θ ( x t ∣ x t − k , . . . , x t − 1 ) (5) \max_{\theta}\sum_{t=1}^T\log P_{\theta}(x_t|x_{t-k},...,x_{t-1})\tag{5} θmaxt=1∑TlogPθ(xt∣xt−k,...,xt−1)(5)
classical GPT Model ( reference [ 134 ] [134] [134]) It belongs to autoregressive model .Self coding model : The idea is to approximate the data distribution by generating raw data according to the coding representation , common BERT Model belongs to self coding model .
stay Figure 9 In the last picture in Cover up the language model (Masked Language Model,MLM, This is also BERT Mechanisms used in model training ), First use [ M A S K ] \rm [MASK] [MASK] Mark in the input statement x {\bf x} x Cover up some participles randomly m ( x ) m({\bf x}) m(x), Then train the model according to the remaining word segmentation x \ m ( x ) {\bf x}_{\backslash m({\bf x})} x\m(x) To predict these cover up participles :
max θ ∑ x ∈ m ( x ) log P θ ( x ∣ x \ m ( x ) ) (6) \max_{\theta}\sum_{x\in m({\bf x})}\log P_{\theta}(x|{\bf x}_{\backslash m({\bf x})})\tag{6} θmaxx∈m(x)∑logPθ(x∣x\m(x))(6)
This kind of cover up is very common .Autoregressive self coding hybrid model :
stay Figure 9 The third figure in Permutation language model (permuted language model,PLM, reference [ 195 ] [195] [195]) First, the order of the sampled statement sequence is replaced randomly , Then autoregressive prediction is carried out on the replaced series . Other classical models are trained in a similar way ( That is, both hollowed out , Change the order again ), such as T5 Model ( reference [ 136 ] [136] [136]),RoBERTa( reference [ 109 ] [109] [109]),ERNIE( reference [ 168 ] [168] [168]),SpanBERT( reference [ 83 ] [83] [83]),BART( reference [ 98 ] [98] [98]),GPT-3( reference [ 18 ] [18] [18]), Multilingual BERT( reference [ 132 ] [132] [132]),XLM( reference [ 91 ] [91] [91]).
2.3.2 Comparative learning Contrastive Learning
Such as Figure 10 Shown , stay Comparative learning in , There are two different View (views), Inquire about x q {\bf x}^q xq And key x k {\bf x}^k xk( From raw data x {\bf x} x Build to get ), The encoder maps different views to the hidden layer representation , The decoder further maps the hidden layer representation to Indicator space (metric space). The goal of model learning is to minimize the same sample x {\bf x} x The distance between the query and the key .
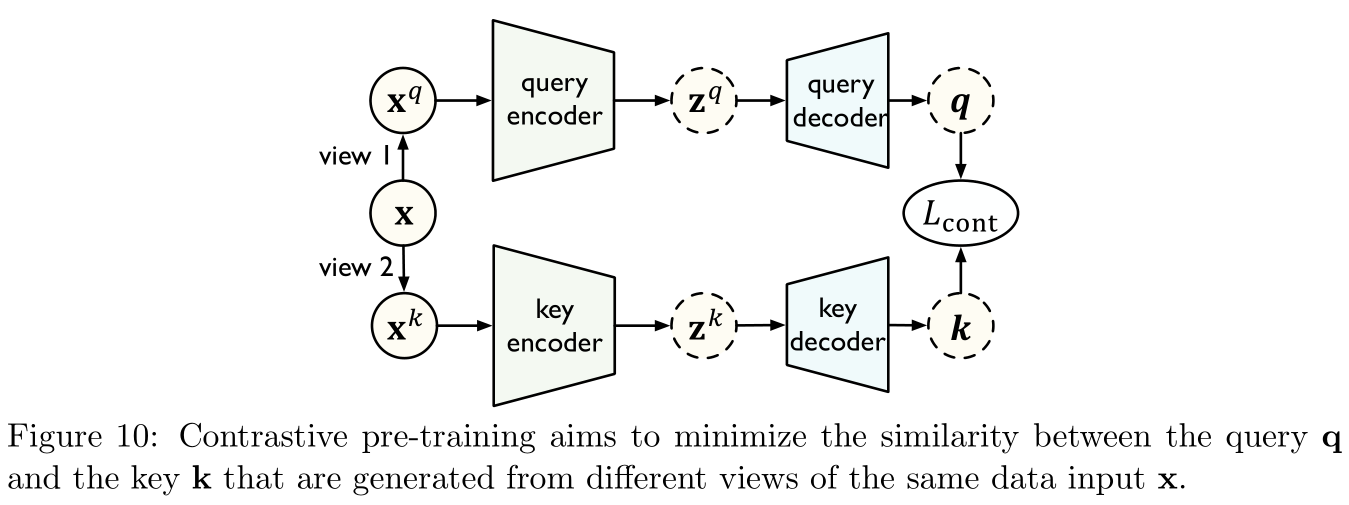
Typical contrastive learning methods :
Maximizing mutual information (mutual information maximization):
With references [ 70 ] [70] [70] Proposed Maximize depth information (Deep InfoMax) The model, for example , It aims to learn from the relationship between high-level global context and low-level local features to obtain a transferable representation . To be specific , A given input x {\bf x} x, Model learning an encoder ψ \psi ψ To maximize x {\bf x} x Between input and output Mutual information , Mutual information You can train a Discriminator (discriminator) D D D To distinguish their joint distribution from Marginal value (marginals) Product to be estimated and constrained . By using Noise comparison estimate (noise-contrastive estimation,NCE) Method , The training objectives of the model are :
max ψ E x ∼ U [ D ( x , ψ ( x ) ) − E x ′ ∼ U ~ ( log ∑ x ′ e D ( x ′ , ψ ( x ) ) ) ] (7) \max_{\psi}\mathbb{E}_{ {\bf x}\sim\mathcal U}\left[D({\bf x},\psi({\bf x}))-\mathbb{E}_{ {\bf x}'\sim\mathcal{\tilde U}}\left(\log\sum_{\bf x'}e^{D({\bf x}',\psi({\bf x}))}\right)\right]\tag{7} ψmaxEx∼U[D(x,ψ(x))−Ex′∼U~(logx′∑eD(x′,ψ(x)))](7)
among x \bf x x It is from the training distribution of upstream tasks U \mathcal U U Input samples obtained by sampling in , x ′ \bf x' x′ Is from another distribution U ~ = U \mathcal {\tilde U}=\mathcal U U~=U Samples obtained by sampling in , D D D It is used to distinguish the product of joint distribution and marginal value .Other related work includes references [ 124 , 178 , 135 ] [124,178,135] [124,178,135], The last one deals with the problem of zero projection .
Relevant location prediction (relative position prediction):
Here's the main thing The next prediction (next sentence prediction,NSP) Mission , For the first time in BERT Use... In the model , After that, classic ALBERT Model ( reference [ 93 ] [93] [93]) It also uses a similar pre training strategy .
Examples distinguish (instance discrimination):
Here are the references [ 191 ] [191] [191] Of InstDisc Model , It aims to learn the transferable representation according to the relationship between samples . To be specific , Given n n n A sample , Training encoder ψ \psi ψ Used to distinguish different samples , That is, minimize the query of the same sample q \bf q q And key k + {\bf k}_+ k+ Distance between ( This is also called the entire sample ), And maximize the query between different samples q \bf q q And key k + {\bf k}_+ k+ Distance between ( This is also called negative sample ):
min ψ − log exp ( q ⋅ k + / τ ) ∑ j = 0 K exp ( q ⋅ k j / τ ) (8) \min_{\psi}-\log\frac{\exp({\bf q}\cdot{\bf k}_+/\tau)}{\sum_{j=0}^K\exp({\bf q}\cdot{\bf k}_j/\tau)}\tag{8} ψmin−log∑j=0Kexp(q⋅kj/τ)exp(q⋅k+/τ)(8)
among τ \tau τ Is a super parameter used to control softmax The offset degree of the value , K K K Is the number of negative samples , In fact, this is negative sampling .Such as Figure 11 Shown ,InstDisc The model uses a Memory module (memory bank) To store the most recently updated representation of each key , This increases the number of negative samples , May lead to inconsistent feature representation :
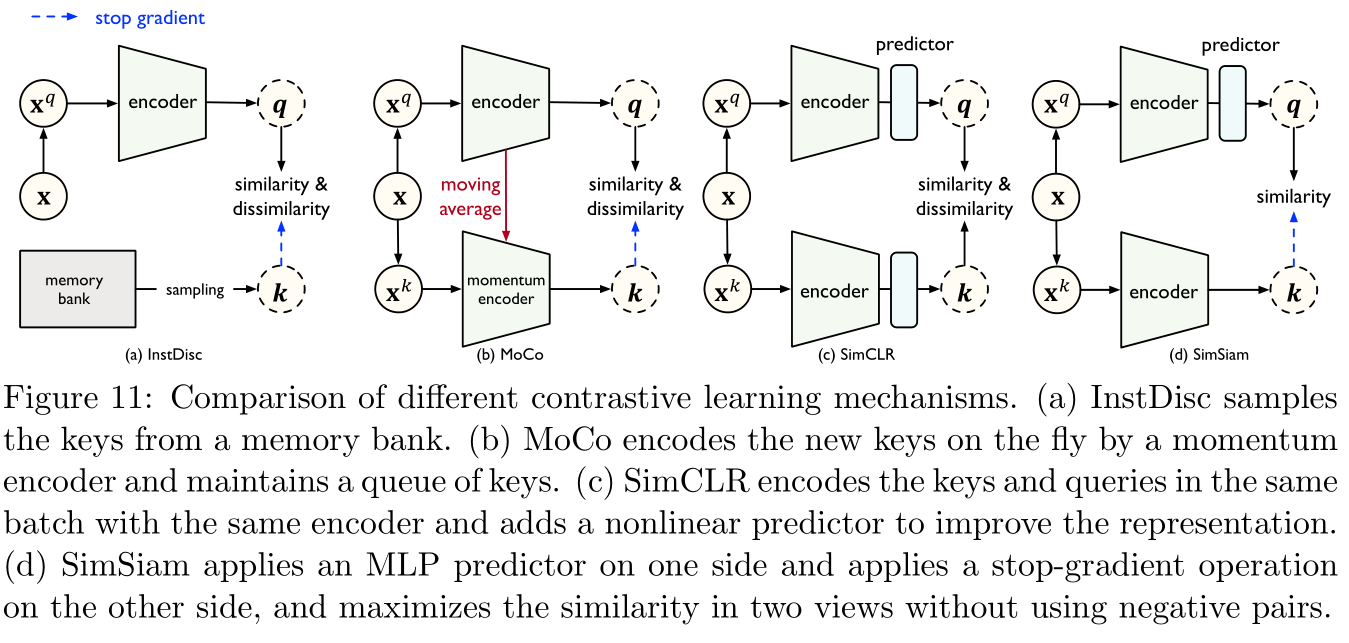
Other related studies include references [ 67 , 171 , 23 , 59 , 25 , 206 ] [67,171,23,59,25,206] [67,171,23,59,25,206]
2.4 notes Remarks
Summarize the performance of all methods in this section :
| Method | Modal ductility | Task extensibility | Data efficiency | Mark the cost |
|---|---|---|---|---|
| Standard pre training | optimal | in | optimal | Bad |
| Meta learning | optimal | Bad | Bad | Bad |
| Causal learning | in | Bad | Bad | Bad |
| Generative learning | in | optimal | optimal | optimal |
| Comparative learning | Bad | optimal | optimal | optimal |
Field description :
- Modal ductility (modality scalability): Can it be used for multimodal data , Text 、 picture 、 Audio-visual .
- Task extensibility (task scalability): Can you easily migrate the pre training model to different downstream tasks .
- Data efficiency (data efficiency): Can we get strong mobility through large-scale pre training .
- Mark the cost (labeling cost): Whether to rely on manual data annotation .
3 adaptive Adaptation
3.1 Task adaptability Task Adaptation
So-called Task adaptability (task adaptation), Given a pre training model h θ 0 h_{\theta^0} hθ0 And target areas T ^ = { x i , y i } i = 1 m \mathcal{\hat T}=\{ {\bf x}_i,{\bf y}_i\}_{i=1}^m T^={ xi,yi}i=1m( Tagged m m m A sample is right ), Our aim is to assume space accordingly H \mathcal{H} H Find a specific assumption in h θ : X → Y h_{\theta}:\mathcal X\rightarrow \mathcal Y hθ:X→Y, Make the risk ϵ T ( h θ ) \epsilon_{\mathcal T}(h_{\theta}) ϵT(hθ) To minimize the .
generally speaking , There are two ways to adapt the pre training model to downstream tasks :
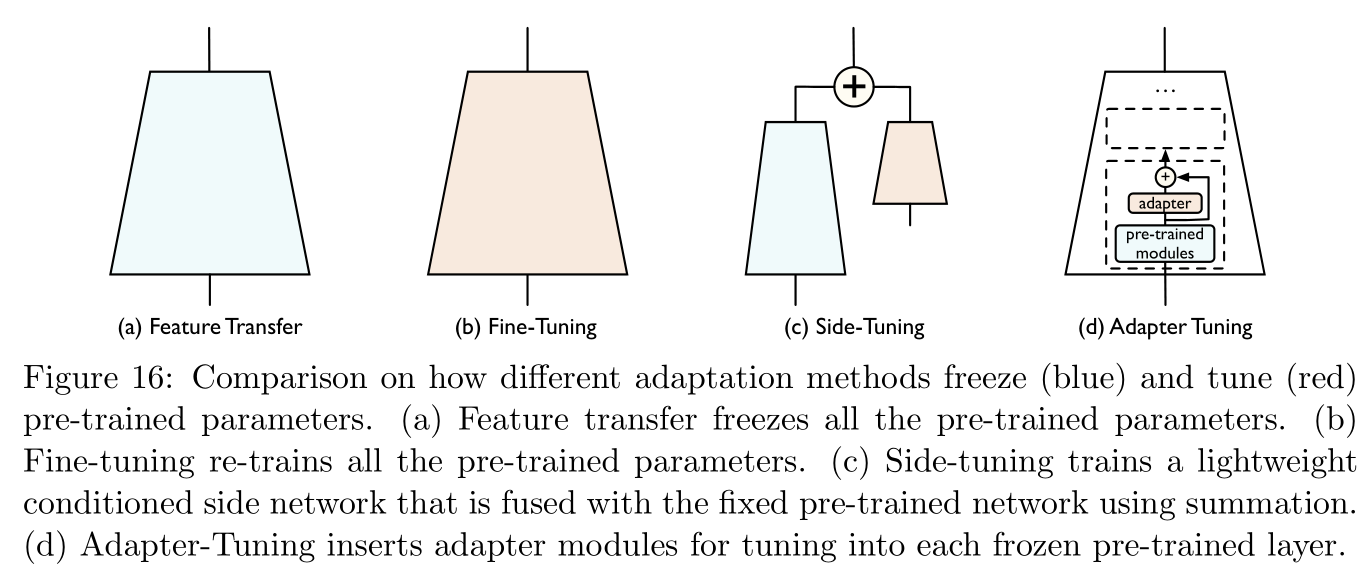
- Feature conversion (feature transfer): At this time, the network layer weight of the pre training model will be fixed , Just train a fully connected network for input feature transformation .
- fine-tuning (finetune): At this time, the network layer weight of the pre training model is equivalent to an initial point of model training , We will continue to train and optimize its network layer weight in the sample pair of the target field .
Feature conversion Convenient operation 、 Less cost , but fine-tuning The resulting model usually performs better .
Here is a concept called Benchmark trim (vanilla finetune), That is, directly on the target data , according to Experience risk minimization (empirical risk minimization) Fine tune the pre training model , But this method will be affected Catastrophic oblivion (catastrophic forgetting) And Negative transfer (negative transfer) The trouble with the problem ,Section 3.1.1 And Section 3.1.2 It mainly discusses how to alleviate these two problems . In addition, because the size of the model and the amount of training data are getting larger and larger ,Section 3.1.3 And Section 3.1.4 Will explore Parameter efficacy (parameter efficiency) And Data efficiency (data efficiency) The problem of .
3.1.1 Catastrophic oblivion Catastrophic Forgetting
Catastrophic oblivion The first concept of the concept of Lifelong learning (lifelong learning) It is proposed that , It means that the machine learning model will gradually lose the knowledge learned from the previous task when it is trained in a new task ( reference [ 86 ] [86] [86]).
In the fine-tuning link , Due to the scarcity of labeled data , It may cause the model to be trained to over fit on the target data , This phenomenon is called Token collapse (representational collapse, reference [ 2 ] [2] [2]).
The traditional solution is to train the model with a small learning rate and Stop early (early-stopping) Strategy , But it is easy to make the model fall into local optimization , Some relatively new research methods :
- reference [ 197 ] [197] [197]: It is found that the portability of different network layers in the model is different , Therefore, the training methods of treating different network layers during migration should be different ;
- reference [ 112 ] [112] [112]: Based on the above findings , Put forward Deep adaptation to the Internet (deep adaptation network,DAN), In this network architecture Specific task header (task-specific head) The learning rate of is ten times that of other layers ;
- reference [ 74 ] [74] [74]: Gradually from the last layer of the pre training model thaw (unfreeze) Network layer weights up to the first layer , This can effectively retain the pre training knowledge in the first layer .
- reference [ 62 ] [62] [62]: Put forward a new idea based on Policy network (policy networks) Reinforcement learning algorithm guidance fine tuning .
Two ways to fine tune :
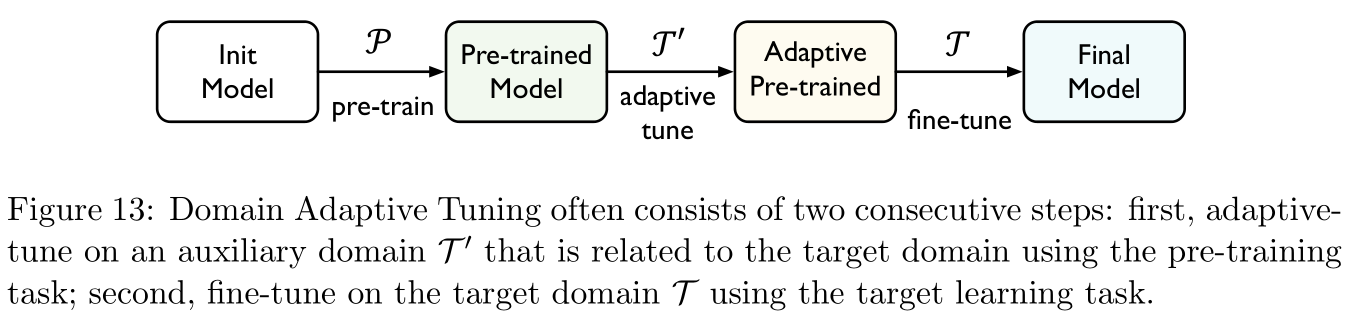
Domain adaptation tuning (domain adaptive tuning): reference [ 74 , 63 , 32 ] [74,63,32] [74,63,32]
Refers to the pre training model in the source domain , Then optimize the training samples in the target field , Usually, the pre training task is unsupervised , Such as Figure 13 Shown , reference [ 74 , 63 ] [74,63] [74,63] It is proposed that when fine-tuning, we will first perform an adaptive task related to the pre training task T ′ \mathcal T' T′ Fine tune on , Then in the target area T \mathcal T T Fine tune on , Two stage fine tuning can often be achieved Multi task learning (multi-task learning) Combine technology .
Regularization tuning (regularization tuning): reference [ 86 , 101 , 103 , 202 , 79 ] [86,101,103,202,79] [86,101,103,202,79]
min θ ∑ i = 1 m L ( h θ ( x i ) , y i ) + λ ⋅ Ω ( θ ) (9) \min_{\theta}\sum_{i=1}^mL(h_{\theta}({\bf x}_i),{\bf y}_i)+\lambda\cdot\Omega(\theta)\tag{9} θmini=1∑mL(hθ(xi),yi)+λ⋅Ω(θ)(9)
among L L L Is the loss function , Ω \Omega Ω Is the general form of regular term ( Such as Ω ( θ ) = ∥ θ ∥ 2 2 / 2 \Omega(\theta)=\|\theta\|_2^2/2 Ω(θ)=∥θ∥22/2 That is to say L 2 L_2 L2 The regularization ), λ \lambda λ It's the penalty factor .Record references here [ 86 ] [86] [86] Proposed Elastic weight merging (Elastic Weight Consolidation,EWC) Regular terms used in :
Ω ( θ ) = ∑ j 1 2 F j ∥ θ j − θ j 0 ∥ 2 2 (10) \Omega(\theta)=\sum_j\frac12F_j\|\theta_j-\theta_j^0\|_2^2\tag{10} Ω(θ)=j∑21Fj∥θj−θj0∥22(10)
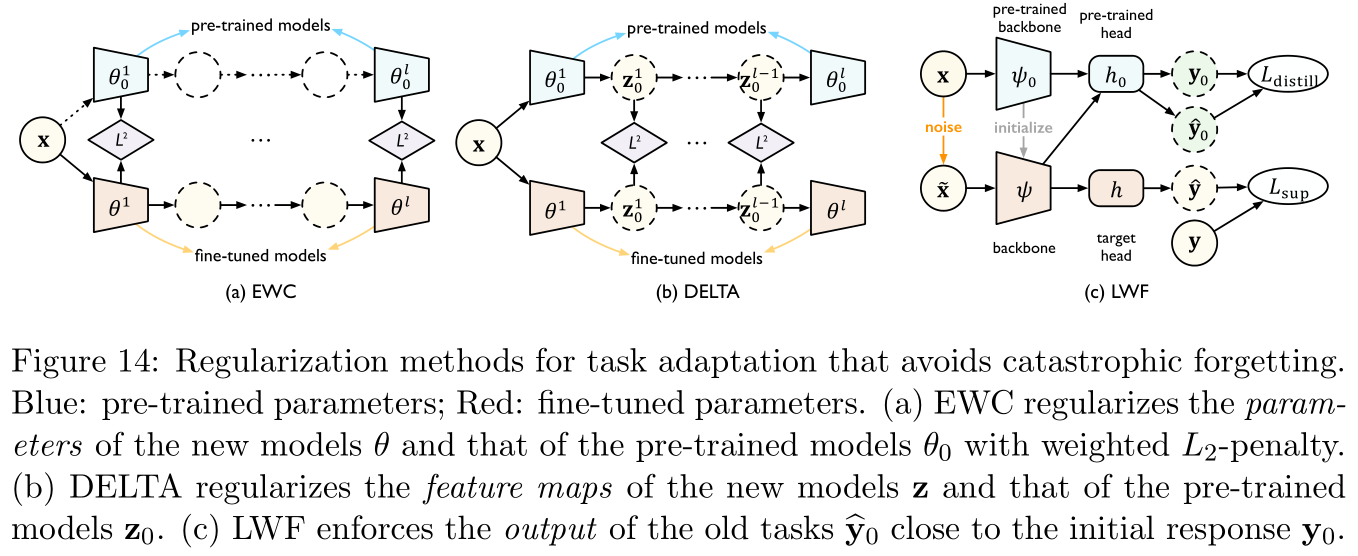
among F F F yes Fisher information matrix estimator (estimated Fisher information matrix), θ j \theta_j θj And θ j 0 \theta_j^0 θj0 They are the parameters of the network layer corresponding to the fine tuned model and the pre training model , The essence of the regular term is to hope that fine tuning will not change the network layer weight of the pre training model too much .in fact ,EWC The assumption is that if the weights of the network layers are similar , Then their output is also similar , But because the size of neural network is getting larger , Small changes in the weight of the network layer are very easy to produce the butterfly effect , Therefore, there are two other references in the sea area [ 101 , 103 ] [101,103] [101,103] Proposed DELTA And LWF, The former regularizes the difference between the output characteristics of the network layer corresponding to the pre training model and the fine-tuning model , The latter regularizes the difference between the final output results of the model , See Figure 14:
Another idea of regularization is based on the essence of regularization, which is to make the model smoother , So references [ 202 , 79 ] [202,79] [202,79] Directly through, in the case of small disturbance to the model input , The model output cannot change much , To force smooth models , The regular term thus constructed is :
Ω ( θ ) = ∑ i = 1 m max ∥ x ~ i − x ∥ p ≤ ϵ L s ( h θ ( x ~ i ) , h θ ( x i ) ) (11) \Omega(\theta)=\sum_{i=1}^m\max_{\|\tilde {\bf x}_i-{\bf x}\|_p\le\epsilon}L_s(h_{\theta}(\tilde {\bf x}_i),h_{\theta}({\bf x}_i))\tag{11} Ω(θ)=i=1∑m∥x~i−x∥p≤ϵmaxLs(hθ(x~i),hθ(xi))(11)
among ϵ > 0 \epsilon>0 ϵ>0 Is a small positive number , x i {\bf x}_i xi And x ~ i \tilde{\bf x}_i x~i It is the model input before and after disturbance , L s L_s Ls Is a loss function that measures the distance between the outputs of two models , For example, symmetry for classification KL Divergence or mean square error .The last other regularization method is based on the parameter update strategy :
- reference [ 89 ] [89] [89]: Random standardization (stochastic normalization), That is, randomly use Batch regularization layer (batch-normalization layer, reference [ 77 ] [77] [77]) Of statistic (statistics) To replace the target statistics , Thus, as an indirect regularization to reduce the dependence on the target statistics .
- reference [ 96 ] [96] [96]: Directly replace the fine-tuning model weight with part of the pre training model weight .
- reference [ 193 ] [193] [193]: According to a certain standard, only some parameters are selected to update in fine-tuning .
3.1.2 Negative transfer Negative Transfer
Negative transfer (negative transfer) The concept of is defined by references [ 142 ] [142] [142] Put forward .
reference [ 187 ] [187] [187] Further propose to measure the relationship between different fields Negative transfer Degree method , This paper extends this idea to pre training and fine tuning .
Definition 2 2 2( Negative migration gap ):
h θ ( U , T ) h_{\theta}(\mathcal{U,T}) hθ(U,T) Indicates data from upstream U \mathcal U U The pre trained model is adapted to the target data T \mathcal T T One of the models in , h θ ( ∅ , T ) h_{\theta}(\emptyset,\mathcal T) hθ(∅,T) Direct from T \mathcal T T The model trained on , be Negative migration gap (negative transfer gap) Defined as :
NTG = ϵ T ( h θ ( U , T ) ) − ϵ T ( h θ ( ∅ , T ) ) (12) \text{NTG}=\epsilon_{\mathcal T}(h_{\theta}(\mathcal{U,T}))-\epsilon_{\mathcal T}(h_{\theta}(\emptyset,\mathcal{T}))\tag{12} NTG=ϵT(hθ(U,T))−ϵT(hθ(∅,T))(12)
Say something happened Negative transfer , if NTG \text{NTG} NTG Being positive .
The authors note :
According to the definition , NTG \text{NTG} NTG It measures the performance gap between the migrated model and the directly trained model ( The difference between the values of the loss function ). if NTG \text{NTG} NTG Being positive , That's what happened Negative transfer , This shows that the model obtained by migration is not as good as the model obtained by training directly from the target data , Then migration itself is meaningless .
Negative transfer The reason for this :
Situations where the relevance between upstream tasks and downstream tasks is not high ( The distribution drift is too large ): reference [ 109 , 207 ] [109,207] [109,207] It is the case in word segmentation prediction and document classification ;
Depends on the marked target data size : It's not that the bigger the better , reference [ 187 , 66 ] [187,66] [187,66] Just explain ImageNet The pre training model is used in large-scale entity discovery dataset ( such as COCO Data sets ) Your performance is not very ideal ;
Depends on the task adaptation algorithm : An ideal adaptive algorithm should be able to improve the positive migration between related tasks and avoid the negative migration between unrelated tasks , But the two are actually contradictory , Specific as Figure 15 Shown :
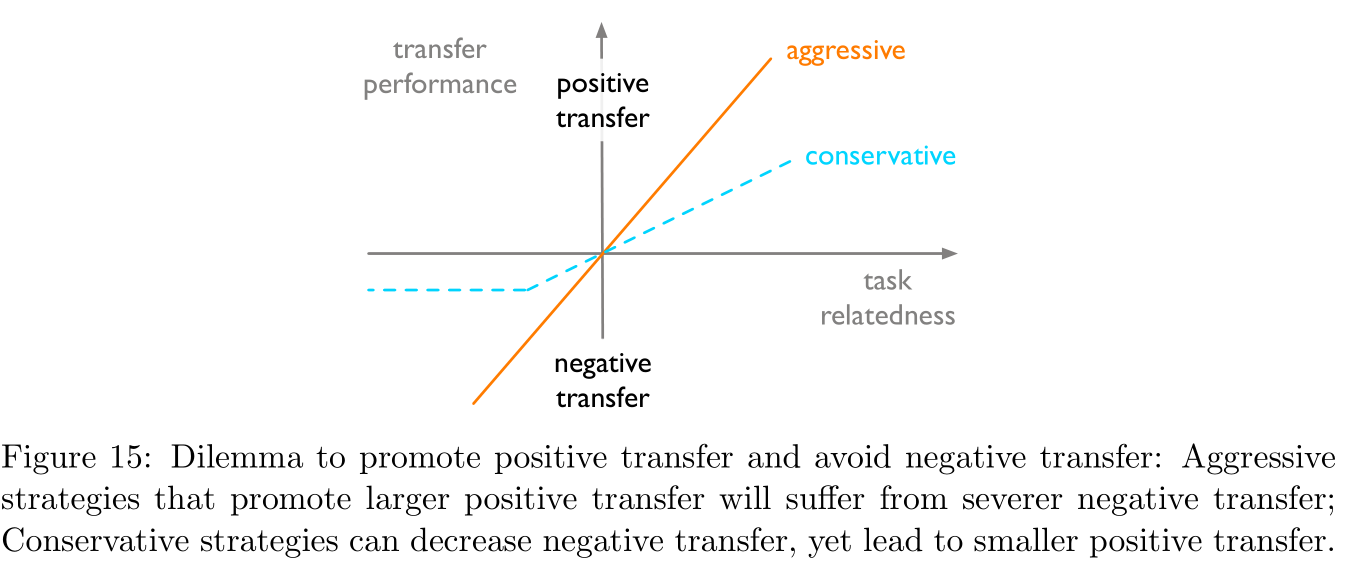
avoid Negative transfer Methods :( In this part, I feel that most of the nonsense , Pure rounding words )
- Enhance secure migration (enhancing safe transfer): reference [ 27 , 78 , 160 , 186 ] [27,78,160,186] [27,78,160,186], It refers to identifying the harmful knowledge in the pre training model .
- Select the correct pre training model : reference [ 199 , 123 , 198 , 68 , 23 ] [199,123,198,68,23] [199,123,198,68,23]
3.1.3 Parameter efficacy Parameter Efficiency
Parameter efficacy (parameter efficiency) What is investigated is that the pre training model will generate a complete set of model parameters for each downstream task , This is very disadvantageous in storage . One solution is to use references [ 20 ] [20] [20] Proposed Multi task learning technology , That is, fine tune a model to solve multiple target tasks , It may be beneficial to every target task . The problem is that multiple target tasks may not be highly correlated , At this time, you still need to fine tune them separately , And Multi task learning You need to access every target task at the same time , This is in Online scene (online scenarios) Is impossible ( Goals and tasks come one after another ).
promote Parameter efficacy Methods :
Residual tuning (residual tuning): reference [ 64 , 203 , 73 , 139 , 183 ] [64,203,73,139,183] [64,203,73,139,183]
The idea of residual optimization stems from the fact that fitting residual is easier than fitting function directly . Only references are recorded here [ 64 ] [64] [64] Methods ( Other articles are too general , There is no reference significance ), Fixed pre training model h p r e t r a i n e d h_{\rm pretrained} hpretrained The weight , Train a new model extra h s i d e h_{\rm side} hside To fit the residuals , The final model is h ( x ) = α h p r e t r a i n e d + ( 1 − α ) h s i d e h(x)=\alpha h_{\rm pretrained}+(1-\alpha)h_{\rm side} h(x)=αhpretrained+(1−α)hside, Be careful α \alpha α It can change during training .
Parameter difference tuning (parameter difference tuning): reference [ 62 , 103 , 119 ] [62,103,119] [62,103,119]
θ t a s k = θ p r e t r a i n e d ⊕ δ t a s k (13) \theta_{\rm task}=\theta_{\rm pretrained}\oplus\delta_{\rm task}\tag{13} θtask=θpretrained⊕δtask(13)
among ⊕ \oplus ⊕ Is the addition of element levels ( In fact, it is no different from ordinary addition ), θ p r e t r a i n e d \theta_{\rm pretrained} θpretrained Is a fixed pre training model weight , δ t a s k \delta_{\rm task} δtask It is the residual weight of different specific tasks , Here's what we're trying to do reduction (reduce) δ t a s k \delta_{\rm task} δtask To achieve parameter efficacy .- reference [ 62 ] [62] [62]: Use L 0 L_0 L0 The penalty for ( reference [ 117 ] [117] [117]), So that δ t a s k \delta_{\rm task} δtask sparse .
- reference [ 103 ] [103] [103]: Use references [ 2 ] [2] [2] Proposed FastFood Transformation matrix M M M So that δ t a s k \delta_{\rm task} δtask Low dimension ( δ t a s k = δ l o w M \delta_{\rm task}=\delta_{\rm low}M δtask=δlowM).
- reference [ 119 ] [119] [119]: Replace addition with multiplication , namely θ t a s k = θ p r e t r a i n e d ⊙ δ t a s k \theta_{\rm task}=\theta_{\rm pretrained}\odot\delta_{\rm task} θtask=θpretrained⊙δtask
The difference between the two methods is that the former believes that portability stems from the output characteristics of the model , The latter believes that the portability comes from the model weight .
3.1.4 Data efficiency Data Efficiency
Data efficiency (data efficiency) It is discussed that adaptation training requires a large number of labeled sample pairs , In order to reduce the dependence on training data , The resulting concept is Learn less (few-shot learning) And Zero shot learning (zero-shot learning). There are two main ideas , One is Improve the wide applicability of the pre training model ( More knowledge and data can be integrated into the pre training model ), Second, according to the source domain data Simply and quickly generate target domain data and its annotation .
promote Methods of data efficacy :,
Index learning (metric learning): reference [ 180 , 162 , 24 ] [180,162,24] [180,162,24]
It mainly refers to that the large model is easy to be fitted with a small amount of data training , But consider using some nonparametric methods , For example, the nearest neighbor algorithm can effectively deal with over fitting 、 Less shooting problem 、 Zero shot problem, etc .
- reference [ 180 ] [180] [180]: The application of attention mechanism in obtaining weighted nearest neighbors .( It feels too far fetched )
- reference [ 162 ] [162] [162]: For the classification problem , It is considered that the mean value of all sample characteristics in each category can be used as the type (prototype), Then by looking for the nearest type To sort it out .( In fact, it is the standard clustering algorithm )
- reference [ 24 ] [24] [24]: Replace the linear classifier with the classifier based on cosine distance , For less shooting learning .
Prompt learning (prompt learning):
The authors note :
At first, it felt a little like software engineering agile development , And translate into Agile learning , But it seems to follow Tips More relevant .
With references [ 18 ] [18] [18] Super large pre training model in GPT-3 For example , In the process of fine-tuning , The model accepts input x \bf x x And predict the output y \bf y y The probability of is P ( y ∣ x ) P({\bf y}|{\bf x}) P(y∣x), And in the prompt process , according to Prompt template (prompt template) Enter the original x \bf x x Dig some Slot position (unfilled slots) obtain x ~ {\bf \tilde x} x~, The pre training model will x ~ {\bf \tilde x} x~ Make up the slot dug in x ^ \bf \hat x x^, And based on x ^ \bf \hat x x^ Output y \bf y y, The specific operation is shown in the table below :
name Mark Example Input x \bf x x I like this movie Output y \bf y y Emotional polarity : just Prompt template f p r o m p t ( x ) f_{\rm prompt}({\bf x}) fprompt(x) [ X ] [X] [X] In short, this is a [ Z ] [Z] [Z] The movie prompt ( Unfilled ) x ~ \bf \tilde x x~ I like this movie , In short, this is a [ Z ] [Z] [Z] The movie prompt ( Filled ) x ^ \bf \hat x x^ I like this movie , In a word, this is a good movie The advantage of introducing prompt is that it can deal with adaptive learning of less shooting task or zero shooting task , Especially useful in question and answer system .
Finally, I will Prompt learning Combined with fine tuning : reference [ 151 , 100 , 189 ] [151,100,189] [151,100,189], Specific as Figure 17 Shown :
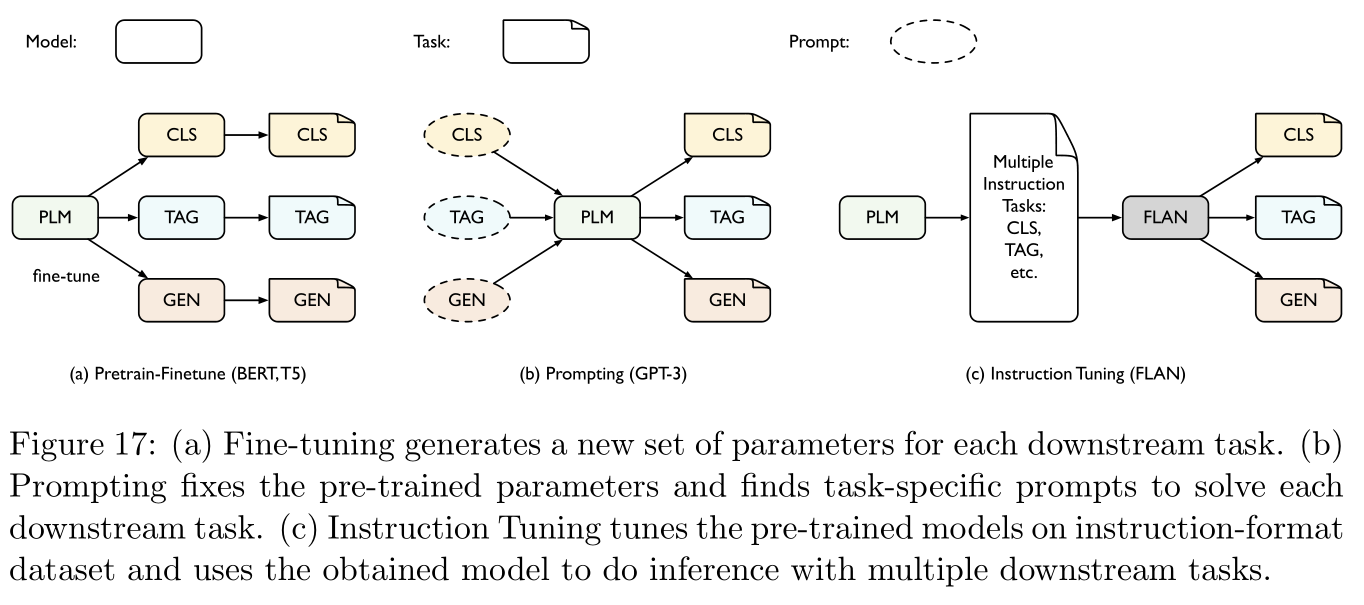
3.1.5 notes Remarks
Summarize the performance of all methods in this section :
| Method | Adaptability | Data efficiency | Parameter efficacy | Modal ductility | Task extensibility |
|---|---|---|---|---|---|
| Feature conversion | Bad | in | optimal | optimal | optimal |
| Ordinary fine tuning | optimal | Bad | Bad | optimal | optimal |
| Domain adaptability tuning | optimal | in | Bad | in | optimal |
| Regularization tuning | optimal | in | Bad | optimal | Bad |
| Residual tuning | in | in | in | in | in |
| Parameter difference tuning | in | in | in | optimal | optimal |
| Index learning | Bad | optimal | optimal | optimal | Bad |
| Prompt learning | in | optimal | optimal | Bad | Bad |
Field description :
- Adaptability (adaptation performance): Model performance when there is a large amount of annotation data in downstream tasks .
- Data efficiency (data efficiency): Model performance when there is only a small amount of data in downstream tasks .
- Parameter efficacy (parameter efficiency): When the number of downstream tasks continues to increase , Can you control the total number of parameters .
- Modal ductility (modality scalability): Can it be used for multimodal data , Text 、 picture 、 Audio-visual .
- Task extensibility (task scalability): Can you easily migrate the pre training model to different downstream tasks .
3.2 Domain adaptability Domain Adaptation
So-called Domain adaptability (Domain Adaptation), It means that the training data in the target domain is unmarked , The training data in the source domain is labeled . So try to pre train the model in the source domain , Then try to migrate to the target field for fine-tuning . Although there is some correlation between the data of the source domain and the target domain , But there must be some differences in distribution , Therefore, the performance of the migration fine-tuning model is often poor . This phenomenon is called Distribution drift (distribution shift, reference [ 133 ] [133] [133]), Domain adaptability It is used to eliminate the gap between the training field and the testing field Distribution drift problem .
Traditional domain adaptation methods such as Reweighting (re-weighting)、 Sample from the source domain ( reference [ 165 ] [165] [165])、 Modeling the transformation from source domain distribution feature space to target domain distribution feature space ( reference [ 53 ] [53] [53]]), These methods are relatively trivial , Such as references [ 76 , 126 , 111 ] [76,126,111] [76,126,111] The study is Nuclear regeneration Hilbert space (kernel-reproducing Hilbert space) Distribution mapping method , reference [ 53 ] [53] [53] The research is to Principal component axis (principal axes) Related to the distribution of various fields . This review focuses on Deep domain adaptability (deep domain adaptation), That is to use the deep learning model architecture to model the adaptive module , Used to match the data distribution of different fields
stay Unsupervised domain adaptability (unsupervised domain adaptation,UDA) in , Source domain S ^ = { ( x i s , y i s ) } i = 1 n \mathcal{\hat S}=\{({\bf x}_i^{s},{\bf y}_i^{s})\}_{i=1}^n S^={ (xis,yis)}i=1n Contained in the n n n Marked samples , Target areas T ^ = { x i t } i = 1 m \mathcal{\hat T}=\{ {\bf x}_i^t\}_{i=1}^m T^={ xit}i=1m Contained in the m m m Unmarked samples , The goal is to learn algorithms to find a hypothesis (hypothesis, It's actually mapping ) h ∈ H : X → Y h\in\mathcal{H}:\mathcal{X\rightarrow Y} h∈H:X→Y, Minimize the target risk :
minimize ϵ T ( h ) = E ( x t , y t ) ∼ T [ l ( h ( x t ) , y t ) ] \text{minimize}\quad\epsilon_{\mathcal{T}}(h)=\mathbb{E}_{({\bf x}^t,{\bf y}^t)\sim\mathcal{T}}[l(h({\bf x}^t),{\bf y}^t)] minimizeϵT(h)=E(xt,yt)∼T[l(h(xt),yt)]
among l : Y × Y → R + l:\mathcal{Y\times Y}\rightarrow\R_+ l:Y×Y→R+ Is the loss function . Currently on UDA The core of theoretical research is how to pass the source risk ϵ S \epsilon_{\mathcal{S}} ϵS as well as Distribution distance (distribution distance) To control the target risk ϵ T ( h ) \epsilon_{\mathcal{T}}(h) ϵT(h) The magnitude of , Here we mainly introduce two classical research theories H Δ H \mathcal{H}\Delta\mathcal{H} HΔH The divergence (Divergence, reference [ 9 , 10 , 120 ] [9,10,120] [9,10,120]) And The gap is contradictory (Disparity Discrepancy, reference [ 204 ] [204] [204]), And how to design different algorithms based on these theories .
The authors note :
there hypothesis h h h It can be understood as the black box model of machine learning , Suppose only the true and the false , therefore h h h The output of should be only zero one , That is, it is aimed at the problem of two classifications . risk (risk) It can be understood as the value of the loss function ( Mathematical expectation ), On the whole, we are reducing the loss value of model training .
First use trigonometric inequality , The unequal relationship between target risk and source risk can be constructed :
Theorem 3 3 3(Bound with Disparity):
Suppose the loss function l l l yes symmetrical (symmetric) And obey trigonometric inequality , Define any two distributions D \mathcal{D} D Assumptions on h h h And h ′ h' h′ Between disparity (disparity):
ϵ D ( h , h ′ ) = E x , y ∼ D [ l ( h ( x ) , h ′ ( x ) ) ] (14) \epsilon_{\mathcal{D}}(h,h')=\mathbb{E}_{ {\bf x},{\bf y}\sim\mathcal{D}}[l(h({\bf x}),h'({\bf x}))]\tag{14} ϵD(h,h′)=Ex,y∼D[l(h(x),h′(x))](14)
Then the target risk ϵ T ( h ) \epsilon_{\mathcal{T}}(h) ϵT(h) Satisfy :
ϵ T ( h ) ≤ ϵ S ( h ) + [ ϵ S ( h ∗ ) + ϵ T ( h ∗ ) ] + ∣ ϵ S ( h , h ∗ ) − ϵ T ( h , h ∗ ) ∣ (15) \epsilon_{\mathcal{T}}(h)\le\epsilon_{\mathcal{S}}(h)+[\epsilon_{\mathcal{S}}(h^*)+\epsilon_{\mathcal{T}}(h^*)]+|\epsilon_{\mathcal{S}}(h,h^*)-\epsilon_{\mathcal{T}}(h,h^*)|\tag{15} ϵT(h)≤ϵS(h)+[ϵS(h∗)+ϵT(h∗)]+∣ϵS(h,h∗)−ϵT(h,h∗)∣(15)
among h ∗ = argmax h ∈ H [ ϵ S ( h ) + ϵ T ( h ) ] h^*=\text{argmax}_{h\in\mathcal{H}}[\epsilon_{\mathcal{S}}(h)+\epsilon_{\mathcal{T}}(h)] h∗=argmaxh∈H[ϵS(h)+ϵT(h)] yes Ideal joint hypothesis (ideal joint hypothesis), ϵ ideal = ϵ S ( h ∗ ) + ϵ T ( h ∗ ) \epsilon_{\text{ideal}}=\epsilon_{\mathcal{S}}(h^*)+\epsilon_{\mathcal{T}}(h^*) ϵideal=ϵS(h∗)+ϵT(h∗) yes Ideal joint error (ideal joint error), ∣ ϵ S ( h , h ∗ ) − ϵ T ( h , h ∗ ) ∣ |\epsilon_{\mathcal{S}}(h,h^*)-\epsilon_{\mathcal{T}}(h,h^*)| ∣ϵS(h,h∗)−ϵT(h,h∗)∣ It's distribution S \mathcal{S} S And T \mathcal T T Between Gap difference (disparity difference).
The authors note :
The symmetry of the loss function satisfies the commutative law , namely l ( y 1 , y 2 ) = l ( y 2 , y 1 ) l(y_1,y_2)=l(y_2,y_1) l(y1,y2)=l(y2,y1); The loss function can be seen as the difference between two vectors , So the formula ( 14 ) (14) (14) It measures two assumptions ( The model ) The difference degree of prediction results .
In the research of domain adaptability , It is usually assumed that Ideal joint error ( That is, the sum of the loss function of the source domain task and the target domain task ) Is sufficiently small , Otherwise, domain adaptation itself is not feasible ( That is, it cannot be trained until the loss function reaches a low level , Corresponding references [ 10 ] [10] [10] Proposed in The impossibility theorem ,impossibility theorem), Present tense ( 15 ) (15) (15) Only the last item needs to be examined Gap difference The numerical .
However, the target dataset label is not available , So the ideal hypothesis h ∗ h^* h∗ It is unknown. , therefore Gap difference It cannot be estimated directly , H Δ H \mathcal{H}\Delta\mathcal{H} HΔH The divergence It is used to measure Gap difference The upper bound of :
Definition 4 4 4( H Δ H \mathcal{H}\Delta\mathcal{H} HΔH The divergence ):
Definition H Δ H = Δ { h ∣ h = h 1 ⊗ h 2 , h 1 , h 2 ∈ H } \mathcal{H}\Delta\mathcal{H}\overset{\Delta}{=}\{h|h=h_1\otimes h_2,h_1,h_2\in\mathcal{H}\} HΔH=Δ{ h∣h=h1⊗h2,h1,h2∈H} For hypothetical space H \mathcal{H} H Of Symmetric difference hypothesis space (symmetric difference hypothesis space), among ⊗ \otimes ⊗ Express Exclusive or operator (XOR), Then the distribution S \mathcal S S And T \mathcal T T Between H Δ H \mathcal{H}\Delta\mathcal{H} HΔH The divergence It can be expressed as :
d H Δ H ( S , T ) = Δ sup h , h ′ ∈ H ∣ ϵ S ( h , h ′ ) − ϵ T ( h , h ′ ) ∣ d_{\mathcal{H}\Delta\mathcal{H}}(\mathcal{S,T})\overset\Delta=\sup_{h,h'\in\mathcal{H}}|\epsilon_{\mathcal S}(h,h')-\epsilon_{\mathcal T}(h,h')| dHΔH(S,T)=Δh,h′∈Hsup∣ϵS(h,h′)−ϵT(h,h′)∣
Specially , For the zero one loss function of binary classification problem , namely l ( y , y ′ ) = 1 ( y ≠ y ′ ) l(y,y')=\textbf{1}(y\neq y') l(y,y′)=1(y=y′), Yes :
d H Δ H ( S , T ) = Δ sup δ ∈ H Δ H ∣ E S [ δ ( x ) ≠ 0 ] − E T [ δ ( x ) ≠ 0 ] ∣ d_{\mathcal{H}\Delta\mathcal{H}}(\mathcal{S,T})\overset\Delta=\sup_{\delta\in\mathcal{H\Delta H}}|\mathbb{E}_{\mathcal{S}}[\delta({\bf x})\neq0]-\mathbb{E}_{\mathcal{T}}[\delta({\bf x})\neq0]| dHΔH(S,T)=Δδ∈HΔHsup∣ES[δ(x)=0]−ET[δ(x)=0]∣
The authors note :
H Δ H \mathcal{H}\Delta\mathcal{H} HΔH The test is the case where the two hypotheses are different ( Exclusive or operation ). So in the second equation δ ( x ) \delta({\bf x}) δ(x) The value of is only zero one , δ ( x ) ≠ 0 \delta(x)\neq 0 δ(x)=0 Indicates that two assumptions are different ( That is, the prediction results of the model are different ), The whole is the absolute value of the difference between two assumptions ( Distance ).
Then look at the first formula again , According to the type ( 14 ) (14) (14) You know , ϵ D ( h , h ′ ) \epsilon_{\mathcal{D}}(h,h') ϵD(h,h′) It measures two assumptions ( The model ) h h h And h ′ h' h′ In the distribution D \mathcal{D} D The difference value of the above prediction results , Absolute value measures distance , Therefore, the gap is the gap , abbreviation Gap difference .
You can sample a limited number of unlabeled samples from the source domain and the target domain H Δ H \mathcal{H}\Delta\mathcal{H} HΔH Divergence is estimated ( That is, use multiple groups of different models to predict the results in the source field and the target field respectively and calculate Gap difference ), But the specific calculation optimization is very difficult . The usual practice is to train a Domain identifier (domain discriminator) D D D To divide the samples of source domain and target domain ( reference [ 9 , 45 ] [9,45] [9,45]). We assume that Recognizer family (family of the discriminators) Rich enough to contain H Δ H \mathcal{H\Delta H} HΔH, namely H Δ H ⊂ H D \mathcal{H\Delta H}\subset\mathcal{H}_D HΔH⊂HD( For example, neural networks can be used to approximate almost all functions ), be H Δ H \mathcal{H}\Delta\mathcal{H} HΔH Divergence can be further controlled within the range of the following formula :
sup D ∈ H D ∣ E S [ D ( x ) = 1 ] + E T [ D ( x ) = 0 ] ∣ \sup_{D\in \mathcal{H}_D}|\mathbb E_{\mathcal S}[D({\bf x})=1]+\mathbb{E}_{\mathcal T}[D({\bf x})=0]| D∈HDsup∣ES[D(x)=1]+ET[D(x)=0]∣
The authors note :
D ( x ) = 0 D({\bf x})=0 D(x)=0 Presentation sample x \bf x x It belongs to the source field , D ( x ) = 1 D({\bf x})=1 D(x)=1 Presentation sample x \bf x x Belong to the target field , Therefore, two terms in the absolute value represent the probability that the prediction result is wrong , But according to Gap difference The definition of , Whether it should be a minus sign instead of a plus sign ?
This idea leads to Section 3.2.2 in Field opposition (domain adversarial) Method . Besides , If the nonparametric method is used for H Δ H \mathcal{H}\Delta\mathcal{H} HΔH Divergence is estimated , For example, will H Δ H \mathcal{H}\Delta\mathcal{H} HΔH Use a function space F \mathcal F F replace , That is, derived Section 3.2.1 Medium Statistical matching (statistics matching) Method .
The authors note :
According to the definition , H Δ H \mathcal{H}\Delta\mathcal{H} HΔH Itself is also a hypothetical space , It can be understood as a model set or mapping group , Therefore, it can be approximated by a family of functions .
The following theorem is about Domain adaptability One of the earliest studies , It is based on H Δ H \mathcal{H}\Delta\mathcal{H} HΔH The general upper bound of the binary classification problem of divergence :
Theorem 5 5 5( reference [ 10 ] [10] [10]):
H \mathcal{H} H It's a Binary hypothesis space (binary hypothesis space), if S ^ \mathcal{\hat S} S^ And T ^ \mathcal{\hat T} T^ The capacity is m m m The sample of , Then for any δ ∈ ( 0 , 1 ) \delta\in(0,1) δ∈(0,1), There are at least 1 − δ 1-\delta 1−δ The following formula holds :
ϵ T ( h ) ≤ ϵ S ( h ) + d H Δ H ( S ^ , T ^ ) + ϵ i d e a l + 4 2 d log ( 2 m ) + log ( 2 / δ ) m ( ∀ h ∈ H ) (16) \epsilon_{\mathcal{T}}(h)\le\epsilon_{\mathcal{S}}(h)+d_{\mathcal{H}\Delta\mathcal{H}}(\mathcal{\hat S,\hat T})+\epsilon_{\rm ideal}+4\sqrt{\frac{2d\log(2m)+\log(2/\delta)}{m}}\quad(\forall h\in\mathcal H)\tag{16} ϵT(h)≤ϵS(h)+dHΔH(S^,T^)+ϵideal+4m2dlog(2m)+log(2/δ)(∀h∈H)(16)
** Theorem 5 5 5** The drawback of is that it can only be used for binary classification problems , So references [ 45 ] [45] [45] It is extended to the case of multi classification :
Theorem 6 6 6( reference [ 45 ] [45] [45]):
Suppose the loss function l l l Symmetric and subject to trigonometric inequality , Definition
h S ∗ = argmin h ∈ H ϵ S ( h ) h T ∗ = argmin h ∈ H ϵ T ( h ) h_{\mathcal S}^*=\text{argmin}_{h\in\mathcal{H}}\epsilon_{\mathcal{S}}(h)\\ h_{\mathcal T}^*=\text{argmin}_{h\in\mathcal{H}}\epsilon_{\mathcal{T}}(h) hS∗=argminh∈HϵS(h)hT∗=argminh∈HϵT(h)
Respectively represent the source domain and the target domain Ideal hypothesis , Then there are :
ϵ T ( h ) ≤ ϵ S ( h , h S ∗ ) + d H Δ H ( S , T ) + ϵ ( ∀ h ∈ H ) (17) \epsilon_{\mathcal{T}}(h)\le\epsilon_{\mathcal{S}}(h,h^*_{\mathcal S})+d_{\mathcal{H}\Delta\mathcal{H}}(\mathcal{S,T})+\epsilon\quad(\forall h\in\mathcal{H})\tag{17} ϵT(h)≤ϵS(h,hS∗)+dHΔH(S,T)+ϵ(∀h∈H)(17)
among ϵ S ( h , h S ∗ ) \epsilon_{\mathcal{S}}(h,h^*_{\mathcal S}) ϵS(h,hS∗) Indicates the source domain risk , ϵ \epsilon ϵ Indicates adaptability :
ϵ = ϵ T ( h T ∗ ) + ϵ S ( h T ∗ , h S ∗ ) \epsilon=\epsilon_{\mathcal T}(h_{\mathcal T}^*)+\epsilon_{\mathcal S}(h_{\mathcal T}^*,h_{\mathcal S}^*) ϵ=ϵT(hT∗)+ϵS(hT∗,hS∗)
further , if l l l bounded , namely ∀ ( y , y ′ ) ∈ Y 2 , ∃ M > 0 \forall (y,y')\in\mathcal{Y}^2,\exists M>0 ∀(y,y′)∈Y2,∃M>0, bring l ( y , y ′ ) ≤ M l(y,y')\le M l(y,y′)≤M. As defined l ( y , y ′ ) = ∣ y − y ′ ∣ q l(y,y')=|y-y'|^q l(y,y′)=∣y−y′∣q, if S ^ \mathcal{\hat S} S^ And T ^ \mathcal{\hat T} T^ Yes, the capacity is n n n and m m m The sample of , At least 1 − δ 1-\delta 1−δ The following formula holds :
d H Δ H ( S , T ) ≤ d H Δ H ( S ^ , T ^ ) + 4 q ( R n , S ( H ) + R m , T ( H ) ) + 3 M ( log ( 4 / δ ) 2 n + log ( 4 / δ ) 2 m ) (18) d_{\mathcal{H}\Delta\mathcal{H}}(\mathcal{S,T})\le d_{\mathcal{H}\Delta\mathcal{H}}(\mathcal{\hat S,\hat T})+4q(\mathfrak{R}_{n,\mathcal{S}}(\mathcal{H})+\mathfrak{R}_{m,\mathcal{T}}(\mathcal{H}))+3M\left(\sqrt{\frac{\log(4/\delta)}{2n}}+\sqrt{\frac{\log(4/\delta)}{2m}}\right)\tag{18} dHΔH(S,T)≤dHΔH(S^,T^)+4q(Rn,S(H)+Rm,T(H))+3M(2nlog(4/δ)+2mlog(4/δ))(18)
among R n , D \mathfrak{R}_{n,\mathcal{D}} Rn,D Express Expected radmach complexity (Expected Rademacher Complexity, reference [ 6 ] [6] [6]).
All of the above H Δ H \mathcal{H}\Delta\mathcal{H} HΔH The upper bound of divergence is still too loose ( because h h h and h ′ h' h′ It's optional , Then the supremum value will be very large ), So references [ 204 ] [204] [204] Consider fixing one of these assumptions , Put forward The gap is contradictory The concept of ( Please contact the above Gap difference Distinguish , One is disparity discrepancy, One is disparity difference):
Definition 7 7 7( The gap is contradictory ):
Given Binary hypothesis space H \mathcal{H} H And a specific assumption h ∈ H h\in\mathcal{H} h∈H, from h h h Derived The gap is contradictory Defined as :
d h , H ( S , T ) = sup h ′ ∈ H ( E T 1 [ h ′ ≠ h ] − E S 1 [ h ′ ≠ h ] ) (19) d_{h,\mathcal{H}}(\mathcal{S,T})=\sup_{h'\in\mathcal{H}}(\mathbb{E}_{\mathcal T}\textbf{1}[h'\neq h]-\mathbb{E}_{\mathcal S}\textbf{1}[h'\neq h])\tag{19} dh,H(S,T)=h′∈Hsup(ET1[h′=h]−ES1[h′=h])(19)
The authors note :
contrast ** Definition 4 4 4** Medium H Δ H \mathcal{H}\Delta\mathcal{H} HΔH The divergence , Here is actually a fixed h h h, Nothing else makes any difference . Definitions and theorems from here down are basically of no practical significance .
At this time, the supremum is only a hypothesis h ′ h' h′ Take office , Therefore, the upper bound is greatly reduced , And it should be easier to calculate . The gap is contradictory It can be well used to measure Distribution drift (distribution shift) The degree of .
Theorem 8 8 8( reference [ 204 ] [204] [204]):
S ^ \mathcal{\hat S} S^ And T ^ \mathcal{\hat T} T^ Yes, the capacity is n n n and m m m The sample of , For arbitrary δ > 0 \delta>0 δ>0 And every binary classifier h ∈ H h\in\mathcal{H} h∈H, At least 1 − 3 δ 1-3\delta 1−3δ The following formula holds :
ϵ T ( h ) ≤ ϵ S ^ ( S ^ , T ^ ) + d h , H ( S ^ , T ^ ) + ϵ i d e a l + 2 R n , S ( H ) + 2 R n , S ( H Δ H ) + 2 log ( 2 / δ ) 2 n + 2 R m , T ( H Δ H ) + 2 log ( 2 / δ ) 2 m (20) \epsilon_{\mathcal{T}}(h)\le\epsilon_{\mathcal{\hat S}}(\mathcal{\hat S,\hat T})+d_{h,\mathcal H}(\mathcal{\hat S,\hat T})+\epsilon_{\rm ideal}+2\mathfrak{R}_{n,\mathcal S}(\mathcal{H})\\+2\mathfrak{R}_{n,\mathcal S}(\mathcal{H\Delta H})+2\sqrt{\frac{\log(2/\delta)}{2n}}+2\mathfrak{R}_{m,\mathcal T}(\mathcal{H\Delta H})+2\sqrt{\frac{\log(2/\delta)}{2m}}\tag{20} ϵT(h)≤ϵS^(S^,T^)+dh,H(S^,T^)+ϵideal+2Rn,S(H)+2Rn,S(HΔH)+22nlog(2/δ)+2Rm,T(HΔH)+22mlog(2/δ)(20)
** Theorem 8 8 8** It is the case of two categories , It can be extended to the case of multi classification , Before that, let's give a new definition :
Definition 9 9 9( Marginal gap contradiction )
Given a Scoring hypothesis space (scoring hypothesis space) F \mathcal F F, Make
ρ f ( x , y ) = Δ 1 2 ( f ( x , y ) − max y ′ ≠ y f ( x , y ′ ) ) \rho_f(x,y)\overset\Delta=\frac12(f(x,y)-\max_{y'\neq y}f(x,y')) ρf(x,y)=Δ21(f(x,y)−y′=ymaxf(x,y′))
Indicates in the sample pair ( x , y ) (x,y) (x,y) Situated Real hypothesis (real hypothesis) f f f Of limit (margin), Make
h f : x → argmax y ∈ Y f ( x , y ) h_f:x\rightarrow\text{argmax}_{y\in\mathcal Y}f(x,y) hf:x→argmaxy∈Yf(x,y)
By f f f Derived Tag function (labeling function), Make
Φ ρ ( x ) = Δ { 0 x ≥ ρ 1 − x ρ 0 ≤ x ≤ ρ 1 x ≤ 0 (21) \Phi_{\rho}(x)\overset\Delta=\left\{\begin{aligned} &0&&x\ge \rho\\ &1-\frac x\rho&&0\le x\le\rho\\ &1&&x\le0\\ \end{aligned}\right.\tag{21} Φρ(x)=Δ⎩⎪⎪⎨⎪⎪⎧01−ρx1x≥ρ0≤x≤ρx≤0(21)
Express Marginal Loss (margin loss), Is distributed D \mathcal{D} D On , f f f And f ′ f' f′ Of Marginal gap (margin disparity) by :
ϵ D ( ρ ) ( f ′ , f ) = E ( x , y ) ∼ D [ Φ ρ ( ρ f ′ ( x , h f ( x ) ) ) ] (22) \epsilon_{\mathcal D}^{(\rho)}(f',f)=\mathbb{E}_{(x,y)\sim\mathcal D}[\Phi_{\rho}(\rho_{f'}(x,h_f(x)))]\tag{22} ϵD(ρ)(f′,f)=E(x,y)∼D[Φρ(ρf′(x,hf(x)))](22)
Given specific assumptions f ∈ F f\in\mathcal F f∈F, be Marginal gap contradiction (margin disparity discrepancy) by :
d f , F ( ρ ) ( S , T ) = sup f ′ ∈ F [ ϵ T ( ρ ) ( f ′ , f ) − ϵ S ( ρ ) ( f ′ , f ) ] (23) d_{f,\mathcal F}^{(\rho)}(\mathcal{S,T})=\sup_{f'\in\mathcal F}[\epsilon_{\mathcal T}^{(\rho)}(f',f)-\epsilon_{\mathcal S}^{(\rho)}(f',f)]\tag{23} df,F(ρ)(S,T)=f′∈Fsup[ϵT(ρ)(f′,f)−ϵS(ρ)(f′,f)](23)
According to the type ( 22 ) (22) (22) You know Marginal gap Satisfy nonnegativity and Subadditivity (subadditivity), But it's not asymmetric , Therefore, we cannot directly ** Theorem 6 6 6** Use this to generate a new upper bound , So we have the last theorem in this section :
Theorem 10 10 10( reference [ 204 ] [204] [204]):
stay Definition 9 9 9 Under the assumption that , For arbitrary δ > 0 \delta>0 δ>0, And whatever Scoring function f ∈ F f\in\mathcal F f∈F, At least 1 − 3 δ 1-3\delta 1−3δ The following formula holds :
ϵ T ( h ) ≤ ϵ S ^ ( ρ ) ( f ) + d f , F ( ρ ) ( S ^ , T ^ ) + ϵ i d e a l + 2 k 2 ρ R n , S ( Π 1 F ) + k ρ R n , S ( Π H F ) + 2 log ( 2 / δ ) 2 n + 2 R m , T ( Π H F ) + 2 log ( 2 / δ ) 2 m (24) \epsilon_{\mathcal{T}}(h)\le\epsilon_{\mathcal{\hat S}}^{(\rho)}(f)+d_{f,\mathcal F}^{(\rho)}(\mathcal{\hat S,\hat T})+\epsilon_{\rm ideal}+\frac{2k^2}{\rho}\mathfrak{R}_{n,\mathcal S}(\Pi_1\mathcal{F})\\+\frac k\rho\mathfrak{R}_{n,\mathcal S}(\Pi_{\mathcal H}\mathcal{F})+2\sqrt{\frac{\log(2/\delta)}{2n}}+2\mathfrak{R}_{m,\mathcal T}(\Pi_{\mathcal H}\mathcal{F})+2\sqrt{\frac{\log(2/\delta)}{2m}}\tag{24} ϵT(h)≤ϵS^(ρ)(f)+df,F(ρ)(S^,T^)+ϵideal+ρ2k2Rn,S(Π1F)+ρkRn,S(ΠHF)+22nlog(2/δ)+2Rm,T(ΠHF)+22mlog(2/δ)(24)
** Theorem 10 10 10** The upper bound of the margin in indicates an appropriate margin ρ \rho ρ It can generate better promotion results in the target field . Theorem 8 8 8 And Theorem 10 10 10 Co constitute Section 3.2.3 Medium Suppose the opposite (hypothesis adversarial) Method .
Notice whether it is H Δ H \mathcal{H}\Delta\mathcal{H} HΔH The divergence still The gap is contradictory , The supremum symbol sup \sup sup Are only in hypothetical space H \mathcal H H It only makes sense when you are younger , However, in the general neural network model , Hypothetical space H \mathcal H H Will be very large , At this time, taking the supremum will tend to be positive and infinite and lose its meaning . However, the hypothesis space can be reduced by pre training in upstream tasks , This is it. Field opposition And Suppose the opposite Pre training necessary for the method .
3.2.1 Statistical matching Statistics Matching
Many upper bound theoretical results on domain adaptability have been introduced above , The problem is that most of these theories rely on Suppose the derived (hypothesis-induced) Distribution distance , These theoretical results are not very intuitive before the model is trained , Therefore, this section mainly introduces some probability results based on statistics . Be careful , reference [ 112 , 114 ] [112,114] [112,114] A lot based on Suppose the derived Domain adaptive algorithm based on Distributed Distance construction .
Definition 11 11 11( The largest average gap ):
Given two probability distributions S , T \mathcal{S,T} S,T as well as Measurable space (measurable space) X \bf X X, Overall probability index (integral probability metric, reference [ 140 ] [140] [140]) Defined as :
d F ( S , T ) = Δ sup f ∈ F ∣ E x ∼ S [ f ( x ) ] − E x ∼ T [ f ( x ) ] ∣ d_{\mathcal F}(\mathcal{S,T})\overset\Delta=\sup_{f\in\mathcal F}|\mathbb{E}_{ {\bf x}\sim \mathcal{S}}[f({\bf x})]-\mathbb{E}_{ {\bf x}\sim \mathcal{T}}[f({\bf x})]| dF(S,T)=Δf∈Fsup∣Ex∼S[f(x)]−Ex∼T[f(x)]∣
among F \mathcal F F yes X \bf X X A class of bounded functions on . reference [ 163 ] [163] [163] Further constrain F \mathcal{F} F To Kernel Hilbert space (kernel Hilbert space,RKHS) H k \mathcal{H}_k Hk One of them Unit ball (unit ball) Inside , namely F = { f ∈ H k : ∥ f ∥ H k ≤ 1 } \mathcal F=\{f\in\mathcal{H}_k:\|f\|_{\mathcal{H}_k}\le1\} F={ f∈Hk:∥f∥Hk≤1}, among k k k yes Characteristic core (characteristic kernel), Derived from this The largest average gap (maximum mean discrepancy,MMD, reference [ 57 ] [57] [57]):
d M M D 2 ( S , T ) = ∥ E x ∈ S [ ϕ ( x ) ] − E x ∈ T [ ϕ ( x ) ] ∥ H k 2 (25) d_{\rm MMD}^2(\mathcal{S,T})=\|\mathbb{E}_{ {\bf x}\in\mathcal S}[\phi({\bf x})]-\mathbb{E}_{ {\bf x}\in\mathcal T}[\phi({\bf x})]\|_{\mathcal H_k}^2\tag{25} dMMD2(S,T)=∥Ex∈S[ϕ(x)]−Ex∈T[ϕ(x)]∥Hk2(25)
among ϕ ( x ) \phi(x) ϕ(x) Is with kernel function k k k Related feature mapping , Satisfy :
k ( x , x ′ ) = < ϕ ( x ) , ϕ ( x ′ ) > k({\bf x},{\bf x}')=\left<\phi({\bf x}),\phi({\bf x}')\right> k(x,x′)=*ϕ(x),ϕ(x′)*
Can prove that , S = T \mathcal S=\mathcal T S=T At present only if d F ( S , T ) = 0 d_{\mathcal F}(\mathcal{S,T})=0 dF(S,T)=0 or d M M D 2 ( S , T ) = 0 d^2_{\rm MMD}(\mathcal{S,T})=0 dMMD2(S,T)=0Theorem 12 12 12( reference [ 140 ] [140] [140]):
Given and Definition 11 11 11 The same settings , l l l Is a convex loss function , Form like l ( y , y ′ ) = ∣ y − y ′ ∣ q l(y,y')=|y-y'|^q l(y,y′)=∣y−y′∣q, Then for any δ > 0 \delta>0 δ>0 as well as ∀ h ∈ F \forall h\in\mathcal F ∀h∈F, There are at least 1 − δ 1-\delta 1−δ The following formula holds for the probability of :
ϵ T ( h ) ≤ ϵ S ( h ) + d M M D ( S ^ , T ^ ) + ϵ i d e a l + 2 n E x ∼ S [ tr ( K S ) ] + 2 m E x ∼ T [ tr ( K T ) ] + 2 log ( 2 / δ ) 2 n + log ( 2 / δ ) 2 m (26) \epsilon_{\mathcal T}(h)\le\epsilon_{\mathcal S}(h)+d_{\rm MMD}(\mathcal{\hat S,\hat T})+\epsilon_{\rm ideal}+\frac2n\mathbb{E}_{ {\bf x}\sim\mathcal S}\left[\sqrt{\text{tr}({\bf K}_{\mathcal{S}})}\right]\\+\frac2m\mathbb{E}_{ {\bf x}\sim\mathcal T}\left[\sqrt{\text{tr}({\bf K}_{\mathcal{T}})}\right]+2\sqrt{\frac{\log(2/\delta)}{2n}}+\sqrt{\frac{\log(2/\delta)}{2m}}\tag{26} ϵT(h)≤ϵS(h)+dMMD(S^,T^)+ϵideal+n2Ex∼S[tr(KS)]+m2Ex∼T[tr(KT)]+22nlog(2/δ)+2mlog(2/δ)(26)
among K S {\bf K}_{\mathcal{S}} KS And K T {\bf K}_{\mathcal{T}} KT Respectively means according to S \mathcal{S} S and T \mathcal{T} T Calculated from the sample in Kernel matrix (kernel matrices).
In fact, it's the same as the one above Gap difference It doesn't make much difference , Just redefine the new distance calculation method , And replacing assumptions with functions , But in comparison, it has the following advantages :
- Irrelevant to assumptions (hypothesis-free), That is, there is no need to get an exact model to measure the distribution distance .
- Complex items (complexity term) And Vapnik-Chervonenkis Dimension independent .
- MMD The unbiased estimator of can be calculated in linear time .
- MMD The process of minimization has a very beautiful statistical matching explanation in probability theory .
And MMD Relevant studies include : reference [ 174 , 57 , 58 ] [174,57,58] [174,57,58], What is worth noting is the references [ 57 , 58 ] [57,58] [57,58] be based on Deep adaptation to the Internet (deep adaptation network,DAN, reference [ 112 , 116 ] [112,116] [112,116]), Put forward MMD A variation of the Multicore MMD(multi-kernel MMD,MK-MMD), Specific as Figure 19 Shown on the left :
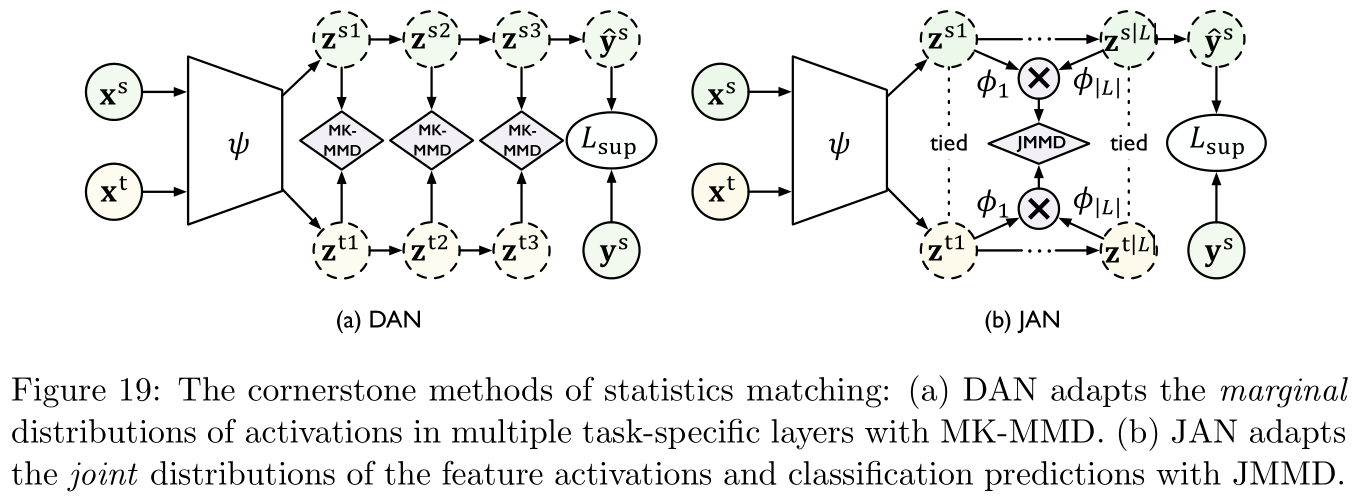
Figure 19 The middle and right pictures are references [ 114 ] [114] [114] Proposed Joint Adaptive Network (joint adaptation network,JAN) Medium Joint maximum average gap (joint maximum mean discrepancy,JMMD), This is used to measure two joint distributions P ( X s , Y s ) P({\bf X}^s,{\bf Y}^s) P(Xs,Ys) And P ( X t , Y t ) P({\bf X}^t,{\bf Y}^t) P(Xt,Yt) Distance between , use { ( z i s 1 , . . . , z i s ∣ L ∣ ) } i = 1 n \{({\bf z}_i^{s1},...,{\bf z}_i^{s|\mathcal L|})\}_{i=1}^n { (zis1,...,zis∣L∣)}i=1n And { ( z i t 1 , . . . , z i t ∣ L ∣ ) } j = 1 m \{({\bf z}_i^{t1},...,{\bf z}_i^{t|\mathcal L|})\}_{j=1}^m { (zit1,...,zit∣L∣)}j=1m Respectively represent activation and adaptation layers L \mathcal{L} L,JMMD The definition is as follows :
d J M M D 2 ( S ^ , T ^ ) = ∥ E i ∈ [ n ] ⊗ l ∈ L ϕ l ( z i s l ) − E j ∈ [ m ] ⊗ l ∈ L ϕ l ( z j t l ) ∥ H k 2 (27) d_{\rm JMMD}^2(\mathcal{\hat S,\hat T})=\|\mathbb{E}_{i\in[n]}\otimes_{l\in\mathcal L}\phi^l({\bf z}_i^{sl})-\mathbb{E}_{j\in[m]}\otimes_{l\in\mathcal L}\phi^l({\bf z}_j^{tl})\|_{\mathcal H_k}^2\tag{27} dJMMD2(S^,T^)=∥Ei∈[n]⊗l∈Lϕl(zisl)−Ej∈[m]⊗l∈Lϕl(zjtl)∥Hk2(27)
among ϕ l \phi^l ϕl It's about kernel function k l k^l kl And the network layer l l l Feature mapping of , ⊗ \otimes ⊗ Represents outer product .
Commonly used in MMD The kernel function in is Gaussian kernel :
k ( x 1 , x 2 ) = exp ( − ∥ x 1 − x 2 ∥ 2 2 σ 2 ) k({\bf x}_1,{\bf x}_2)=\exp\left(\frac{-\|{\bf x}_1-{\bf x}_2\|^2}{2\sigma^2}\right) k(x1,x2)=exp(2σ2−∥x1−x2∥2)
Taylor expansion can be used to expand MMD Expressed as Statistical momentum of each order (all orders of statistic moments) Weighted sum of distances , Based on this idea , reference [ 166 , 200 ] [166,200] [166,200] Yes MMD Made some similar variants .
MMD The drawback of is that it estimates the distance between two fields , The geometric information of data distribution cannot be considered , Research on the improvement of this defect includes references [ 34 , 36 , 29 ] [34,36,29] [34,36,29]
Finally, record some other relevant studies :
- reference [ 102 ] [102] [102]: Directly by aligning Batch of standardized (BatchNorm) Statistics to minimize the domain distance , To alleviate the distribution drift problem .
- reference [ 185 ] [185] [185]: Put forward Portable standardization (transferable normalization,TransNorm), That is to capture sufficient statistics of the field through the mean and standard deviation of the distribution of specific fields .
- reference [ 84 ] [84] [84]: Put forward Compare the adaptation network (contrastive adaptation network,CAN), It seems to use the method of class , It is to alleviate MMD and JMMD Different categories in The samples are not complete (misalign samples) The problem of .
3.2.2 Domain opposite learning Domain Adversarial Learning
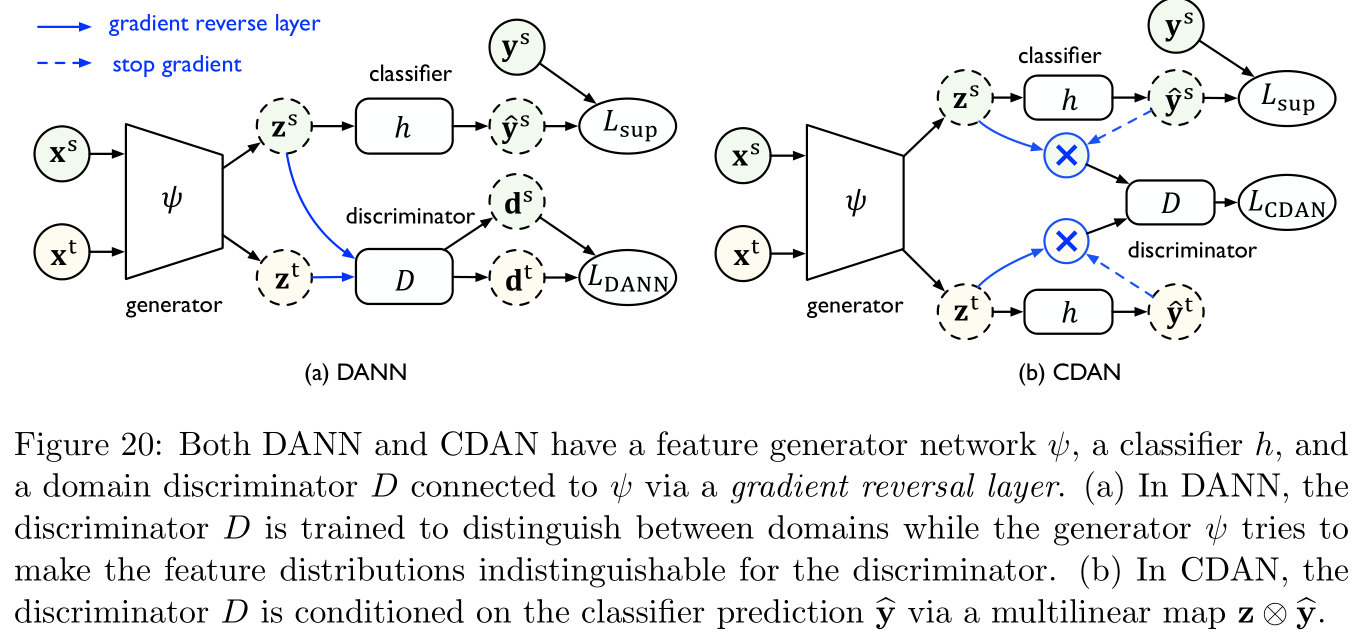
Domain opposition neural network (domain adversarial neural network,DANN, reference [ 45 , 46 ] [45,46] [45,46]):
DANN Itself inspired by Against generative networks (generative adversarial net,GAN, reference [ 54 ] [54] [54]) Modeling idea of distribution . Such as Figure 20 Shown on the left ,DANN It contains two modules , The first module Domain identifier (domain discriminator) D D D Training is used to distinguish Source characteristics (source features) And Target characteristics (target features), The second module Feature generator (feature generator) ψ \psi ψ Training is used to generate features to confuse D D D.
according to Section 3.2 About China H Δ H \mathcal{H\Delta H} HΔH The conclusion of divergence , It can be concluded that H Δ H \mathcal{H\Delta H} HΔH Divergence gap :
L D A N N ( ψ ) = max D E x s ∼ S ^ log [ D ( z s ) ] + E x t ∼ T ^ log [ 1 − D ( z t ) ] (28) L_{\rm DANN}(\psi)=\max_D\mathbb{E}_{ {\bf x}^s\sim\mathcal{\hat S}}\log[D({\bf z}^s)]+\mathbb{E}_{ {\bf x}^t\sim\mathcal{\hat T}}\log[1-D({\bf z}^t)]\tag{28} LDANN(ψ)=DmaxExs∼S^log[D(zs)]+Ext∼T^log[1−D(zt)](28)
among , z = ψ ( x ) {\bf z}=\psi({\bf x}) z=ψ(x) yes x {\bf x} x Feature representation of , Feature generator ψ \psi ψ The objective function of is to minimize Source error (source error) And the formula ( 28 ) (28) (28) Medium H Δ H \mathcal{H\Delta H} HΔH The divergence , As shown below :
min ψ , h E ( x s , y s ) ∼ S ^ L CE ( h ( z s ) , y s ) + λ L ( D A N N ) ( ψ ) (29) \min_{\psi,h}\mathbb{E}_{({\bf x}^s,{\bf y}^s)\sim\mathcal{\hat S}}L_{\text{CE}}(h({\bf z}^s),{\bf y}^s)+\lambda L(\rm DANN)(\psi)\tag{29} ψ,hminE(xs,ys)∼S^LCE(h(zs),ys)+λL(DANN)(ψ)(29)
among L C E L_{\rm CE} LCE It's cross entropy loss , λ \lambda λ It's a super parameter that weighs two terms .reference [ 115 ] [115] [115] fitting ( 28 ) (28) (28) Improved , Put forward Conditional domain opposite network (conditional domain adversarial network,CDAN), That is, the classifier predicts the result y ^ = h ( z ) {\bf \hat y}=h({\bf z}) y^=h(z) Under the conditions of z {\bf z} z Probability distribution of , And introduce Multilinear mapping (multilinear map) z ⊗ y ^ {\bf z}\otimes{\bf \hat y} z⊗y^ To replace ( 28 ) (28) (28) Medium z {\bf z} z As a domain identifier D D D The input of :
L C D A N ( ψ ) = max D E x s ∼ S ^ log [ D ( z s ⊗ y ^ s ) ] + E x t ∼ T ^ log [ 1 − D ( z t ⊗ y ^ t ) ] (30) L_{\rm CDAN}(\psi)=\max_D\mathbb{E}_{ {\bf x}^s\sim\mathcal{\hat S}}\log[D({\bf z}^s\otimes{\bf \hat y}^s)]+\mathbb{E}_{ {\bf x}^t\sim\mathcal{\hat T}}\log[1-D({\bf z}^t\otimes{\bf \hat y}^t)]\tag{30} LCDAN(ψ)=DmaxExs∼S^log[D(zs⊗y^s)]+Ext∼T^log[1−D(zt⊗y^t)](30)
type ( 30 ) (30) (30) Comparative formula ( 29 ) (29) (29) The advantage is that ,CDAN It can completely capture the relationship between feature representation and classifier prediction results Cross variance (cross-variance), Therefore, a better joint distribution can be obtained .improvement : reference [ 176 , 28 , 15 ] [176,28,15] [176,28,15]
reference [ 176 ] [176] [176]: Put forward Opposites distinguish areas of adaptation (adversarial discriminative domain adaptation,ADDA), The solution is DANN The gradient disappearance problem that may appear in , To be specific ADDA The feature generator ψ \psi ψ And domain identifier D D D The optimization process of is divided into two independent parts , among D D D The part and formula of ( 29 ) (29) (29) identical , ψ \psi ψ Part of is transformed into :
min ψ E x t ∼ T ^ − log [ D ( z t ) ] (31) \min_{\psi}\mathbb{E}_{ {\bf x}^t\sim\mathcal{\hat T}}-\log[D({\bf z}^t)]\tag{31} ψminExt∼T^−log[D(zt)](31)reference [ 28 ] [28] [28]: Put forward Batch spectrum penalty (batch spectral penalization,BSP), The feature vector corresponding to the maximum eigenvalue contains more knowledge about migration , Therefore, the penalty term about the maximum singular value is set to enhance the effect of feature classification , This is about the migration model of image processing .
reference [ 15 ] [15] [15]: Introduce a private subspace for each domain , It is used to save information in specific fields , This is also about the migration research of image processing .
The application of domain opposition learning in real scenes :
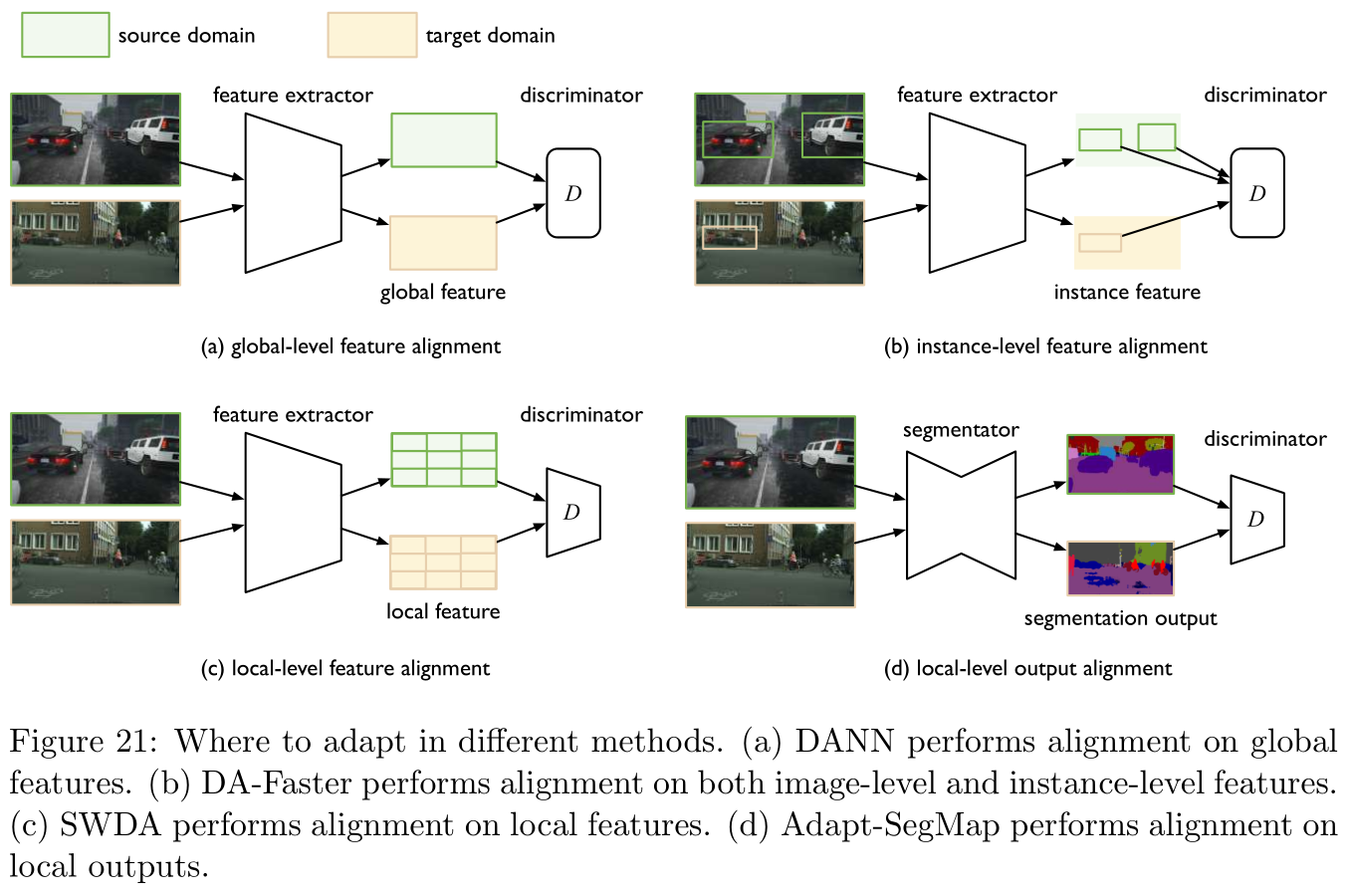
Which part should be adapted is unknown (which part to adapt is unknown):
Here we discuss the field of image processing . In image recognition , We only need to classify the input images , However, in entity recognition , We need to locate first Areas of interest (region of interests,RoIs) And then sort it out . Due to the distribution drift in different fields , So in the target area RoIs The location of is unreliable , Therefore, it is unknown which part of the opposite training should be adapted .
reference [ 30 , 147 , 28 , 82 ] [30,147,28,82] [30,147,28,82] Basically, the research is carried out around the solution of this problem , In fact, it is somewhat similar to the above regularization operation , It is nothing more than to align features or output results , The specific operation is as follows Figure 21 Shown .
There are structural dependencies between each sample tag (there are structural dependencies between labels of each sample):
stay Semantic division (semantic segment, This is a concept in computer vision ) And word segmentation ( Such as named entity recognition , Part of speech tagging ) And other low-level classification problems , Feature based adaptation is often not a good choice ( That is, directly embedding words as adaptation ), The reason is that the characteristics of each pixel or word segmentation are high-dimensional , And a sample will contain a lot of pixels or word segmentation . However , There are two sides to everything , In advanced classification problems , The output space of these low-level classification tasks usually contains rich information about distribution ( Such as scene layout information or context information ), Therefore, it is a good choice to adapt directly based on the output space .
Relevant research includes references [ 173 , 182 ] [173,182] [173,182],Figure 21 The lower right figure in corresponds to references [ 173 ] [173] [173]
3.2.3 Hypothetical oppositional learning Hypothesis Adversarial Learning
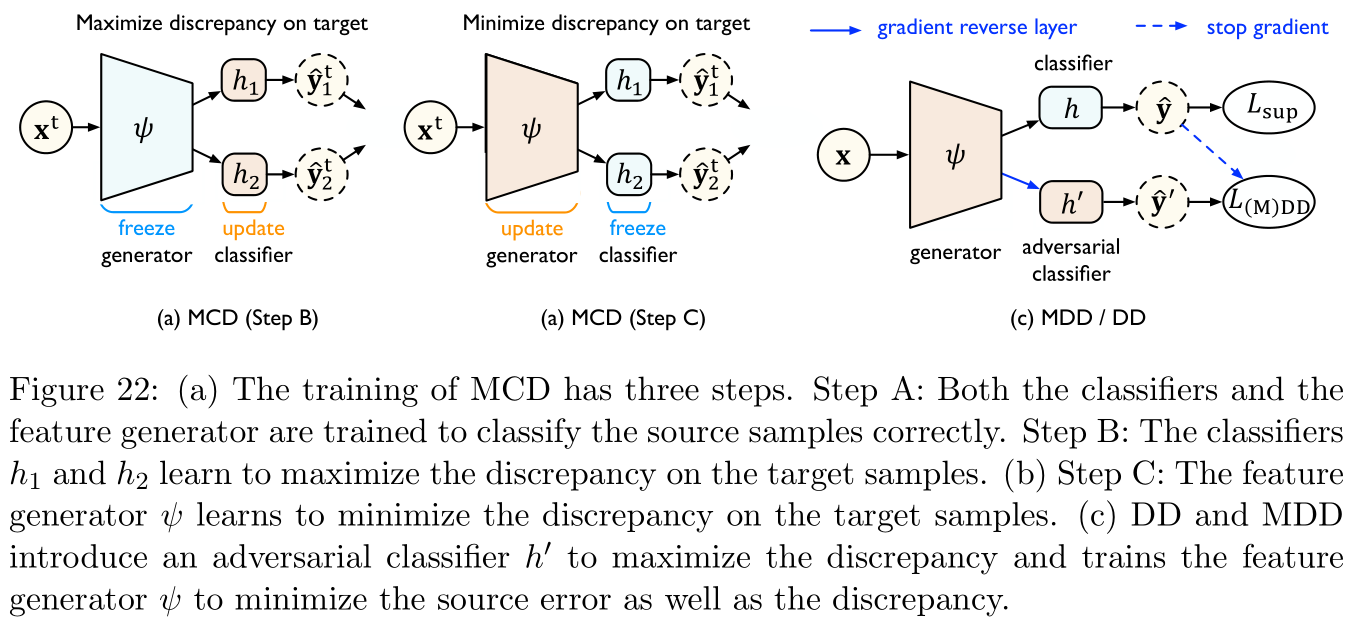
reference [ 146 ] [146] [146] Put forward Maximum classifier gap (maximum classifier discrepancy,MCD) For fully parameterized estimation and optimization H Δ H \mathcal{H\Delta H} HΔH The divergence , Specific as Figure 22 Shown :
- MCD Maximize the gap between the output of two classifiers , And detect target samples that are far from the source distribution ( namely H Δ H \mathcal{H\Delta H} HΔH The divergence ).
- Next, a feature generator is used to learn and generate target features to minimize the domain gap .
- MCD It uses L 1 L_1 L1 Distance to measure the gap .
- Theoretically MCD Than H Δ H \mathcal{H\Delta H} HΔH Divergence can get closer results , However, experiments show that its convergence speed is slow and it is very sensitive to hyperparameters . The possible reasons are MCD Two arbitrary classifiers are used in h h h and h ′ h' h′ To maximize the gap , bring Minimize and maximize (minimax) It is relatively difficult to reach equilibrium .
reference [ 204 ] [204] [204] Proposed The gap is contradictory (disparity discrepancy,DD, It seems to have been mentioned above ) Provides a tighter upper bound , The method is through the assumption space H \mathcal H H Take supremum ( Instead of H Δ H \mathcal H\Delta \mathcal H HΔH), This significantly makes Minimize and maximize Simple . Such as Figure 22 Shown ,DD An opposite classifier is introduced h ′ h' h′( And h h h Belong to the same hypothetical space ), be d h , H ( S , T ) d_{h,\mathcal H}(\mathcal{S,T}) dh,H(S,T) The supremum of is approximately :
L D D ( h , ψ ) = max h ′ E x s ∼ S ^ L s [ h ′ ( ψ ( x s ) ) , h ( ψ ( x s ) ) ] − E x t ∼ T ^ L s [ h ′ ( ψ ( x s ) ) , h ( ψ ( x s ) ) ] (32) L_{\rm DD}(h,\psi)=\max_{h'}\mathbb{E}_{ {\bf x}^s\sim\mathcal{\hat S}}L^s[h'(\psi({\bf x}^s)),h(\psi({\bf x}^s))]-\mathbb{E}_{ {\bf x}^t\sim\mathcal{\hat T}}L^s[h'(\psi({\bf x}^s)),h(\psi({\bf x}^s))]\tag{32} LDD(h,ψ)=h′maxExs∼S^Ls[h′(ψ(xs)),h(ψ(xs))]−Ext∼T^Ls[h′(ψ(xs)),h(ψ(xs))](32)
among L s L^s Ls And L t L^t Lt Is the loss function defined in the source domain and the target domain .Theoretically, the opposite classifier h ′ h' h′ Closer to the supremum , Minimizing the following formula can reduce the target error ϵ T \epsilon_{\mathcal T} ϵT:
min ψ , h E x s , y s ∼ S ^ L C E ( h ( ψ ( x s ) ) , y s ) + λ L D D ( h , ψ ) (33) \min_{\psi,h}\mathbb{E}_{ {\bf x}^s,{\bf y}^s\sim\mathcal{\hat S}}L_{\rm CE}(h(\psi({\bf x}^s)),{\bf y}^s)+\lambda L_{\rm DD}(h,\psi)\tag{33} ψ,hminExs,ys∼S^LCE(h(ψ(xs)),ys)+λLDD(h,ψ)(33)
among λ \lambda λ Is the coefficient of weighing two terms . The intuitive explanation is ,DD Looking for an opposing classifier h ′ h' h′ To correctly predict the samples in the source field , And be able to get in the target field with h h h Different predictions , Then the feature generator ψ \psi ψ It is trained to generate features on this decision boundary to avoid such a situation .DD It can only be used to deal with binary classification problems , So references [ 204 ] [204] [204] It is further extended to Marginal gap contradiction (margin disparity discrepancy,MDD) To deal with the problem of polyphenols :
L M D D ( h , ψ ) = max h ′ γ E x s ∼ S ^ log [ σ h ( ψ ( x s ) ) ( h ′ ( ψ ( x s ) ) ) ] + E x t ∼ T ^ log [ 1 − σ h ( ψ ( x t ) ) ( h ′ ( ψ ( x t ) ) ) ] (34) L_{\rm MDD}(h,\psi)=\max_{h'}\gamma\mathbb{E}_{ {\bf x}^s\sim\mathcal{\hat S}}\log[\sigma_{h(\psi({\bf x}^s))}(h'(\psi({\bf x}^s)))]+\mathbb{E}_{ {\bf x}^t\sim\mathcal{\hat T}}\log[1-\sigma_{h(\psi({\bf x}^t))}(h'(\psi({\bf x}^t)))]\tag{34} LMDD(h,ψ)=h′maxγExs∼S^log[σh(ψ(xs))(h′(ψ(xs)))]+Ext∼T^log[1−σh(ψ(xt))(h′(ψ(xt)))](34)
among γ = exp ρ \gamma=\exp\rho γ=expρ, ρ \rho ρ Is the marginal rate , σ \sigma σ Is the activation function ( Such as softmax), γ \gamma γ The choice of is very critical , It can effectively avoid overestimating the boundary .
3.2.4 Domain translation Domain Translation
Domain translation (domain translation) Refers to the original data ( Text 、 Images 、 Audio etc. ) From the source field S \mathcal S S Map to the target domain T \mathcal T T A kind of task in . In domain adaptability , We can use the translation model ( Usually based on GAN) Obtain tags similar to the source domain samples in the target domain .
in the light of GAN, There are many different variants of improvements , Such as references [ 106 ] [106] [106] Proposed Pairwise confrontation generates Networks (coupled generative adversarial networks,CoGAN) Learn the joint distribution of multi domain image data , That is, multiple different generators need to generate pairs 、 In different fields 、 Tag shared data .CoGAN Joint distribution can be learned without corresponding images in different fields , These generated target samples of shared tags will be used to train models in the target domain .
The objective function of domain translation is usually to learn a mapping G : S → T G:\mathcal{S}\rightarrow\mathcal{T} G:S→T Make the sample generated G ( x ) G({\bf x}) G(x) It is indistinguishable from the training samples in the target field . Such as Figure 23 Shown , reference [ 16 ] [16] [16] Put forward PixelDA Introduce an opposition identifier D D D To distinguish the translated samples from the target samples :
L G A N ( G ) = max D E x ∼ S ^ log [ 1 − D ( G ( x ) ) ] + E x ∼ T ^ log [ D ( x ) ] (35) L_{\rm GAN}(G)=\max_D\mathbb{E}_{ {\bf x}\sim\mathcal{\hat S}}\log[1-D(G({\bf x}))]+\mathbb{E}_{ {\bf x}\sim\mathcal{\hat T}}\log[D({\bf x})]\tag{35} LGAN(G)=DmaxEx∼S^log[1−D(G(x))]+Ex∼T^log[D(x)](35)
generator G G G Try to hope to make G ( x ) G({\bf x}) G(x) As similar as possible to the samples in the target field , So next we need min G L G A N ( G ) \min_G L_{\rm GAN}(G) minGLGAN(G).
Finally, the classifier of each task f f f And feature mining ψ \psi ψ Through supervised training ( In generating data ) adopt :
min ψ , h E ( x , y ) ∼ S ^ L sup ( h ∘ ψ ( G ( x ) ) , y ) \min_{\psi,h}\mathbb{E}_{({\bf x},{\bf y})\sim\mathcal{\hat S}}L_{\sup}(h\circ\psi(G({\bf x})),{\bf y}) ψ,hminE(x,y)∼S^Lsup(h∘ψ(G(x)),y)Periodic consistency (cycle consistency):
GAN It can be used to learn the mapping between data sets in different fields , Here are two questions :
- The sample of the source domain may be mapped to a sample independent of the target domain .
- Samples from multiple different domains may be mapped to samples from the same target domain , This leads to classic Mode collapse (mode collapse, reference [ 54 ] [54] [54]) problem .
From this reference [ 209 ] [209] [209] Put forward CycleGAN, A reverse mapping is introduced F : T → S F:\mathcal{T\rightarrow S} F:T→S( Map from the target domain to the source domain ), Build another Periodic consistency To reduce the possible mapping function space ( Such as Figure 23 Shown ). Specifically, from the perspective of mathematical expression , Periodic consistency need F F F and G G G The two mappings are Double shot (bijections) And they are inverse mappings to each other , In practice F ( G ( x ) ) ≈ x , G ( F ( x ) ) ≈ x F(G({\bf x}))\approx{\bf x},G(F({\bf x}))\approx{\bf x} F(G(x))≈x,G(F(x))≈x, This idea has been widely used in domain adaptability , Such as references [ 72 , 189 , 17 , 85 , 92 , 33 ] [72,189,17,85,92,33] [72,189,17,85,92,33], The last two articles are about natural language processing , It's all about cross language machine translation tasks , The first four articles are all about image processing , Including image classification 、 Semantic division 、 Identity recognition 、 Robot grabs (robotic grasping), Entity recognition, etc .
Semantic consistency (semantic consistency):
It is easy to happen when mapping labels from the source domain to the target domain Label flip (label flipping) problem , This leads to Semantic consistency It refers to the hope to make the sample x \bf x x Consistent with the translated samples , namely f ( x ) = f ( G ( x ) ) f({\bf x})=f(G({\bf x})) f(x)=f(G(x)). because f f f Unknown , So references [ 169 , 72 , 17 ] [169,72,17] [169,72,17] Put forward a series of Proxy functions (proxy function), That is, in a given proxy function h p h_{\rm p} hp And distance measurement d d d Under the circumstances , The objective function is to reduce semantic inconsistencies :
min G L S C ( G , h p ) = d ( h p ( x ) , h p ( G ( x ) ) ) (36) \min_GL_{\rm SC}(G,h_{\rm p})=d(h_{\rm p}({\bf x}),h_{\rm p}(G({\bf x})))\tag{36} GminLSC(G,hp)=d(hp(x),hp(G(x)))(36)If the difference in the field is mainly low ( Text 、 describe 、 Color, etc. ), Translation methods can effectively make up for domain differences , But if it is advanced ( Such as Camera angle ,camera angles), Translation methods usually don't work .
3.2.5 Semi-supervised learning Semi-Supervised Learning
Unsupervised domain adaptability (UDA) And Semi-supervised learning (SSL) Is closely related to the , many SSL Methods can be applied to UDA in .
Semi-supervised learning Three assumptions :
- Smoothness assumption (smoothness assumption): If two samples x 1 , x 2 {\bf x}_1,{\bf x}_2 x1,x2 In high-density areas, the distance is similar , Then their output y 1 , y 2 {\bf y}_1,{\bf y_2} y1,y2 It should also be similar .
- Cluster hypothesis (cluster assumption): If the sample points are in the same cluster , Then they are probably of the same type .
- manifold hypothesis ( assumption): High dimensional data can be approximated to a low dimension manifold( This word seems to be untranslatable ) in .
Can be used for UDA Some of SSL Method :
Uniform regularization (consistency regularization): It means that similar sample points should get consistent prediction results , Relevant research includes references [ 44 , 48 ] [44,48] [44,48].
Entropy minimization (entropy minimization): Make the model have the highest confidence for the unlabeled data ( That is, the lowest entropy ) Predicted results , It is often used as an auxiliary method of adaptive methods in many fields , Relevant research includes references [ 82.104 ] [82.104] [82.104].
False labeling (pseudo-labeling): Generate proxy labels for unmarked data , And use these noisy tags to mix with the labeled data for training . Relevant research includes references [ 212 , 201 , 205 ] [212,201,205] [212,201,205], It is particularly mentioned here that the cross entropy loss is highly sensitive to noise labels , So references [ 143 , 105 ] [143,105] [143,105] It is proposed that Generalized cross entropy loss (generalized cross-entropy,GCE) As a solution :
L G C E ( x , y ~ ) = 1 q ( 1 − h y ~ ( x ) q ) (37) L_{\rm GCE}({\bf x},\tilde y)=\frac1q(1-h_{\tilde y}({\bf x})^q)\tag{37} LGCE(x,y~)=q1(1−hy~(x)q)(37)
among q ∈ ( 0 , 1 ] q\in(0,1] q∈(0,1] It is a super parameter used to weigh the two loss functions of cross entropy and mean absolute value error .
3.2.6 notes Remarks
Summarize the performance of all methods in this section :
| Method | Adaptability | Data efficiency | Modal ductility | Task extensibility | Theoretical guarantee |
|---|---|---|---|---|---|
| Statistical matching | Bad | optimal | optimal | in | optimal |
| Domain opposite learning | in | in | optimal | in | optimal |
| Hypothetical oppositional learning | optimal | in | optimal | in | optimal |
| Domain translation | in | Bad | Bad | optimal | Bad |
| Semi-supervised learning | in | in | in | Bad | Bad |
Field description :
- Adaptability (adaptation performance): Model performance when there is a large amount of annotation data in downstream tasks .
- Data efficiency (data efficiency): Model performance when there is only a small amount of data in downstream tasks .
- Modal ductility (modality scalability): Can it be used for multimodal data , Text 、 picture 、 Audio-visual .
- Task extensibility (task scalability): Can you easily migrate the pre training model to different downstream tasks .
- Theoretical guarantee (theory guarantee): Whether the generalization error of the target field in adaptation can be controlled within a certain limit .
4 assessment Evaluation
4.1 Data sets Datasets
General language comprehension assessment (general language understanding evaluation,GLUE, reference [ 183 ] [183] [183]) It is the most famous benchmark in the field of natural language processing , The following table illustrates a series of GLUE Data set of , Language comprehension tasks including nine sentences or sentence pairs :
| Corpus | The amount of training data | Test data volume | Evaluation indicators | Task type | field |
|---|---|---|---|---|---|
| CoLA \text{CoLA} CoLA | 8.5 k 8.5\rm k 8.5k | 1 k 1\rm k 1k | Matthews correlation coefficient | Acceptability | blend |
| SST-2 \text{SST-2} SST-2 | 67 k 67\rm k 67k | 1.8 k 1.8\rm k 1.8k | accuracy | Sentiment analysis | Film review |
| MRPC \text{MRPC} MRPC | 3.7 k 3.7\rm k 3.7k | 1.7 k 1.7\rm k 1.7k | accuracy / F1-score \text{F1-score} F1-score | The phrase | Journalism |
| STS-B \text{STS-B} STS-B | 7 k 7\rm k 7k | 1.4 k 1.4\rm k 1.4k | Pearson correlation coefficient | Sentence similarity | blend |
| QQP \text{QQP} QQP | 364 k 364\rm k 364k | 391 k 391\rm k 391k | accuracy / F1-score \text{F1-score} F1-score | The phrase | Social Q & A |
| MNLI \text{MNLI} MNLI | 393 k 393\rm k 393k | 20 k 20\rm k 20k | ( Not ) Matching accuracy | Natural language inference | blend |
| QNLI \text{QNLI} QNLI | 105 k 105\rm k 105k | 5.4 k 5.4\rm k 5.4k | accuracy | Question and answer / Natural language inference | Wikipedia |
| RTE \text{RTE} RTE | 2.5 k 2.5\rm k 2.5k | 3 k 3\rm k 3k | accuracy | Natural language inference | News and Wikipedia |
| WNLI \text{WNLI} WNLI | 634 634 634 | 146 146 146 | accuracy | Co refer to / Natural language inference | Science fiction books |
- The authors note : The last data set may have a small amount of data .
But there is still no similar GLUE Benchmark for computer vision , Here are just some commonly used data sets in the field of image processing :
| Data sets | The amount of training data | Test data volume | Number of categories | Evaluation indicators | field |
|---|---|---|---|---|---|
| Food-101 \text{Food-101} Food-101( reference [ 88 ] [88] [88]) | 75750 75750 75750 | 25250 25250 25250 | 101 101 101 | top-1 \text{top-1} top-1 | blend |
| CIFAR-10 \text{CIFAR-10} CIFAR-10( reference [ 88 ] [88] [88]) | 50000 50000 50000 | 10000 10000 10000 | 10 10 10 | top-1 \text{top-1} top-1 | blend |
| cIFAR-100 \text{cIFAR-100} cIFAR-100( reference [ 88 ] [88] [88]) | 50000 50000 50000 | 10000 10000 10000 | 100 100 100 | top-1 \text{top-1} top-1 | blend |
| SUN397 \text{SUN397} SUN397( reference [ 88 ] [88] [88]) | 19850 19850 19850 | 19850 19850 19850 | 397 397 397 | top-1 \text{top-1} top-1 | blend |
| Stanford Cars \text{Stanford Cars} Stanford Cars( reference [ 88 ] [88] [88]) | 8144 8144 8144 | 8041 8041 8041 | 196 196 196 | top-1 \text{top-1} top-1 | blend |
| FGVC Aircraft \text{FGVC Aircraft} FGVC Aircraft( reference [ 88 ] [88] [88]) | 6667 6667 6667 | 3333 3333 3333 | 100 100 100 | mean per-class \text{mean per-class} mean per-class | blend |
| Describable Textures(DTD) \text{Describable Textures(DTD)} Describable Textures(DTD)( reference [ 88 ] [88] [88]) | 3760 3760 3760 | 1880 1880 1880 | 47 47 47 | top-1 \text{top-1} top-1 | blend |
| Oxford-III Pets \text{Oxford-III Pets} Oxford-III Pets( reference [ 88 ] [88] [88]) | 3680 3680 3680 | 3369 3369 3369 | 37 37 37 | mean per-class \text{mean per-class} mean per-class | blend |
| Caltech-101 \text{Caltech-101} Caltech-101( reference [ 88 ] [88] [88]) | 3060 3060 3060 | 6084 6084 6084 | 102 102 102 | mean per-class \text{mean per-class} mean per-class | blend |
| Oxford 102 flowers \text{Oxford 102 flowers} Oxford 102 flowers | 2040 2040 2040 | 6149 6149 6149 | 102 102 102 | top-1 \text{top-1} top-1 | blend |
| ImageNet-R \text{ImageNet-R} ImageNet-R( reference [ 69 ] [69] [69]) | − - − | 30 k 30\rm k 30k | 200 200 200 | top-1 \text{top-1} top-1 | blend |
| ImageNet-Sketch \text{ImageNet-Sketch} ImageNet-Sketch( reference [ 84 ] [84] [84]) | − - − | 50 k 50\rm k 50k | 1000 1000 1000 | top-1 \text{top-1} top-1 | draft |
| DomainNet-c \text{DomainNet-c} DomainNet-c( reference [ 128 ] [128] [128]) | 33525 33525 33525 | 14604 14604 14604 | 365 365 365 | top-1 \text{top-1} top-1 | Clip art |
| DomainNet-p \text{DomainNet-p} DomainNet-p( reference [ 128 ] [128] [128]) | 50416 50416 50416 | 21850 21850 21850 | 365 365 365 | top-1 \text{top-1} top-1 | Oil Painting |
| DomainNet-r \text{DomainNet-r} DomainNet-r( reference [ 128 ] [128] [128]) | 120906 120906 120906 | 52041 52041 52041 | 365 365 365 | top-1 \text{top-1} top-1 | blend |
| DomainNet-s \text{DomainNet-s} DomainNet-s( reference [ 128 ] [128] [128]) | 48212 48212 48212 | 20916 20916 20916 | 365 365 365 | top-1 \text{top-1} top-1 | draft |
4.2 Open source package Library
Project address :[email protected]( Have in hand )
Usage method : Official documents @TLlib
Here's a simple one DANN Application code example :
# define the domain discriminator from dalib.modules.domain_discriminator import DomainDiscriminator discriminator = DomainDiscriminator(in_feature=1024, hidden_size=1024) # define the domain adversarial loss module from dalib.adptation.dann import DomainAdversarialLoss dann = DomainAdversarialLoss(discriminator, reduction='mean') # features from the source and target domain f_s, f_t = torch.randn(20, 1024), torch.randn(20, 1024) # calculate the final loss loss = dann(f_s, f_t)at present TLlib mainly PyTorch Implementation as a backend , It has good ductility .
4.3 The benchmark Benchmark
This section is mainly about Section 4.1 The benchmark of typical methods of pre training and adaptation on several large-scale data sets mentioned in , Some of the benchmark results are through TLlib Realize the .
4.3.1 Preliminary training Pre-Training
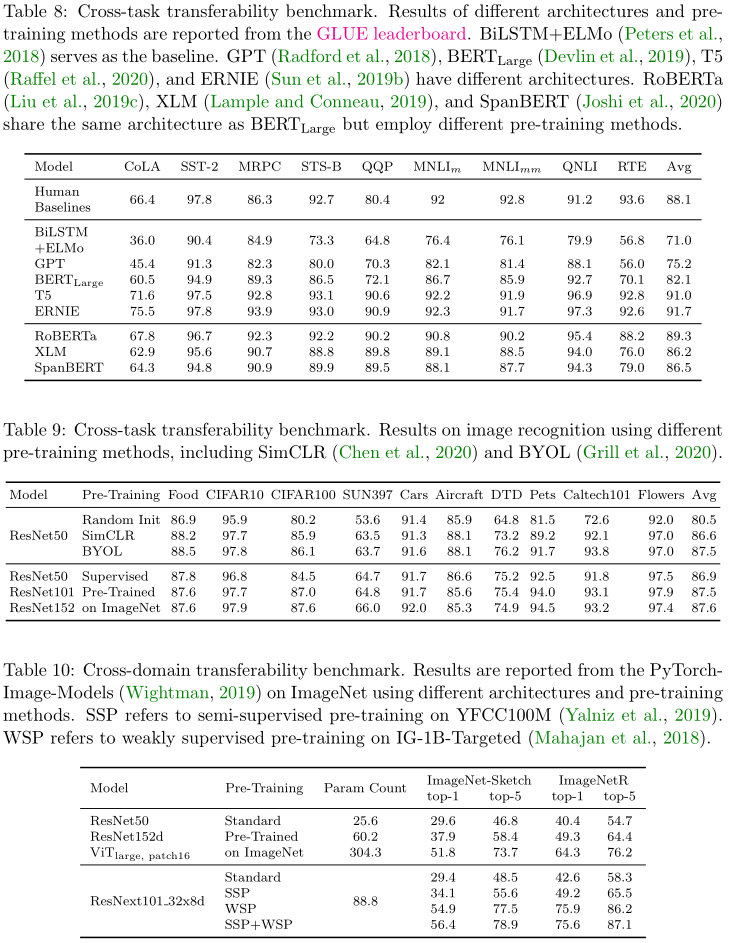
4.3.2 Task adaptability Task Adaptation
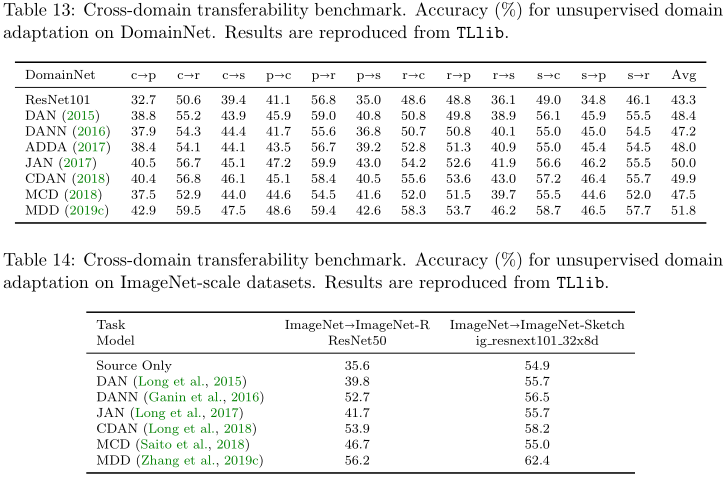
4.3.3 Domain adaptability Domain Adaptation
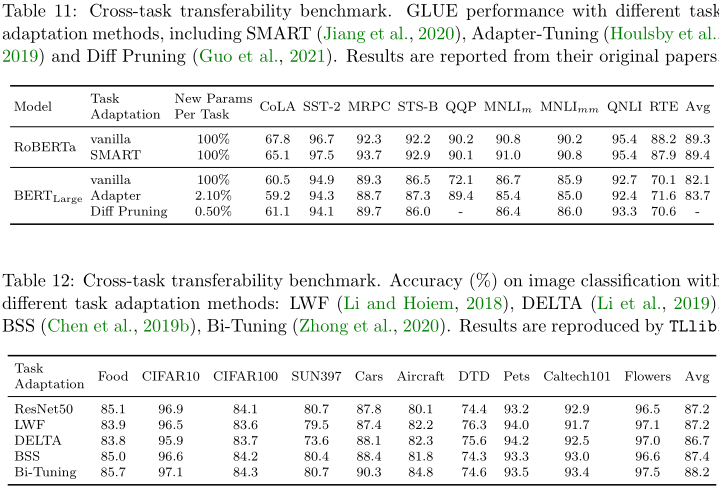
5 Conclusion Conclusion
In this paper, we investigate how to acquire and apply transferability in the whole lifecycle of deep learning. In the pre-training section, we focus on how to improve the transferability of the pre-trained models by designing architecture, pre-training task, and training strategy. In the task adaptation section, we discuss how to better preserve and utilize the transferable knowledge to improve the performance of target tasks. In the domain adaptation section, we illustrate how to bridge the domain gap to increase the transferability for real applications. This survey connects many isolated areas with their relation to transferability and provides a unified perspective to explore transferability in deep learning. We expect this study will attract the community’s attention to the fundamental role of transferability in deep learning.
reference
[001] Samira Abnar, Mostafa Dehghani, Behnam Neyshabur, and Hanie Sedghi. Exploring the limits of large scale pre-training. In ICLR, 2022.
[002] Armen Aghajanyan, Luke Zettlemoyer, and Sonal Gupta. Intrinsic dimensionality explains the effectiveness of language model fine-tuning. In ACL, 2021.
[003] Dario Amodei, Sundaram Ananthanarayanan, Rishita Anubhai, Jingliang Bai, Eric Battenberg, Carl Case, Jared Casper, Bryan Catanzaro, Qiang Cheng, Guoliang Chen, et al. Deep speech 2: End-to-end speech recognition in english and mandarin. In ICML, 2016.
[004] Martin Arjovsky, L´eon Bottou, Ishaan Gulrajani, and David Lopez-Paz. Invariant risk minimization. arXiv preprint arXiv:1907.02893, 2019.
[005] Sanjeev Arora, Rong Ge, Yingyu Liang, Tengyu Ma, and Yi Zhang. Generalization and equilibrium in generative adversarial nets (GANs). In ICML, 2017.
[006] Peter L. Bartlett and Shahar Mendelson. Rademacher and gaussian complexities: Risk bounds and structural results. In JMLR, 2002.
[007] Iz Beltagy, Kyle Lo, and Arman Cohan. Scibert: Pretrained language model for scientific text. In EMNLP, 2019.
[008] S. Ben-David, J. Blitzer, K. Crammer, A. Kulesza, F. Pereira, and J. W. Vaughan. A theory of learning from different domains. Machine Learning, 79, page 151–175, 2010a.
[009] Shai Ben-David, John Blitzer, Koby Crammer, and Fernando Pereira. Analysis of representations for domain adaptation. In NeurIPS, 2006.
[010] Shai Ben-David, Tyler Lu, Teresa Luu, and David Pal. Impossibility theorems for domain adaptation. In AISTATS, pages 129–136, 2010b.
[011] Yoshua Bengio. Deep learning of representations for unsupervised and transfer learning. In ICML workshop, 2012.
[012] Yoshua Bengio, Pascal Lamblin, Dan Popovici, and Hugo Larochelle. Greedy layer-wise training of deep networks. In NeurIPS, 2007.
[013] Yoshua Bengio, Aaron Courville, and Pascal Vincent. Representation learning: A review and new perspectives. TPAMI, 35(8):1798–1828, 2013.
[014] Yoshua Bengio, Yann Lecun, and Geoffrey Hinton. Deep learning for ai. Communications of the ACM, 64(7):58–65, 2021.
[015] Konstantinos Bousmalis, George Trigeorgis, Nathan Silberman, Dilip Krishnan, and Dumitru Erhan. Domain separation networks. In NeurIPS, 2016.
[016] Konstantinos Bousmalis, Nathan Silberman, David Dohan, Dumitru Erhan, and Dilip Krishnan. Unsupervised pixel-level domain adaptation with generative adversarial networks. In CVPR, 2017.
[017] Konstantinos Bousmalis, Alex Irpan, Paul Wohlhart, Yunfei Bai, Matthew Kelcey, Mrinal Kalakrishnan, Laura Downs, Julian Ibarz, Peter Pastor, Kurt Konolige, Sergey Levine, and Vincent Vanhoucke. Using simulation and domain adaptation to improve efficiency of deep robotic grasping. In ICRA, 2018.
[018] Tom B Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, et al. Language models are few-shot learners. In NeurIPS, 2020.
[019] Pau Panareda Busto and Juergen Gall. Open set domain adaptation. In ICCV, 2017.
[020] Rich Caruana. Multitask learning. Technical report, 1997.
[021] Olivier Chapelle, Bernhard Sch¨olkopf, and Alexander Zien. Semi-Supervised Learning (Adaptive Computation and Machine Learning). The MIT Press, 2006. ISBN 0262033585.
[022] Minmin Chen, Zhixiang Xu, Kilian Q. Weinberger, and Fei Sha. Marginalized denoising autoencoders for domain adaptation. In ICML, 2012.
[023] Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. A simple framework for contrastive learning of visual representations. In ICML, 2020.
[024] Wei-Yu Chen, Yen-Cheng Liu, Zsolt Kira, Yu-Chiang Frank Wang, and Jia-Bin Huang. A closer look at few-shot classification. In ICLR, 2019a.
[025] Xinlei Chen and Kaiming He. Exploring simple siamese representation learning. In CVPR, 2021.
[026] Xinlei Chen, Saining Xie, and Kaiming He. An empirical study of training self-supervised vision transformers. arXiv preprint arXiv:2104.02057, 2021a.
[027] Xinyang Chen, Sinan Wang, Bo Fu, Mingsheng Long, and Jianmin Wang. Catastrophic forgetting meets negative transfer: Batch spectral shrinkage for safe transfer learning. In NeurIPS, 2019b.
[028] Xinyang Chen, Sinan Wang, Mingsheng Long, and Jianmin Wang. Transferability vs. discriminability: Batch spectral penalization for adversarial domain adaptation. In ICML, 2019c.
[029] Xinyang Chen, Sinan Wang, Jianmin Wang, and Mingsheng Long. Representation subspace distance for domain adaptation regression. In ICML, 2021b.
[030] Yuhua Chen, Wen Li, Christos Sakaridis, Dengxin Dai, and Luc Van Gool. Domain adaptive faster R-CNN for object detection in the wild. In CVPR, 2018.
[031] Kyunghyun Cho, Bart van Merri¨enboer, Caglar Gulcehre, Dzmitry Bahdanau, Fethi Bougares, Holger Schwenk, and Yoshua Bengio. Learning phrase representations using RNN encoder–decoder for statistical machine translation. In EMNLP, 2014.
[032] Alexandra Chronopoulou, Christos Baziotis, and Alexandros Potamianos. An embarrassingly simple approach for transfer learning from pretrained language models. In NAACL, 2019.
[033] Alexis Conneau, Guillaume Lample, Ruty Rinott, Adina Williams, Samuel R. Bowman, Holger Schwenk, and Veselin Stoyanov. XNLI: evaluating cross-lingual sentence representations. In EMNLP, 2018.
[034] Nicolas Courty, R´emi Flamary, Amaury Habrard, and Alain Rakotomamonjy. Joint distribution optimal transportation for domain adaptation. In NeurIPS, 2017.
[035] Yin Cui, Yang Song, Chen Sun, Andrew Howard, and Serge Belongie. Large scale finegrained categorization and domain-specific transfer learning. In CVPR, pages 4109–4118, 2018.
[036] Bharath Bhushan Damodaran, Benjamin Kellenberger, R´emi Flamary, Devis Tuia, and Nicolas Courty. Deepjdot: Deep joint distribution optimal transport for unsupervised domain adaptation. In ECCV, 2018.
[037] Matthias Delange, Rahaf Aljundi, Marc Masana, Sarah Parisot, Xu Jia, Ales Leonardis, Greg Slabaugh, and Tinne Tuytelaars. A continual learning survey: Defying forgetting in classification tasks. TPAMI, page 1–20, 2021.
[038] Jia Deng, Wei Dong, Richard Socher, Li-Jia Li, Kai Li, and Li Fei-Fei. Imagenet: A largescale hierarchical image database. In CVPR, 2009.
[039] Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. Bert: Pre-training of deep bidirectional transformers for language understanding. In NAACL, 2019.
[040] Carl Doersch, Abhinav Gupta, and Alexei A. Efros. Unsupervised visual representation learning by context prediction. In ICCV, 2015.
[041] Jeff Donahue, Yangqing Jia, Oriol Vinyals, Judy Hoffman, Ning Zhang, Eric Tzeng, and Trevor Darrell. Decaf: A deep convolutional activation feature for generic visual recognition. In ICML, 2014.
[042] Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, Xiaohua Zhai, Thomas Unterthiner, Mostafa Dehghani, Matthias Minderer, Georg Heigold, Sylvain Gelly, Jakob Uszkoreit, and Neil Houlsby. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. In ICLR, 2021.
[043] Chelsea Finn, Pieter Abbeel, and Sergey Levine. Model-agnostic meta-learning for fast adaptation of deep networks. In ICML, 2017.
[044] Geoffrey French, Michal Mackiewicz, and Mark H. Fisher. Self-ensembling for domain adaptation. In ICLR, 2018.
[045] Yaroslav Ganin and Victor Lempitsky. Unsupervised domain adaptation by backpropagation. In ICML, 2015.
[046] Yaroslav Ganin, Evgeniya Ustinova, Hana Ajakan, Pascal Germain, Hugo Larochelle, Fran¸cois Laviolette, Mario March, and Victor Lempitsky. Domain-adversarial training of neural networks. JMLR, 17(59):1–35, 2016.
[047] Victor Garcia and Joan Bruna. Few-shot learning with graph neural networks. In ICLR, 2018.
[048] Yixiao Ge, Dapeng Chen, and Hongsheng Li. Mutual mean-teaching: Pseudo label refinery for unsupervised domain adaptation on person re-identification. In ICLR, 2020.
[049] Robert Geirhos, Patricia Rubisch, Claudio Michaelis, Matthias Bethge, Felix A Wichmann, and Wieland Brendel. Imagenet-trained cnns are biased towards texture; increasing shape bias improves accuracy and robustness. In ICLR, 2019.
[050] Ross Girshick, Jeff Donahue, Trevor Darrell, and Jitendra Malik. Rich feature hierarchies for accurate object detection and semantic segmentation. In CVPR, 2014.
[051] Xavier Glorot, Antoine Bordes, and Yoshua Bengio. Domain adaptation for large-scale sentiment classification: A deep learning approach. In ICML, 2011.
[052] Boqing Gong, Yuan Shi, Fei Sha, and Kristen Grauman. Geodesic flow kernel for unsupervised domain adaptation. In CVPR, 2012.
[053] Boqing Gong, Kristen Grauman, and Fei Sha. Connecting the dots with landmarks: Discriminatively learning domain-invariant features for unsupervised domain adaptation. In ICML, 2013.
[054] Ian J Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative adversarial networks. In NeurIPS, 2014.
[055] Ian J Goodfellow, Jonathon Shlens, and Christian Szegedy. Explaining and harnessing adversarial examples. 2015.
[056] Anirudh Goyal, Alex Lamb, Jordan Hoffmann, Shagun Sodhani, Sergey Levine, Yoshua Bengio, and Bernhard Sch¨olkopf. Recurrent independent mechanisms. In ICLR, 2021.
[057] Arthur Gretton, Karsten M. Borgwardt, Malte J. Rasch, Bernhard Sch¨olkopf, and Alexander Smola. A kernel two-sample test. JMLR, 13(25):723–773, 2012a.
[058] Arthur Gretton, Dino Sejdinovic, Heiko Strathmann, Sivaraman Balakrishnan, Massimiliano Pontil, Kenji Fukumizu, and Bharath K Sriperumbudur. Optimal kernel choice for large-scale two-sample tests. In NeurIPS, 2012b.
[059] Jean-Bastien Grill, Florian Strub, Florent Altch´e, Corentin Tallec, Pierre Richemond, Elena Buchatskaya, Carl Doersch, Bernardo Avila Pires, Zhaohan Guo, Mohammad Gheshlaghi Azar, Bilal Piot, koray kavukcuoglu, Remi Munos, and Michal Valko. Bootstrap your own latent - a new approach to self-supervised learning. In NeurIPS, 2020.
[060] Ishaan Gulrajani and David Lopez-Paz. In search of lost domain generalization. In ICLR, 2021.
[061] Demi Guo, Alexander Rush, and Yoon Kim. Parameter-efficient transfer learning with diff pruning. In ACL, 2021.
[062] Yunhui Guo, Honghui Shi, Abhishek Kumar, Kristen Grauman, Tajana Rosing, and Rogerio Feris. Spottune: transfer learning through adaptive fine-tuning. In CVPR, 2019.
[063] Suchin Gururangan, Ana Marasovi´c, Swabha Swayamdipta, Kyle Lo, Iz Beltagy, Doug Downey, and Noah A. Smith. Don’t stop pretraining: Adapt language models to domains and tasks. In ACL, 2020.
[064] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In CVPR, 2016.
[065] Kaiming He, Georgia Gkioxari, Piotr Doll´ar, and Ross Girshick. Mask r-cnn. In ICCV, 2017.
[066] Kaiming He, Ross Girshick, and Piotr Doll´ar. Rethinking imagenet pre-training. In ICCV, 2019.
[067] Kaiming He, Haoqi Fan, Yuxin Wu, Saining Xie, and Ross Girshick. Momentum contrast for unsupervised visual representation learning. In CVPR, 2020.
[068] Kaiming He, Xinlei Chen, Saining Xie, Yanghao Li, Piotr Doll´ar, and Ross Girshick. Masked autoencoders are scalable vision learners. arXiv preprint arXiv:2111.06377, 2021.
[069] Dan Hendrycks, Steven Basart, Norman Mu, Saurav Kadavath, Frank Wang, Evan Dorundo, Rahul Desai, Tyler Zhu, Samyak Parajuli, Mike Guo, Dawn Song, Jacob Steinhardt, and Justin Gilmer. The many faces of robustness: A critical analysis of out-ofdistribution generalization. ICCV, 2021.
[070] R Devon Hjelm, Alex Fedorov, Samuel Lavoie-Marchildon, Karan Grewal, Phil Bachman, Adam Trischler, and Yoshua Bengio. Learning deep representations by mutual information estimation and maximization. In ICLR, 2019.
[071] Judy Hoffman, Dequan Wang, Fisher Yu, and Trevor Darrell. Fcns in the wild: Pixel-level adversarial and constraint-based adaptation. 2016.
[072] Judy Hoffman, Eric Tzeng, Taesung Park, Jun-Yan Zhu, Phillip Isola, Kate Saenko, Alexei Efros, and Trevor Darrell. Cycada: Cycle-consistent adversarial domain adaptation. In ICML, 2018.
[073] Neil Houlsby, Andrei Giurgiu, Stanislaw Jastrzebski, Bruna Morrone, Quentin De Laroussilhe, Andrea Gesmundo, Mona Attariyan, and Sylvain Gelly. Parameter-efficient transfer learning for NLP. In ICML, 2019.
[074] Jeremy Howard and Sebastian Ruder. Universal language model fine-tuning for text classification. In ACL, 2018.
[075] Weihua Hu, Bowen Liu, Joseph Gomes, Marinka Zitnik, Percy Liang, Vijay S. Pande, and Jure Leskovec. Pre-training graph neural networks. In ICLR, 2020.
[076] Jiayuan Huang, Arthur Gretton, Karsten Borgwardt, Bernhard Sch¨olkopf, and Alex Smola. Correcting sample selection bias by unlabeled data. In NeurIPS, 2007.
[077] Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In ICML, 2015.
[078] Yunhun Jang, Hankook Lee, Sung Ju Hwang, and Jinwoo Shin. Learning what and where to transfer. In ICML, 2019.
[079] Haoming Jiang, Pengcheng He, Weizhu Chen, Xiaodong Liu, Jianfeng Gao, and Tuo Zhao. SMART: robust and efficient fine-tuning for pre-trained natural language models through principled regularized optimization. In ACL, 2020.
[080] Junguang Jiang, Yifei Ji, Ximei Wang, Yufeng Liu, Jianmin Wang, and Mingsheng Long. Regressive domain adaptation for unsupervised keypoint detection. In CVPR, 2021.
[081] Junguang Jiang, Baixu Chen, Jianmin Wang, and Mingsheng Long. Decoupled adaptation for cross-domain object detection. In ICLR, 2022.
[082] Ying Jin, Ximei Wang, Mingsheng Long, and Jianmin Wang. Minimum class confusion for versatile domain adaptation. In ECCV, 2020.
[083] Mandar Joshi, Danqi Chen, Yinhan Liu, Daniel S. Weld, Luke Zettlemoyer, and Omer Levy. SpanBERT: Improving pre-training by representing and predicting spans. In TACL, 2020.
[084] Guoliang Kang, Lu Jiang, Yi Yang, and Alexander G Hauptmann. Contrastive adaptation network for unsupervised domain adaptation. In CVPR, 2019.
[085] Taekyung Kim, Minki Jeong, Seunghyeon Kim, Seokeon Choi, and Changick Kim. Diversify and match: A domain adaptive representation learning paradigm for object detection. In CVPR, 2019.
[086] James Kirkpatrick, Razvan Pascanu, Neil Rabinowitz, Joel Veness, Guillaume Desjardins, Andrei A Rusu, Kieran Milan, John Quan, Tiago Ramalho, Agnieszka GrabskaBarwinska, et al. Overcoming catastrophic forgetting in neural networks. PNAS, 114 (13):3521–3526, 2017.
[087] Alexander Kolesnikov, Lucas Beyer, Xiaohua Zhai, Joan Puigcerver, Jessica Yung, Sylvain Gelly, and Neil Houlsby. Big transfer (bit): General visual representation learning. In ECCV, 2020.
[088] Simon Kornblith, Jonathon Shlens, and Quoc V Le. Do better imagenet models transfer better? In CVPR, 2019.
[089] Zhi Kou, Kaichao You, Mingsheng Long, and Jianmin Wang. Stochastic normalization. In NeurIPS, 2020.
[090] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E. Hinton. Imagenet classification with deep convolutional neural networks. In NeurIPS, 2012.
[091] Guillaume Lample and Alexis Conneau. Cross-lingual language model pretraining. In NeurIPS, 2019.
[092] Guillaume Lample, Ludovic Denoyer, and Marc’Aurelio Ranzato. Unsupervised machine translation using monolingual corpora only. In ICLR, 2017.
[093] Zhenzhong Lan, Mingda Chen, Sebastian Goodman, Kevin Gimpel, Piyush Sharma, and Radu Soricut. Albert: A lite bert for self-supervised learning of language representations. In ICLR, 2020.
[094] Yann LeCun, Yoshua Bengio, and Geoffrey Hinton. Deep learning. Nature, 521(7553): 436–444, 2015.
[095] Chen-Yu Lee, Tanmay Batra, Mohammad Haris Baig, and Daniel Ulbricht. Sliced wasserstein discrepancy for unsupervised domain adaptation. In CVPR, 2019.
[096] Cheolhyoung Lee, Kyunghyun Cho, and Wanmo Kang. Mixout: Effective regularization to finetune large-scale pretrained language models. In ICLR, 2020a.
[097] Jinhyuk Lee, Wonjin Yoon, Sungdong Kim, Donghyeon Kim, Sunkyu Kim, Chan Ho So, and Jaewoo Kang. Biobert: a pre-trained biomedical language representation model for biomedical text mining. Bioinformatics, 36(4):1234–1240, 2020b.
[098] Mike Lewis, Yinhan Liu, Naman Goyal, Marjan Ghazvininejad, Abdelrahman Mohamed, Omer Levy, Veselin Stoyanov, and Luke Zettlemoyer. BART: Denoising Sequence-toSequence Pre-training for Natural Language Generation, Translation, and Comprehension. In ACL, 2020.
[099] Chunyuan Li, Heerad Farkhoor, Rosanne Liu, and Jason Yosinski. Measuring the intrinsic dimension of objective landscapes. In ICLR, 2018.
[100] Xiang Lisa Li and Percy Liang. Prefix-tuning: Optimizing continuous prompts for generation. In ACL, 2021.
[101] Xingjian Li, Haoyi Xiong, Hanchao Wang, Yuxuan Rao, Liping Liu, Zeyu Chen, and Jun Huan. Delta: Deep learning transfer using feature map with attention for convolutional networks. In ICLR, 2019.
[102] Yanghao Li, Naiyan Wang, Jianping Shi, Jiaying Liu, and Xiaodi Hou. Revisiting batch normalization for practical domain adaptation. In ICLR Workshop, 2017.
[103] Zhizhong Li and Derek Hoiem. Learning without forgetting. TPAMI, 40(12):2935–2947, 2018.
[104] Jian Liang, Dapeng Hu, and Jiashi Feng. Do we really need to access the source data? source hypothesis transfer for unsupervised domain adaptation. In ICML, 2020.
[105] Hong Liu, Jianmin Wang, and Mingsheng Long. Cycle self-training for domain adaptation. In NeurIPS, 2021a.
[106] Ming-Yu Liu and Oncel Tuzel. Coupled generative adversarial networks. In NeurIPS, 2016.
[107] Pengfei Liu, Weizhe Yuan, Jinlan Fu, Zhengbao Jiang, Hiroaki Hayashi, and Graham Neubig. Pre-train, prompt, and predict: A systematic survey of prompting methods in natural language processing, 2021b.
[108] Xiaodong Liu, Pengcheng He, Weizhu Chen, and Jianfeng Gao. Multi-task deep neural networks for natural language understanding. In ACL, 2019a.
[109] Yinhan Liu, Myle Ott, Naman Goyal, Jingfei Du, Mandar Joshi, Danqi Chen, Omer Levy, Mike Lewis, Luke Zettlemoyer, and Veselin Stoyanov. Roberta: A robustly optimized bert pretraining approach. arXiv preprint arXiv:1907.11692, 2019b.
[110] Yinhan Liu, Myle Ott, Naman Goyal, Jingfei Du, Mandar Joshi, Danqi Chen, Omer Levy, Mike Lewis, Luke Zettlemoyer, and Veselin Stoyanov. Roberta: A robustly optimized BERT pretraining approach. 2019c.
[111] Mingsheng Long, Jianmin Wang, Guiguang Ding, Jiaguang Sun, and Philip S. Yu. Transfer feature learning with joint distribution adaptation. In ICCV, 2013.
[112] Mingsheng Long, Yue Cao, Jianmin Wang, and Michael I. Jordan. Learning transferable features with deep adaptation networks. In ICML, 2015.
[113] Mingsheng Long, Jianmin Wang, and Michael I. Jordan. Unsupervised domain adaptation with residual transfer networks. In NeurIPS, 2016.
[114] Mingsheng Long, Han Zhu, Jianmin Wang, and Michael I Jordan. Deep transfer learning with joint adaptation networks. In ICML, 2017.
[115] Mingsheng Long, Zhangjie Cao, Jianmin Wang, and Michael I. Jordan. Conditional adversarial domain adaptation. In NeurIPS, 2018.
[116] Mingsheng Long, Yue Cao, Zhangjie Cao, Jianmin Wang, and Michael I. Jordan. Transferable representation learning with deep adaptation networks. TPAMI, 41(12):3071–3085, 2019.
[117] Christos Louizos, Max Welling, and Diederik P. Kingma. Learning sparse neural networks through l 0 regularization. In ICLR, 2018.
[118] Dhruv Mahajan, Ross Girshick, Vignesh Ramanathan, Kaiming He, Manohar Paluri, Yixuan Li, Ashwin Bharambe, and Laurens van der Maaten. Exploring the limits of weakly supervised pretraining. In ECCV, 2018.
[119] Arun Mallya and Svetlana Lazebnik. Piggyback: Adding multiple tasks to a single, fixed network by learning to mask. In ECCV, 2018.
[120] Yishay Mansour, Mehryar Mohri, and Afshin Rostamizadeh. Domain adaptation: Learning bounds and algorithms. In COLT, 2009.
[121] Tsendsuren Munkhdalai and Hong Yu. Meta networks. In ICML, 2017.
[122] Jiquan Ngiam, Daiyi Peng, Vijay Vasudevan, Simon Kornblith, Quoc V Le, and Ruoming Pang. Domain adaptive transfer learning with specialist models. arXiv preprint arXiv:1811.07056, 2018.
[123] Cuong Nguyen, Tal Hassner, Matthias Seeger, and Cedric Archambeau. Leep: A new measure to evaluate transferability of learned representations. In ICML, 2020.
[124] Aaron van den Oord, Yazhe Li, and Oriol Vinyals. Representation learning with contrastive predictive coding. NeurIPS, 2019.
[125] Sinno Jialin Pan and Qiang Yang. A survey on transfer learning. TKDE, pages 1345–1359, 2010.
[126] Sinno Jialin Pan, Ivor W. Tsang, James T. Kwok, and Qiang Yang. Domain adaptation via transfer component analysis. TNNLS, pages 199–210, 2011.
[127] Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, Alban Desmaison, Andreas Kopf, Edward Yang, Zachary DeVito, Martin Raison, Alykhan Tejani, Sasank Chilamkurthy, Benoit Steiner, Lu Fang, Junjie Bai, and Soumith Chintala. Pytorch: An imperative style, high-performance deep learning library. In NeurIPS, 2019.
[128] Xingchao Peng, Qinxun Bai, Xide Xia, Zijun Huang, Kate Saenko, and Bo Wang. Moment matching for multi-source domain adaptation. In ICCV, 2019.
[129] Jonas Peters, Peter B¨uhlmann, and Nicolai Meinshausen. Causal inference by using invariant prediction: identification and confidence intervals. Journal of the Royal Statistical Society. Series B (Statistical Methodology), pages 947–1012, 2016.
[130] Jonas Peters, Dominik Janzing, and Bernhard Sch¨olkopf. Elements of causal inference: foundations and learning algorithms. The MIT Press, 2017.
[131] Matthew E Peters, Mark Neumann, Mohit Iyyer, Matt Gardner, Christopher Clark, Kenton Lee, and Luke Zettlemoyer. Deep contextualized word representations. In NAACL, 2018.
[132] Telmo Pires, Eva Schlinger, and Dan Garrette. How multilingual is multilingual bert? In ACL, 2019.
[133] J. Quionero-Candela, M. Sugiyama, A. Schwaighofer, and N. D. Lawrence. Dataset shift in machine learning. The MIT Press, 2009.
[134] Alec Radford, Karthik Narasimhan, Tim Salimans, and Ilya Sutskever. Improving language understanding by generative pre-training. Technical report, OpenAI, 2018.
[135] Alec Radford, Jong Wook Kim, Chris Hallacy, Aditya Ramesh, Gabriel Goh, Sandhini Agarwal, Girish Sastry, Amanda Askell, Pamela Mishkin, Jack Clark, et al. Learning transferable visual models from natural language supervision. In ICML, 2021.
[136] Colin Raffel, Noam Shazeer, Adam Roberts, Katherine Lee, Sharan Narang, Michael Matena, Yanqi Zhou, Wei Li, and Peter J Liu. Exploring the limits of transfer learning with a unified text-to-text transformer. JMLR, 21(140):1–67, 2020.
[137] Aniruddh Raghu, Maithra Raghu, Samy Bengio, and Oriol Vinyals. Rapid learning or feature reuse? towards understanding the effectiveness of maml. In ICLR, 2020.
[138] Maithra Raghu, Chiyuan Zhang, Jon Kleinberg, and Samy Bengio. Transfusion: Understanding transfer learning for medical imaging. In NeurIPS, 2019.
[139] S-A Rebuffi, H. Bilen, and A. Vedaldi. Learning multiple visual domains with residual adapters. In NeurIPS, 2017.
[140] Ievgen Redko, Emilie Morvant, Amaury Habrard, Marc Sebban, and Youn`es Bennani. A survey on domain adaptation theory: learning bounds and theoretical guarantees, 2020.
[141] Shaoqing Ren, Kaiming He, Ross Girshick, and Jian Sun. Faster r-cnn: Towards real-time object detection with region proposal networks. In NeurIPS, 2015.
[142] Michael T. Rosenstein. To transfer or not to transfer. In NeurIPS, 2005.
[143] Evgenia. Rusak, Steffen Schneider, Peter Gehler, Oliver Bringmann, Wieland Brendel, and Matthias Bethge. Adapting imagenet-scale models to complex distribution shifts with self-learning. arXiv preprint arXiv:2104.12928, 2021.
[144] Olga Russakovsky, Jia Deng, Hao Su, Jonathan Krause, Sanjeev Satheesh, Sean Ma, Zhiheng Huang, Andrej Karpathy, Aditya Khosla, Michael Bernstein, Alexander C. Berg, and Li Fei-Fei. ImageNet Large Scale Visual Recognition Challenge. IJCV, 115(3):211– 252, 2015.
[145] Andrei A Rusu, Dushyant Rao, Jakub Sygnowski, Oriol Vinyals, Razvan Pascanu, Simon Osindero, and Raia Hadsell. Meta-learning with latent embedding optimization. In ICLR, 2019.
[146] Kuniaki Saito, Kohei Watanabe, Yoshitaka Ushiku, and Tatsuya Harada. Maximum classifier discrepancy for unsupervised domain adaptation. In CVPR, 2018.
[147] Kuniaki Saito, Yoshitaka Ushiku, Tatsuya Harada, and Kate Saenko. Strong-weak distribution alignment for adaptive object detection. In CVPR, 2019.
[148] Hadi Salman, Andrew Ilyas, Logan Engstrom, Ashish Kapoor, and Aleksander Madry. Do adversarially robust imagenet models transfer better? In NeurIPS, 2020.
[149] Swami Sankaranarayanan, Yogesh Balaji, Carlos D. Castillo, and Rama Chellappa. Generate to adapt: Aligning domains using generative adversarial networks. In CVPR, 2018.
[150] Adam Santoro, Sergey Bartunov, Matthew Botvinick, Daan Wierstra, and Timothy Lillicrap. Meta-learning with memory-augmented neural networks. In ICML, 2016.
[151] Timo Schick and Hinrich Sch¨utze. Exploiting cloze questions for few-shot text classification and natural language inference. In EACL, 2020.
[152] J¨urgen Schmidhuber. Evolutionary principles in self-referential learning. PhD thesis, Technische Universit¨at M¨unchen, 1987.
[153] Bernhard Sch¨olkopf, Dominik Janzing, Jonas Peters, Eleni Sgouritsa, Kun Zhang, and Joris Mooij. On causal and anticausal learning. In ICML, 2012.
[154] Bernhard Sch¨olkopf, Francesco Locatello, Stefan Bauer, Nan Rosemary Ke, Nal Kalchbrenner, Anirudh Goyal, and Yoshua Bengio. Toward causal representation learning. Proceedings of the IEEE, 109(5):612–634, 2021.
[155] Andrew W Senior, Richard Evans, John Jumper, James Kirkpatrick, Laurent Sifre, Tim Green, Chongli Qin, Augustin ˇZ´ıdek, Alexander WR Nelson, Alex Bridgland, et al. Improved protein structure prediction using potentials from deep learning. Nature, 577 (7792):706–710, 2020.
[156] Pierre Sermanet, David Eigen, Xiang Zhang, Micha¨el Mathieu, Rob Fergus, and Yann LeCun. Overfeat: Integrated recognition, localization and detection using convolutional networks. arXiv preprint arXiv:1312.6229, 2013.
[157] Ashish Shrivastava, Tomas Pfister, Oncel Tuzel, Josh Susskind, Wenda Wang, and Russell Webb. Learning from simulated and unsupervised images through adversarial training. In CVPR, 2017.
[158] Rui Shu, Hung H. Bui, Hirokazu Narui, and Stefano Ermon. A dirt-t approach to unsupervised domain adaptation. In ICLR, 2018.
[159] Yang Shu, Zhangjie Cao, Jinghan Gao, Jianmin Wang, and Mingsheng Long. Omni-training for data-efficient deep learning. arXiv preprint arXiv:2110.07510, 2021a.
[160] Yang Shu, Zhi Kou, Zhangjie Cao, Jianmin Wang, and Mingsheng Long. Zoo-tuning: Adaptive transfer from a zoo of models. In ICML, 2021b.
[161] David Silver, Aja Huang, Chris J Maddison, Arthur Guez, Laurent Sifre, George Van Den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, et al. Mastering the game of go with deep neural networks and tree search. Nature, 529(7587):484–489, 2016.
[162] Jake Snell, Kevin Swersky, and Richard S. Zemel. Prototypical networks for few-shot learning. In NeurIPS, 2017.
[163] Bharath K. Sriperumbudur, Arthur Gretton, Kenji Fukumizu, Bernhard Sch¨olkopf, and Gert R. G. Lanckriet. Hilbert space embeddings and metrics on probability measures. JMLR, 2010.
[164] Masashi Sugiyama, Matthias Krauledat, and Klaus-Robert M¨uller. Covariate shift adaptation by importance weighted cross validation. JMLR, 8(35):985–1005, 2007.
[165] Masashi Sugiyama, Shinichi Nakajima, Hisashi Kashima, Paul Buenau, and Motoaki Kawanabe. Direct importance estimation with model selection and its application to covariate shift adaptation. In NeurIPS, 2008.
[166] Baochen Sun and Kate Saenko. Deep coral: Correlation alignment for deep domain adaptation. In ECCV, 2016.
[167] Qianru Sun, Yaoyao Liu, Tat-Seng Chua, and Bernt Schiele. Meta-transfer learning for few-shot learning. In CVPR, 2019a.
[168] Yu Sun, Shuohuan Wang, Yukun Li, Shikun Feng, Xuyi Chen, Han Zhang, Xin Tian, Danxiang Zhu, Hao Tian, and Hua Wu. Ernie: Enhanced representation through knowledge integration. arXiv preprint arXiv:1904.09223, 2019b.
[169] Yaniv Taigman, Adam Polyak, and Lior Wolf. Unsupervised cross-domain image generation. In ICLR, 2017.
[170] Sebastian Thrun and Lorien Pratt. Learning to learn. Springer Science & Business Media, 1998.
[171] Yonglong Tian, Dilip Krishnan, and Phillip Isola. Contrastive multiview coding. In ECCV, 2020.
[172] Lisa Torrey and Jude Shavlik. Transfer learning. 2010.
[173] Yi-Hsuan Tsai, Wei-Chih Hung, Samuel Schulter, Kihyuk Sohn, Ming-Hsuan Yang, and Manmohan Chandraker. Learning to adapt structured output space for semantic segmentation. In CVPR, 2018.
[174] Eric Tzeng, Judy Hoffman, Ning Zhang, Kate Saenko, and Trevor Darrell. Deep domain confusion: Maximizing for domain invariance. 2014.
[175] Eric Tzeng, Judy Hoffman, Trevor Darrell, and Kate Saenko. Simultaneous deep transfer across domains and tasks. In ICCV, pages 4068–4076, 2015.
[176] Eric Tzeng, Judy Hoffman, Kate Saenko, and Trevor Darrell. Adversarial discriminative domain adaptation. In CVPR, 2017.
[177] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, �Lukasz Kaiser, and Illia Polosukhin. Attention is all you need. In NeurIPS, 2017.
[178] Petar Veliˇckovi´c, William Fedus, William L Hamilton, Pietro Li`o, Yoshua Bengio, and R Devon Hjelm. Deep graph infomax. In ICLR, 2019.
[179] Pascal Vincent, Hugo Larochelle, Yoshua Bengio, and Pierre-Antoine Manzagol. Extracting and composing robust features with denoising autoencoders. In ICML, 2008.
[180] Oriol Vinyals, Charles Blundell, Timothy Lillicrap, Daan Wierstra, et al. Matching networks for one shot learning. In NeurIPS, 2016.
[181] Oriol Vinyals, Igor Babuschkin, Wojciech M Czarnecki, Micha¨el Mathieu, Andrew Dudzik, Junyoung Chung, David H Choi, Richard Powell, Timo Ewalds, Petko Georgiev, et al. Grandmaster level in starcraft ii using multi-agent reinforcement learning. Nature, 575 (7782):350–354, 2019.
[182] Tuan-Hung Vu, Himalaya Jain, Maxime Bucher, Matthieu Cord, and Patrick Perez. Advent: Adversarial entropy minimization for domain adaptation in semantic segmentation. In CVPR, 2019.
[183] Alex Wang, Amanpreet Singh, Julian Michael, Felix Hill, Omer Levy, and Samuel R. Bowman. GLUE: A multi-task benchmark and analysis platform for natural language understanding. In ICLR, 2019a.
[184] Haohan Wang, Songwei Ge, Zachary Lipton, and Eric P Xing. Learning robust global representations by penalizing local predictive power. In NeurIPS, 2019b.
[185] Ximei Wang, Ying Jin, Mingsheng Long, Jianmin Wang, and Michael I Jordan. Transferable normalization: Towards improving transferability of deep neural networks. In NeurIPS, 2019c.
[186] Ximei Wang, Jinghan Gao, Mingsheng Long, and Jianmin Wang. Self-tuning for dataefficient deep learning. In ICML, 2021.
[187] Zirui Wang, Zihang Dai, Barnab´as P´oczos, and Jaime G. Carbonell. Characterizing and avoiding negative transfer. In CVPR, 2019d.
[188] Jason Wei, Maarten Bosma, Vincent Y. Zhao, Kelvin Guu, Adams Wei Yu, Brian Lester, Nan Du, Andrew M. Dai, and Quoc V. Le. Finetuned language models are zero-shot learners. In ICLR, 2022.
[189] Longhui Wei, Shiliang Zhang, Wen Gao, and Qi Tian. Person transfer gan to bridge domain gap for person re-identification. In CVPR, 2018.
[190] Ross Wightman. Pytorch image models. https://github.com/rwightman/ pytorch-image-models, 2019.
[191] Yuxin Wu and Kaiming He. Group normalization. In ECCV, 2018.
[192] Zhirong Wu, Yuanjun Xiong, X Yu Stella, and Dahua Lin. Unsupervised feature learning via non-parametric instance discrimination. In CVPR, 2018.
[193] Runxin Xu, Fuli Luo, Zhiyuan Zhang, Chuanqi Tan, Baobao Chang, Songfang Huang, and Fei Huang. Raise a child in large language model: Towards effective and generalizable fine-tuning. In EMNLP, 2021.
[194] I Zeki Yalniz, Herv´e J´egou, Kan Chen, Manohar Paluri, and Dhruv Mahajan. Billion-scale semi-supervised learning for image classification. arXiv preprint arXiv:1905.00546, 2019.
[195] Zhilin Yang, Zihang Dai, Yiming Yang, Jaime Carbonell, Russ R Salakhutdinov, and Quoc V Le. Xlnet: Generalized autoregressive pretraining for language understanding. In NeurIPS, 2019.
[196] Huaxiu Yao, Ying Wei, Junzhou Huang, and Zhenhui Li. Hierarchically structured metalearning. In ICML, 2019.
[197] Jason Yosinski, Jeff Clune, Yoshua Bengio, and Hod Lipson. How transferable are features in deep neural networks? In NeurIPS, 2014.
[198] Kaichao You, Yong Liu, Jianmin Wang, and Mingsheng Long. Logme: Practical assessment of pre-trained models for transfer learning. In ICML, 2021.
[199] Amir Roshan Zamir, Alexander Sax, William B. Shen, Leonidas J. Guibas, Jitendra Malik, and Silvio Savarese. Taskonomy: Disentangling task transfer learning. In CVPR, 2018.
[200] Werner Zellinger, Thomas Grubinger, Edwin Lughofer, Thomas Natschl¨ager, and Susanne Saminger-Platz. Central moment discrepancy (cmd) for domain-invariant representation learning. In ICLR, 2017.
[201] Chiyuan Zhang, Samy Bengio, Moritz Hardt, Benjamin Recht, and Oriol Vinyals. Understanding deep learning requires rethinking generalization. In ICLR, 2017.
[202] Hongyang Zhang, Yaodong Yu, Jiantao Jiao, Eric P. Xing, Laurent El Ghaoui, and Michael I. Jordan. Theoretically principled trade-off between robustness and accuracy. In ICML, 2019a.
[203] Jeffrey O. Zhang, Alexander Sax, Amir Zamir, Leonidas J. Guibas, and Jitendra Malik. Side-tuning: Network adaptation via additive side networks. 2019b.
[204] Yuchen Zhang, Tianle Liu, Mingsheng Long, and Michael Jordan. Bridging theory and algorithm for domain adaptation. In ICML, 2019c.
[205] Zhilu Zhang and Mert R. Sabuncu. Generalized cross entropy loss for training deep neural networks with noisy labels. In NeurIPS, 2018.
[206] Nanxuan Zhao, Zhirong Wu, Rynson W. H. Lau, and Stephen Lin. What makes instance discrimination good for transfer learning? In ICLR, 2021.
[207] Lucia Zheng, Neel Guha, Brandon R. Anderson, Peter Henderson, and Daniel E. Ho. When does pretraining help? assessing self-supervised learning for law and the casehold dataset. In ICAIL, 2021.
[208] Jincheng Zhong, Ximei Wang, Zhi Kou, Jianmin Wang, and Mingsheng Long. Bi-tuning of pre-trained representations. arXiv preprint arXiv:2011.06182, 2020.
[209] Jun-Yan Zhu, Taesung Park, Phillip Isola, and Alexei A Efros. Unpaired image-to-image translation using cycle-consistent adversarial networks. In ICCV, 2017.
[210] Yukun Zhu, Ryan Kiros, Rich Zemel, Ruslan Salakhutdinov, Raquel Urtasun, Antonio Torralba, and Sanja Fidler. Aligning books and movies: Towards story-like visual explanations by watching movies and reading books. In ICCV, 2015.
[211] Fuzhen Zhuang, Zhiyuan Qi, Keyu Duan, Dongbo Xi, Yongchun Zhu, Hengshu Zhu, Hui Xiong, and Qing He. A comprehensive survey on transfer learning. Proceedings of the IEEE, 109(1):43–76, 2021.
[212] Yang Zou, Zhiding Yu, B. V. K. Vijaya Kumar, and Jinsong Wang. Unsupervised domain adaptation for semantic segmentation via class-balanced self-training. In ECCV, 2018.
边栏推荐
- Bootloader implementation of PIC MCU
- Record the opening ceremony of Beijing Winter Olympics with display equipment
- Nb-iot technical summary
- Train your dataset with yolov4
- Programming knowledge -- basis of C language
- Pointnet++ classification practice
- L'étude a révélé que le système de service à la clientèle du commerce électronique transfrontalier a ces cinq fonctions!
- List of linked lists
- Explain task scheduling based on Cortex-M3 in detail (Part 1)
- 生产中影响滑环质量的因素
猜你喜欢
Markdown tips
Management and use of DokuWiki (supplementary)
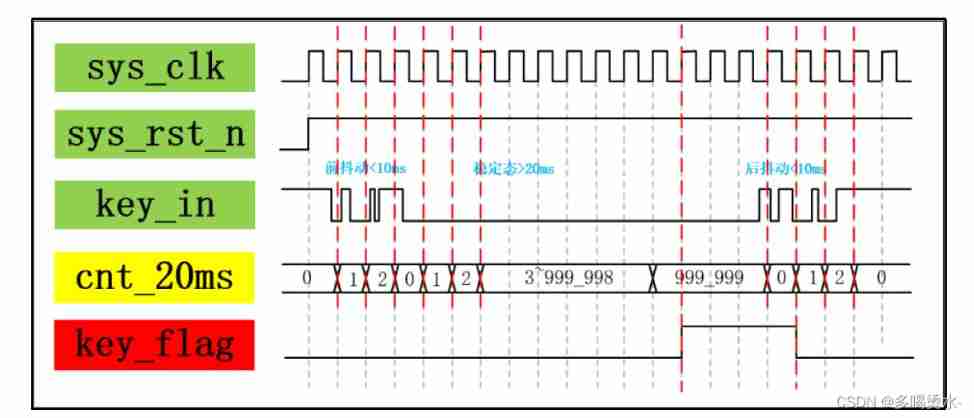
Hardware and software solution of FPGA key chattering elimination
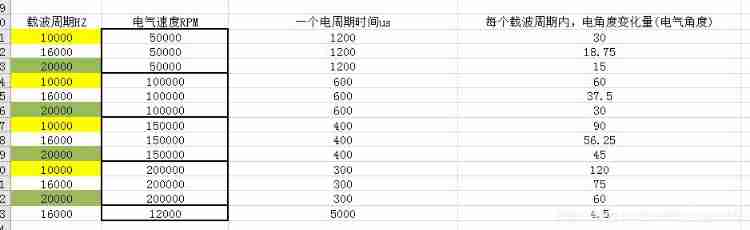
Carrier period, electrical speed, carrier period variation
![[trio basic tutorial 17 from getting started to mastering] set up and connect the trio motion controller and input the activation code](/img/58/576b6b77509ed7a9bef138f3899e37.jpg)
[trio basic tutorial 17 from getting started to mastering] set up and connect the trio motion controller and input the activation code

【论文阅读】2022年最新迁移学习综述笔注(Transferability in Deep Learning: A Survey)
Altium designer learning (I)
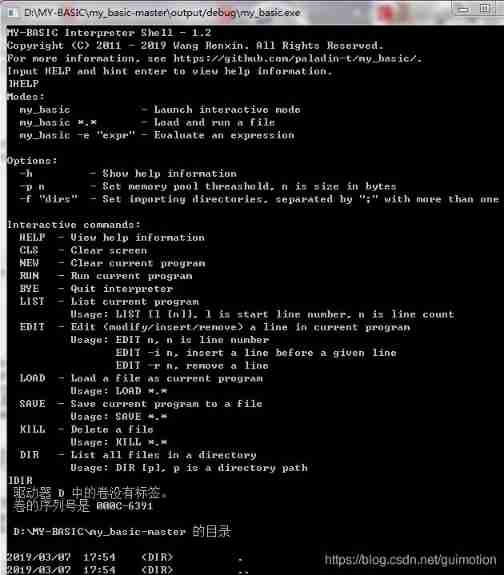
My-basic application 2: my-basic installation and operation

Reasons for rapid wear of conductive slip rings
【云原生 | 从零开始学Kubernetes】三、Kubernetes集群管理工具kubectl
随机推荐
C, Numerical Recipes in C, solution of linear algebraic equations, LU decomposition source program
Shell script basic syntax
Why is 1900 not a leap year
Ads usage skills
Drive LED -- GPIO control
Shape template matching based on Halcon learning [9] PM_ multiple_ dxf_ models. Hdev routine -- [read and write XLD from DXF file]
Measurement fitting based on Halcon learning [i] fuse Hdev routine
List of linked lists
导电滑环磨损快的原因
Problem solving: interpreter error: no file or directory
Soem EtherCAT source code analysis attachment 1 (establishment of communication operation environment)
Vofa+ software usage record
Shell脚本基本语法
Explain task scheduling based on Cortex-M3 in detail (Part 2)
Random function usage notes
Network port usage
Count and sort the occurrence times of specific fields through SQL statements
Sql Server的存储过程详解
C WinForm [view status bar -- statusstrip] - Practice 2
The firmware of the connected j-link does not support the following memory access