当前位置:网站首页>Figure application details
Figure application details
2022-07-06 04:09:00 【ZNineSun】
List of articles
The application of graph mainly includes : Minimum generation ( cost ) Trees 、 Shortest path 、 Topological sorting and
critical path , It plays an important role in data structure , There are many algorithms involved , It's also important. , I hope you can master all through this article .
1. Minimum spanning tree
Before we know the minimum spanning tree , You should first know what a spanning tree is ?
Make trees : All tops are linked together by edges , But there is no diagram of the loop .
Spanning tree has the following characteristics :
- A loop will appear on one more side
- Missing an edge will lead to vertices that cannot be linked
- A graph can have many different spanning trees
As shown in the figure below :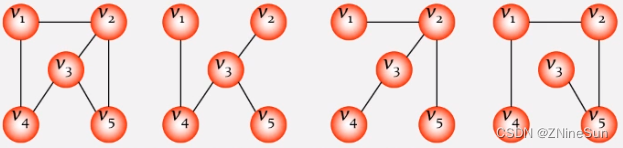
I know what a spanning tree is , In understanding what is called minimum spanning tree
1.2 Minimum spanning tree
Given an undirected network , Then all spanning trees of the network , The spanning tree that minimizes the sum of the weights of each edge is called the minimum spanning tree of the network , Also called Minimum cost spanning tree .
1.3 Minimum spanning tree usage
- in n Establish a communication network between two cities , stay n Shops in cities n-1 line ;
- But because each line will have the corresponding economic cost , and n Cities have at most n*(n-1)/2 line , that , How to choose n-1 line , To minimize the total cost ?
1.4 How to build a minimum spanning tree
There are two main algorithms for building minimum spanning trees ,Prim Algorithm 、Kruskal Algorithm , They are all strategies based on greedy algorithms , Let me explain them one by one .
1.4.1 Prim Algorithm
Initially, take any vertex from the graph and add it to the tree T, There is only one vertex in the tree , Then select one that is related to the current T The nearest vertex in the vertex set , And add the vertex and the corresponding edge T, After each operation T The number of vertices and edges in both increase 1, By analogy , Until all vertices in the graph are added T in , The whole process is shown in the figure below :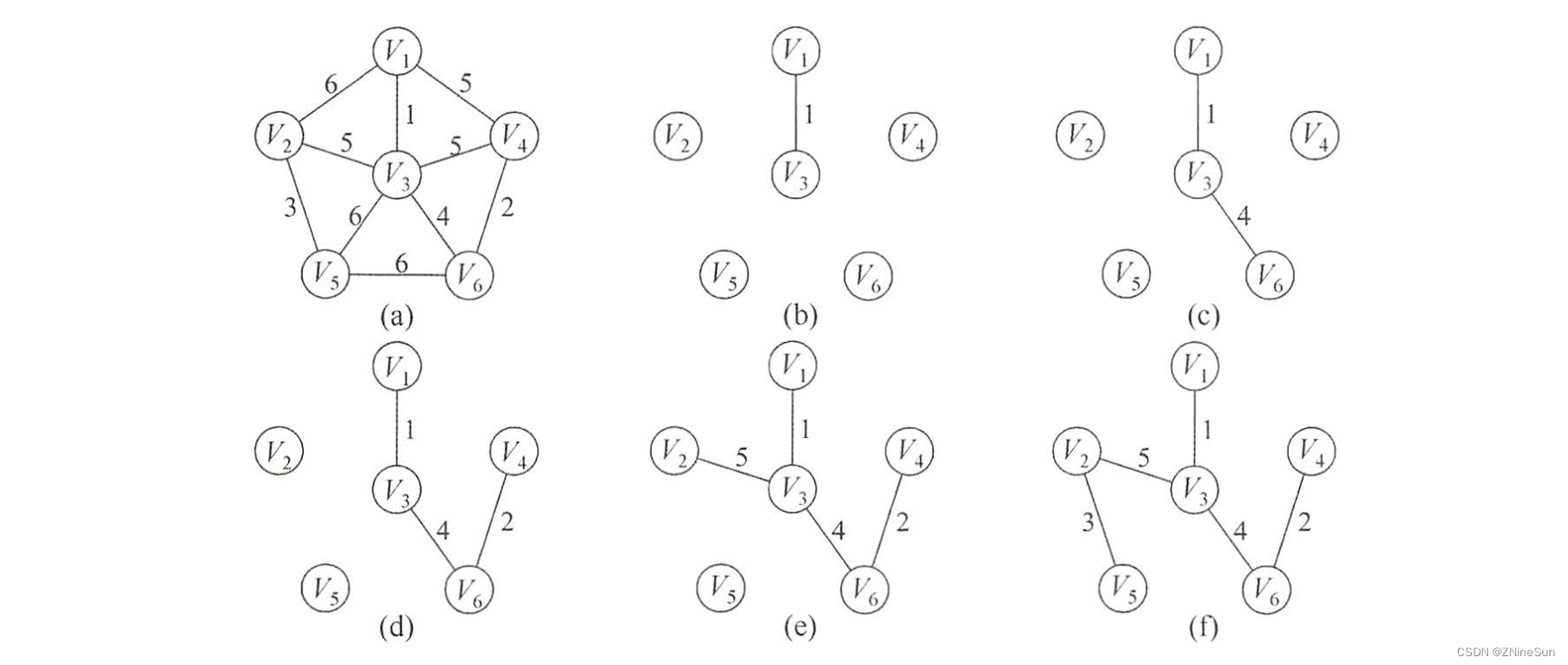
The code implementation is as follows :(Java edition )
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/** * Prim The idea of the algorithm is to take any vertex on the way i As starting point , And add it to S Collection . from V-S(V Represents all vertices ) The collection of * Select one to S The shortest edge of the vertex of the set . for example S There are (1,2) Two vertices ,V-S There are (4,5,6) Three vertices , that * take (1,4) (1,5) (1,6) (2,4) (2,5) (2,6) The smallest of the six sides , If (1,4) This edge has the smallest weight , that * take 4 This vertex is added S in . By analogy , until S The number of is equal to the number of all vertices n. */
public class Prim {
//flag Mark which path is selected , for example :flag[1][2] = true Then it indicates that from 1 To 2 This path has been selected
// data c[i][j] From i To j A weight ,n Indicates how many vertices there are in a
public void prim(int[][] c, int n,boolean[][] flag) {
List<Integer> list = new ArrayList<>();
int start = 0,end = 0,min = Integer.MAX_VALUE;
// Mark which path is selected , for example :flag[1][2] = true Then it indicates that from 1 To 2 This path has been selected
// The starting point is set to 0, Next, traverse to find out from 0 The shortest way to go
for (int i = 1; i < n; i++) {
if (c[0][i] < min){
start = 0;
end = i;
min = c[0][1];
}
}
list.add(0);
// take (0,i) The vertex of the edge with the smallest weight is added to list in
list.add(end);
// Mark the path taken
flag[0][end] = true;
while (list.size() != n){
min = Integer.MAX_VALUE;
// from V-S(V Represents all vertices ) Select one from the set of to S The shortest edge of the vertex of the set
for (Integer i: list) {
for (int j = 0 ; j < n; j++){
if (!flag[i][j] && !list.contains(j) && c[i][j] < min){
start = i;
end = j;
min = c[i][j];
}
}
}
flag[start][end] = true;
list.add(end);
}
}
}
Prim The time complexity of the algorithm is O(|V|^2), Don't depend on |E|), Therefore, it is suitable for solving the minimum spanning tree of graphs with dense edges .
Although using other methods can improve Prim The time complexity of the algorithm , But it increases the complexity of the implementation .
1.4.2 KrusKal Algorithm
And Prim The algorithm extends the minimum spanning tree from the vertex ,Kruskal ( Kruskar ) The algorithm is a method of selecting appropriate edges to construct a minimum spanning tree according to the increasing order of weights .
I will not introduce the process here , The words are complex and difficult to understand , Let's look at it directly through the flow chart :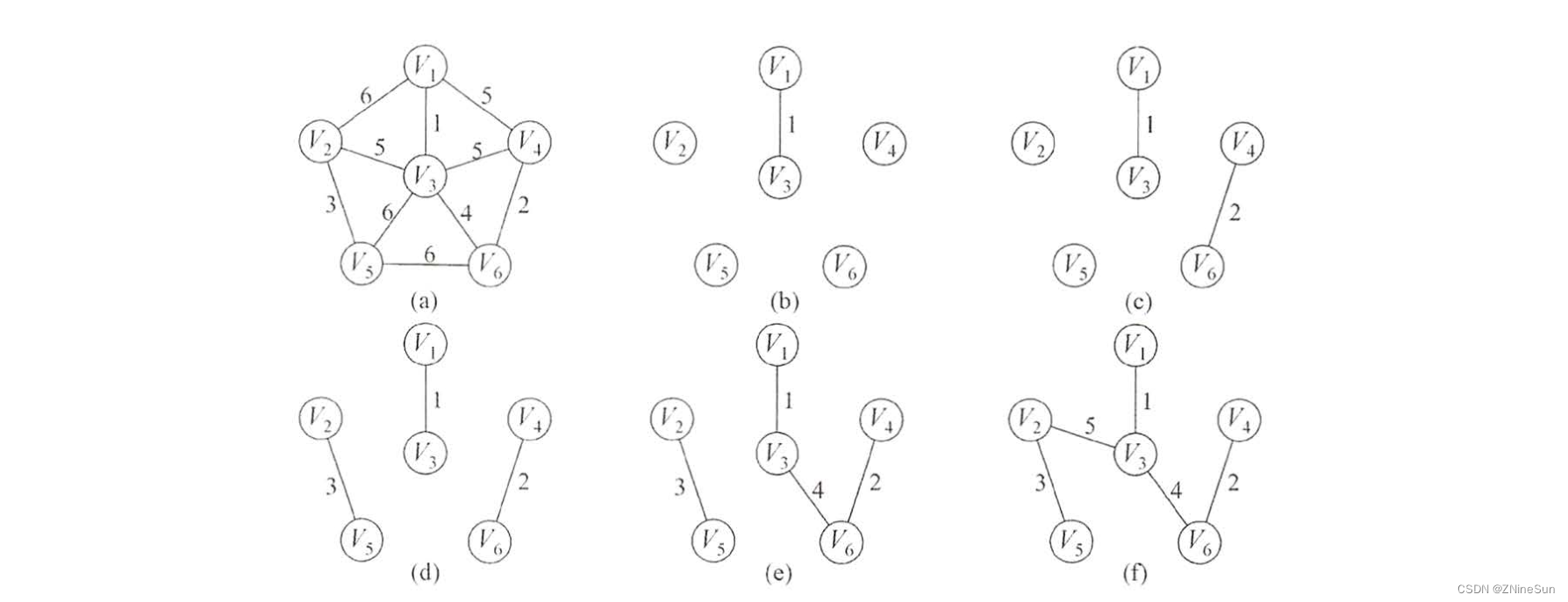
As can be seen from the figure above , Each time, the side with the least cost is selected .
According to the relevant properties of graphs , If an edge connects vertices in two different trees , For these two trees , It must be connected , Add this side to the forest , Complete the merging of the two trees ,
Until the whole forest merges into a tree .
Usually in Kruskal In the algorithm, , Heap is used to store the collection of edges , Therefore, each time you select the edge with the minimum weight, you only need O(log|E|) Time for . Besides , Because spanning tree T All edges in can be regarded as an equivalent class , Therefore, the process of adding new edges each time is similar to the process of solving equivalence classes , Therefore, we can use the data structure of joint search set to describe T, Thus construct T The time complexity of is O(Elog|E|). therefore ,Kruskal The algorithm is suitable for Sparse edges and many vertices Graph .
ps: Recommended articles
2. Shortest path
We may know that breadth first search can find the shortest path , Breadth first I don't know about , Breadth first search is essentially hierarchical traversal , At the same time, breadth first search to find the shortest path is only for the unauthorized graph .
When the graph is weighted , Take it from a vertex v0 To any other vertex in the graph v1 A path for ( There may be more than one ) The sum of the weights on the edges passed , Defined as the weighted path length of the path , The path with the shortest length of the weighted path is called Shortest path .
The algorithm for solving the shortest path usually depends on one property , That is, the shortest path between two points also includes the shortest path between other vertices on the path .
Weighted digraphs G The shortest path problem of can be generally divided into two categories :
- The first is the single source shortest path
That is to find the shortest path from a vertex in the graph to other vertices , It can be done through the classic Dijkstra( dijkstra ) Algorithmic solution ; - The second is to find the shortest path between each pair of vertices
It can be done by Floyd( Freud ) Algorithm to solve .
2.1 Dijkstra Solve the single source shortest path problem
Dijkstra The algorithm sets a set S Record the vertices of the shortest path obtained , Initially, put the source point v0 Join in S, aggregate S Every time you merge into a new vertex v, You have to modify the source point v0 To the assembly V-S The current shortest path length value of the vertex in the ( It may not be easy to understand here ? No problem , It will be clear later ).
We still have the old rules , Start with the flow of the algorithm :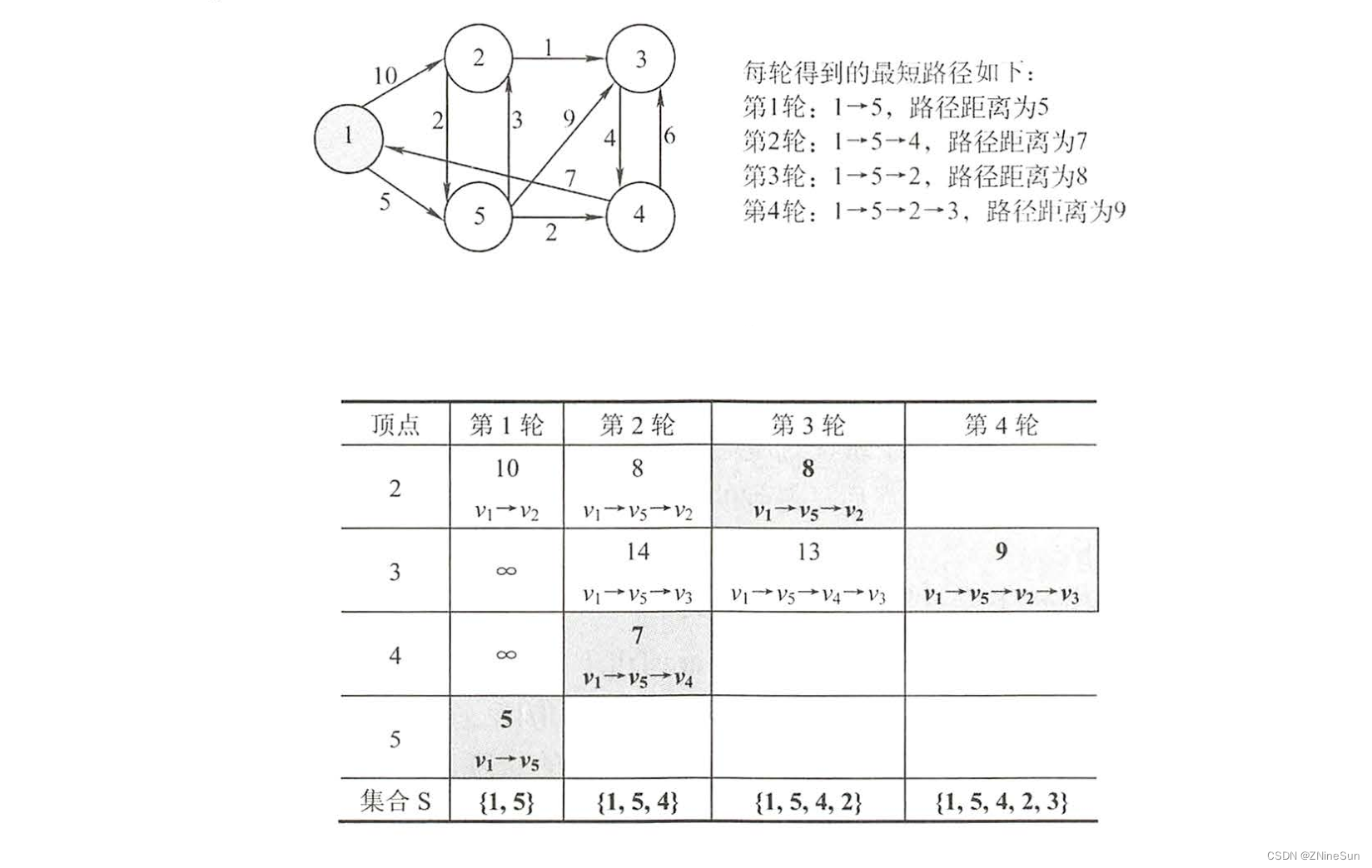
We can see from the picture above , Each round will choose a shortest path , Then add vertices to the set S in .
- The first round :v1->v5 The shortest ,S Are there in :{v1,v5}
- The second round : Put all the v1,v5 The nodes that can be reached should be taken into account , And choose the shortest path , As can be seen from the picture v1->v5->v4 Is the shortest path of the second round , At this time, put v4 Add to set S, here S Are there in :{v1,v5,v4}
- The third round : Put all the v1,v5,v4 The nodes that can be reached should be taken into account , And choose the shortest path , As can be seen from the picture v1->v5->v2 It is the shortest path of the third round , At this time, put v2 Add to set S, here S Are there in :{v1,v5,v4,v2}
- The fourth round , Put all the v1,v5,v4,v2 The nodes that can be reached should be taken into account , And choose the shortest path , As can be seen from the picture v1->v5->v2->v3 It is the shortest path of the fourth round , At this time, put v3 Add to set S, here S Are there in :{v1,v5,v4,v2,v3}
So far, all nodes have joined .
It is not difficult to see from the above process ,Dijkstra The algorithm is also based on greedy strategy .
3. A topological sort
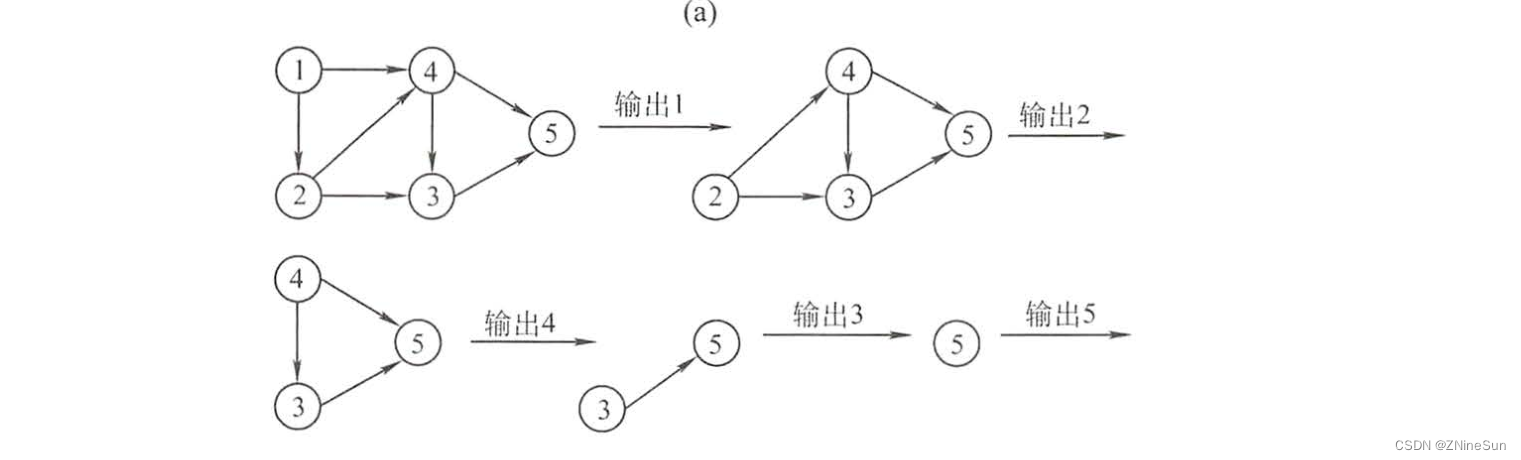
The above figure clearly describes the process of topological sorting , That is, choose one degree each time for 0 Point output of , Then delete the vertex , And the directed edge starting from it .
4. critical path
stay AOE In the net , Some activities can be carried out in parallel . There may be more than one directed path from the source point to the sink point , And the length of these paths may be different . The time required to complete activities on different paths is different , But only the activities on all paths have been completed , The whole project can be regarded as finished . therefore , In all paths from source to sink , The path with the maximum path length is called critical path , The activities on the critical path are called critical activities .
The shortest time to complete the whole project is the length of the critical path , That is, the total cost of each activity on the critical path . This is because key activities affect the time of the whole project , That is, if key activities cannot be completed on time , The completion time of the whole project will be extended . therefore , As long as we find the key activities , We found the critical path , Then we can get the shortest completion time .
Let's start with a few definitions , Maybe you look at these now The definition is rather obscure , It doesn't matter. , I'll give you an example later to help you understand .
- event vK The earliest occurrence time of :ve(k)
ve(k)=Max{ve(j)+Weight(vj,vk)}
among :vk Is for vj The successor node of ,Weight(vj,vk) yes vj-vk The weight of
Is it hard to understand , No problem , You just need to remember to use Maximum Just fine
- Time vk The latest time of occurrence of :vl(k)
vl(k)=Min{vl(j)-Weight(vk,vj)}
Again Just remember our requirements vl, Need to use minimum value
- Activities ai The earliest start time of e(i)
It refers to the earliest occurrence time of the event represented by the starting point of the active arc . Ruobian <vk,vj> It means activity a;, Then there are e(i)= ve(k). - Activities ai The latest start time for l(i)
It refers to the difference between the latest occurrence time of the event represented by the end of the active arc and the time required for the activity . Ruobian <vk, vj> It means activity ai, Then there are l(i)= vl(j) - Weight(vk,vj) - An activity ai The latest start time for l(i) And its earliest start time e(i) Difference of d(i)=l(i)-e(i)
di Just for 0, Is part of the critical path
Are you confused , Don't worry , You only need to know these five nouns first .
Give a AOE network , Calculate the AOE The critical path to success :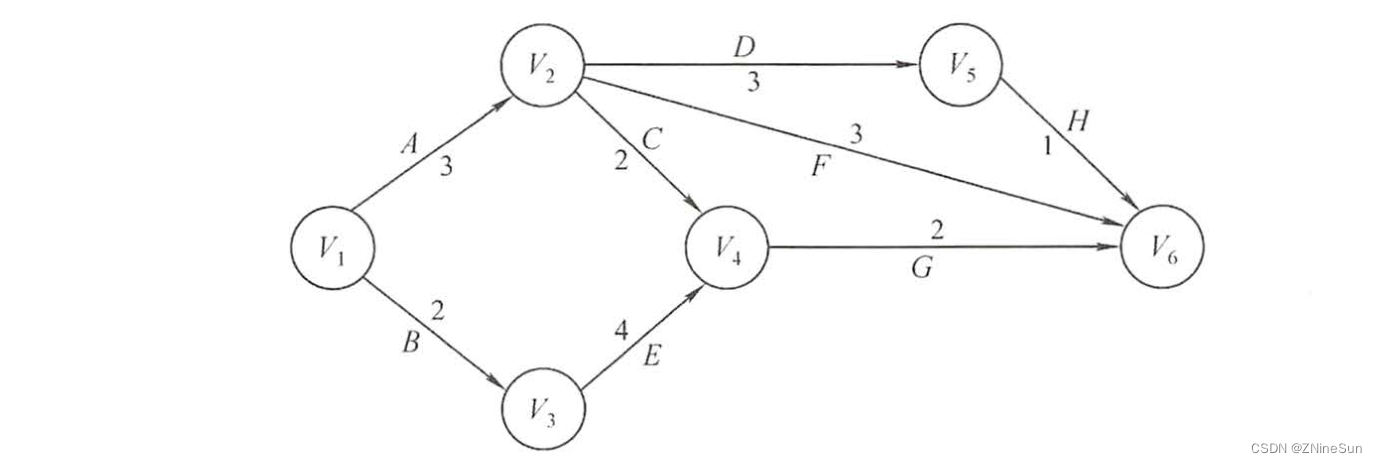
Let's first calculate ve, Through ve Calculation vl
How are these values calculated ?
Let's take a look first ve Calculation process , Remember I said calculation above ve Use the maximum , therefore
- v2 Express :v1->v2 The maximum value of the path , We can see from the picture that only A This path , The path weight is 3, So the data in the table is 3
- v3 Express :v1->v3 Maximum value of path weight , Obviously v1->v3 There is only one path B, The weight of 2, So the result is 2
- v4 Express :v1->v4 Maximum path weight ,v1->v4 There are :v1->v2->v4( The weight result is :5)、v1->v3->v4( The weight result is :6), Taking the maximum , So the result is 6
- v5 Express :v1->v5 Maximum path weight ,v1->v5 There are :v1->v2->v5, Only this one , So the result is 6
- v6 Express :v1->v6 Maximum value of path weight ,v1->v6 There are v1->v2->v5->v6( Weight summation :7)、v1->v2->v6( Weight summation :6)、v1->v2->v4->v6( Weight summation :7)、v1->v3->v4->v6( Weight summation :8), Taking the maximum 8, So the end result is 8
Is it very simple , good , We are going to have a look vl How does it work , Calculation vl We need to look backwards , From v6 Start looking at ,vl(6)=ve(6)=8 Just fill it in
- v5:v5->v6 There is only one way H, So the result is 8-1=7
- v4:v4->v6 There is only one way G, So the result is 8-2=6
- v3:v3->v6 There is only one path and v3->v4->v6, So the result is 8-2-4=2
- v2:v2->v6:v2->v5->v6(8-1-3=4)、v2->v6(8-3=5)、v2->v4->v6(8-2-2=4) Minimum value , So the result is 4
- v1:v1->v2->v5->v6(8-1-3-3=1)、v1->v2->v6(8-3-3=2)、v1->v2->v4->v6(8-2-3-3=0)、v1->v3->v4->v6(8-2-4-2=0), Minimum value 0, So the end result is 0
Next, we use what we just calculated ve and vl Continue to calculate e(i)、l(i)、d(i)
Let's see e(i) How does it work
- A: yes v1->v2 Path between , therefore e(A)=ve(v1)=0
- B: yes v1->v3 Path between , therefore e(B)=ve(v1)=0
- C: yes v2->v4 Path between , therefore e=ve(v2)=3
- D: yes v2->v5 Path between , therefore e(D)=ve(v2)=3
- E: yes v3->v4 Path between , therefore e(E)=ve(v3)=2
- F: yes v2->v6 Path between , therefore e(F)=ve(v2)=3
- G: yes v4->v6 Path between , therefore e(G)=ve(v4)=6
- H: yes v5->v6 Path between , therefore e(H)=ve(v5)=6
Is it right? so easy!!! Our mission is not over yet , Continue to look at l(i) How to get .
- A: yes v1->v2 Path between , therefore l(A)=vl(v2)-Weight(A)=4-3=1
- B: yes v1->v3 Path between , therefore l(B)=vl(v3)-Weight(B)=2-2=0
- C: yes v2->v4 Path between , therefore l=vl(v4)-Weight=6-2=4
- D: yes v2->v5 Path between , therefore l(D)=vl(v5)-Weight(D)=7-3=4
- E: yes v3->v4 Path between , therefore l(E)=vl(v4)-Weight(E)=6-4=2
- F: yes v2->v6 Path between , therefore l(F)=vl(v6)-Weight(F)=8-3=5
- G: yes v4->v6 Path between , therefore l(G)=vl(v6)-Weight(G)=8-2=6
- H: yes v5->v6 Path between , therefore l(H)=vl(v6)-Weight(H)=8-1=7
It's bad now. d(i),d(i) There's nothing to say , Directly to l(i)-e(i) that will do
In the end, we just have to find d(i)=0 The edge of :B、E、G
The corresponding path is :v1->v3->v4->v6
边栏推荐
- 脚本生命周期
- 图应用详解
- DM8 archive log file manual switching
- IDEA编译JSP页面生成的class文件路径
- Yyds dry goods inventory hcie security Day11: preliminary study of firewall dual machine hot standby and vgmp concepts
- [Zhao Yuqiang] deploy kubernetes cluster with binary package
- 10 exemples les plus courants de gestion du trafic istio, que savez - vous?
- ESP32(基于Arduino)连接EMQX的Mqtt服务器上传信息与命令控制
- Use js to complete an LRU cache
- Le compte racine de la base de données MySQL ne peut pas se connecter à distance à la solution
猜你喜欢
Solution to the problem that the root account of MySQL database cannot be logged in remotely
Execution order of scripts bound to game objects

Exchange bottles (graph theory + thinking)
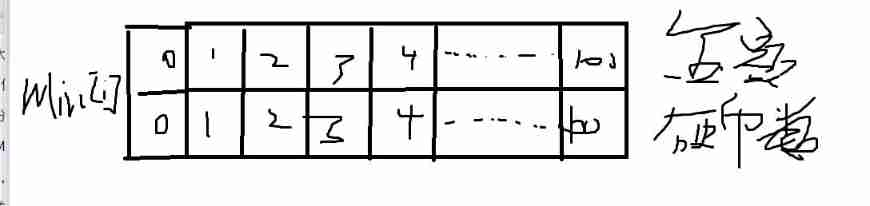
About some basic DP -- those things about coins (the basic introduction of DP)
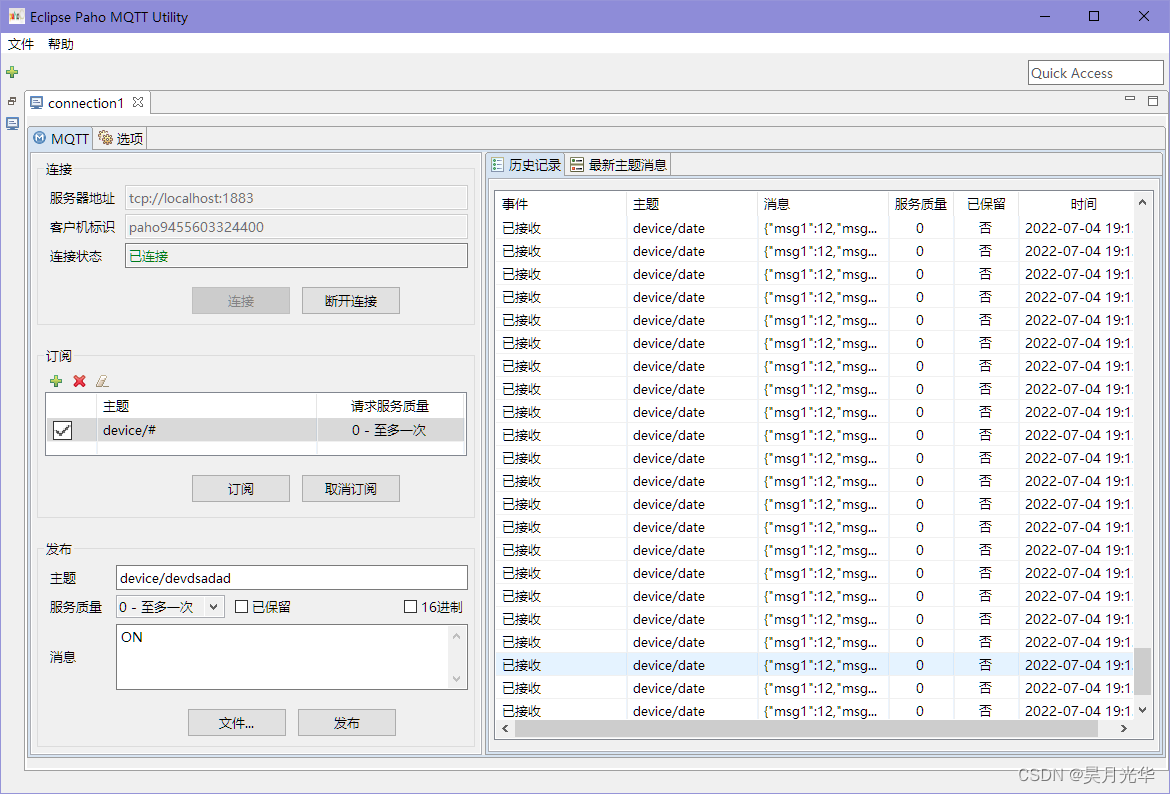
Esp32 (based on Arduino) connects the mqtt server of emqx to upload information and command control

Stc8h development (XII): I2C drive AT24C08, at24c32 series EEPROM storage

ESP32(基于Arduino)连接EMQX的Mqtt服务器上传信息与命令控制
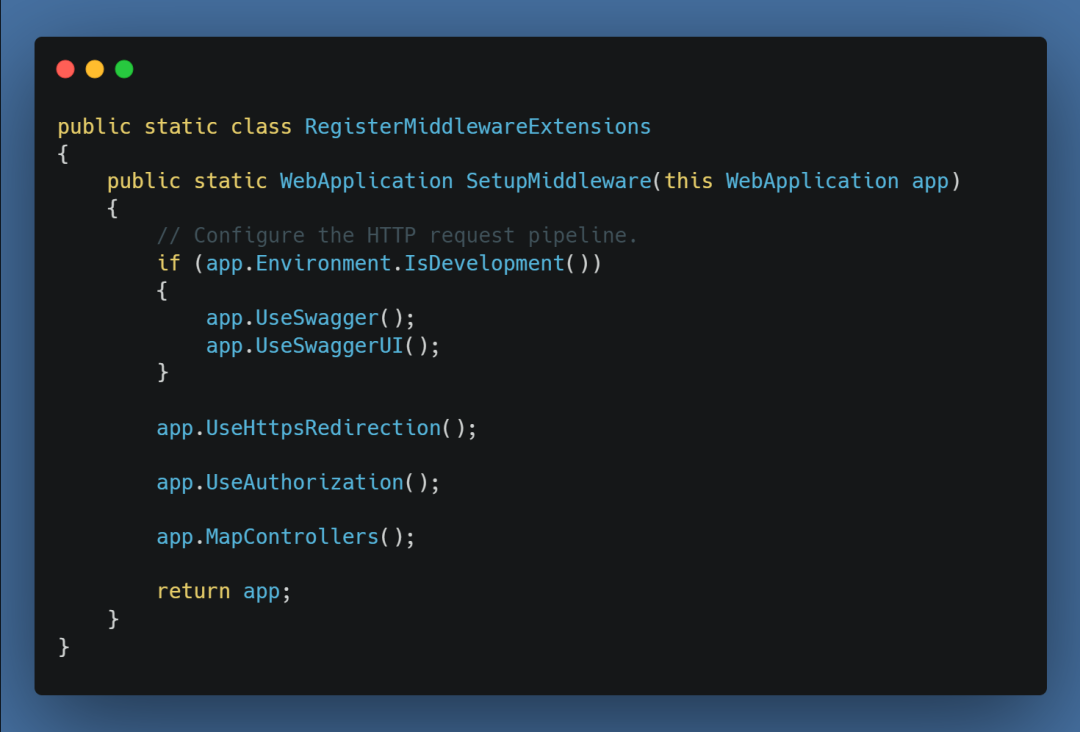
In Net 6 CS more concise method

No qualifying bean of type ‘......‘ available

Le compte racine de la base de données MySQL ne peut pas se connecter à distance à la solution
随机推荐
Global and Chinese market of aircraft anti icing and rain protection systems 2022-2028: Research Report on technology, participants, trends, market size and share
Python book learning notes - Chapter 09 section 01 create and use classes
After five years of testing in byte, I was ruthlessly dismissed in July, hoping to wake up my brother who was paddling
51nod 1130 n factorial length V2 (Stirling approximation)
Exchange bottles (graph theory + thinking)
MySql數據庫root賬戶無法遠程登陸解决辦法
Conditionally [jsonignore]
Lora gateway Ethernet transmission
2/10 parallel search set +bfs+dfs+ shortest path +spfa queue optimization
Facebook and other large companies have leaked more than one billion user data, and it is time to pay attention to did
MySQL about self growth
10個 Istio 流量管理 最常用的例子,你知道幾個?
WPF effect Article 191 box selection listbox
Solution to the problem that the root account of MySQL database cannot be logged in remotely
自动化测试的好处
Benefits of automated testing
C#(二十八)之C#鼠标事件、键盘事件
Maxay paper latex template description
Brief tutorial for soft exam system architecture designer | general catalog
Viewing and verifying backup sets using dmrman