当前位置:网站首页>math_极限&微分&导数&微商/对数函数的导函数推导(导数定义极限法)/指数函数求导公式推导(反函数求导法则/对数求导法)
math_极限&微分&导数&微商/对数函数的导函数推导(导数定义极限法)/指数函数求导公式推导(反函数求导法则/对数求导法)
2022-07-06 03:47:00 【xuchaoxin1375】
微分&导数&微商
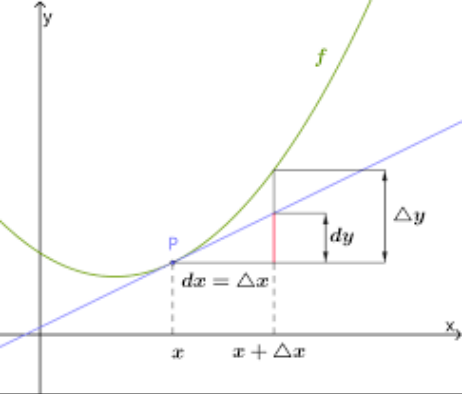
函数在 x = x 0 x=x_0 x=x0导数的定义
- 定义两点
A x 0 ( x 0 , f ( x 0 ) ) ; ( 指 定 x = x 0 处 的 极 限 ) B x = ( x , f ( x ) ) = ( x 0 + Δ x , f ( x 0 + Δ x ) ) { Δ x = x − x 0 Δ y = { f ( x ) − f ( x 0 ) f ( x 0 + Δ x ) − f ( x 0 ) x → x 0 * Δ x → 0 有 时 , 也 记 h = Δ x A_{x_0}(x_0,f(x_0));(指定x=x_0处的极限) \\ B_x=(x,f(x))=(x_0+\Delta x,f(x_0+\Delta x)) \\ \begin{cases} \Delta x=x-x_0 \\ \Delta y= \begin{cases} f(x)-f(x_0) \\ f(x_0+\Delta x)-f(x_0) \end{cases} \end{cases} \\ x\rightarrow x_0 \Longleftrightarrow \Delta x\rightarrow 0 \\有时,也记h=\Delta x Ax0(x0,f(x0));(指定x=x0处的极限)Bx=(x,f(x))=(x0+Δx,f(x0+Δx))⎩⎪⎨⎪⎧Δx=x−x0Δy={ f(x)−f(x0)f(x0+Δx)−f(x0)x→x0*Δx→0有时,也记h=Δx
lim Δ x → 0 Δ y Δ x = { lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 lim h → 0 f ( x 0 + h ) − f ( x 0 ) h \lim_{\Delta x\rightarrow 0}{\frac{\Delta y}{\Delta x}} =\begin{cases} \lim\limits_{\Delta x\rightarrow 0}{\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}} \\ \lim\limits_{x\rightarrow x_0}{\frac{f(x)-f(x_0)}{x-x_0}} \\ \lim\limits_{h\rightarrow 0}{\frac{f(x_0+h)-f(x_0)}{h} } \end{cases} Δx→0limΔxΔy=⎩⎪⎪⎪⎨⎪⎪⎪⎧Δx→0limΔxf(x0+Δx)−f(x0)x→x0limx−x0f(x)−f(x0)h→0limhf(x0+h)−f(x0)
通常,为了方便书写,经常采用第三中形式进行推导:
f ′ ( x 0 ) = lim h → 0 f ( x 0 + h ) − f ( x 0 ) h f'(x_0)=\lim\limits_{ h \rightarrow 0}{\frac{f(x_0+h)-f(x_0)}{h} } f′(x0)=h→0limhf(x0+h)−f(x0)
导函数的定义
和导数的定义类似,我们将导数定义中的 x 0 x_0 x0替换为x
f ′ ( x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x = lim h → 0 f ( x + h ) − f ( x ) h f'(x)=\lim_{\Delta x\rightarrow0}\frac{f(x+\Delta x)-f(x)}{\Delta x} =\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h} f′(x)=Δx→0limΔxf(x+Δx)−f(x)=h→0limhf(x+h)−f(x)
记
g ( h ) = f ( x + h ) − f ( x ) h g(h)=\frac{f(x+h)-f(x)}{h} g(h)=hf(x+h)−f(x)则
f ′ ( x ) = lim Δ x → 0 g ( Δ x ) = lim h → 0 g ( h ) 这 里 这 么 写 , 是 为 了 强 调 , 利 用 导 数 定 义 求 导 数 ( 导 函 数 ) 的 时 候 , 被 求 极 限 的 函 数 g ( h ) 的 自 变 量 h ( 即 f ( x ) 自 变 量 x 的 增 量 Δ x ) 与 被 求 导 数 的 f ( x ) 的 自 变 量 x 不 同 f'(x)=\lim_{\Delta x \rightarrow 0}{g(\Delta x)} =\lim_{h \rightarrow 0}{g(h)} \\这里这么写,是为了强调,利用导数定义求导数(导函数)的时候, \\被求极限的函数g(h)的自变量h(即f(x)自变量x的增量\Delta x)与被求导数的f(x)的自变量x不同 f′(x)=Δx→0limg(Δx)=h→0limg(h)这里这么写,是为了强调,利用导数定义求导数(导函数)的时候,被求极限的函数g(h)的自变量h(即f(x)自变量x的增量Δx)与被求导数的f(x)的自变量x不同显然, f ( x ) 在 x 0 处 的 导 数 f ′ ( x 0 ) 就 是 导 函 数 f ′ ( x ) 在 x = x 0 处 的 函 数 值 f(x)在x_0处的导数f'(x_0)就是导函数f'(x)在x=x_0处的函数值 f(x)在x0处的导数f′(x0)就是导函数f′(x)在x=x0处的函数值
- f ′ ( x 0 ) = f ′ ( x ) ∣ x = x 0 = d x d y f'(x_0)=f'(x)|_{x=x_0}=\frac{dx}{dy} f′(x0)=f′(x)∣x=x0=dydx
对数函数的导数推导(导数定义极限法)
f ( x ) = l o g a x f ′ ( x ) = ( l o g a x ) ′ = lim h → 0 l o g a ( x + h ) − l o g a ( x ) h = lim h → 0 l o g a ( x + h x ) h = lim h → 0 1 h l o g a ( x + h x ) = lim h → 0 l o g a ( 1 + h x ) 1 h 记 g ( h ) = l o g a ( 1 + h x ) 1 h ( l o g a x ) ′ = lim h → 0 g ( h ) ; g ( h ) 的 自 变 量 是 h ( g ( h ) 将 x 看 作 常 量 ) 该 极 限 是 1 ∞ 类 型 ; 由 第 二 重 要 极 限 的 推 广 公 式 得 到 : A = lim h → 0 h x 1 h = 1 x 所 以 对 于 u = ϕ ( h ) = ( 1 + h x ) 1 h ; u 0 = lim h → 0 u = e 1 x 又 由 复 合 函 数 的 极 限 运 算 法 则 : lim h → 0 g ( h ) = lim u → u 0 l o g a u = l o g a u 0 = l o g a e 1 x 根 据 换 底 公 式 得 到 ( l o g a x ) ′ = l o g a e 1 x = ln e 1 x ln a = 1 x 1 ln a f(x)=log_a x \\ f'(x)=(log_a x)'=\lim_{h\rightarrow 0}\frac{log_a{(x+h)}-log_a(x)}{h} =\lim_{h\rightarrow 0}\frac{log_a(\frac{x+h}{x})}{h} \\=\lim_{h\rightarrow 0}\frac{1}{h}{log_a({x+h}{x})} \\=\lim_{h\rightarrow 0}{log_a{(1+\frac{h}{x})^{\frac{1}{h}}}} \\记g(h)={log_a{(1+\frac{h}{x})^{\frac{1}{h}}}} \\(log_a x)'=\lim_{h\rightarrow 0}g(h);g(h)的自变量是h(g(h)将x看作常量) \\ 该极限是1^\infin类型; 由第二重要极限的推广公式得到:A=\lim_{h\rightarrow 0}\frac{h}{x}\frac{1}{h}=\frac{1}{x} \\所以对于u=\phi(h)=(1+\frac{h}{x})^{\frac{1}{h}}; \\ u_0=\lim_{h\rightarrow 0}{u}=e^{\frac{1}{x}} \\又由复合函数的极限运算法则: \lim_{h\rightarrow 0}g(h)=\lim_{u\rightarrow u_0}log_a{u}=log_a u_0=log_a e^\frac{1}{x} \\根据换底公式得到(log_a x)'=log_ae^{\frac{1}{x}}=\frac{\ln e^{\frac{1}{x}}}{\ln a}=\frac{1}{x}\frac{1}{\ln a} f(x)=logaxf′(x)=(logax)′=h→0limhloga(x+h)−loga(x)=h→0limhloga(xx+h)=h→0limh1loga(x+hx)=h→0limloga(1+xh)h1记g(h)=loga(1+xh)h1(logax)′=h→0limg(h);g(h)的自变量是h(g(h)将x看作常量)该极限是1∞类型;由第二重要极限的推广公式得到:A=h→0limxhh1=x1所以对于u=ϕ(h)=(1+xh)h1;u0=h→0limu=ex1又由复合函数的极限运算法则:h→0limg(h)=u→u0limlogau=logau0=logaex1根据换底公式得到(logax)′=logaex1=lnalnex1=x1lna1
导数与微分
- 微分是导数的另一种描述形式
- 导数 y ′ = d y d x y'=\frac{dy}{dx} y′=dxdy,(函数的微分dy除以自变量x的微分dx,因而导数也叫做微商)
对数函数的导函数
( l o g a x ) ′ = 1 x ln a (log_ax)'=\frac{1}{x\ln a} (logax)′=xlna1
- 对数函数的导函数可以通过第二重要极限计算得到
反函数求导法
以 a x 的 导 函 数 推 导 为 例 , 利 用 反 函 数 求 导 法 则 以a^x的导函数推导为例,利用反函数求导法则 以ax的导函数推导为例,利用反函数求导法则
直接函数
- x = x ( y ) = l o g a y x , y 取 值 范 围 : y ∈ ( 0 , + ∞ ) x ∈ ( − ∞ , + ∞ ) ( 自 变 量 y 的 ) 函 数 x 的 导 数 : x ′ ( y ) = 1 y 1 ln a x=x(y)=log_ay \\x,y取值范围: \\ y\in (0,+\infin) \\x \in (-\infin,+\infin) \\(自变量y的)函数x的导数: \\x'(y)=\frac{1}{y}\frac{1}{\ln a} \\ x=x(y)=logayx,y取值范围:y∈(0,+∞)x∈(−∞,+∞)(自变量y的)函数x的导数:x′(y)=y1lna1
反函数
- y = y ( x ) = a x * 函 数 x ( y ) 和 函 数 y ( x ) 互 为 反 函 数 y=y(x)=a^x \\ \bigstar函数x(y)和函数y(x)互为反函数 \\ y=y(x)=ax*函数x(y)和函数y(x)互为反函数
反函数的导数
- 则 : y ′ ( x ) = 1 x ′ ( y ) = 1 1 x ln a = x ln a 即 , y ′ ( x ) = ( a x ) ′ = x ln a ∴ ( a x ) ′ = x ln a 则: y'(x)=\frac{1}{x'(y)}=\frac{1}{\frac{1}{x\ln a}}=x\ln a \\即,y'(x)=(a^x)'=x\ln a \\ \therefore (a^x)'=x\ln a 则:y′(x)=x′(y)1=xlna11=xlna即,y′(x)=(ax)′=xlna∴(ax)′=xlna
对数求导法
以 求 a x 的 导 函 数 为 例 , 使 用 对 数 求 导 法 ( 伯 努 利 求 导 法 ) 以求a^x的导函数为例,使用对数求导法(伯努利求导法) 以求ax的导函数为例,使用对数求导法(伯努利求导法)
y = a x ln y = ln a x = x ln a 两 边 同 时 求 导 1 y y ′ = ln a y ′ = y ln a = a x ln a 即 , ( a x ) ′ = a x ln a y=a^x \\ \ln y=\ln a^x=x \ln a \\ 两边同时求导 \\ \frac{1}{y}y'=\ln a \\ y'=y\ln a=a^x \ln a \\ 即,(a^x)'=a^x \ln a y=axlny=lnax=xlna两边同时求导y1y′=lnay′=ylna=axlna即,(ax)′=axlna
边栏推荐
- RT thread -- FTP of LwIP (2)
- SSTI template injection explanation and real problem practice
- Pytorch基础——(1)张量(tensor)的初始化
- Blue style mall website footer code
- 自动化测试怎么规范部署?
- Pointer written test questions ~ approaching Dachang
- Mapping between QoE and KQI
- KS003基于JSP和Servlet实现的商城系统
- 3分钟带你了解微信小程序开发
- mysql从一个连续时间段的表中读取缺少数据
猜你喜欢
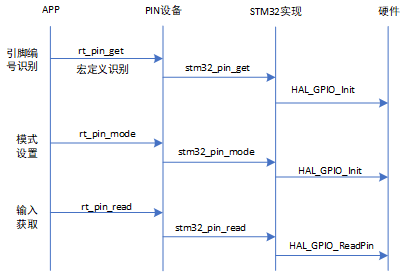
2.2 fonctionnement stm32 GPIO
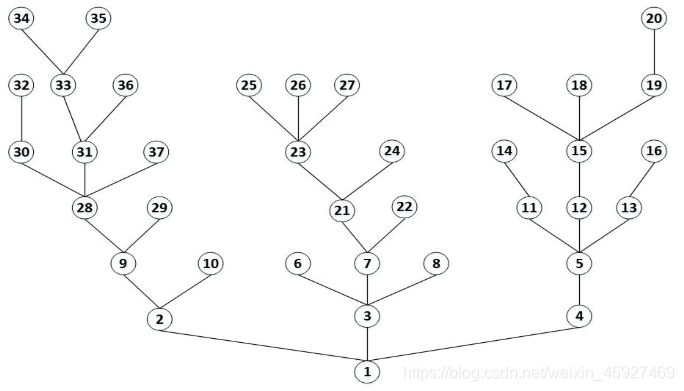
BUAA喜鹊筑巢

BUAA magpie nesting
![P7735-[noi2021] heavy and heavy edges [tree chain dissection, line segment tree]](/img/b1/dbfc42d66548476300501dd839abef.jpg)
P7735-[noi2021] heavy and heavy edges [tree chain dissection, line segment tree]
简易博客系统
Record the process of reverse task manager

JVM的手术刀式剖析——一文带你窥探JVM的秘密
![[slam] lidar camera external parameter calibration (Hong Kong University marslab) does not need a QR code calibration board](/img/07/973722bf484b374f752177dfc48ef5.png)
[slam] lidar camera external parameter calibration (Hong Kong University marslab) does not need a QR code calibration board
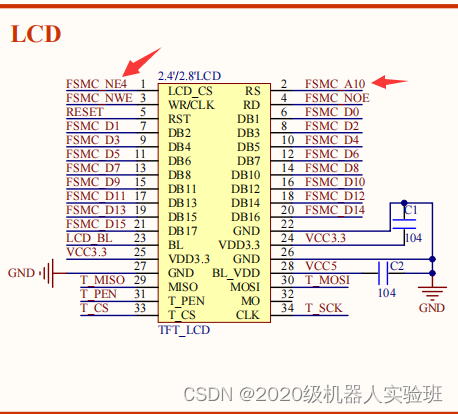
Cubemx transplantation punctual atom LCD display routine

Blue Bridge Cup - Castle formula
随机推荐
[American competition] mathematical terms
有条件地 [JsonIgnore]
2.2 STM32 GPIO操作
2.13 weekly report
2.2 STM32 GPIO操作
Image super resolution using deep revolutionary networks (srcnn) interpretation and Implementation
简述C语言中的符号和链接库
1. New project
Cf464e the classic problem [shortest path, chairman tree]
Crawler of explanation and application of agency theory
Why do you want to start pointer compression?
Cubemx 移植正点原子LCD显示例程
Schnuka: what is visual positioning system and how to position it
BUAA计算器(表达式计算-表达式树实现)
Do you know cookies, sessions, tokens?
【PSO】基于PSO粒子群优化的物料点货物运输成本最低值计算matlab仿真,包括运输费用、代理人转换费用、运输方式转化费用和时间惩罚费用
遥感图像超分辨重建综述
Hashcode and equals
Take you to wechat applet development in 3 minutes
The solution of permission denied (750 permissions should be used with caution)