当前位置:网站首页>Hand tear - sort
Hand tear - sort
2022-07-02 03:53:00 【Programming share】
Insertion sort
The premise of inserting sorting is When not inserted, the sequence is ordered .
If it is sorted from small to large , The number of inserts is key, Find less than or equal to... From right to left key Value , If it is not satisfied, then move back one bit to cover , Insert until it is satisfied or found .
Repeat the above .
void InsertSort(int* a, int n)
{
int i = 0;
for (i = 0; i < n-1; i++)
{
int end=i;
int key = a[end + 1];
while (end>=0)
{
if (a[end] <= key)
break;
else
a[end + 1] = a[end];
end--;
}
a[end + 1] = key;
}
}
Time complexity O(n*n)
This sort is suitable for the case of near order , In this case Time complexity is close to O(n)
Shell Sort
There is an evolution of insertion sorting
Hill sorting has two steps :
1. Pre sort ( Be as orderly as possible )
2. Insertion sort
example :
Pre sort : Divide the group of numbers to be sorted into gap Group , Insert and sort each group
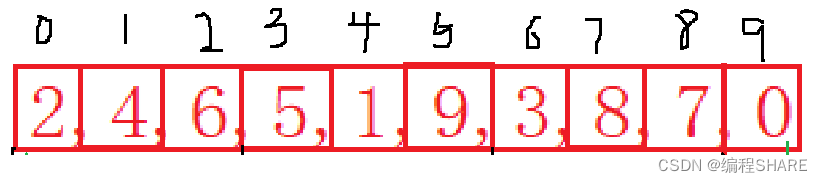
Put this 10 Group number division 3 Group :
The first 1 Group :2,5,3,0
The first 2 Group :4,1,8
The first 3 Group :6,9,7
The sequence after pre arrangement 
Finally, insert and sort all , You can get an ordered sequence .
The code of the above example :
void ShellSort(int* a, int n)
{
int gap = 3;
for (int i = 0; i < n-gap; i++)
{
int end=i;
int key = a[end + gap];
while (end >= 0)
{
if (a[end] <= key)
break;
else
a[end + gap] = a[end];
end -= gap;
}
a[end + gap] = key;
}
InsertSort(a, n);
}
Hill sort dynamic graph 
void ShellSort(int* a, int n)
{
int gap = n;
while (gap>1)
{
gap = gap / 2;
for (int i = 0; i < n-gap; i++)
{
int end = i;
int key = a[end + gap];
while (end >= 0)
{
if (a[end] <= key)
break;
else
a[end + gap] = a[end];
end -= gap;
}
a[end + gap] = key;
}
}
}
Selection sort

It's easy to sort by selection , Each time, choose the smallest one in front , Choose the biggest one and put it in the back .
void SelectSort(int* a, int n)
{
int min, max;
int begin = 0, end = n - 1;
while (begin < end)
{
min = max = begin;
for (int i = begin; i <= end; i++)
{
if (a[min] > a[i])
min = i;
if (a[max] < a[i])
max = i;
}
swap(&a[min], &a[begin]);
// Be careful
if (begin == max)
max = min;
swap(&a[max], &a[end]);
begin++;
end--;
}
}
Time complexity O(N)
Heap sort

void AdjustDwon(int* a, int n, int root)
{
int father = root;
int child = 2 * father + 1;
while (child <n)
{
if (child<n - 1 && a[child]<a[child + 1])
child++;
if (a[father] < a[child])
{
swap(&a[father], &a[child]);
father = child;
child = 2 * father + 1;
}
else
return;
}
}
void HeapSort(int* a, int n)
{
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDwon(a, n, i);
}
for (i = n - 1; i > 0; i--)
{
swap(&a[0], &a[i]);
AdjustDwon(a, i-1, 0);
}
}
Bubble sort

void BubbleSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
for (int i = begin; i < n-1; i++)
{
for (int j = begin; j < end; j++)
{
if (a[j+1] < a[j])
swap(&a[j], &a[j+1]);
}
end--;
}
}
Quick sort

The basic idea of quick sorting is : Choose a base value , Generally, the leftmost one is selected as the base value , Then start traversing from the right , Suppose it is in the order from small to large , Then look for the small one on the right , After finding the small one , Look for the biggest one from the left , After finding them, exchange them . Then continue to repeat the above process , Stop until the left is greater than or equal to the right , Then exchange with the cardinality .
This is a round
int PartSort1(int* a, int left, int right)
{
int keyi = left;
while (left < right)
{
while (left < right && a[keyi] <= a[right])
right--;
while (left < right && a[left] <= a[keyi])
left++;
swap(&a[left], &a[right]);
}
swap(&a[keyi], &a[right]);
keyi = left;
return keyi;
}
Pit method : Take the cardinality as the pit position , Start from the right to find small ( Smaller than base ) Of , Fill in the pit after finding it , This position becomes a pit , Then start from the left to find the big , Then fill in the pit , Until you find it ( The left is greater than or equal to the right ), Fill the base number in the pit .
int PartSort2(int* a, int left, int right)
{
int keyi= left;
int temp = a[left];
while (left < right)
{
while (left<right&&a[right] >= temp)
{
right--;
}
a[keyi] = a[right];
keyi = right;
while (left < right && a[left] <= temp)
{
left++;
}
a[keyi] = a[left];
keyi = left;
}
a[keyi] = temp;
return keyi;
}
Front and back pointer method :
The front pointer starts from the position before the cardinality , The post pointer starts at the base position . The front pointer looks small , When you find a little , Add one to the back pointer , Then the values pointed by the front and back pointers are exchanged , Then the front pointer continues to look small , Until the search is complete .
int PartSort3(int* a, int left, int right)
{
int keyi = left;
int front = keyi + 1;
int back = keyi;
while (front <= right)
{
if (a[front] <= a[keyi])
{
back++;
swap(&a[front], &a[back]);
}
front++;
}
swap(&a[back], &a[keyi]);
keyi = back;
return keyi;
}
The above description is a round of sorting , After each round , Can determine the position of the cardinality after sorting , The left side of the cardinality is smaller , On the right is bigger than it , Continue sorting on the left , The right side continues to sort . Stop sorting when there is one left to sort .
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = left;
//keyi = PartSort1(a, left, right);
//keyi = PartSort2(a, left, right);
keyi = PartSort3(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}
The above sort is not enough , Because his worst time complexity is O(N*N), The best cardinality we take is the middle value of the group with ordinal numbers , But this value is not easy to find in disorder , Now we use 3 Take the middle method , Put the marginal value , The rightmost value , And the middle value ,3 Compare with , The next largest is the base . In order to ensure the above method , We exchange the cardinality with the leftmost number .
int ThreeIn(int* a, int left, int right)
{
int middle = left + (right - left) / 2;
if (a[middle] < a[left])
{
if (a[left] < a[right])
return left;
else if (a[middle] < a[right])
return right;
else
return middle;
}
else
{
if (a[middle] < a[right])
return middle;
else if (a[left] < a[right])
return right;
else
return left;
}
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = left;
int x = ThreeIn(a, left, right);
swap(&a[keyi], &a[x]);
//keyi = PartSort1(a, left, right);
//keyi = PartSort2(a, left, right);
keyi = PartSort3(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}
Time complexity O(N*logN)
Base on the leftmost , Why start on the right ?
stay L And R There is nothing to discuss in the exchange process , The most important thing is the exchange with the cardinality when meeting :
1.R meet L, here L Is the smallest or cardinal , After the exchange , Left small right big .
2.L meet R:
(1)L And R No exchange
R The position is small ,R On the right are big , On the left are small , It can be exchanged with the base value .
(2)L And R In exchange for
After the exchange R Will continue to move to small places , And then (1) equally .
Let's talk about choosing the left as the base value , Or discuss the encounter
1.L meet R
(1) Met without exchange , It is impossible to judge the size of the base value when meeting .
(2)L And R Meet again after exchange , At this time, the meeting is big , Cannot exchange with base value .
2.R meet L
R meet L explain R And L Exchanged , At this time, the base value is small , You can exchange .
in summary : Starting from the left does not completely guarantee that the place where you meet is small .
Non recursive quick sort
1. Implement with stack
Store the upper and lower bounds of a group of numbers with a stack , If you choose the cardinality from the left , According to the nature of the stack , Let's store the left boundary first , Then save the right boundary . Every sort takes it out of the stack 2 Data . When storing boundaries to the stack, you should directly check whether there are elements in the main boundary .
void QuickSortNonR1(int* a, int left, int right)
{
Stack p;
InitStack(&p);
StackPush(&p, left);
StackPush(&p, right);
while (!StackEmpty(&p))
{
right = StackTop(&p);
StackPop(&p);
left = StackTop(&p);
StackPop(&p);
int keyi = PartSort3(a, left, right);
if (keyi + 1 < right)
{
StackPush(&p, keyi+1);
StackPush(&p, right);
}
if (keyi - 1 > left)
{
StackPush(&p, left);
StackPush(&p, keyi-1);
}
}
StackDestroy(&p);
}
2. Implement... With queues
According to the nature of the queue , First save the right boundary , Then save the left boundary . The following process is similar to stack
void QuickSortNonR2(int* a, int left, int right)
{
Queue p;
QueueInit(&p);
QueuePush(&p, right);
QueuePush(&p, left);
while (!QueueEmpty(&p))
{
right = QueueFront(&p);
QueuePop(&p);
left= QueueFront(&p);
QueuePop(&p);
int keyi = PartSort3(a, left, right);
if (keyi - 1 > left)
{
QueuePush(&p, keyi - 1);
QueuePush(&p, left);
}
if (keyi + 1 < right)
{
QueuePush(&p, right);
QueuePush(&p, keyi + 1);
}
}
QueueDestroy(&p);
}
Merge sort
边栏推荐
- "No war on the Western Front" we just began to love life, but we had to shoot at everything
- go 语言命名规范
- Blue Bridge Cup SCM digital tube skills
- [yolo3d]: real time detection of end-to-end 3D point cloud input
- [Li Kou brush questions] 15 Sum of three numbers (double pointer); 17. Letter combination of phone number (recursive backtracking)
- 一文彻底理解评分卡开发中——Y的确定(Vintage分析、滚动率分析等)
- SQL:常用的 SQL 命令
- Vite: configure IP access
- 高性能 低功耗Cortex-A53核心板 | i.MX8M Mini
- Homework in Chapter 3 of slam course of dark blue vision -- derivative application of T6 common functions
猜你喜欢
蓝桥杯单片机省赛第十届
Fourier series

u本位合约爆仓清算解决方案建议
![[Li Kou brush questions] 15 Sum of three numbers (double pointer); 17. Letter combination of phone number (recursive backtracking)](/img/5e/81e613370c808c63665c14298f9a39.png)
[Li Kou brush questions] 15 Sum of three numbers (double pointer); 17. Letter combination of phone number (recursive backtracking)
树莓派GPIO引脚控制红绿灯与轰鸣器
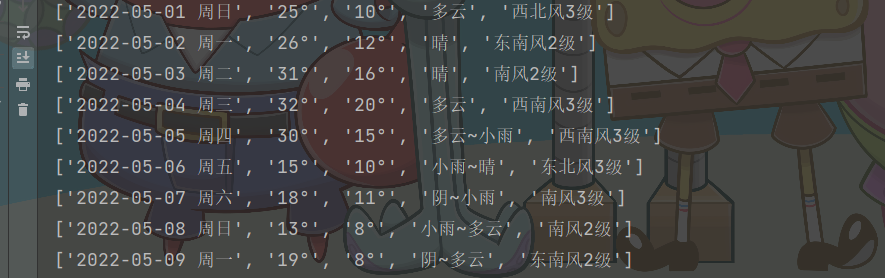
近段时间天气暴热,所以采集北上广深去年天气数据,制作可视化图看下
![[ibdfe] matlab simulation of frequency domain equalization based on ibdfe](/img/a1/441f400668e736b70cb36443f2267a.png)
[ibdfe] matlab simulation of frequency domain equalization based on ibdfe

A thorough understanding of the development of scorecards - the determination of Y (Vintage analysis, rolling rate analysis, etc.)

First acquaintance with string+ simple usage (II)
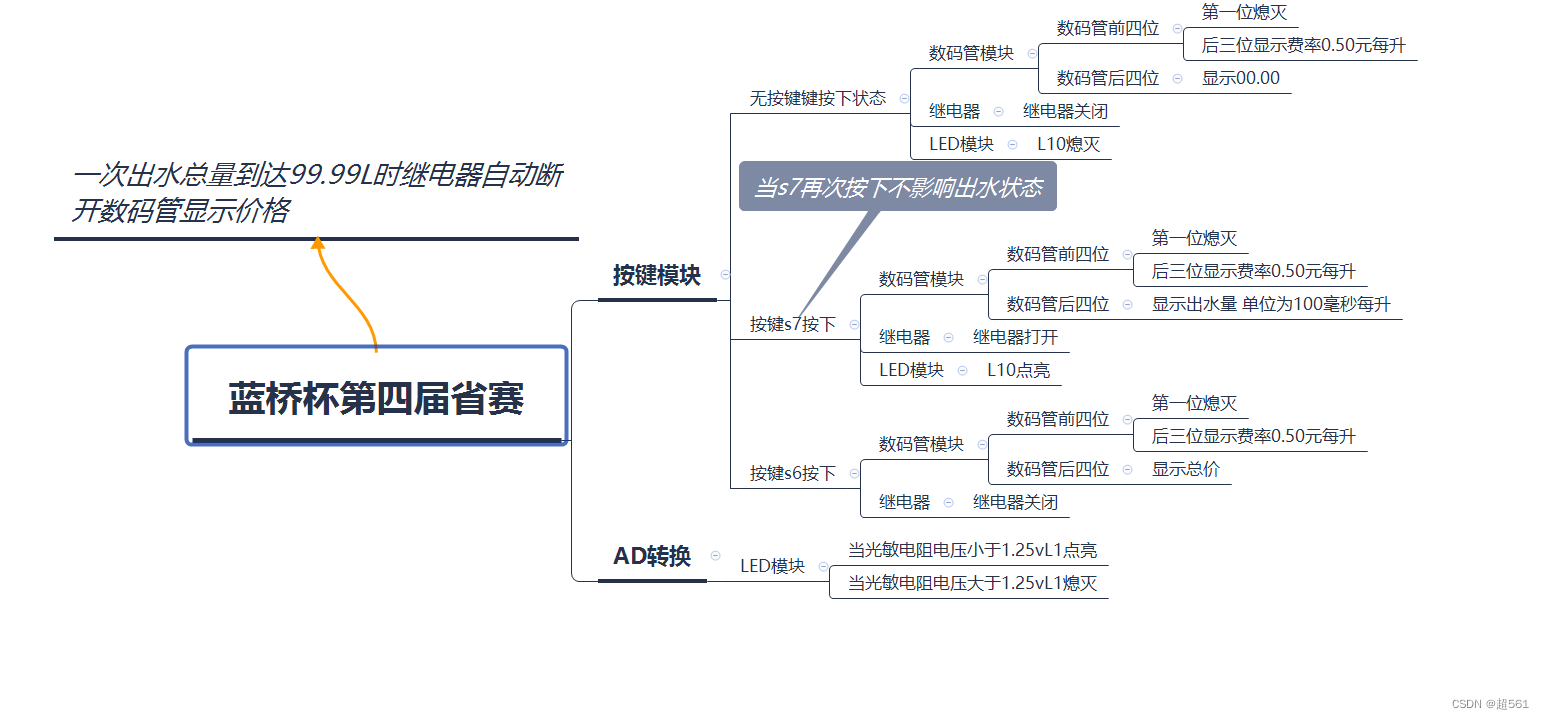
The fourth provincial competition of Bluebridge cup single chip microcomputer
随机推荐
Jetpack's livedata extension mediatorlivedata
Flutter中深入了解MaterialApp,常用属性解析
The 9th Blue Bridge Cup single chip microcomputer provincial competition
The 8th Blue Bridge Cup single chip microcomputer provincial competition
Introduction to Robotics II. Forward kinematics, MDH method
Account management of MySQL
【直播回顾】战码先锋首期8节直播完美落幕,下期敬请期待!
The first game of the 11th provincial single chip microcomputer competition of the Blue Bridge Cup
Hands on deep learning (II) -- multi layer perceptron
The 7th Blue Bridge Cup single chip microcomputer provincial competition
Pandora IOT development board learning (HAL Library) - Experiment 2 buzzer experiment (learning notes)
Imageai installation
[wireless image transmission] FPGA based simple wireless image transmission system Verilog development, matlab assisted verification
Pandora IOT development board learning (RT thread) - Experiment 1 LED flashing experiment (learning notes)
go 语言命名规范
《动手学深度学习》(二)-- 多层感知机
Basic operations of MySQL database (based on tables)
Blue Bridge Cup SCM digital tube skills
【DesignMode】建造者模式(Builder model)
Influence of air resistance on the trajectory of table tennis