求组合数 AcWing 889. 满足条件的01序列

原题链接

AcWing 889. 满足条件的01序列

算法标签

组合数学 组合计数 卡特兰数 逆元 快速幂 费马小定理

思路

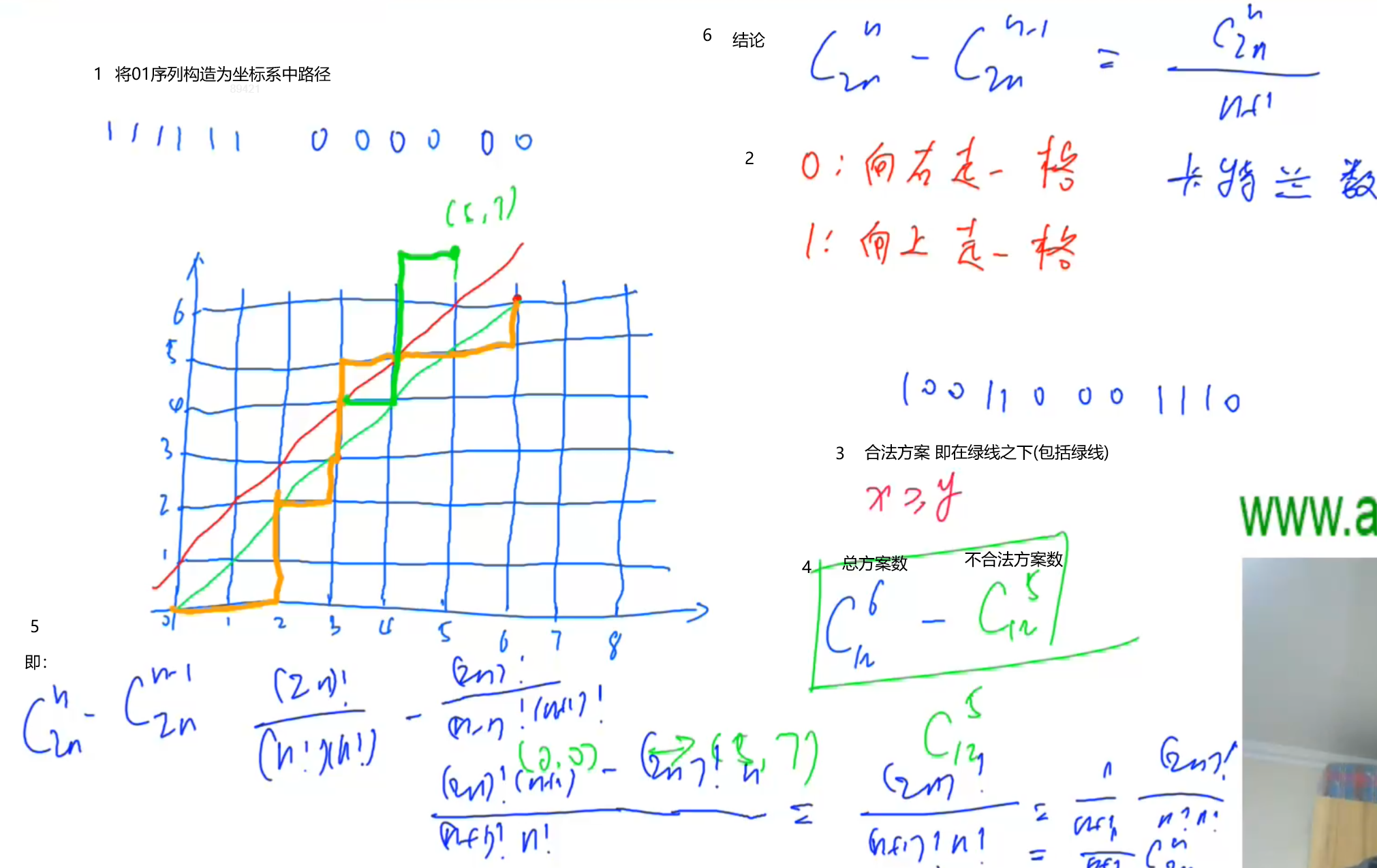
代码

#include<bits/stdc++.h>
#define int long long
#define abs fabs
#define rep(i, a, b) for(int i=a;i<b;++i)
#define Rep(i, a, b) for(int i=a;i>=b;--i)
using namespace std;
const int N = 100005, mod = 1e9+7;
int pr[N], st[N], s[N], cnt;
inline int read(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}
void put(int x) {
    if(x<0) putchar('-'),x=-x;
    if(x>=10) put(x/10);
    putchar(x%10^48);
}
int qmi(int a, int b, int p){
    int ans=1;
    while(b){
        if(b&1){
            ans=ans*a%p;
        }
        a=a*a%p;
        b>>=1;
    }
    return ans;
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n=read();
    int res=1;
    // Cn 2n 
    Rep(i, 2*n, n+1){
        res=res*i%mod;
    }
    // / n + 1 % p 需求逆元
    rep(i, 1, n+2){
        res=res*qmi(i, mod-2, mod)%mod;
    }
    printf("%lld\n", res);
}

原创不易
转载请标明出处
如果对你有所帮助 别忘啦点赞支持哈