当前位置:网站首页>Model-Free Control
Model-Free Control
2022-07-07 00:27:00 【Evergreen AAS】
The last one is a summary Model-Free Predict Problems and methods , The content of this paper Model-Free Control Method , namely “Optimise the value function of an unknown MDP”.
Explain here ,Model-Free Predict/Control Not just for Model-Free The situation of , It also applies to MDP Known problem :
- MDP model is unknown, but experience can be sampled.
- MDP model is known, but is too big to use, except by samples.
In the official introduction Model-Free Control Before method , Let's introduce On-policy Learning And Off-policy Learning.
On-policy Learning vs. Off-policy Learning
On-policy Learning:
- “Learn on the job”
- Learn about policy π from experience sampled from π( That is, the sampling strategy is consistent with the learning strategy )
Off-policy Learning:
- “Look over someone’s shoulder”
- Learn about policy π from experience sampled from μ( That is, the sampling strategy is inconsistent with the learning strategy )
On-Policy Monte-Carlo Learning
Generalized Policy Iteration
Concrete Control Method , stay 《 Dynamic programming 》 In the article, we mentioned Model-based Generalized strategy iteration under GPI frame , That's in Model-Free Is it also applicable in case ? The picture below shows Model-based Generalized strategy iteration under GPI frame , There are mainly two parts : Strategy evaluation and based on Greedy Strategy improvement of strategy .
Model-Free Strategy assessment
stay 《Model-Free Predict》 We introduced two kinds of Model-Free Strategy evaluation method :MC and TD. Let's talk about using MC Cases of Model-Free Strategy assessment . Pictured above GPI As shown in the frame :
- be based on V(s) The improvement of greedy strategy needs MDP It is known that :
\pi'(s) = \arg\max_{a\in A}\Bigl(R_{s}^{a}+P_{ss'}^{a}V(s')\Bigr)
- be based on Q(s,a) There is no need to MDP It is known that , namely Model-Free:
\pi'(s) = \arg\max_{a\in A}Q(s, a)
therefore Model-Free I need to be right Q(s,a) Strategy assessment , Whole GPI Strategy iteration should also be based on Q(s,a)
Model-Free Strategy improvement
Determine the object of strategy evaluation , The next thing to consider is how to evaluate the results based on strategies Q(s,a) Carry out strategy improvement . because Model-Free Our strategy evaluation is based on experience samples( That is, evaluated q(s,a) There is bias), So we don't use pure greedy Strategy , Prevent the deviation of strategy evaluation from leading the whole strategy iteration to local optimization , Instead, it uses explore Functional ϵ-greedy Algorithm :
\pi(a|s) = \begin{cases} &\frac{\epsilon}{m} + 1 - \epsilon, &\text{if } a^*=\arg\max_{a\in A}Q(s, a)\\ &\frac{\epsilon}{m}, &\text{otherwise} \end{cases}
therefore , We're sure Model-Free Under the Monto-Carlo Control:
GLIE
First, post it directly David The courseware of ,GLIE Introduce the following :
about ϵ-greedy In terms of algorithm , If ϵ As the number of iterations gradually decreases to 0, that ϵ-greedy yes GLIE, namely :
\epsilon_{k} = \frac{1}{k}
GLIE Monto-Carlo Control
- about episode Each state in S~t~ And the action A~t~
N(S_t, A_t) ← N(S_t, A_t) + 1 \\ Q(S_t, A_t) ← Q(S_t, A_t) + \frac{1}{N(S_t, A_t)}(G_t - Q(S_t, A_t))
- Based on the new action value function promotion strategy :
\epsilon ← \frac{1}{k}\\ \pi ← \epsilon\text{-greedy}(Q)
Theorem :GLIE Monto-Carlo Control Converge to the optimal action value function , namely :
Q(s, a) → q_*(s, a)
On-Policy Temporal-Difference Learning
Sarsa
We have concluded before TD relative MC The advantages of :
- Low variance
- Online
- Incomplete sequence
Then a natural idea is to use TD Instead of MC:
- Use TD To calculate Q(S,A)
- Still use ϵ-greedy Strategy improvement
- every last step updated
Through the above changes On-Policy The Monte Carlo method of became famous Sarsa.
- Update the action value function
- Control
Sarsa The pseudo-code of the algorithm is as follows :
Sarsa(λ)
n-step Sarsa returns It can be expressed as follows :n=1 when :q_{t}^{(1)} = R_{t+1} + \gamma Q(S_{t+1})n=2 when :q_{t}^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma^2 Q(S_{t+2})…n=∞ when :q_{t}^{\infty} = R_{t+1} + \gamma R_{t+2} + … + \gamma^{T-1} R_T) therefore ,n-step return q_{t}^{(n)} = R_{t+1} + \gamma R_{t+2} + … + \gamma^{n}Q(S_{t+n})
n-step Sarse Update formula :
Q(S_t,A_t) ← Q(S_t,A_t) + \alpha (q_t^{(n)} - Q(S_t,A_t))
Concrete Sarsa(λ) The algorithm pseudo code is as follows :
among E(s,a) For qualification trace .
The following figure for Sarsa(λ) be used for Gridworld Schematic diagram of the example :
Off-Policy Learning
Off-Policy Learning The characteristic of is to evaluate the target strategy π(a|s) To calculate v~π~(s) perhaps q~π~(s,a) But follow behavioral strategies {S~1~,A~1~,R~2~,…,S~T~}∼μ(a|s)
Off-Policy Learning What's the point ?
- Learn from observing humans or other agents
- Re-use experience generated from old policies π~1~,π~2~,…,π~t−1~
- Learn about optimal policy while following exploratory policy
- Learn about multiple policies while following one policy
Importance sampling
The purpose of importance sampling is :Estimate the expectation of a different distribution.
\begin{align} E_{X\sim P}[f(X)] &= \sum P(X)f(X)\\ &= \sum Q(X)\frac{P(X)}{Q(X)}f(X)\\ &= E_{X\sim Q}[\frac{P(X)}{Q(X)}f(X)] \end{align}
Off-Policy MC Importance sampling
Use policy π Produced return To assess the μ :
G_t^{\pi/\mu} = \frac{\pi(A_t|S_t)}{\mu(A_t|S_t)} \frac{\pi(A_{t+1}|S_{t+1})}{\mu(A_{t+1}|S_{t+1})}...\frac{\pi(A_T|S_T)}{\mu(A_T|S_T)}G_t
Towards the right return Direction to update value :
V(S_t) ← V(S_t) + \alpha\Bigl(\textcolor{Red}{G_t^{\pi/\mu}}-V(S_t)\Bigr)
Two things to note :
- Cannot use if μ is zero when π is non-zero
- Importance sampling will significantly increase variance
Off-Policy TD Importance sampling
TD It's a one-step , So use strategy π Produced TD targets To assess the μ :
V(S_t) ← V(S_t) + \alpha\Bigl(\frac{\pi(A_t|S_t)}{\mu(A_t|S_t)}(R_{t+1}+\gamma V(S_{t+1}))-V(S_t)\Bigr)
- Variance ratio MC The importance of version sampling is much lower
Q-Learning
Previously, we introduced the value function V(s) Conduct off-policy Study , Now let's discuss how to evaluate the action value function Q(s,a) Conduct off-policy Study :
- No importance sampling is required
- Use behavioral strategies to choose the next action :A_{t+1}\sim\mu(·|S_t)
- But there is still another follow-up action to consider :A’\sim\pi(·|S_t)
- Update towards the value of another subsequent action Q(S_t, A_t)
Q(S_t, A_t) ← Q(S_t, A_t) + \alpha\Bigl(R_{t+1}+\gamma Q(S_{t+1}, A')-Q(S_t, A_t)\Bigr)
After discussing the learning of action value function , Let's see how to pass Q-Learning Conduct Control:
- Both behavior strategy and goal strategy are improved
- Target strategy π With greedy Ways to improve :
\pi(S_t) = \arg\max_{a'}Q(S_{t+1}, a')
- Behavioral strategies μ With ϵ-greedy Ways to improve
- Q-Learning target:
\begin{align} &R_{t+1}+\gamma Q(S_{t+1}, A')\\ =&R_{t+1}+\gamma Q\Bigl(S_{t+1}, \arg\max_{a'}Q(S_{t+1}, a')\Bigr)\\ =&R_{t+1}+\max_{a'}\gamma Q(S_{t+1}, a') \end{align}
Q-Learning Of backup tree As shown below :
About Q-Learning Conclusion :
Q-learning control converges to the optimal action-value function, Q(s,a)→q~∗~(s,a)
Q-Learning The specific pseudo code of the algorithm is as follows :
contrast Sarsa And Q-Learning Two of the most important differences can be found :
- TD target Different formulas
- Q-Learning The next action in is selected from the behavior strategy , Not the target strategy
DP vs. TD
The differences between the two are shown in the table below :
边栏推荐
- 从外企离开,我才知道什么叫尊重跟合规…
- 【CVPR 2022】目标检测SOTA:DINO: DETR with Improved DeNoising Anchor Boxes for End-to-End Object Detection
- Are you ready to automate continuous deployment in ci/cd?
- Oracle EMCC 13.5 environment in docker every minute
- 使用源码编译来安装PostgreSQL13.3数据库
- Huawei mate8 battery price_ Huawei mate8 charges very slowly after replacing the battery
- 如何判断一个数组中的元素包含一个对象的所有属性值
- TypeScript中使用类型别名
- Use package FY in Oracle_ Recover_ Data. PCK to recover the table of truncate misoperation
- pinia 模块划分
猜你喜欢
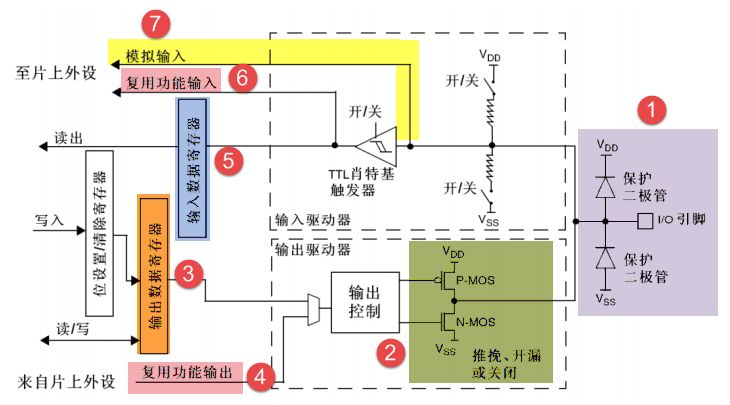
Introduction to GPIO
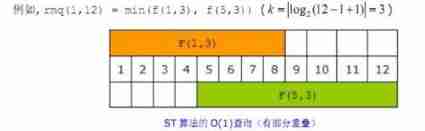
St table

Introduction au GPIO
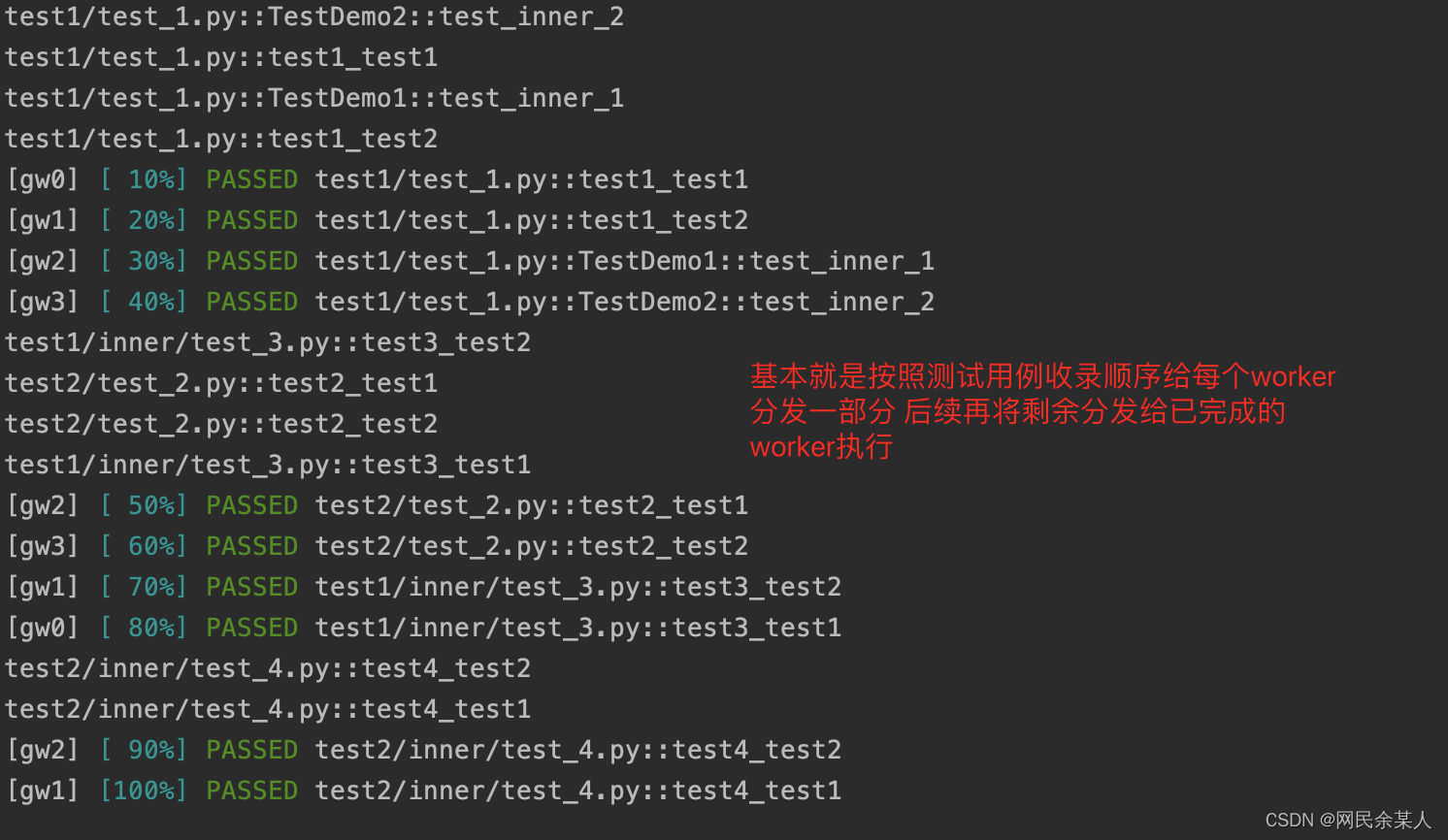
pytest多进程/多线程执行测试用例
How engineers treat open source -- the heartfelt words of an old engineer

GPIO簡介
![[2022 the finest in the whole network] how to test the interface test generally? Process and steps of interface test](/img/8d/b59cf466031f36eb50d4d06aa5fbe4.jpg)
[2022 the finest in the whole network] how to test the interface test generally? Process and steps of interface test
What is AVL tree?

Understand the misunderstanding of programmers: Chinese programmers in the eyes of Western programmers

GPIO简介
随机推荐
Designed for decision tree, the National University of Singapore and Tsinghua University jointly proposed a fast and safe federal learning system
Clipboard management tool paste Chinese version
uniapp中redirectTo和navigateTo的区别
Testers, how to prepare test data
使用yum来安装PostgreSQL13.3数据库
基于GO语言实现的X.509证书
@TableId can‘t more than one in Class: “com.example.CloseContactSearcher.entity.Activity“.
Leecode brush questions record sword finger offer 11 Rotate the minimum number of the array
Understand the misunderstanding of programmers: Chinese programmers in the eyes of Western programmers
MIT 6.824 - Raft学生指南
Rails 4 asset pipeline vendor asset images are not precompiled
2022年PMP项目管理考试敏捷知识点(9)
rancher集成ldap,实现统一账号登录
vector的使用方法_vector指针如何使用
【精品】pinia 基于插件pinia-plugin-persist的 持久化
Data operation platform - data collection [easy to understand]
Leecode brushes questions and records interview questions 01.02 Determine whether it is character rearrangement for each other
Geo data mining (III) enrichment analysis of go and KEGG using David database
Leecode brush question record sword finger offer 56 - ii Number of occurrences of numbers in the array II
SQL的一种写法,匹配就更新,否则就是插入