当前位置:网站首页>[JS] - [dynamic planning] - Notes
[JS] - [dynamic planning] - Notes
2022-07-04 23:17:00 【Interesting learning】
【js】-【 Dynamic programming 】- note
1 How to find coins gracefully
Give coins of different denominations coins And a total amount amount. Write a function to calculate the amount needed to make up the total amount least Number of coins . If no combination of coins can make up the total amount , return -1.
Example 1:
Input : coins = [1, 2, 5], amount = 11
Output : 3
explain : 11 = 5 + 5 + 1
Example 2:
Input : coins = [2], amount = 3
Output : -1
const coinChange = function(coins, amount) {
# It is used to save the minimum number of coins corresponding to each target total
const f = []
f[0] = 0
# Traverse [1, amount] The total amount of coins in this range
for(let i=1;i<=amount;i++) {
# It's the minimum , We assume infinity
f[i] = Infinity
// Loop through the denomination of each available coin
for(let j=0;j<coins.length;j++) {
# If the denomination is less than the target total , Then the problem holds
if(i-coins[j]>=0) {
// State transition equation
f[i] = Math.min(f[i],f[i-coins[j]]+1)
}
}
}
// If the solution corresponding to the target sum is infinite , It means that there is no eligible total number of coins to update it , There is no solution to this problem , return -1
if(f[amount]===Infinity) {
return -1
}
// If there is a solution , Return the content of the solution directly
return f[amount]
};
2 0-1 knapsack problem
Yes n Item , The volume of the object is called w Save the array of , The value of an item is called value Save the array of ; The volume of each article is w[i] To express , The value of each item is value[i] To express . There is now a capacity of c The backpack , Ask how you choose items to put into your backpack , In order to maximize the total value of the items in the backpack ?
Be careful : There are only 1 Pieces of
# Participation is the number of items and the upper limit of the backpack , And an array of weights and values of items
function knapsack(n, c, w, value) {
// dp Is a dynamic planning state saving array
const dp = (new Array(c+1)).fill(0)
# res It is used to record the maximum value in all combination schemes
let res = -Infinity
for(let i=1;i<=n;i++) {
for(let v=c;v>=w[i];v--) {
// Write the equation of state transition
dp[v] = Math.max(dp[v], dp[v-w[i]] + value[i])
// Update the maximum value immediately
if(dp[v] > res) {
res = dp[v]
}
}
}
return res
}
3 Longest ascending subsequence model
Title Description : Given an unordered array of integers , Find the length of the longest ascending subsequence .
Example :
Input : [10,9,2,5,3,7,101,18]
Output : 4
explain : The longest ascending subsequence is [2,3,7,101], Its length is 4.
var lengthOfLIS = function(nums) {
if(!nums.length) return 0;
# Initialize the status value of each index bit in the array
const dp= new Array(nums.length).fill(1);
let res =1;
for(let i=1;i<nums.length;i++){
for(let j=0;j<i;j++){
# If you encounter a value smaller than the current element , It means that an ascending subsequence that can be extended , Therefore, update the status corresponding to the index bit of the current element
if(nums[j]<nums[i]) dp[i]=Math.max(dp[i],dp[j]+1);
}
res= Math.max(dp[i],res);
}
return res;
};
边栏推荐
- Async await used in map
- [binary tree] the maximum difference between a node and its ancestor
- Redis入门完整教程:集合详解
- QT personal learning summary
- 实战模拟│JWT 登录认证
- P2181 diagonal and p1030 [noip2001 popularization group] arrange in order
- Redis getting started complete tutorial: hash description
- P2181 对角线和P1030 [NOIP2001 普及组] 求先序排列
- 数据库基础知识
- SPH中的粒子初始排列问题(两张图解决)
猜你喜欢
![[sword finger offer] questions 1-5](/img/54/b70d5290978e842939db99645c6ada.png)
[sword finger offer] questions 1-5
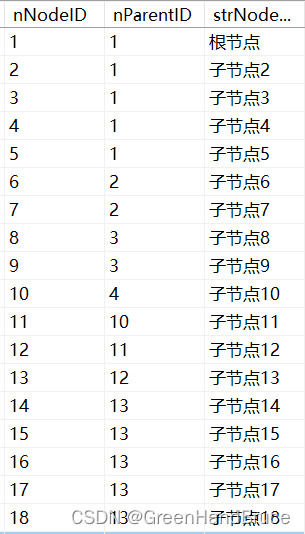
QT drawing network topology diagram (connecting database, recursive function, infinite drawing, dragging nodes)

Network namespace
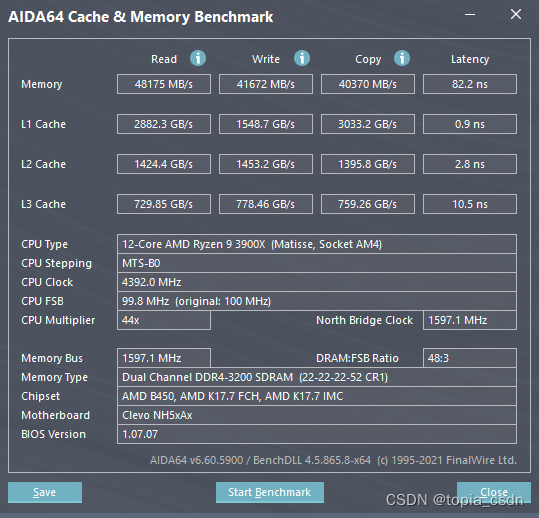
Blue sky nh55 series notebook memory reading and writing speed is extremely slow, solution process record
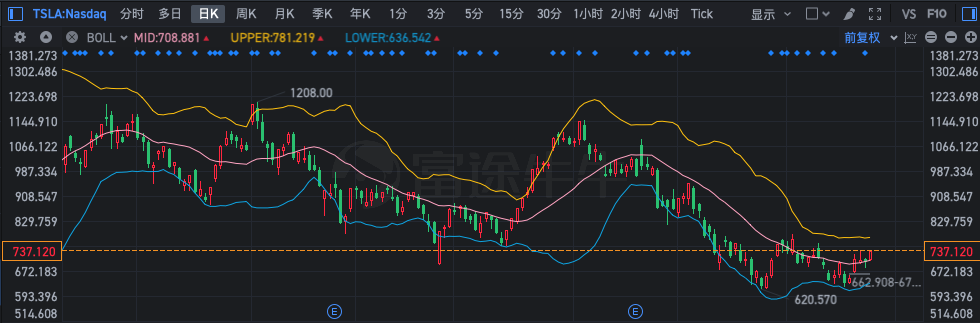
One of the commonly used technical indicators, reading boll Bollinger line indicators
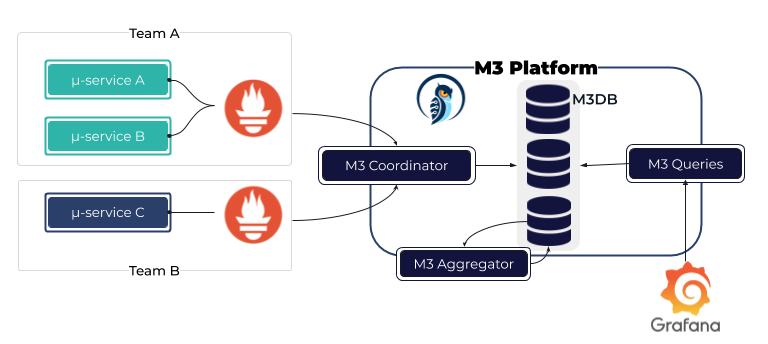
Observable time series data downsampling practice in Prometheus
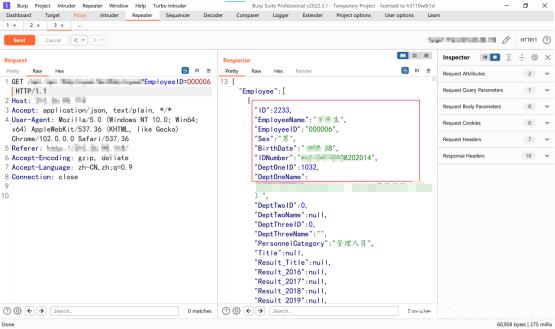
A mining of edu certificate station

MariaDB的Galera集群-双主双活安装设置
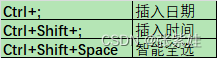
Excel 快捷键-随时补充

【剑指Offer】6-10题
随机推荐
QT addition calculator (simple case)
Excel shortcut keys - always add
Pagoda 7.9.2 pagoda control panel bypasses mobile phone binding authentication bypasses official authentication
ICML 2022 || 3DLinker: 用于分子链接设计的E(3)等变变分自编码器
【二叉树】节点与其祖先之间的最大差值
SPH中的粒子初始排列问题(两张图解决)
qt绘制网络拓补图(连接数据库,递归函数,无限绘制,可拖动节点)
C语言快速解决反转链表
heatmap. JS picture hotspot heat map plug-in
Qt个人学习总结
Redis getting started complete tutorial: publish and subscribe
The caching feature of docker image and dockerfile
Object detection based on OpenCV haarcascades
ECCV 2022 | 腾讯优图提出DisCo:拯救小模型在自监督学习中的效果
【爬虫】数据提取之JSONpath
Qt加法计算器(简单案例)
Explanation of bitwise operators
Redis入门完整教程:API的理解和使用
机器学习在房屋价格预测上的应用
EditPlus--用法--快捷键/配置/背景色/字体大小