当前位置:网站首页>深度学习(四)分析问题与调参 理论部分
深度学习(四)分析问题与调参 理论部分
2022-08-05 11:08:00 【Ali forever】
前言
调参是深度学习里面十分重要的一个事情,不断地调整参数调整模型结构能够使模型的准确度大大提升,下面就探究如何合理分析问题
一、分数低的一般原因
我们对于训练出来的模型评分较低时,我们应该按照一个比较清晰的逻辑去分析问题,而不是随便地修改,我们要严格按照以下的顺序进行分析问题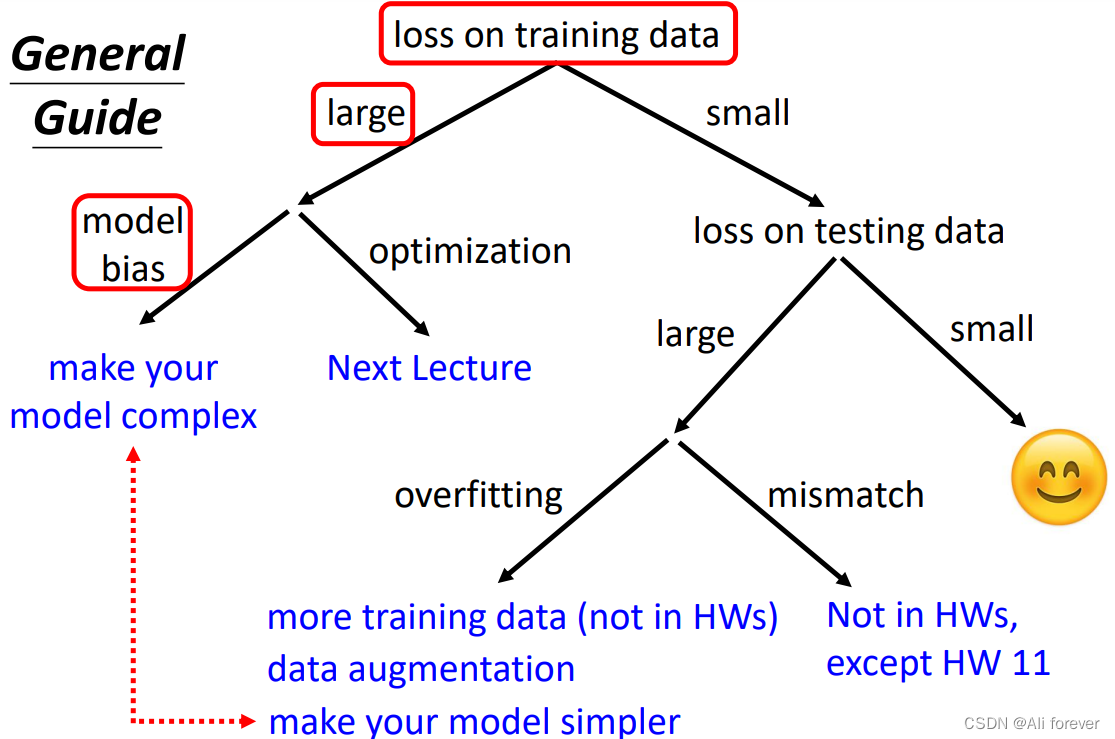
1.训练集损失函数过大
此时我们一般会考虑两种情况:model bias,optimization问题
1.model bias
所谓model bias问题就是指我们所设置的模型过于简单,无论怎么进行梯度下降等最优化手段都无法提高准确率。
解决方法为:
重新设置一个更复杂的模型,比如增加特征数量,用更深层的神经网络。
像第一节内容的改变模型,就是利用了这种方法。
2.optimization
这种情况是因为最优化的时间太短,没有达到收敛就结束了,所以最后无法得到一个很好的训练loss。
3.如何分辨model bias和optimization?
optimization的一个最显著的特点是:在训练集中训练的层级更大,反而比低层级的训练方式得到的Loss值更加大。
解决方法:
首先先用一些比较简单的模型比如:线性回归,SVM进行训练,得出training loss,这个损失值可以作为一个标准。然后在换用一个更复杂的模型,如果损失值更高,则是optimization出问题,如果损失值变低,则是model bias有问题。
2.训练集损失函数小,测试集损失函数大
1.overfitting
产生过拟合的情况有很多,其中一般可以先考虑是否是模型弹性过于大。
解决这种方法有很多,下面进行举例:
- 增加更多的训练集
- 图像增强(左右翻转,部分放大)
- 限制模型(降低模型的自由度)
- 使用更少的特征数,共享超参数
- 提早结束训练
- 正则化
- Dropout(在前向传播的时候,让某个神经元的激活值以一定的概率p停止工作)
但是存在一个严重的问题:上面的解决方法,很多与解决model bias的方法相冲突
还有第二种原因: 在实际的工程中,有时标记的数据数量不足以留出验证样本,否则会导致训练样本的数量太少。
通用解决方法:
N-fold Cross Validation(N重交叉验证):
1.首先随机的将大小为m的总标记样本分为n个fold(子样本),通常每个子样本的大小相同为 m i = m n m_i=\frac{m}{n} mi=nm。
2.对于每一个子样本 m i m_i mi,算法在除了该子样本的所有子样本上训练,得到一个hypothesis,将得到的hypothesis在该子样本 m i m_i mi上进行test得到error。
3.最终在所有的hypothesis中选择error最小的hypothesis。
这里的error为cross-validation error,不是只在 m i m_i mi上test,而要在所有的fold中进行test并得到平均值:
2.mismatch
这种情况是训练集与测试集的分布不一样导致的
二、驻点(Critical Point)
1.局部最优(local minima)
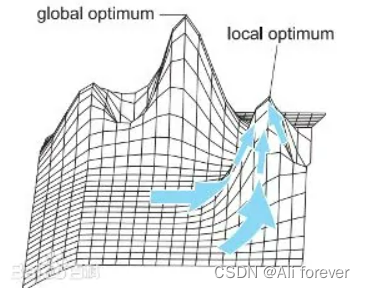 我们可以看到梯度下降时有可能会出现两个峰值点,这两个峰值点对照的都是梯度算子为0,这就说明有可能会出现低于最高峰值的点作为输出而结束训练,这种情况是不可取的,并没有达到最优解,这种峰值点就叫做局部最优(local minima),真正的峰值点叫做全局最优(global minima)
我们可以看到梯度下降时有可能会出现两个峰值点,这两个峰值点对照的都是梯度算子为0,这就说明有可能会出现低于最高峰值的点作为输出而结束训练,这种情况是不可取的,并没有达到最优解,这种峰值点就叫做局部最优(local minima),真正的峰值点叫做全局最优(global minima) 2.鞍点(Saddle Point)
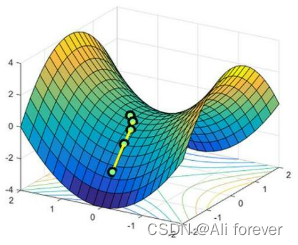 由于梯度下降时要求解凸函数的凸点,但是如果对于非凸函数,则会有可能存在这种鞍点(Saddle Point),这种点并不是我们所需要的。这种点的特点是在各个方向的梯度会有增有减,并不是最小。
由于梯度下降时要求解凸函数的凸点,但是如果对于非凸函数,则会有可能存在这种鞍点(Saddle Point),这种点并不是我们所需要的。这种点的特点是在各个方向的梯度会有增有减,并不是最小。 3.矩阵的泰勒展开与hessian矩阵
矩阵的泰勒展开式:
L ( θ ) = L ( θ ′ ) + ( θ − θ ′ ) T g ( θ ′ ) + 1 2 ( θ − θ ′ ) T H ( θ ′ ) ( θ − θ ′ ) L(\theta)=L(\theta')+(\theta-\theta')^Tg(\theta')+\frac{1}{2}(\theta-\theta')^TH(\theta')(\theta-\theta') L(θ)=L(θ′)+(θ−θ′)Tg(θ′)+21(θ−θ′)TH(θ′)(θ−θ′)
其中 g ( θ ′ ) = ∇ L ( θ ′ ) g(\theta')=\nabla L(\theta') g(θ′)=∇L(θ′), H ( θ ′ ) H(\theta') H(θ′)是hessian矩阵,其矩阵形式应为
H i j = ∂ 2 ∂ θ i ∂ θ j L ( θ ′ ) H_{ij}=\frac{\partial^2}{\partial\theta_i\partial\theta_j} L(\theta') Hij=∂θi∂θj∂2L(θ′)
我们现在研究的是如何分辨local minima还是saddle point,所以 g ( θ ′ ) = 0 g(\theta')=0 g(θ′)=0,并且令 θ − θ ′ = u \theta-\theta'=u θ−θ′=u,所以我们的矩阵泰勒展开式就化简为
L ( θ ) = L ( θ ′ ) + 1 2 u T H ( θ ′ ) u L(\theta)=L(\theta')+\frac{1}{2}u^TH(\theta')u L(θ)=L(θ′)+21uTH(θ′)u
首先hessian矩阵是一个对称矩阵,根据二次型的定义 u T H ( θ ′ ) u u^TH(\theta')u uTH(θ′)u是一个二次型矩阵,那么我们判断该点的类型时,就要利用该性质去进行判断
如果 u T H ( θ ′ ) u > 0 u^TH(\theta')u>0 uTH(θ′)u>0,即该矩阵是一个正定二次型时:
对任意的 θ ′ \theta' θ′而言,都有 L ( θ ) > L ( θ ′ ) L(\theta)>L(\theta') L(θ)>L(θ′),所以该点是local minima点
如果 u T H ( θ ′ ) u < 0 u^TH(\theta')u<0 uTH(θ′)u<0,即该矩阵是一个负定二次型时:
对任意的 θ ′ \theta' θ′而言,都有 L ( θ ) < L ( θ ′ ) L(\theta)<L(\theta') L(θ)<L(θ′),所以该点是local maxima点
如果 u T H ( θ ′ ) u 符号不定时 u^TH(\theta')u符号不定时 uTH(θ′)u符号不定时,即该矩阵是一个二次型时:
该点是saddle point点
解决鞍点的办法:只需要计算出 u T H ( θ ′ ) u > 0 u^TH(\theta')u>0 uTH(θ′)u>0的 θ ′ \theta' θ′,然后往这个方向去调整值就能逃出saddle point的陷阱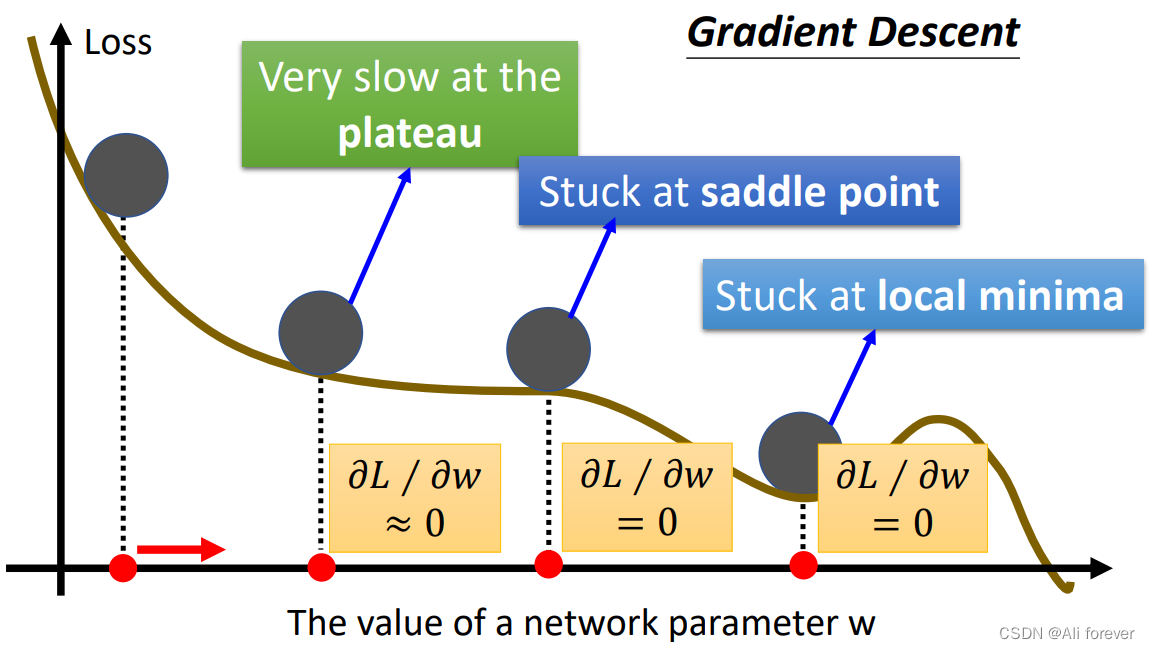
三、批量梯度下降(batch)和动量(momentum)
我们在之前就说过,要对训练集进行拆分训练,那么这是为什么呢?大的batch与小的batch有啥优缺点呢?下面我们将讨论一下
1.batch的大小优劣
- 时间
我们会主观的以为,如果batch太大,会导致训练一次的时间过长,其实并不是,因为现在已经多数运用GPU去进行训练,能够实现并行地训练,事实上,大的batch训练时间反而会比小的batch时间要小。这是因为在一个epoch中,小batch虽然update的时间更短,但需要update的次数更多,花费的时间反而更多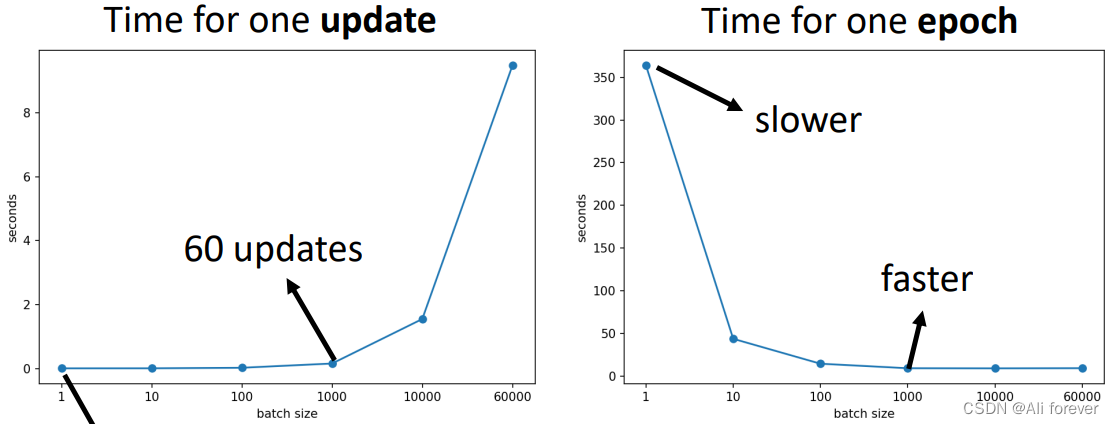
- 噪声
由于小batch更新的次数远远超过大batch的情况,所以无可避免地引入了更多噪声,所以大batch的噪声会更小。但是噪声更小并不代表有更高的准确率,事实上在训练中引入适当的噪声可以大大提高神经网络的健壮性,能让其在测试集时抗噪声能力更强,准确率更高。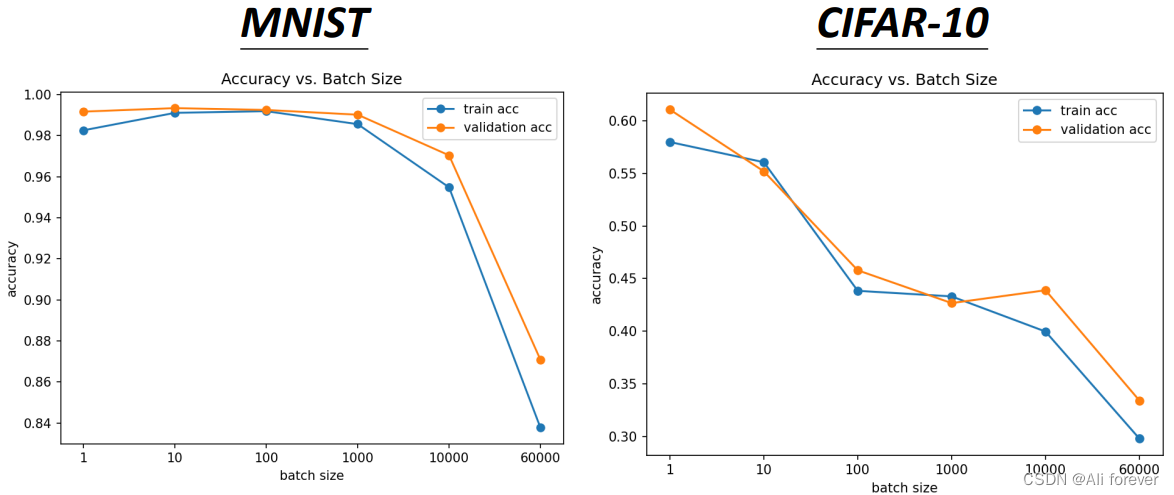
实际上,由于在一次epoch中更新的次数更多,所以小batch更不容易到达所谓的local minima跟saddle point,这是因为每次更新完都会获得新的一条曲线。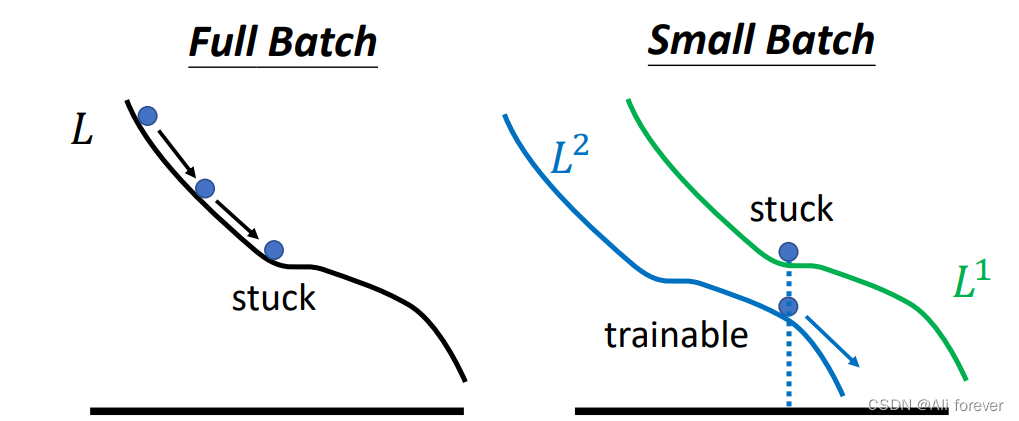
总的来说,小batch的泛化能力更强,最优化遇到的问题也更少,不容易产生过拟合。
2.动量(momentum)
我们在计算梯度下降的方向时,为了提高准确率,避免陷入critical point的陷阱时,可以引入动量这个概念去配合梯度下降去进行训练。
所谓的动量也就是在本次梯度下降的方向上加上上一次梯度下降的方向。
假设第1次的梯度方向为 g 1 g^1 g1,动量方向为 m 1 m^1 m1,参数为 θ 1 \theta^1 θ1很明显第二次的动量 m 2 = λ m 1 − η g 1 m^2=\lambda m^1- \eta g^1 m2=λm1−ηg1,那么第二次的参数就为 θ 2 = θ 1 + m 2 \theta^2=\theta^1+m^2 θ2=θ1+m2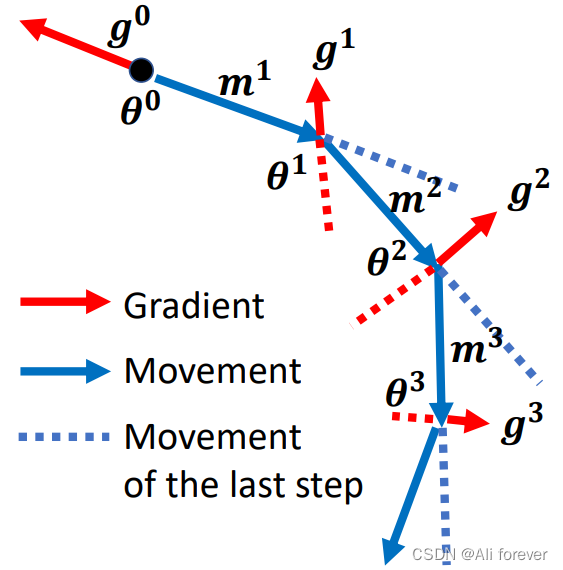
最后我们发现动量m其实是前面所有梯度方向的加权值
四、学习率(learning rate)
有很多时候,其实critical point的问题并不是主要的问题,还有一个更加主要的问题,就是我们所设置的学习率。学习率太大,会导致每次更新的太过于夸张,从而产生振荡,学习率太小,又无法很好地更新的我们的参数,所以如何调整我们的学习率成了一个很重要的问题
1.自适应梯度算法(Adagrad)
θ t + 1 = θ t − η σ i t g i t \theta^{t+1}=\theta^t-\frac{\eta}{\sigma_i^t}g_i^t θt+1=θt−σitηgit
其中 σ i t = 1 t + 1 ∑ i = 0 t ( g i t ) 2 \sigma_i^t=\sqrt{\frac{1}{t+1}\sum_{i=0}^t(g_i^t)^2} σit=t+11∑i=0t(git)2
Adagrad的缺点是虽然不同变量有了各自的学习率,但是初始的全局学习率还是需要手工指定。如果全局学习率过大,优化同样不稳定;而如果全局学习率过小,因为Adagrad的特性,随着优化的进行,学习率会越来越小,很可能还没有到极值就停滞不前了。
2.RMSProp
RMSProp算法修改了Adagrad的梯度平方和累加为指数加权的移动平均,使得其在非凸设定下效果更好
θ t + 1 = θ t − η σ i t g i t \theta^{t+1}=\theta^t-\frac{\eta}{\sigma_i^t}g_i^t θt+1=θt−σitηgit
其中 σ i t = α ( σ i t − 1 ) 2 + ( 1 − α ) ( g i t ) 2 \sigma_i^t=\sqrt{\alpha(\sigma_i^{t-1})^2+(1-\alpha)(g_i^t)^2} σit=α(σit−1)2+(1−α)(git)2
之前的梯度下降值对 σ i t \sigma_i^t σit有更大的影响,而现在的梯度下降值则影响没有这么大。
但是RMSProp依然是要依靠自己设定的初始全局学习率
3.Adam(适应性矩估计)
Adam是RMSProp与Momentum的结合体
θ t + 1 = θ t − η v t ^ + ξ m t ^ \theta^{t+1}=\theta^t-\frac{\eta}{\sqrt {\hat{v_t}}+\xi}\hat{m_t} θt+1=θt−vt^+ξηmt^
其中 m t ^ = m t 1 − β 1 t { {\hat{m_t}}}=\frac{m_t}{1-{\beta_1}^t} mt^=1−β1tmt, v t ^ = v t 1 − β 2 t { {\hat{v_t}}}=\frac{v_t}{1-{\beta_2}^t} vt^=1−β2tvt
而 m t = β 1 m t − 1 + ( 1 − β 1 ) g t − 1 m_t=\beta_1m_{t-1}+(1-\beta_1)g_{t-1} mt=β1mt−1+(1−β1)gt−1, v t = β 2 v t − 1 + ( 1 − β 2 ) g t − 1 2 v_t=\beta_2v_{t-1}+(1-\beta_2){g_{t-1}}^2 vt=β2vt−1+(1−β2)gt−12
这种方法并不会抵消分子和分母的变化,因为动量改变的是方向,而分母只改变是模值,也就是大小
Adam梯度经过偏置校正后,每一次迭代学习率都有一个固定范围,使得参数比较平稳。
结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点
为不同的参数计算不同的自适应学习率
也适用于大多非凸优化问题——适用于大数据集和高维空间。
Adam相对于SGDM来说,一开始训练的下降速度很快,但是到后期会被SGD超越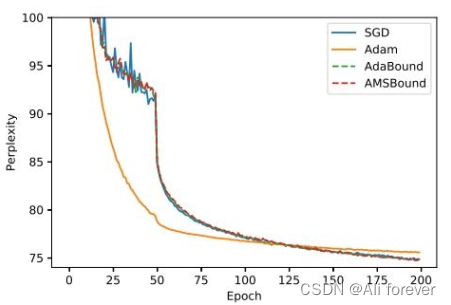
Adam相对于SGDM来说,在验证集上面的表现会比较差,并且不大稳定
4.Learning rate scheduling
我们前面都是让学习率 η \eta η固定,这样子会导致接近训练完成时振荡,我们可以让学习率随时间动起来,下面提供两种方法。
Learning Rate Decay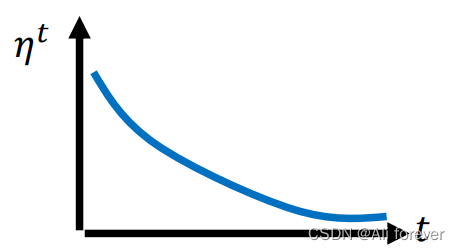
Warm Up
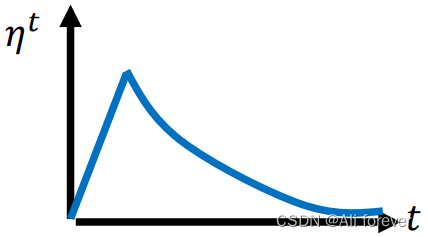
5.SWATS
上面我们了解到Adam一开始速度很快,然后SGDM再结束时较于平稳,那么我们就要找一种方式把他们给结合起来。但结合起来有个最困难的地方,那就是在切换时,如何校正 η \eta η的值,这是一个很难的问题
但这种方法是自己随机设置的值,有很强的主观性。
6.AMSGrad
由于Adam中有可能因为学习率为负数而导致最后结果不收敛,所以有一种比较新颖的方法叫做AMSGrad能保证学习率一直为正数。 v t ^ = max ( v t − 1 ^ , v t ) \hat{v_t}=\max(\hat{v_{t-1}},v_t) vt^=max(vt−1^,vt),当然这种做法的学习率一直会比较小。
总结
本文介绍了分析问题与调参的理论部分,希望大家能从中获取到想要的东西,下面附上一张思维导图帮助记忆。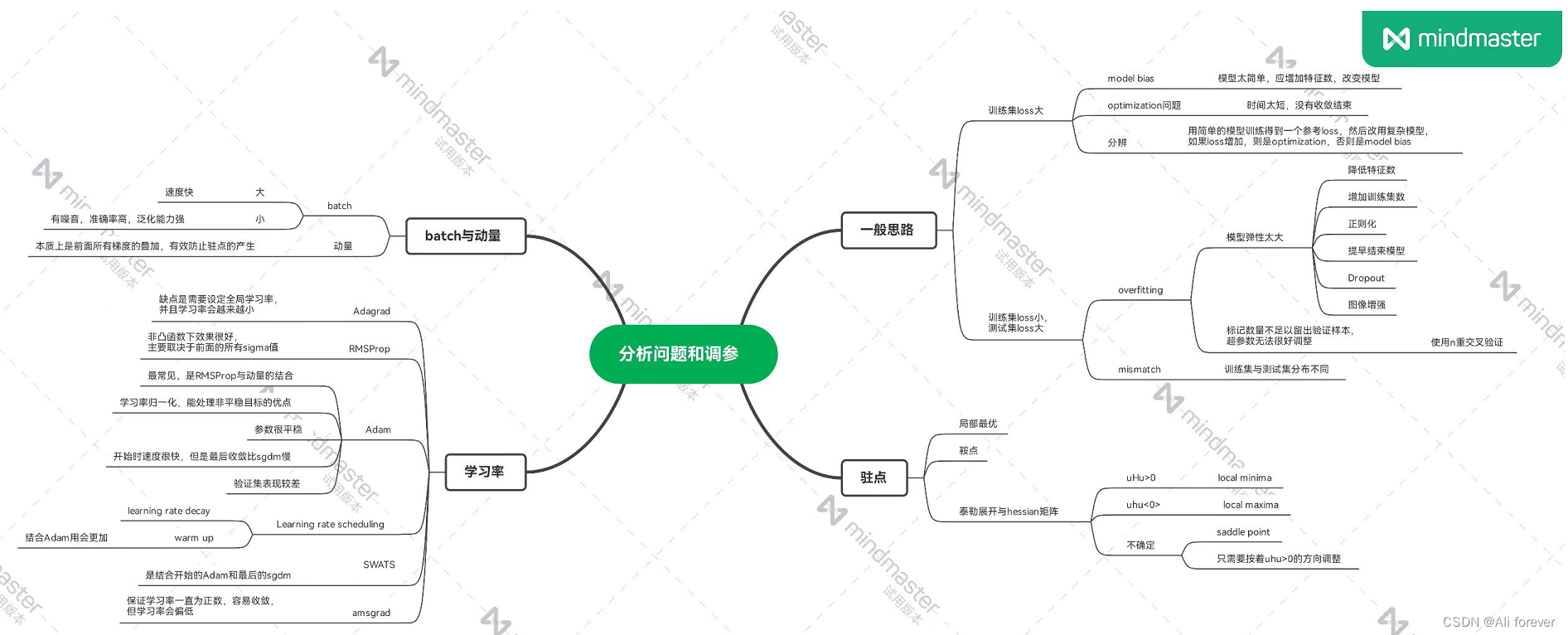
边栏推荐
- Android 开发用 Kotlin 编程语言 二 条件控制
- Android development with Kotlin programming language - basic data types
- 脱光衣服待着就能减肥,当真有这好事?
- DocuWare平台——文档管理的内容服务和工作流自动化的平台详细介绍(下)
- 华为分析&联运活动,助您提升游戏总体付费
- hdu4545 魔法串
- 012_SSS_ Improving Diffusion Model Efficiency Through Patching
- 反射修改jsessionid实现Session共享
- A small test of basic grammar, Go lang1.18 introductory refining tutorial, from Bai Ding to Hongru, basic grammar of go lang and the use of variables EP02
- Http-Sumggling缓存漏洞分析
猜你喜欢
随机推荐
Microcontroller: temperature control DS18B20
微服务结合领域驱动设计落地
今天告诉你界面控件DevExpress WinForms为何弃用经典视觉样式
trie树模板
PCB layout must know: teach you to correctly lay out the circuit board of the op amp
提问题进不去。想问大家一个关于返回值的问题(图的遍历),求给小白解答啊
自定义过滤器和拦截器实现ThreadLocal线程封闭
PG优化篇--执行计划相关项
How OpenHarmony Query Device Type
nyoj754 黑心医生 结构体优先队列
Import Excel/CSV from Sub Grid within Dynamics 365
可视化开发必看:智慧城市四大核心技术
365天挑战LeetCode1000题——Day 050 在二叉树中增加一行 二叉树
用KUSTO查询语句(KQL)在Azure Data Explorer Database上查询LOG实战
提取人脸特征的三种方法
机器学习——集成学习
Chapter 4: activiti RuntimeService settings get and get process variables, and the difference from taskService, set process variables when starting and completing tasks [easy to understand]
012_SSS_ Improving Diffusion Model Efficiency Through Patching
uniapp中的view高度设置100%
一张图看懂 SQL 的各种 join 用法!