当前位置:网站首页>On the calculation of non interaction polarizability
On the calculation of non interaction polarizability
2020-11-09 11:37:00 【open_22rhv8iu】
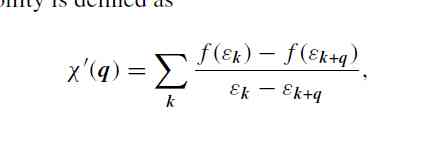
First , We need to sample evenly in the Brillouin zone , Generate a series of uniform points , Because of the uniform sealing , Given k and q after ,k+q It can be expressed by the existing points . It should be noted that , We need to deal with out of scope k+q Do the translation of the point ( Take the mold with the number )
after , Then we can calculate the polarizability . It's equivalent to using discrete coordinates here .
For two-dimensional systems, the time complexity is O(N^4), C++ 1 Seconds can count 10^7 Time ,200*200 De lattice point ,C++ Probably need 160 The second time , The actual time is 303.249s
square lattice matlib Code
nx = 100;
ny = 100;
kx = linspace(0,2*pi,nx);
ky = linspace(0,2*pi,ny);
[KX,KY] = meshgrid(kx,ky);
E = -(cos(KX) + cos(KY));
%mesh(KX,KY,E);
mu = 0;
T = 0.001;
delta = 0.01*0; % Small void part
chi = zeros(nx,ny);
Ef=0;
%[C,h] = contour(KX,KY,E,[Ef,0,0]);
for i = 1:nx
for j = 1:ny
for k=1:nx
for l=1:ny
index_kq_x = mod(i+k,nx)+1;
index_kq_y = mod(j+l,ny)+1;
Ek = E(k,l);
Ekq = E(index_kq_x,index_kq_y);
chi(i,j) = chi(i,j) + (Fermi_funtion(Ek,mu,T)-Fermi_funtion(Ekq,mu,T))/(Ek-Ekq+1i*delta);
end
end
end
end
mesh(KX,KY,-real(chi))
It's very slow
C++ Code
#include <iostream>
#include <cmath>
#include <vector>
#include <fstream>
#include <iomanip>
#include <complex>
#include <ctime>
using namespace std;
#define PI 3.1415926
vector<double> linspace(double min, double max, int n){
vector<double> result;
// vector iterator
int iterator = 0;
for (int i = 0; i <= n-2; i++){
double temp = min + i*(max-min)/(floor((double)n) - 1);
result.insert(result.begin() + iterator, temp);
iterator += 1;
}
//iterator += 1;
result.insert(result.begin() + iterator, max);
return result;
}
double fermi_function(double E,double mu,double T){
return 1/(exp((E-mu)/T)+1);
}
int main()
{
int nx = 200, ny = 200;
double mu = 0;
double T = 0.026;
double delta = 0.01;
vector<double> kx = linspace(0,2*PI,nx);
vector<double> ky = linspace(0,2*PI,ny);
vector<vector<double>> E(nx,vector<double>(ny,0));
vector<vector<complex<double>>> chi(nx,vector<complex<double>>(ny));
vector<vector<double>> real_chi(nx,vector<double>(ny,0));
clock_t startTime,endTime;
startTime = clock(); // Timing begins
cout<<"start run"<<endl;
for(int i=0;i<nx;i++){
for(int j=0;j<ny;j++){
E[i][j] = -(cos(kx[i])+cos(ky[i]));
}
}
for(int i=0;i<nx;i++){
for(int j=0;j<ny;j++){
for(int k=0;k<nx;k++){
for(int l=0;l<nx;l++){
int index_kq_x = (i+k)%nx;
int index_kq_y = (j+l)%ny;
double Ek = E[k][l];
double Ekq = E[index_kq_x][index_kq_y];
double f1 = fermi_function(Ek,0,T);
double f2 = fermi_function(Ekq,0,T);
if(k!=index_kq_x&&l!=index_kq_y){
chi[i][j] += (f1-f2)/(Ek-Ekq+1i*delta);
}
}
}
}
}
ofstream out("Datachi.txt");
for(int i=0;i<nx;i++){
for(int j=0;j<ny;j++){
out<<fixed<<setprecision(4)<<chi[i][j].real()<<" ";
}
out<<endl;
}
endTime = clock();// End of the timing
cout << "The run time is: " <<(double)(endTime - startTime) / CLOCKS_PER_SEC << "s" << endl;
}
Python Drawing script
import numpy as np
import matplotlib.pyplot as plt
from math import pi
file = open("Datachi.txt", "r")
row = file.readlines()
list_text = []
for line in row:
line = list(line.strip().split(' '))
s = []
for i in line:
s.append(float(i))
list_text.append(s)
#print(list_text)
nx = 10
ny = 10
chi = np.array(list_text)
kx = np.linspace(0,2*pi,nx)
ky = np.linspace(0,2*pi,ny)
KX, KY = np.meshgrid(kx, ky)
#plt.contourf(KX,KY,chi)
#plt.show()
fig = plt.figure(figsize=plt.figaspect(0.5))
ax = fig.add_subplot(1, 2, 1, projection='3d')
surf = ax.plot_surface(KX, KY, chi, rstride=1, cstride=1, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
ax.set_zlim(-1.01, 1.01)
fig.colorbar(surf, shrink=0.5, aspect=10)
plt.show()
版权声明
本文为[open_22rhv8iu]所创,转载请带上原文链接,感谢
边栏推荐
- Learning notes of nodejs
- 使用流读文件写文件处理大文件
- EFF 认为 RIAA 正在“滥用 DMCA”来关闭 YouTube-DL
- Python零基础入门教程(01)
- VisualStudio(Mac)安装过程笔记
- List of wechat video Number broadcasters October 2020
- Handwritten digital image recognition convolution neural network
- 十五年后,重构一个“在线的腾讯”
- android studio创建平板模拟器方法
- 在企业的降本增效诉求下,Cube如何助力科盾业务容器化“一步到位”?
猜你喜欢
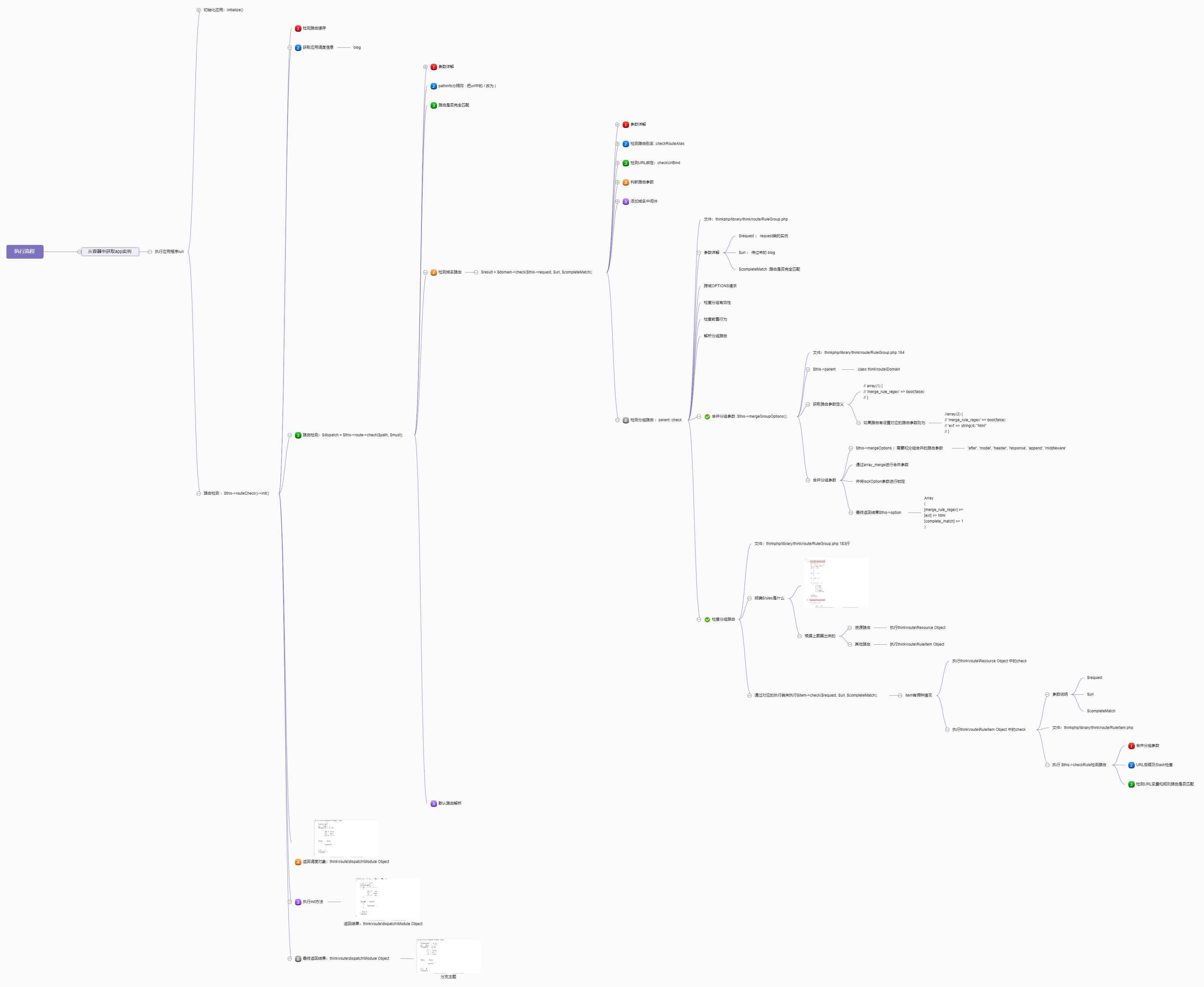
Source code analysis of ThinkPHP framework execution process

Kubernetes业务日志收集与监控
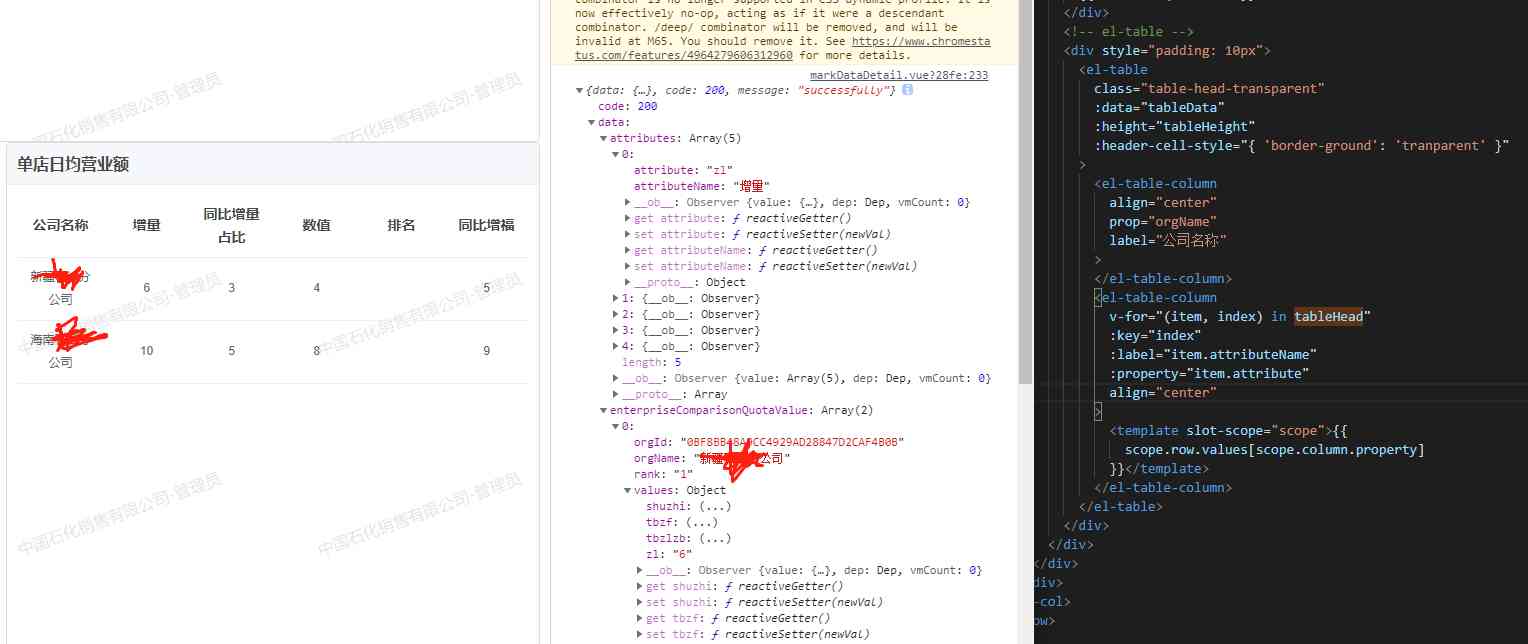
El table dynamic header

From the practice, this paper discusses the problems caused by the inconsistent design of ruby syntax.

关于无相互作用极化率的计算

ThinkPHP框架执行流程源码解析
块级元素和行内元素

使用CopyMemory API出现 尝试读取或写入受保护的内存。这通常指示其他内存已损坏。
微信视频号播主排行榜2020年10月
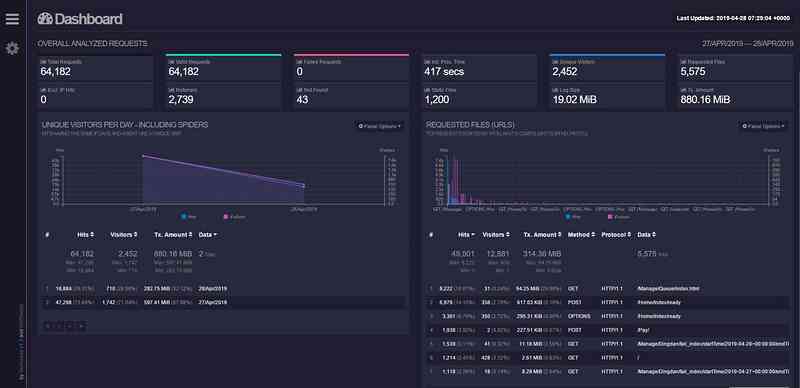
Log analysis tool - goaccess
随机推荐
Recommended tools for Mac
jsliang 求职系列 - 08 - 手写 Promise
Mapstructure detoxifies object mapping
抢球鞋?预测股市走势?淘宝秒杀?Python表示要啥有啥
Front end code style practice prettier + eslint + git hook + lint staged
一个简单的能力,决定你是否会学习!
Git delete IML file
android studio创建平板模拟器方法
Impact of libssl on CentOS login
手写Koa.js源码
range_sensor_layer
Jsliang job series - 08 - handwritten promise
Large scale project Objective-C - nsurlsession access SMS verification code application example sharing
配置交换机Trunk接口流量本地优先转发(集群/堆叠)
From coding, network transmission, architecture design, Tencent cloud high quality, high availability real-time audio and video technology practice
详解Python input()函数:获取用户输入的字符串
inet_pton()和inet_ntop()函数详解
Python零基础入门教程(01)
典型分布式系统分析:Dynamo
Program life: from Internet addicts to Microsoft, bat and byte offer harvesters