当前位置:网站首页>第二十六章:二维数组
第二十六章:二维数组
2022-08-02 14:10:00 【WANGHAOXIN364】
二维数组
问题描述:给定一个N行M列的矩阵,将其逆序输出(行和列都倒着输出)。
样例:
输入数据#1
3 4
1 2 3 4
4 5 6 7
5 6 7 8
Copy
输出数据#1
8 7 6 5
7 6 5 4
4 3 2 1
Copy
算法思路:定义N个一维数组,每个数组存储一行,然后倒着讲这些一维数组逆序输出。
问题:如何定义N个大小为M的一维数组?在程序中又将如何访问?
一、二维数组的定义
当一维数组元素的类型也是一维数组时,便构成了“数组的数组”,即二维数组。二维数组定义的一般格式:
dataType arrayName[length1][length2];
Copy
其中, dataType 为数据类型, arrayName 为数组名, length1 为第一维下标的长度, length2 为第二维下标的长度。
我们可以将二维数组看做一个 Excel 表格,有行有列,length1 表示 行数 ,length2 表示列数,要在二维数组中定位某个元素,必须同时指明行和列。
例如:
int a[4][6];
Copy

二、二维数组元素的引用
二维数组的数组元素引用与一维数组元素引用类似,区别在于二维数组元素的引用 必须给出两个下标 。
引用的格式为:
arrayName[length1][length2];
Copy
例如:
int a[3][4];
Copy
定义了一个 3 行 4 列的二维数组,共有 3×4=12 个元素,数组名为 a,即:
a[0][0], a[0][1], a[0][2], a[0][3]
a[1][0], a[1][1], a[1][2], a[1][3]
a[2][0], a[2][1], a[2][2], a[2][3]
Copy
二维数组的行下标和列下标都从0开始;如果想表示第 1行第 1 列的元素,应该写作 a[0][0],第n行第m列对应数组元素a[n-1][m-1]。
a[2][3]即表示第3行第4列的元素。
三、二维数组的初始化
初始化为0:
① 定义为全局变量,定义为全局变量的二维数组默认会被初始化为0。
② int a[N][M]= {0}; 将所有N*M个元素全部初始化为0(只有初始化为0可以这么写)。
初始化为其他值:
① 全部初始化: 二维数组的每一行是一个一维数组,可以按照一维数组的方式初始化,最外层再加一个大括号“{}”。
示例1:int a[3][2] = { {1, 2}, {4, 5}, {7, 8} } ; (内部大括号之间由英文逗号分隔)。
示例2:char c[3][2] = { {'a', 'b'}, {'c', 'd'}, {'e', 'f'} } ;
② 部分初始化:
示例:int a[3][3] = { {1, 2}, {4, 5} }; (初始化第0行和第1行的前2个元素)。
四、二维数组的输入输出
二维数组的输入:

示例:读取3行2列的整数矩阵,存储到二维数组中:
int a[5][5];
for(int i=1; i<=3; i++)
{
for(int j=1; j<=2; j++)
{
cin>>a[i][j];
}
}
Copy
二维数组的输出:

将上述矩阵保持原来的行和列原样输出。
int a[5][5];
for(int i=1; i<=3; i++)
{
for(int j=1; j<=2; j++)
{
cout<<a[i][j];
}
}
Copy
五、逆序输出矩阵

const int N=101,M=101;
int n,m,a[N][M];
int main()
{
cin>>n>>m;
for(int i=1; i<=n; i++)//从上往下一行一行读取
{
for(int j=1; j<=m; j++)//从左往右一列一列读取
{
cin>>a[i][j];//存放于指定位置
}
}
for(int i=n; i>=1; i--)//从最后一行往前读取
{
for(int j=m; j>=1; j--)//从最后一列往左读取
{
cout<<a[i][j];
}
}
return 0;
}
Copy
六、例题和练习
例 1 对角线输出:
已知一个n*n的矩阵(n<=20),把矩阵二条对角线上的元素值加上10,然后输出这两条新对角线上的所有元素之和。
注意当n为奇数时两条对角线交叉的那个元素改变时只需要改变一次,累加的时候需要累加两次
输入格式
第一行为一个整数n(n<=20)
第二行开始为一个n*n个整数组成的矩阵,整数范围(1-1000)
输出格式
输出一个整数,为矩阵两条新对角线上的元素之和
输入样例:
6
1 1 1 1 1 1
2 2 2 2 2 2
3 3 3 3 3 3
4 4 4 4 4 4
5 5 5 5 5 5
6 6 6 6 6 6
Copy
输出样例:
162
Copy
示例1:图为N = 6的矩阵,将两条对角线上的元素输出1,其余位置输出0

提示:使用二维数组存储矩阵元素,问题的核心是找出两条对角线所包含元素位置的规律。
分析:
① 右斜线(\):行=列,都从1到6(N)
a[1][1]
a[2][2]
...
a[6][6]
Copy
② 左斜线(/):行+列 = 7(N+1)
a[1][6]
a[2][5]
...
a[6][1]
Copy
代码详情:
const int N=25;//将N设置成固定不变的常量
int n,ans,a[N][N];
int main()
{
cin>>n;
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j++)
{
cin>>a[i][j];
}
}
for(int i=1; i<=n; i++)
{
ans+=a[i][i]; //累加右对角线元素
ans+=a[i][n+1-i]; //累加左对角线元素
}
ans+=2*n*10; //总共2n个元素,每个元素都+10
return 0;
}
Copy
示例2:杨辉三角
杨辉三角是一个由数字排列成的三角形表,一般形式如下:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
(第一列和每行最后一列都为1,其余数字为它的左上方和正上方数字之和)
输入一个正整数n(n≤20),表示三角形的行数,输出杨辉三角的第n行。
输入格式
输入一个整数n(n≤20)
输出格式
输出杨辉三角的第n行
输入样例:
6
Copy
输出样例:
1 5 10 10 5 1
Copy

杨辉三角具有以下特性:(关注黄色标注部分)
① 第1列元素的值全为1。
② 第i行拥有i个元素,即:第i行有i列。
③ 元素(i, j)通过元素(i-1, j-1)和(i-1, j)累加获得,即:a[i][j] = a[i-1][j-1] + a[i-1][j]。
④ 如果第0列元素全为0,那么第1列元素也满足特性③。
解题步骤:
① 定义二维数组a[N][N]存储杨辉三角,并初始化第0列为0(全局变量),a[1][1] = 1;
② 双层 for 循环,第 1 层for循环枚举行 i(2到N),第2层for循环枚举列 j(1到i);
③ 利用公式:a[i][j] = a[i-1][j-1] + a[i-1][j],计算a[i][j]的值。
④ 输出第N行的第1列到第N列。
const int N=101;
int n,a[N][N];
int main()
{
cin>>n;
a[1][1]=1;//第一行第一列:1
for(int i=2; i<=n; i++)
{
for(int j=1; j<=i; j++)//行与列相等
{
a[i][j]=a[i-1][j-1]+a[i-1][j];
}
}
for(int j=1; j<=n; j++)
{
cout<<a[n][j]<<" ";
}
return 0;
}
Copy
七、作业
边栏推荐
- pygame image rotate continuously
- MATLAB绘图函数fplot详解
- win10 system update error code 0x80244022 how to do
- Win10安装了固态硬盘还是有明显卡顿怎么办?
- 为vscode配置clangd
- 总结计算机网络超全面试题
- jest test, component test
- 发布模块到npm应该怎么操作?及错误问题解决方案
- casbin模型
- What should I do if the Win10 system sets the application identity to automatically prompt for access denied?
猜你喜欢
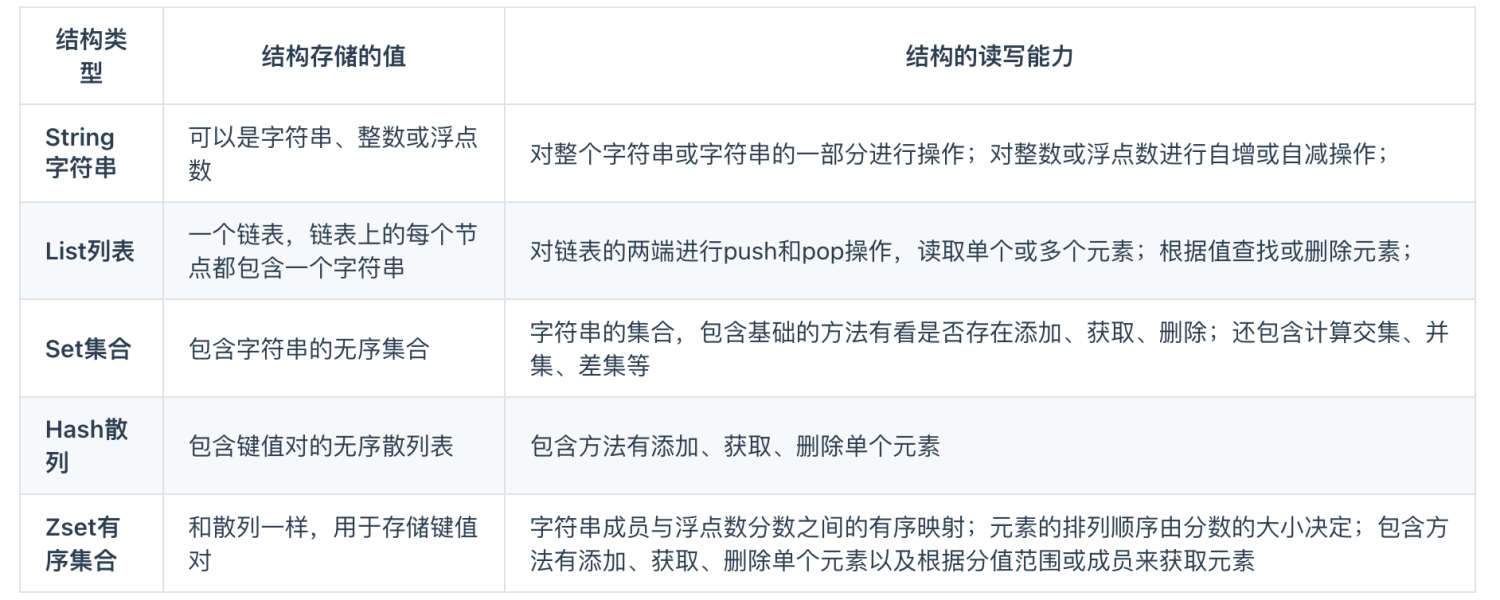
Redis常见面试题
Flink + sklearn - use JPMML implement flink deployment on machine learning model

Win11系统找不到dll文件怎么修复
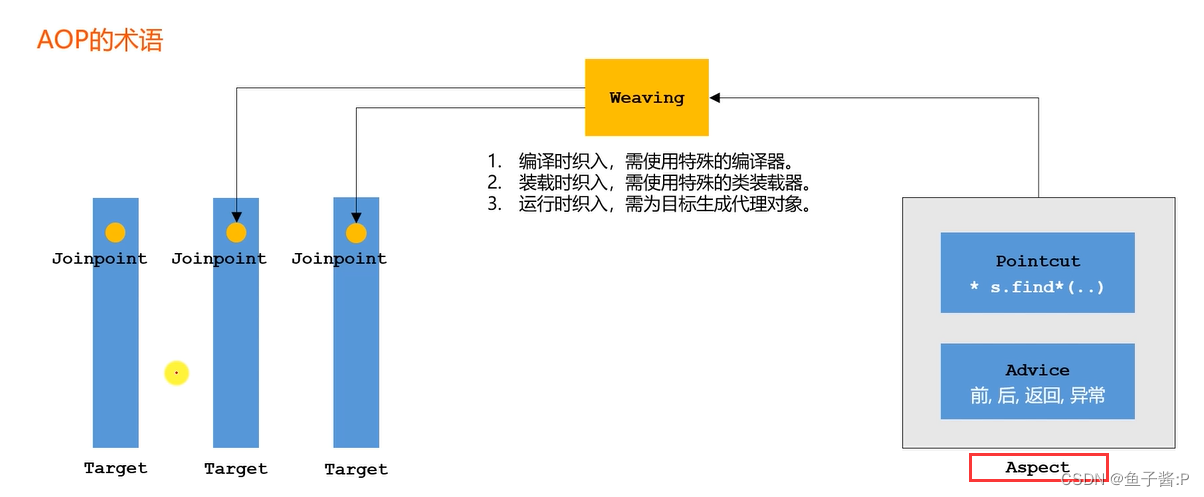
6.统一记录日志

Use tencent cloud builds a personal blog
What should I do if the Win10 system sets the application identity to automatically prompt for access denied?

How to solve Win11 without local users and groups
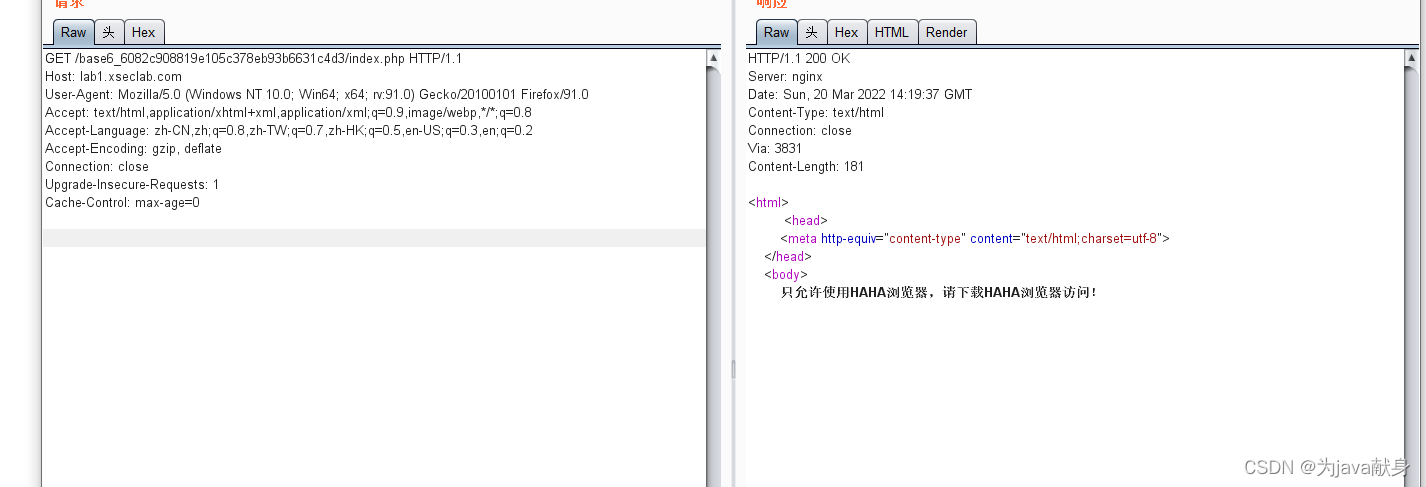
Network Security Packet Capture
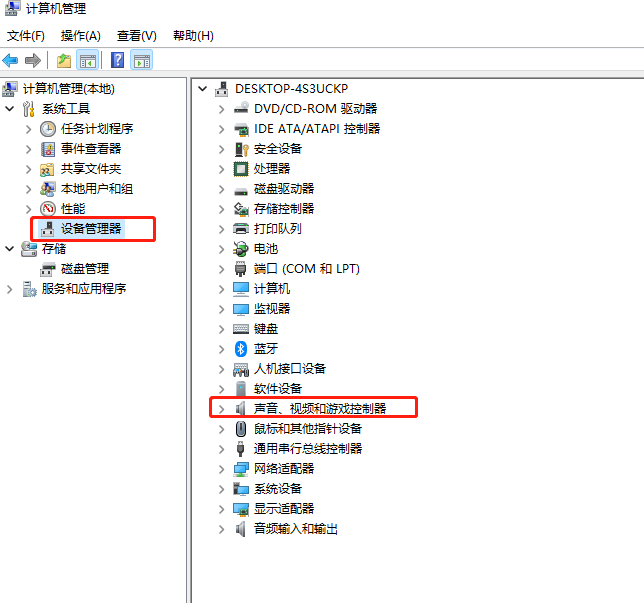
How to update Win11 sound card driver?Win11 sound card driver update method
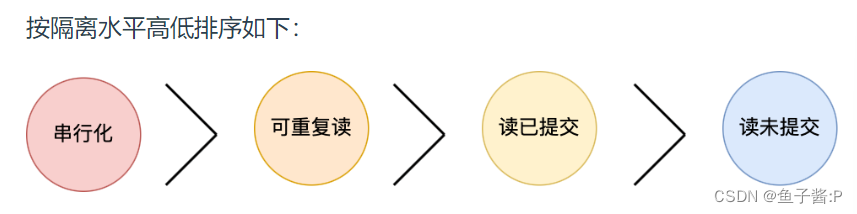
mysql学习总结 & 索引
随机推荐
win10无法直接用照片查看器打开图片怎么办
【STM32学习1】基础知识与概念明晰
Introduction to MATLAB drawing functions ezplot explanation
使用npx -p @storybook/cli sb init安装失败,手把手搭建专属的storybook
pygame image rotate continuously
网络安全抓包
yolov5官方代码解读——前向传播
倍增和稀疏表
Redis的线程模型
Mapreduce环境详细搭建和案例实现
Win11 keeps popping up User Account Control how to fix it
casbin模型
win10 system update error code 0x80244022 how to do
Mysql之MVCC
日常-笔记
STM32LL库使用——SPI通信
基于最小二乘法的线性回归分析方程中系数的估计
MATLAB绘图命令fimplicit绘制隐函数图形入门详解
Win10上帝模式干嘛的?Win10怎么开启上帝模式?
动态规划理论篇
