当前位置:网站首页>The 19th Zhejiang Provincial Collegiate Programming Contest VP记录+补题
The 19th Zhejiang Provincial Collegiate Programming Contest VP记录+补题
2022-07-07 21:50:00 【HeartFireY】
| A | B | C | D | E | F | G | H | I | J | K | L | M |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AC | AC | AC | – | – | WA/补题 | AC | – | AC | AC/待补 | – | AC | AC |
A.JB Loves Math
题目分析
现在有两个数字 a a a和 b b b,由你选择一个奇数 x x x和偶数 y y y,每次可以给 a a a加 x x x或减 y y y,问最小的操作次数将 a a a变为 b b b。
分类对差值进行讨论即可。
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
inline void solve(){
int a, b; cin >> a >> b;
int det = abs(a - b);
if(a == b) cout << 0 << endl;
else if(a > b && (det & 1 == 0) || a < b && det & 1) cout << 1 << endl;
else if(a < b && (det / 2) & 1 || a > b) cout << 2 << endl;
else cout << 3 << endl;
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
int t = 0; cin >> t;
while(t--) solve();
return 0;
}
B.JB Loves Comma
题目分析
找到cjb然后加个逗号就可以了,样例2好评
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
inline void solve(){
string str; cin >> str;
for(int i = 0; i < str.size(); i++){
if(i >= 2 && str[i] == 'b' && str[i - 1] == 'j' && str[i - 2] == 'c') cout << str[i] << ',';
else cout << str[i];
}
}
signed main(){
solve();
return 0;
}
C.JB Wants to Earn Big Money
题目分析
直接按照题意模拟,统计两类数量即可。
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
inline void solve(){
int n, m, X; cin >> n >> m >> X;
int ans = 0;
for(int i = 1; i <= n; i++){
int s; cin >> s;
if(s >= X) ans++;
}
for(int i = 1; i <= m; i++){
int s; cin >> s;
if(s <= X) ans++;
}
cout << ans << endl;
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
solve();
return 0;
}
F.Easy Fix
题目分析
主席树写挂了,赛时没调出来,我是菜狗
给定排列 p 1 , p 2 , p 3 , … , p n p_1, p_2, p_3,\dots, p_n p1,p2,p3,…,pn,定义 A i A_i Ai表示在 p i p_i pi左侧并比 p i p_i pi小的数字个数, B i B_i Bi表示在 p i p_i pi右侧并比 p i p_i pi小的数字个数, C i = min ( A i , B i ) C_i = \min(A_i, B_i) Ci=min(Ai,Bi)。现在给定多个操作 ( l , r ) (l, r) (l,r),求每个操作,交换 ( p i , p j ) (p_i, p_j) (pi,pj)后的 ∑ C i \sum C_i ∑Ci。
首先考虑如何处理初始时的 C i C_i Ci值,观察到以下性质:
- 对于 A i A_i Ai值的求解过程类似求逆序对的思想,可以直接上树状数组维护, O ( n log n ) O(n\log n) O(nlogn)求得全部的 A i A_i Ai
- 由于是排列, B i = p i − 1 − A i B_i = p_i - 1 - A_i Bi=pi−1−Ai可以 O ( 1 ) O(1) O(1)求得
- 那么 C i = min ( A i , B i ) C_i = \min(A_i, B_i) Ci=min(Ai,Bi)也是 O ( 1 ) O(1) O(1)得到的
由于每个询问相互独立,那么考虑交换 ( p l , p r ) (p_l, p_r) (pl,pr)操作对 C i C_i Ci的影响:
对于 [ 1 , l ) , ( r , n ] [1, l), (r , n] [1,l),(r,n]范围的数字, C i C_i Ci值一定不影响。因为交换操作均在单侧进行
对于 p l p_l pl,交换到 r r r位置后, A l → A l + 区 间 [ l , r ] 小 于 p l 的 数 字 个 数 A_l \rightarrow A_l + 区间[l,r]小于p_l的数字个数 Al→Al+区间[l,r]小于pl的数字个数, B l ’ B_l’ Bl’仍然可以直接求
对于 p r p_r pr,交换到 l l l位置后, A r → A r − 区 间 [ l , r ] 小 于 p r 的 数 字 个 数 A_r \rightarrow A_r - 区间[l ,r]小于p_r的数字个数 Ar→Ar−区间[l,r]小于pr的数字个数, B r ’ B_r’ Br’仍然可以直接求
如果我们在线询问(主席树维护),那么对于 p l , p r p_l,p_r pl,pr,实际上可以直接两个 O ( l o g n ) O(logn) O(logn)重新求。
那么重点是对于 [ l + 1 , r − 1 ] [l + 1, r - 1] [l+1,r−1]区间内的数字的 C i C_i Ci值变化,如何维护?
对于 p l ≤ p i ≤ p r p_l \leq p_i \leq p_r pl≤pi≤pr,如果 A i ≤ B i A_i \leq B_i Ai≤Bi,则交换后 A i − 1 , B i + 1 A_i - 1, B_i + 1 Ai−1,Bi+1,从而 C i − 1 C_i - 1 Ci−1
对于 p l ≥ p i ≥ p r p_l \geq p_i \geq p_r pl≥pi≥pr,如果 A i ≥ B i A_i \geq B_i Ai≥Bi,则交换后 A i + 1 , B i − 1 A_i + 1, B_i - 1 Ai+1,Bi−1,从而 C i − 1 C_i -1 Ci−1
对于 p l ≤ p i ≤ p r p_l \leq p_i \leq p_r pl≤pi≤pr,如果 A i − 1 ≥ B i + 1 , A i ≥ B i A_i - 1 \geq B_i + 1, A_i \geq B_i Ai−1≥Bi+1,Ai≥Bi,则交换后 C i + 1 C_i + 1 Ci+1
对于 p l ≥ p i ≥ p r p_l \geq p_i \geq p_r pl≥pi≥pr,如果 A i − 1 ≤ B i + 1 , A i ≤ B i A_i - 1 \leq B_i + 1, A_i \leq B_i Ai−1≤Bi+1,Ai≤Bi,则交换后 C i + 1 C_i + 1 Ci+1
那么对于以上四种情况,我们可以分别用四棵主席树进行维护。同时,对于 p l , p r p_l, p_r pl,pr的贡献计算还需要支持区间 < K <K <K的数字个数查询,因此共需五棵主席树进行维护,复杂度 O ( m × 4 log n ) O(m \times 4 \log n) O(m×4logn)。
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
const int N = 1e5 + 10;
int p[N], a[N], b[N], c[N], d[N];
using bset5 = std::bitset<5>;
namespace Fenwick{
int tree[N], len;
#define lowbit(x) ((x) & (-x))
inline void init(int ln){
len = ln; }
inline void update(int i, int x){
for(int pos = i; pos <= len; pos += lowbit(pos)) tree[pos] += x; }
inline int getsum(int i, int ans = 0){
for(int pos = i; pos; pos -= lowbit(pos)) ans += tree[pos]; return ans; }
}
namespace PresidentTree{
int root[N], sum[N << 5][5], lc[N << 5], rc[N << 5], cnt;
#define ls l, mid
#define rs mid + 1, r
void update(int &rt, int pre, int l, int r, int x, bset5 inc){
rt = ++cnt, lc[rt] = lc[pre], rc[rt] = rc[pre];
for(int i = 0; i <= 5; i++) sum[rt][i] = sum[pre][i] + (inc[i] ? 1 : 0);
if(l == r) return;
int mid = l + r >> 1;
if(x <= mid) update(lc[rt], lc[rt], l, mid, x, inc);
else update(rc[rt], rc[rt], mid + 1, r, x, inc);
}
int query(int st, int ed, int l, int r, int L, int R, int id){
if(l == L && r == R) return sum[ed][id] - sum[st][id];
int mid = l + r >> 1;
if(mid >= R) return query(lc[st], lc[ed], l, mid, L, R, id);
else if(mid >= L) return query(lc[st], lc[ed], l, mid, L, mid, id) + query(rc[st], rc[ed], mid + 1, r, mid + 1, R, id);
else return query(rc[st], rc[ed], mid + 1, r, L, R, id);
}
}
#define Pdt PresidentTree
inline void solve(){
int n = 0; std::cin >> n;
Fenwick::init(n);
for(int i = 1; i <= n; i++) std::cin >> p[i];
for(int i = 1; i <= n; i++){
a[i] = Fenwick::getsum(p[i]);
b[i]= p[i] - 1 - a[i];
Fenwick::update(p[i], 1);
c[i] = std::min(a[i], b[i]);
d[i] = d[i - 1] + c[i];
}
for(int i = 1; i <= n; i++){
bset5 flag; flag.reset();
if(a[i] <= b[i]) flag[1] = true;
if(a[i] >= b[i]) flag[3] = true;
if(a[i] - 1 >= b[i] + 1 && a[i] >= b[i]) flag[2] = true;
if(a[i] + 1 <= b[i] - 1 && a[i] <= b[i]) flag[4] = true;
flag[0] = true;
Pdt::update(Pdt::root[i], Pdt::root[i - 1], 1, n + 1, p[i], flag);
}
int m = 0; std::cin >> m;
while(m--){
int l, r; std::cin >> l >> r;
if(l == r){
std::cout << d[n] << endl; continue; }
else if(l > r) std::swap(l, r);
int ans = d[n] - c[l] - c[r];
if(p[l] < p[r]){
ans -= Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[l], p[r], 1)
- Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[l], p[r], 2);
} else {
ans -= Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[r], p[l], 3)
- Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[r], p[l], 4);
}
int nowa = Pdt::query(Pdt::root[0], Pdt::root[l - 1], 1, n + 1, 1, p[r], 0),
nowb = p[r] - 1 - nowa;
ans += std::min(nowa, nowb);
nowa = Pdt::query(Pdt::root[r], Pdt::root[n], 1, n + 1, 1, p[l], 0),
nowb = p[l] - 1 - nowa;
ans += std::min(nowa, nowb);
std::cout << ans << endl;
}
}
signed main(){
std::ios_base::sync_with_stdio(false), std::cin.tie(0);
solve();
return 0;
}
G.Easy Glide
题目分析
给定二维平面上的起点终点,以及 n n n个滑雪点,从起点出发以 v 1 v_1 v1速度行走,到达 n n n个滑雪点中的某个点后可以以 v 2 v_2 v2行走 3 s 3s 3s,然后变回 v 1 v_1 v1。要求求起点到终点的最短时间。
起点设为 0 0 0点,终点设为 n + 1 n + 1 n+1点,起点向其他点建满边,然后所有点向终点建边,然后 n n n个点相互建满边,边权均为时间。然后 d i j s k t r a dijsktra dijsktra求 0 0 0到 n + 1 n + 1 n+1最短路即可。
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e3 + 10;
struct node{
int x, y;
}p[N], st, ed;
struct edge{
int v;
double dis;
};
vector<edge> g[N];
int vis[10005];
inline double getdis(node x, node y){
double ans = sqrt((x.x - y.x) * (x.x - y.x) + (x.y - y.y) * (x.y - y.y));
return ans;
}
struct nd{
int v;
double dis;
const bool operator< (const nd &x) const {
return dis > x.dis; }
};
double dis[1100];
int n = 0;
double dijkstra(){
priority_queue<nd> pq;
pq.emplace(nd{
0, 0});
while(pq.size()){
auto [u,ww] = pq.top(); pq.pop();
if(vis[u]) continue;
vis[u] = 1, dis[u] = ww;
for(auto [v,w] : g[u]){
if(vis[v]) continue;
pq.emplace(nd{
v, ww + w});
}
}
return dis[n + 1];
}
inline void solve(){
cin >> n;
for(int i = 1; i <= n; i++){
int x, y; cin >> p[i].x >> p[i].y;
}
cin >> st.x >> st.y >> ed.x >> ed.y;
double v1, v2; cin >> v1 >> v2;
for(int i = 1; i <= n; i++){
g[0].emplace_back(edge{
i, getdis(st, p[i]) / v1});
}
g[0].emplace_back(edge{
n + 1, getdis(st, ed) / v1});
for(int i = 1; i <= n; i++){
double diss = getdis(p[i], ed), time = 0;
if(diss / v2 > 3.0) time += 3.0, diss -= v2 * 3, time += diss / v1;
else time = diss / v2;
//cout << i << "->" << "ed" << time << endl;
g[i].emplace_back(edge{
n + 1, time});
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
double diss = getdis(p[i], p[j]), time = 0;
if(diss / v2 > 3.0) time += 3.0, diss -= v2 * 3, time += diss / v1;
else time = diss / v2;
g[i].emplace_back(edge{
j, time});
}
}
cout << dijkstra() << endl;
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
cout<<fixed<<setprecision(12);
solve();
return 0;
}
I.Barbecue
题目分析
给定字符串,每次可以从两端选择1个字符删除,如果操作完后变成回文串则输。
显然,需要先判断是否一开始就是回文串,这里可以直接上哈希判。
接下来,如果一开始不是回文,我们会发现性质:
- 如果当前字符串删掉一端的 1 1 1个字符就会变成回文,那么一定选择另一端的删除。那么答案与长度奇偶性相关
- 如果两端删掉都是会变回文,那么当前必败
- 但可以发现两端删掉都会变回文时,字符串长度必为偶数,此时满足奇偶性规律。
Code
#include <bits/stdc++.h>
#define int long long
#define unt unsigned long long
#define endl '\n'
using namespace std;
const unt N = 1e6 + 10, base = 233233, MOD = 1e9 + 7;
unt hashp[N], hash_s1[N], hash_s2[N];
inline void init(){
hashp[0] = 1;
for(int i = 1; i <= N - 5; i++){
hashp[i] = hashp[i - 1] * base;
}
}
inline int check(int l, int r){
unt hash_val1 = hash_s1[r] - hash_s1[l - 1] * hashp[r - l + 1];
unt hash_val2 = hash_s2[l] - hash_s2[r + 1] * hashp[r - l + 1];
return hash_val1 == hash_val2;
}
inline void solve(){
int n, q; cin >> n >> q;
string s; cin >> s; s = '@' + s;
for(int i = 1; i <= n; i++) hash_s1[i] = hash_s1[i - 1] * base + s[i];
for(int i = n; i >= 1; i--) hash_s2[i] = hash_s2[i + 1] * base + s[i];
while(q--){
int l, r; cin >> l >> r;
if(l == r || check(l, r)) cout << "Budada\n";
else if((r - l + 1) & 1) cout << "Putata\n";
else cout << "Budada\n";
}
}
signed main(){
init();
ios_base::sync_with_stdio(false), cin.tie(0);
solve();
return 0;
}
J.Frog
计算几何,神犇队友写的,待补。放个代码:
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define ull unsigned long long
using namespace std;
const ull base = 13331;
const int N = 6;
const double pi=acos(-1);
int n,q,x,y;
inline void init(){
}
bool fk1(){
for(int i=(x+1)%360,cnt=1,j=(x+359)%360;cnt<=90;cnt++,i=(i+1)%360,j=(j+359)%360){
if(i==y||j==y)return true;
}
return false;
}
int getrotate(){
for(int i=(x+1)%360,cnt=1,j=(x+359)%360;cnt<=360;cnt++,i=(i+1)%360,j=(j+359)%360){
if(j==y)return -cnt;
if(i==y)return cnt;
//cout<<i<<" "<<j<<endl;
}
return 0;
}
bool ck(double x,double y){
return x*x+y*y>=1;
}
pair<double,double> nmb(double sx,double sy,double tx,double ty){
double midx=(sx+tx)/2,midy=(sy+ty)/2;
double d1=sqrt((midx-sx)*(midx-sx)+(midy-sy)*(midy-sy)),d2=sqrt(1-d1*d1);
double dx=sx-midx,dy=sy-midy,ansx=dy*d2/d1,ansy=dx*d2/d1;
//cout<<"???"<<midx<<" "<<midy<<" "<<ansx<<" "<<ansy<<endl;
if(ck(ansx+midx,ansy-midy)){
return {ansx+midx,midy-ansy};
}
else{
return {midx-ansx,midy+ansy};
}
}
inline void solve(){
cin>>x>>y;
double stx=cos(pi*x/180),sty=sin(pi*x/180),edx=cos(pi*y/180),edy=sin(pi*y/180);
if(x==y){
cout<<"0\n"<<stx<<" "<<sty<<endl;
return;
}
int d=getrotate();
if(abs(d)<=90){
cout<<"2\n";
cout<<stx<<" "<<sty<<endl;
cout<<(stx+edx)<<" "<<sty+edy<<endl;
cout<<edx<<" "<<edy<<endl;
}
else if((abs(d))<=131){
cout<<"3\n";
cout<<stx<<" "<<sty<<endl;
if(d>0){
double nowx=stx-sty,nowy=sty+stx;
cout<<stx-sty<<" "<<sty+stx<<endl;
auto [u,v]=nmb(nowx,nowy,edx,edy);
cout<<u<<" "<<v<<endl;
}
else{
double nowx=stx+sty,nowy=sty-stx;
cout<<stx+sty<<" "<<sty-stx<<endl;
auto [u,v]=nmb(nowx,nowy,edx,edy);
cout<<u<<" "<<v<<endl;
}
cout<<edx<<" "<<edy<<endl;
}
else{
cout<<"4\n";
cout<<stx<<" "<<sty<<endl;
if(d>0){
double nowx=-sty,nowy=stx;
cout<<stx-sty<<" "<<sty+stx<<endl;
cout<<-sty<<" "<<stx<<endl;
cout<<(nowx+edx)<<" "<<nowy+edy<<endl;
}
else{
cout<<stx+sty<<" "<<sty-stx<<endl;
cout<<sty<<" "<<-stx<<endl;
double nowx=sty,nowy=-stx;
//cout<<"???"<<nowx<<" "<<nowy<<endl;
cout<<(nowx+edx)<<" "<<nowy+edy<<endl;
}
cout<<edx<<" "<<edy<<endl;
}
}
signed main(){
init();
ios_base::sync_with_stdio(false), cin.tie(0);
cout<<fixed<<setprecision(12);
int t=1;
cin>>t;
while(t--){
solve();
}
return 0;
}
L.Candy Machine
题目分析
给定一个序列,每次可以选择一个区间,该区间的权值定义为严格大于区间平均数的数字个数,求最大的区间权值。
对输入序列排序然后左起扩区间,二分数字个数取最大值即可。
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e6 + 10;
int a[N];
inline void solve(){
int n = 0, sum = 0, ans = 0; cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
sort(a + 1, a + 1 + n);
for(int i = 1; i <= n; i++){
sum += a[i];
int l = 1, r = i;
while(l <= r){
int mid = l + r >> 1;
if(a[mid] * i > sum) r = mid - 1;
else l = mid + 1;
}
ans = max(ans, i - r);
}
cout << ans << endl;
}
signed main(){
ios_base::sync_with_stdio(false);
solve();
return 0;
}
M.BpbBppbpBB
题目分析
要求根据给定的形状找B字形和P字形,保证不存在重叠。
发现范围很小,于是考虑先 O ( n 2 ) O(n^2) O(n2)暴力枚举找出圆圈的数量,设为 c n t _ w cnt\_w cnt_w,找出 ′ # ′ '\#' ′#′的个数,设为 c n t _ b cnt\_b cnt_b;
然后设答案为 x x x个B字形, y y y个P字形,可以列出方程:
146 x + 100 y = c n t _ b 2 x + y = c n t _ w 146x + 100y = cnt\_b \\ 2x + y = cnt\_w 146x+100y=cnt_b2x+y=cnt_w
然后解方程即可。
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e3 + 10;
int n, m;
char g[N][N];
char sm[7][10] = {
"######",
"##..##",
"#....#",
"#....#",
"##..##",
"######"
};
inline bool dfs(int x, int y){
for(int i = 0; i < 6; i++){
for(int j = 0; j < 6; j++){
if(g[x + i][y + j] != sm[i][j]) return false;
}
}
return true;
}
inline void solve(){
cin >> n >> m;
int cnt_b = 0, cnt_w = 0;
for(int i = 1; i <= n; i++) cin >> g[i] + 1;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
if(g[i][j] == '#') cnt_b++;
if(dfs(i, j)) cnt_w++;
}
}
cout << (100 * cnt_w - cnt_b) / 54 << " " << (cnt_b - (73 * cnt_w)) / 27;
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
solve();
return 0;
}
边栏推荐
- 微信论坛交流小程序系统毕业设计毕设(6)开题答辩PPT
- JMeter interface automated test read case, execute and write back result
- kubernetes的简单化数据存储StorageClass(建立和删除以及初步使用)
- PMP项目管理考试过关口诀-1
- Gbu1510-asemi power supply special 15A rectifier bridge gbu1510
- 小程序多种开发方式对比-跨端?低代码?原生?还是云开发?
- Wechat forum exchange applet system graduation design (5) assignment
- 成年人只有一份主业是要付出代价的,被人事劝退后,我哭了一整晚
- Brush question 5
- opencv scalar传入三个参数只能显示黑白灰问题解决
猜你喜欢

Microbial health network, how to restore microbial communities

成年人只有一份主业是要付出代价的,被人事劝退后,我哭了一整晚
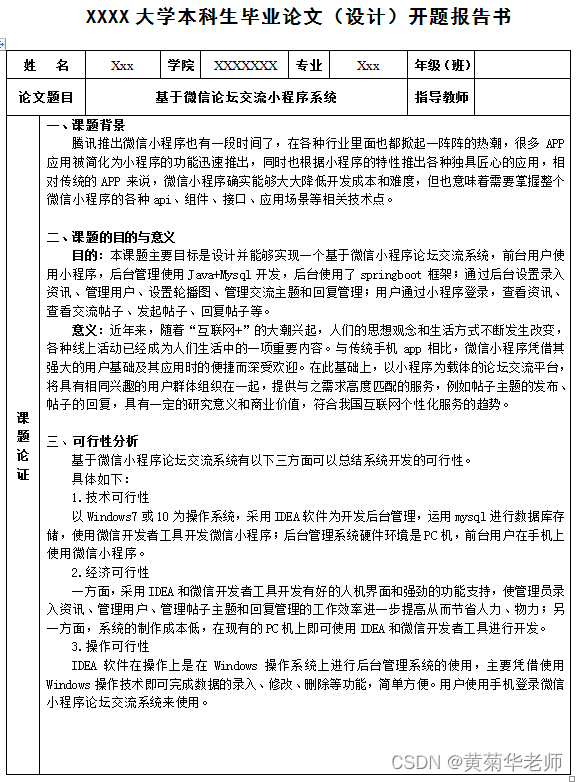
Wechat forum exchange applet system graduation design completion (4) opening report

微信论坛交流小程序系统毕业设计毕设(4)开题报告

微信论坛交流小程序系统毕业设计毕设(7)中期检查报告
When copying something from the USB flash disk, an error volume error is reported. Please run CHKDSK
Interview questions: how to test app performance?

Wechat forum exchange applet system graduation design completion (1) development outline
USB(十五)2022-04-14
Unity and webgl love each other
随机推荐
Online interview, how to better express yourself? In this way, the passing rate will be increased by 50%~
今日创见|企业促进创新的5大关键要素
小程序多种开发方式对比-跨端?低代码?原生?还是云开发?
嵌入式音频开发中的两种曲线
网络安全-钓鱼
Network security -burpsuit
Two kinds of curves in embedded audio development
[network] Introduction to C language
648. 单词替换
PCL . VTK files and Mutual conversion of PCD
Wechat forum exchange applet system graduation design (3) background function
Locate to the bottom [easy to understand]
Network security - Eternal Blue
十四、数据库的导出和导入的两种方法
Bit operation
Some parameters of Haikang IPC
Software evaluation center ▏ what are the basic processes and precautions for automated testing?
微信论坛交流小程序系统毕业设计毕设(4)开题报告
Talk about the design and implementation logic of payment process
网络安全-对操作系统进行信息查询