当前位置:网站首页>[Linear Algebra 03] Elimination method display and 4 solutions of AX=b
[Linear Algebra 03] Elimination method display and 4 solutions of AX=b
2022-08-04 21:32:00 【Moonfish and the Fourteen Lines】
This is still the caseMIT课程的笔记总结.First, the elimination method is displayed,The emphasis is realized from the matrixAThe process of reducing it to the simplest form,然后分类讨论AX = bin different ranksrsolution below.
Elimination method display
Still start with an example,已知矩阵A为:
A = [ 1 2 3 4 5 6 ] A = \begin{bmatrix} 1 &2 & 3 \\ 4 & 5 & 6 \end{bmatrix} A=[142536]
第一部分AX =0
Let's consider the equation first A X = 0 AX =0 AX=0 的解的情况,Apply elementary row transformations:
A = [ 1 2 3 4 5 6 ] ⇒ [ 1 2 3 0 − 3 − 6 ] ⇒ [ 1 2 3 0 1 2 ] ⇒ [ 1 0 − 1 0 1 2 ] = R A = \begin{bmatrix} 1 &2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \Rightarrow \begin{bmatrix} 1 &2 & 3 \\ 0 & -3 & -6 \end{bmatrix} \Rightarrow \begin{bmatrix} 1 &2 & 3 \\ 0 &1 & 2\end{bmatrix} \Rightarrow \begin{bmatrix} 1 &0 & -1 \\ 0 & 1 & 2 \end{bmatrix} =R A=[142536]⇒[102−33−6]⇒[102132]⇒[1001−12]=R
We are doing the simplest formRThe identity matrix can be found in the matrix I I I,and the rest can be recorded as F F F.关注 A X = 0 AX=0 AX=0,It is not difficult for us to find such a result, x 1 x_1 x1和 x 2 x_2 x2is the row where the main column is located(也即 I I I)the corresponding unknown,而 x 3 x_3 x3是自由变量,对应着 F F F.If the following notation is used
X ( p i v o t ) = [ x 1 x 2 ] X ( f r e e ) = [ x 3 ] X(pivot) = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \ \ \ X(free) = \begin{bmatrix} x_3 \end{bmatrix} X(pivot)=[x1x2] X(free)=[x3]
那么,对应 A X = 0 AX=0 AX=0The equation can be written:
[ I F ] [ X ( p i v o t ) X ( f r e e ) ] = I X ( p i v o t ) + F X ( f r e e ) = 0 \begin{bmatrix} I & F \end{bmatrix} \begin{bmatrix} X(pivot) \\ X(free) \end{bmatrix} =IX(pivot)+FX(free)=0 [IF][X(pivot)X(free)]=IX(pivot)+FX(free)=0
移项后就有:
X ( p i v o t ) = − F X ( f r e e ) X(pivot)=-FX(free) X(pivot)=−FX(free)
This is a very elegant formula in my opinion,That is to say, the solution of the original equation should have the following form:
x 1 = x 3 x 2 = − 2 x 3 x_1 = x_3 \\ x_2 = -2x_3 x1=x3x2=−2x3
在matlab中用rref函数就得到Gauss-Jordan Simplified row echelon matrix under elimination(reduced row echelon form).
>> A = [1,2,3;4,5,6];
>> rref(A)
ans =
1 0 -1
0 1 2
也可以用solveThe function verifies the correctness of the solution.
>> syms x1;syms x2; syms x3;
>> result = solve([x1+2*x2+3*x3,4*x1+5*x2+6*x3]); % result作为struct存在
>> result.x1
ans =
x3
>> result.x2
ans =
-2*x3
第二部分AX =b
Let's consider it further A X = b AX=b AX=b的情况,不如假设b列就为7和8,于是我们考虑A的增广矩阵,并Apply elementary row transformations,即
[ 1 2 3 ∣ 7 4 5 6 ∣ 8 ] ⇒ [ 1 2 3 ∣ 7 0 − 3 − 6 ∣ − 20 ] ⇒ [ 1 2 3 ∣ 7 0 1 2 ∣ 20 / 3 ] ⇒ [ 1 0 − 1 ∣ − 19 / 3 0 1 2 ∣ 20 / 3 ] \begin{bmatrix} 1 &2 & 3 & | & 7 \\ 4 & 5 & 6 & | & 8\end{bmatrix} \Rightarrow \begin{bmatrix} 1 &2 & 3 & | & 7 \\ 0 & -3 & -6 & | & -20\end{bmatrix} \Rightarrow \begin{bmatrix} 1 &2 & 3 & | & 7 \\ 0 & 1 & 2 & | & 20/3\end{bmatrix} \Rightarrow \begin{bmatrix} 1 &0 & -1 & | & -19/3 \\ 0 & 1 & 2 & | & 20/3\end{bmatrix} [142536∣∣78]⇒[102−33−6∣∣7−20]⇒[102132∣∣720/3]⇒[1001−12∣∣−19/320/3]
So there is a solution
x 1 = x 3 − 19 / 3 x 2 = − 2 x 3 + 20 / 3 x_1 = x_3-19/3 \\ x_2 = -2x_3+20/3 x1=x3−19/3x2=−2x3+20/3
同样可以用solvefunction to verify its correctness
>> syms x1;syms x2; syms x3;
>> result = solve([x1+2*x2+3*x3-7,4*x1+5*x2+6*x3-8]); % Modify the solution equation
>> result.x1
ans =
x3 - 19/3
>> result.x2
ans =
20/3 - 2*x3
Solution discussion
According to the example shown by the elimination method,我们已经对Gauss-Jordan The elimination method to solve the equation has a shallow understanding,Next we discuss the general solution case,即 A X = b AX = b AX=b in different ranksrsolution below,其中A是一个 m × n m\times n m×n The general matrix of .在matlab中,用rankfunction to find the rank of the matrix.
>> A = [1,2,3;4,5,6];
>> rank(A)
ans =
2
第1种情况:r = m < n
在这种情况下,The number of equations is less than the number of unknowns,There must be infinite solutions.And at this time because the rank of the matrix is r,So the number of free vectors is n-r,That is to say, the solution space should be a dimension of n-r的超平面.Take the example shown above as an example,It can be drawn that the solution space at this time is an in3维空间中的1维直线,The diagram and code are shown below: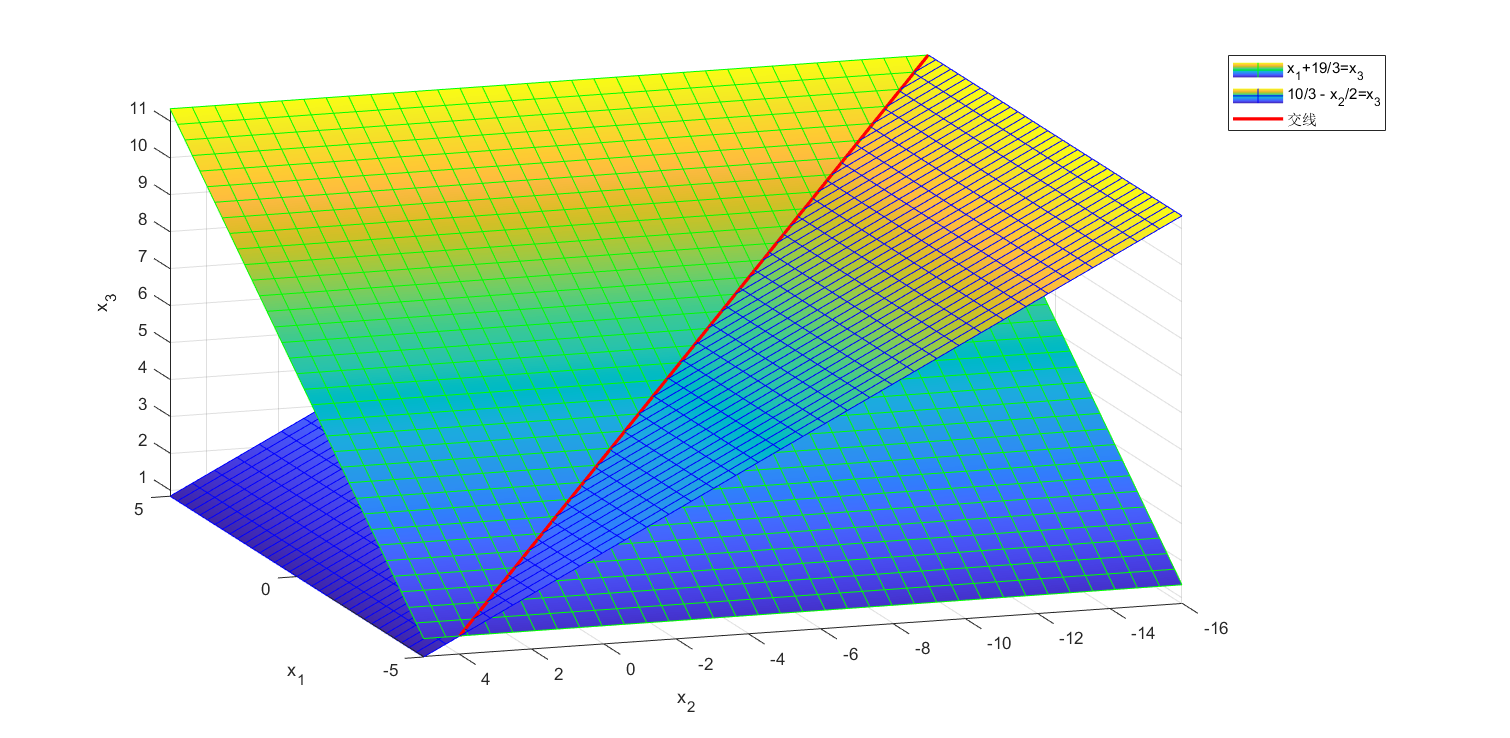
% 解空间为n-r的超平面
% 定义
syms x1; syms x2;
y1 = x1+19/3; y2 = 10/3-0.0000001*x1-0.5*x2; % Avoid default willx2读成x1
% fsurf画平面
fsurf(y1,EdgeColor='g'); hold on; fsurf(y2,EdgeColor='b');
% draw line of intersection
hold on;
fplot3(x1,-2*x1-6,x1+19/3,Color = 'r',Linewidth = 2)
% 标注
legend('x_1+19/3=x_3','10/3 - x_2/2=x_3','交线');
xlabel('x_1'); ylabel('x_2');zlabel('x_3');
第2种情况:r = n < m
实际上,再取AThe transposition can be studied
A T = [ 1 4 2 5 3 6 ] ⇒ [ 1 4 0 − 3 0 − 6 ] ⇒ [ 1 0 0 1 0 0 ] = [ I 0 ] = R A^{T} = \begin{bmatrix} 1 &4 \\ 2 & 5 \\ 3 & 6 \end{bmatrix} \Rightarrow \begin{bmatrix} 1 &4 \\ 0 & -3 \\ 0 & -6 \end{bmatrix} \Rightarrow \begin{bmatrix} 1 &0 \\ 0 & 1 \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} I \\ 0 \end{bmatrix} =R AT=⎣⎡123456⎦⎤⇒⎣⎡1004−3−6⎦⎤⇒⎣⎡100010⎦⎤=[I0]=R
此时可以发现,Look from the line, R R RThe upper part is the unit matrix I I I,下部为0矩阵. At this time, the number of equations is more than the number of unknowns,For the right end result itembLily made a request,That is, either satisfies as A T A^T AT各列的线性组合,得到一个特解;Either no solution .For example for the following equation,There is a special solution [ 1 , 1 ] T [1,1 ]^T [1,1]T:
x 1 + 4 x 2 = 5 2 x 1 + 5 x 2 = 7 3 x 2 + 6 x 3 = 9 x_1+4x_2 = 5 \\ 2x_1 + 5x_2 = 7 \\ 3x_2+6x_3 = 9 x1+4x2=52x1+5x2=73x2+6x3=9
换言之,此时bColumns are only in A T A^{T} ATA vector in the column space where it is located will have a solution.此例中,The request made is equivalent to bcolumn to be located3维空间中 A T A^T ATon the two-dimensional plane.A corresponding diagram can also be drawn,图和代码如下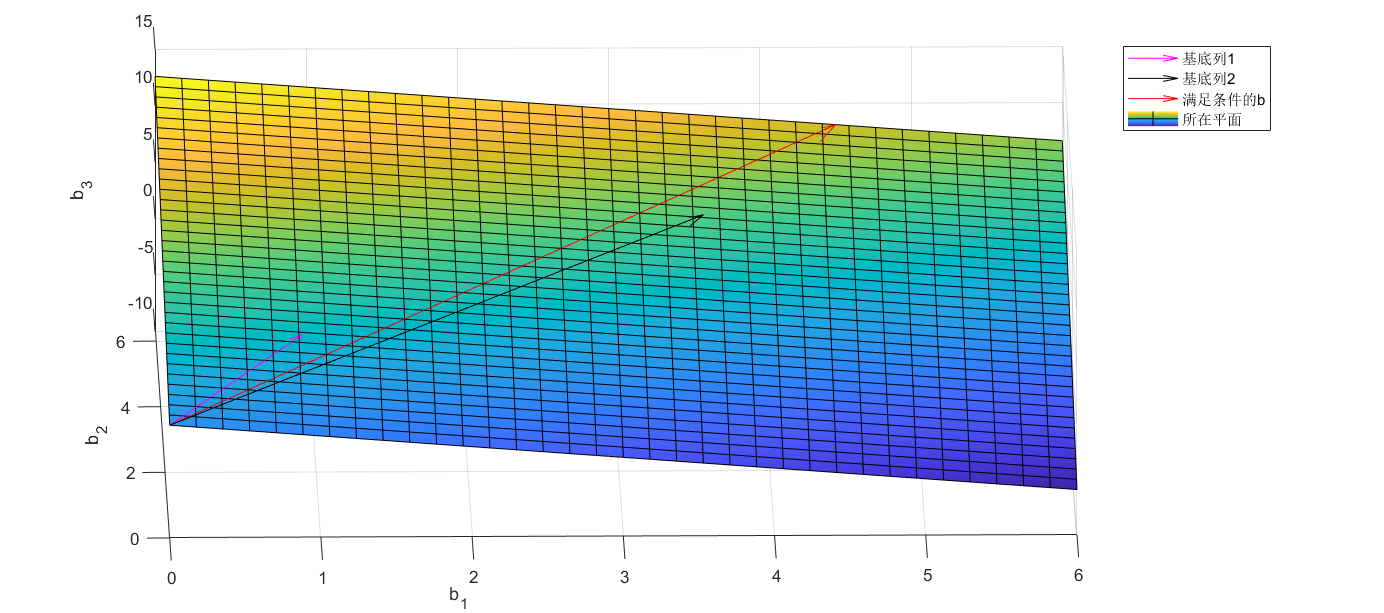
% bThe plane on which the column is located
% 画向量图
quiver3(0,0,0,1,2,3,'m'); hold on; quiver3(0,0,0,4,5,6,'black'); % 基底
hold on; quiver3(0,0,0,5,7,9,'r'); % 满足条件的b
V1 = [1;2;3]; V2 = [4;5;6];
% 求法向量
Vn = cross(V1,V2);
% 画平面
syms x1;syms x2;syms x3;
plane = -(x1*Vn(1)+x2*Vn(2))/Vn(3);
hold on;
fsurf(plane);
% 标注
legend('Basal column1','Basal column2','满足条件的b','所在平面');
xlabel('b_1'); ylabel('b_2'); zlabel('b_3');
第3种情况:r = n = m
直观地看,This will be the common part of the first two cases,So when the number of unknowns is equal to the number of equations,There will be one and only one solution.We can derive the general form of the solution,由于 r = n = m r = n = m r=n=m,Therefore, the square matrix is invertible at this time.Multiply both sides of the equation to the leftA的逆:
A X = b ⇒ A − 1 A X = A − 1 b ⇒ I X = A − 1 b ⇒ X = A − 1 b AX=b \Rightarrow A^{-1}AX=A^{-1}b \Rightarrow IX=A^{-1}b \Rightarrow X=A^{-1}b AX=b⇒A−1AX=A−1b⇒IX=A−1b⇒X=A−1b
于是就有The form of solution is A − 1 b A^{-1}b A−1b,and know this time R R RIt is equivalent to the unit matrix I I I.也举一个例子
B = [ 1 2 3 4 ] b = [ 5 6 ] B = \begin{bmatrix} 1 &2 \\ 3 & 4 \end{bmatrix} \ \ \ \ b= \begin{bmatrix} 5 \\ 6 \end{bmatrix} B=[1324] b=[56]
则计算结果为
X = B − 1 b = [ − 2 1 1.5 − 0.5 ] [ 5 6 ] = [ − 4 4.5 ] X = B^{-1}b= \begin{bmatrix} -2 & 1 \\ 1.5 &-0.5\end{bmatrix} \begin{bmatrix} 5 \\ 6 \end{bmatrix}= \begin{bmatrix} -4 \\ 4.5 \end{bmatrix} X=B−1b=[−21.51−0.5][56]=[−44.5]
用solvefunction to verify correctness:
>> syms x1; syms x2;
>> result = solve([x1+2*x2-5,3*x1+4*x2-6]);
>> ans1 = result.x1,ans2 = result.x2
ans1 =
-4
ans2 =
9/2
第4种情况:r < m,r < n
This shows that there are linearly dependent terms for both columns and rows,由前面的推导,我们容易得知,此时的RThe matrix should have the following form:
R = [ I F 0 0 ] R = \begin{bmatrix} I &F \\ 0 & 0 \end{bmatrix} R=[I0F0]
当 b = 0 b=0 b=0时一定有解0,而当 b ≠ 0 b \ne 0 b=0needs to be satisfiedbThe columns should be in the same column space as the matrix.
[ I F 0 0 ] [ X ( p i v o t ) X ( f r e e ) ] = [ X ( p i v o t ) + F X ( f r e e ) 0 ] \begin{bmatrix} I &F \\ 0 & 0 \end{bmatrix} \begin{bmatrix} X(pivot) \\ X(free) \end{bmatrix} = \begin{bmatrix} X(pivot) +FX(free) \\ 0 \end{bmatrix} [I0F0][X(pivot)X(free)]=[X(pivot)+FX(free)0]
即此时需要满足b的 m m m行中有 m − r m-r m−rLines are the rest r r rWhen a linear combination of rows is used,There will be a solution,且有无穷多解;Otherwise there will be no solution.Of course, the expression of the conditional judgment of whether there is a solution is the same as the first2种情况中,需要bThe representation that the column is in the column space of the matrix is equivalent.
For example, modify the matrixBand the corresponding columnb为
B = [ 1 2 2 4 ] b = [ 3 6 ] B = \begin{bmatrix} 1 &2 \\ 2 & 4 \end{bmatrix} \ \ \ \ b= \begin{bmatrix} 3 \\ 6 \end{bmatrix} B=[1224] b=[36]
There is a solution at this point,And the solution can be [ 1 , 1 ] T [1,1 ]^T [1,1]T, [ 3 , 0 ] T [3,0 ]^T [3,0]T, [ 0 , 1.5 ] T [0,1.5 ]^T [0,1.5]T等等,对bThe request made can be recorded as being in a two-dimensional plane1A one-dimensional straight line b 2 = 2 b 1 b_2=2b_1 b2=2b1,The solution space needs to be satisfied x 2 = − 0.5 x 1 + 1.5 x_2=-0.5x_1+1.5 x2=−0.5x1+1.5,It is easy to find that these two spaces are exactly perpendicular to each other.The corresponding picture display and code are as follows:
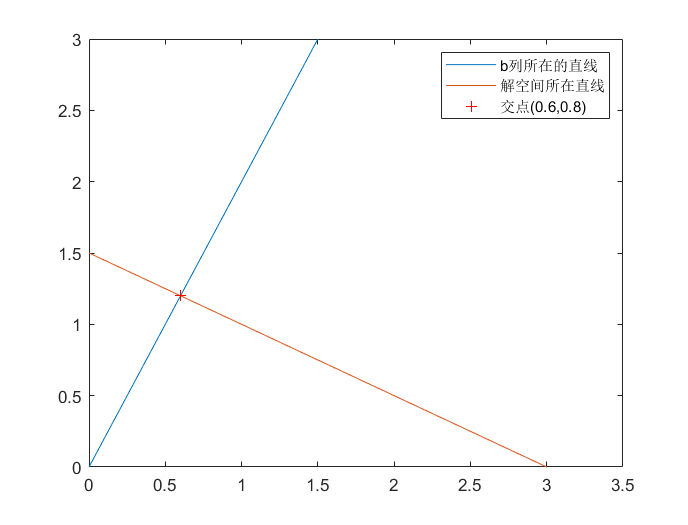
% solution space and bThe space where the column is located
syms x1;
% bThe line where the column is located
fplot(2*x1);
% The straight line where the solution space is located
hold on;
fplot(-x1/2+1.5);
% 标注
xlim([0,3.5]); ylim([0,3]);
% 求交点
hold on;
plot(0.6,1.2,'r+');
legend('bThe line where the column is located','The straight line where the solution space is located','交点(0.6,0.8)');
最后,Use a table to comb the number of comprehensions.
| 秩 r | 解的个数 |
|---|---|
| r = m < n | 无穷多解 |
| r = n < m | 0解或1解 |
| r = n = m | 1解 |
| r < m,r < n | 0solution or infinitely many solutions |
边栏推荐
- [2022 Hangzhou Electric Multi-School 5 1003 Slipper] Multiple Super Source Points + Shortest Path
- matlab drawing
- PyTorch Geometric (PyG) 安装教程
- 基于 Milvus 和 ResNet50 的图像搜索(部署及应用)
- 【ubuntu20.04安装MySQL以及MySQL-workbench可视化工具】
- 路由中的meta、params传参的一些问题(可传不可传,为空,搭配,点击传递多次参数报错)
- SPSS-System Clustering Software Practice
- [2022 Hangzhou Electric Power Multi-School 5 1012 Questions Buy Figurines] Application of STL
- 【2022杭电多校5 1012题 Buy Figurines】STL的运用
- How to solve the problem that the alarm information cannot be transmitted after EasyGBS is connected to the latest version of Hikvision camera?
猜你喜欢

2022年江苏省大学生电子设计竞赛(TI杯)B题 飞机 省级一等奖记录 “一个摆烂人的独白”

ES6高级-async的用法

PowerCLi 导入License到vCenter 7
强网杯2022——WEB
mdk5.14 cannot be burned
【uiautomation】微信好友列表获取(存储到txt中)
Red team kill-free development practice of simulated confrontation
PRIMAL: Pathfinding via Reinforcement and Imitation Multi-Agent Learning 代码解析
unity2D横版游戏教程9-对话框dialog
Yolov7:Trainable bag-of-freebies sets new state-of-the-art for real-time objectdetectors
随机推荐
mdk5.14 cannot be burned
PCBA方案设计——厨房语音秤芯片方案
经验分享|盘点企业进行知识管理时的困惑类型
模拟对抗之红队免杀开发实践
数电快速入门(四)(组合逻辑电路的分析以及设计的介绍)
基于 Milvus 和 ResNet50 的图像搜索(部署及应用)
proe和creo的区别有哪些
[2022 Nioke Duo School 5 A Question Don't Starve] DP
Common methods of js's new Function()
2022年江苏省大学生电子设计竞赛(TI杯)B题 飞机 省级一等奖记录 “一个摆烂人的独白”
LocalDate时间日期包的用法
拼多多开放平台订单信息查询接口【pdd.order.basic.list.get订单基础信息列表查询接口(根据成交时间)】代码对接教程
buu web
win10 uwp 使用 WinDbg 调试
搬走地下空间开发利用“绊脚石” 中地数码取得地下空间透明化技术突破
如何一键重装Win11系统 一键重装系统方法
js data type, throttling/anti-shake, click event delegation optimization, transition animation
Go----Go 语言基础之标识符、关键字、命名规范、变量、常量
PowerCLi 批量配置NTP
LayaBox---TypeScript---Example