Ml backward propagation

neural network

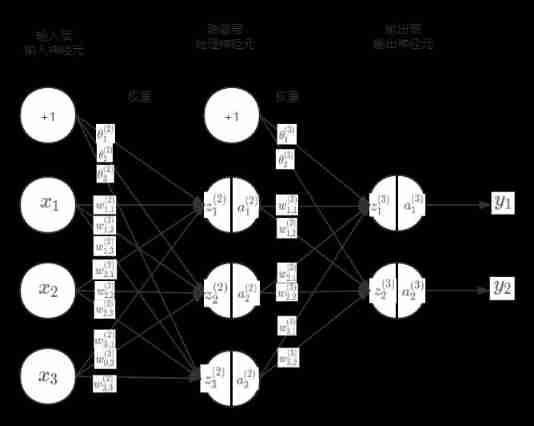
Introduce

• $a_n^{(l)}$：l（layer） The layer number ,n（number） Number , The number of neurons
• $w_{i,j}^{(l)}$：$i=OnOnelayergodtheelementEdNumber=a_n^{(l)}Ofn$,$j=NextOnelayergodtheelementEdNumber=a_n^{(l+1)}Ofn$
• $w_{i,j}^{(l)}$：i,j Represents the position of this element in the matrix ,i On behalf of the line ,j Representative column
• $$w^{(2)}=\left(\begin{array}{ccc}{w}_{1,1}^{(2)}& w_{1,2}^{(2)}& w_{1,3}^{(2)}\\ w_{2,1}^{(2)}& w_{2,2}^{(2)}& w_{2,3}^{(2)}\\ w_{3,1}^{(2)}& w_{3,2}^{(2)}& w_{3,3}^{(2)}\end{array}\right)$$
• $$w^{(3)}=\left(\begin{array}{cc}{w}_{1,1}^{(3)}& w_{1,2}^{(3)}\\ w_{2,1}^{(3)}& w_{2,2}^{(3)}\\ w_{3,1}^{(3)}& w_{3,2}^{(3)}\end{array}\right)$$
• $a_n^{(l)}=g(z_n^{(l)})$g yes sigmoid function
• $x_n=a_n^{(1)}$
• ${\theta }_1^{(2)}=w_{0,1}^{(2)},{\theta }_2^{(2)}=w_{0,2}^{(2)},{\theta }_3^{(2)}=w_{0,3}^{(2)},{\theta }_1^{(3)}=w_{0,1}^{(3)},{\theta }_2^{(3)}=w_{0,2}^{(3)}$

Arithmetic representation ：

• $a_1^{(2)}=g(z_1^{(2)})=g({\theta }_1^{(2)}\ast 1+w_{1,1}^{(2)}{x}_1+w_{2,1}^{(2)}{x}_2+w_{3,1}^{(2)}{x}_3)$
• $a_2^{(2)}=g(z_2^{(2)})=g({\theta }_2^{(2)}\ast 1+w_{1,2}^{(2)}{x}_1+w_{2,2}^{(2)}{x}_2+w_{3,2}^{(2)}{x}_3)$
• $a_3^{(2)}=g(z_3^{(2)})=g({\theta }_3^{(2)}\ast 1+w_{1,3}^{(2)}{x}_1+w_{2,3}^{(2)}{x}_2+w_{3,3}^{(2)}{x}_3)$
• $a_1^{(3)}=g(z_1^{(3)})=g({\theta }_1^{(3)}\ast 1+w_{1,1}^{(3)}{x}_1+w_{2,1}^{(3)}{x}_2+w_{3,1}^{(3)}{x}_3)$
• $a_2^{(3)}=g(z_2^{(3)})=g({\theta }_2^{(3)}\ast 1+w_{1,2}^{(3)}{x}_1+w_{2,2}^{(3)}{x}_2+w_{3,2}^{(3)}{x}_3)$
• $a_1^{(3)}=y_1$
• $a_2^{(3)}=y_2$

The matrix represents ：

• $z^{(l)}=w^{(l)}{a}^{(l-1)}+{\theta }^{(l)}$, Weight of this layer * The output of the upper layer + The weight of the offset

Forward propagation

Definition

• Input 》 Handle 》 Output , Take the output of the previous layer as the input of the next layer

It is known that

• $x^{(l)}$ and $y$
• Using forward propagation, we can find ：$z^{(l)},a^{(l)}=g(z^{(l)})$

Back propagation

Introduce

• Backward propagation or reverse propagation is Backward propagation of loss
• MLP Is the loss back propagation and optimization method （ gradient descent ） combination
• Back propagation calculates the gradient of weight in the loss function of neural network , The random gradient descent algorithm uses this gradient for learning
• Machine learning requires computation $w$( The weight ), After defining the loss function , Calculate the loss function $w$( The weight ) Gradient of , The gradient descent algorithm uses this gradient for learning （ to update $w$）

Determine the loss function ：

• Mean square error （MSE）：$C(w,\theta )=\frac{1}{2}||a^{(L)}-y|{|}_2^2=\frac{1}{2}\sum _{i=1}^n(a_i-y_i{)}^2$,C yes cost（ Cost loss ）,L（layer） Said the last 1 layer ,$a^{(L)}$ Is the output layer vector ,$y$ Is the real output vector , $||x|{|}_2$ Is a two norm , That's the distance.

Calculate the loss function $w$( The weight ) Gradient of ：
One ： Calculate the output layer In the loss function $w$( The weight ) Gradient of

• $$\begin{array}{rl}\frac{\partial C(w,\theta )}{\partial w^{(L)}}& =\frac{\partial C(w,\theta )}{\partial a^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial z^{(L)}}{\partial w^{(L)}}\\ & =(a^{(L)}-y)\odot g(z^{(L)}{)}^{{}^{\prime }}{a}^{(L-1)}\end{array}$$
• $$\begin{array}{rl}\frac{\partial C(w,\theta )}{\partial {\theta }^{(L)}}& =\frac{\partial C(w,\theta )}{\partial a^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial z^{(L)}}{\partial {\theta }^{(L)}}\\ & =(a^{(L)}-y)\odot g(z^{(L)}{)}^{{}^{\prime }}\end{array}$$
• $\odot$ yes Hadamaji Hadamard Product, The matrix is multiplied by the corresponding position elements

Two ： Count the penultimate 2 layer In the loss function $w$( The weight ) Gradient of

• $$\begin{array}{rl}\frac{\partial C(w,\theta )}{\partial w^{(L-1)}}& =\frac{\partial C(w,\theta )}{\partial a^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial z^{(L)}}{\partial a^{(L-1)}}\frac{\partial a^{(L-1)}}{\partial z^{(L-1)}}\frac{\partial z^{(L-1)}}{\partial w^{(L-1)}}\\ & =(a^{(L)}-y)\odot g(z^{(L)}{)}^{{}^{\prime }}\odot w^{(L)}g(z^{(L-1)}{)}^{{}^{\prime }}{a}^{(L-2)}\end{array}$$
• $$\begin{array}{rl}\frac{\partial C(w,\theta )}{\partial {\theta }^{(L-1)}}& =\frac{\partial C(w,\theta )}{\partial a^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial z^{(L)}}{\partial a^{(L-1)}}\frac{\partial a^{(L-1)}}{\partial z^{(L-1)}}\frac{\partial z^{(L-1)}}{\partial {\theta }^{(L-1)}}\\ & =(a^{(L)}-y)\odot g(z^{(L)}{)}^{{}^{\prime }}\odot w^{(L)}g(z^{(L-1)}{)}^{{}^{\prime }}\end{array}$$
• $\frac{\partial C(w,\theta )}{\partial {\theta }^{(L)}}$ And $\frac{\partial C(w,\theta )}{\partial w^{(L-1)}}$ The difference between 3 A formula

3、 ... and ： Draw out the public part of No. 1 and No. 2 middle school

• Make ${\delta }^{(L)}=\frac{\partial C(w,\theta )}{\partial z^{(L)}}=(a^{(L)}-y)\odot g(z^{(L)}{)}^{{}^{\prime }}$
• be ${\delta }^{(L-1)}=\frac{\partial C(w,\theta )}{\partial z^{(L-1)}}=(a^{(L)}-y)\odot g(z^{(L)}{)}^{{}^{\prime }}\odot w^{(L)}g(z^{(L-1)}{)}^{{}^{\prime }}$
• be ${\delta }^{(L-1)}={\delta }^{(L)}\odot w^{(L)}g(z^{(L-1)}{)}^{{}^{\prime }}$
• Then I know ${\delta }^{(L-1)}$ and ${\delta }^{(L)}$ The recurrence relation of

Four ： Calculate all layers In the loss function $w$( The weight ) Gradient of
The first L layer （ Output layer ） Loss function pair $w$( The weight ) Gradient of ：

• $\frac{\partial C(w,\theta )}{\partial w^{(L)}}={\delta }^{(L)}{a}^{(L-1)}$
• $\frac{\partial C(w,\theta )}{\partial {\theta }^{(L)}}={\delta }^{(L)}$

The first L-1 layer （ Output layer ） Loss function pair $w$( The weight ) Gradient of ：

• $\frac{\partial C(w,\theta )}{\partial w^{(L-1)}}={\delta }^{(L-1)}{a}^{(L-2)}={\delta }^{(L)}\odot w^{(L)}g(z^{(L-1)}{)}^{{}^{\prime }}{a}^{(L-2)}$
• $\frac{\partial C(w,\theta )}{\partial {\theta }^{(L-1)}}={\delta }^{(L-1)}={\delta }^{(L)}\odot w^{(L)}g(z^{(L-1)}{)}^{{}^{\prime }}$

The first $l$ Layer loss function pair $w$( The weight ) Gradient of ：

• $\frac{\partial C(w,\theta )}{\partial w^{(l)}}={\delta }^{(l)}{a}^{(l-1)}$
• $\frac{\partial C(w,\theta )}{\partial {\theta }^{(l)}}={\delta }^{(l)}$
• $\frac{\partial C(w,\theta )}{\partial w^{(l-1)}}={\delta }^{(l-1)}{a}^{(l-2)}={\delta }^{(l)}\odot w^{(l)}g(z^{(l-1)}{)}^{{}^{\prime }}{a}^{(l-2)}$
• $\frac{\partial C(w,\theta )}{\partial {\theta }^{(l-1)}}={\delta }^{(l-1)}={\delta }^{(l)}\odot w^{(l)}g(z^{(l-1)}{)}^{{}^{\prime }}$
• know ${\delta }^{(l)}$ You know $\frac{\partial C(w,\theta )}{\partial w^{(l)}}$ You know The first $l$ Layer loss function pair $w$( The weight ) Gradient of

5、 ... and ： summary
It is known that ：

• $x^{(l)}$ and $y$

Forward propagation can be found ：

• $z^{(l)},a^{(l)}=g(z^{(l)})$

Backward propagation can be found ：

• ${\delta }^{(L)}$： because ${\delta }^{(L)}=\frac{\partial C(w,\theta )}{\partial z^{(L)}}=(a^{(L)}-y)\odot g(z^{(L)}{)}^{{}^{\prime }}$ in $a^{(L)},y,g(z^{(L)})=a^{(L)}$ All known
• ${\delta }^{(L-1)}$： because ${\delta }^{(L-1)}={\delta }^{(L)}\odot w^{(L)}g(z^{(L-1)}{)}^{{}^{\prime }}$ in $w^{(L)},g(z^{(L-1)})$ All known ,==${\delta }^{(L)}$== It can be seen from the above that
• ${\delta }^{(L-2)}$： because ${\delta }^{(L-2)}={\delta }^{(L-1)}\odot w^{(L-1)}g(z^{(L-2)}{)}^{{}^{\prime }}$ in $w^{(L-1)},g(z^{(L-2)})$ All known ,==${\delta }^{(L-1)}$== It can be seen from the above that
• ${\delta }^{(l-1)}$： because ${\delta }^{(l-1)}={\delta }^{(l)}\odot w^{(l)}g(z^{(l-1)}{)}^{{}^{\prime }}$ in $w^{(l)},g(z^{(l-1)})$ All known ,==${\delta }^{(l)}$== It can be seen from the above that
• $\frac{\partial C(w,\theta )}{\partial w^{(L)}}={\delta }^{(L)}{a}^{(L-1)}$
• $\frac{\partial C(w,\theta )}{\partial {\theta }^{(L)}}={\delta }^{(L)}$
• $\frac{\partial C(w,\theta )}{\partial w^{(L-1)}}={\delta }^{(L-1)}{a}^{(L-2)}$
• $\frac{\partial C(w,\theta )}{\partial {\theta }^{(L-1)}}={\delta }^{(L-1)}$
• $\frac{\partial C(w,\theta )}{\partial w^{(L-2)}}={\delta }^{(L-2)}{a}^{(L-3)}$
• $\frac{\partial C(w,\theta )}{\partial {\theta }^{(L-2)}}={\delta }^{(L-1)}$
• $\frac{\partial C(w,\theta )}{\partial w^{(l)}}={\delta }^{(l)}{a}^{(l-1)}$
• $\frac{\partial C(w,\theta )}{\partial {\theta }^{(l)}}={\delta }^{(l)}$

summary

1. Clear purpose ： Calculate the weight $w$ And offset $\theta$（$y=ax+b,z=wx+\theta ,a=g(z)=g(wx+\theta )$）
2. initialization $w,\theta$
3. Forward propagation calculation $z^{(l)},a^{(l)}$
4. Define the loss function - Mean square error (MSE)$C(w,\theta )=\frac{1}{2}||a^{(L)}-y|{|}_2^2=\frac{1}{2}\sum _{i=1}^n(a_i-y_i{)}^2$
5. Calculate the output layer (L layer ) Of ${\delta }^{(L)}$

• • ${\delta }^{(L)}=\frac{\partial C(w,\theta )}{\partial z^{(L)}}=(a^{(L)}-y)\odot g(z^{(L)}{)}^{{}^{\prime }}$

6. Backward propagation calculation $l$ Layer of ${\delta }^{(l)},l=2,...,L-1$
7. Using machine learning methods - The gradient descent algorithm updates the weight $w$ And offset $\theta$

• • $w^{(l)}=w^{(l)}-\alpha \frac{\partial C(w,\theta )}{\partial w^{(l)}}$
• • ${\theta }^{(l)}={\theta }^{(l)}-\alpha \frac{\partial C(w,\theta )}{\partial {\theta }^{(l)}}$

8. if $w,\theta$ The change of is less than the given threshold （ Express $w,\theta$ No more changes ） Or the number of iterations , Exit iteration
9. Output $w,\theta$