当前位置:网站首页>leetcode-304:二维区域和检索 - 矩阵不可变
leetcode-304:二维区域和检索 - 矩阵不可变
2022-07-07 08:17:00 【菊头蝙蝠】
题目
给定一个二维矩阵 matrix,以下类型的多个请求:
- 计算其子矩形范围内元素的总和,该子矩阵的 左上角 为 (row1, col1) ,右下角 为 (row2, col2) 。
实现 NumMatrix 类:
- NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
- int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。
示例 1: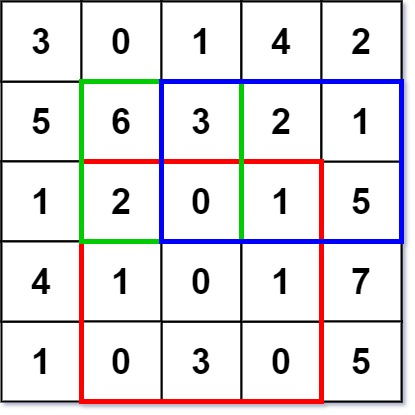
输入:
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出:
[null, 8, 11, 12]
解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)
解题
方法一:前缀和
preSums[i][j]表示左上角为(0,0),右下角索引为(i,j)的矩阵里的所有元素和
1、首先通过下述递推关系式计算出preSums[i][j]
S ( O , D ) = S ( O , C ) + S ( O , B ) − S ( O , A ) + D S(O,D)=S(O,C)+S(O,B)−S(O,A)+D S(O,D)=S(O,C)+S(O,B)−S(O,A)+D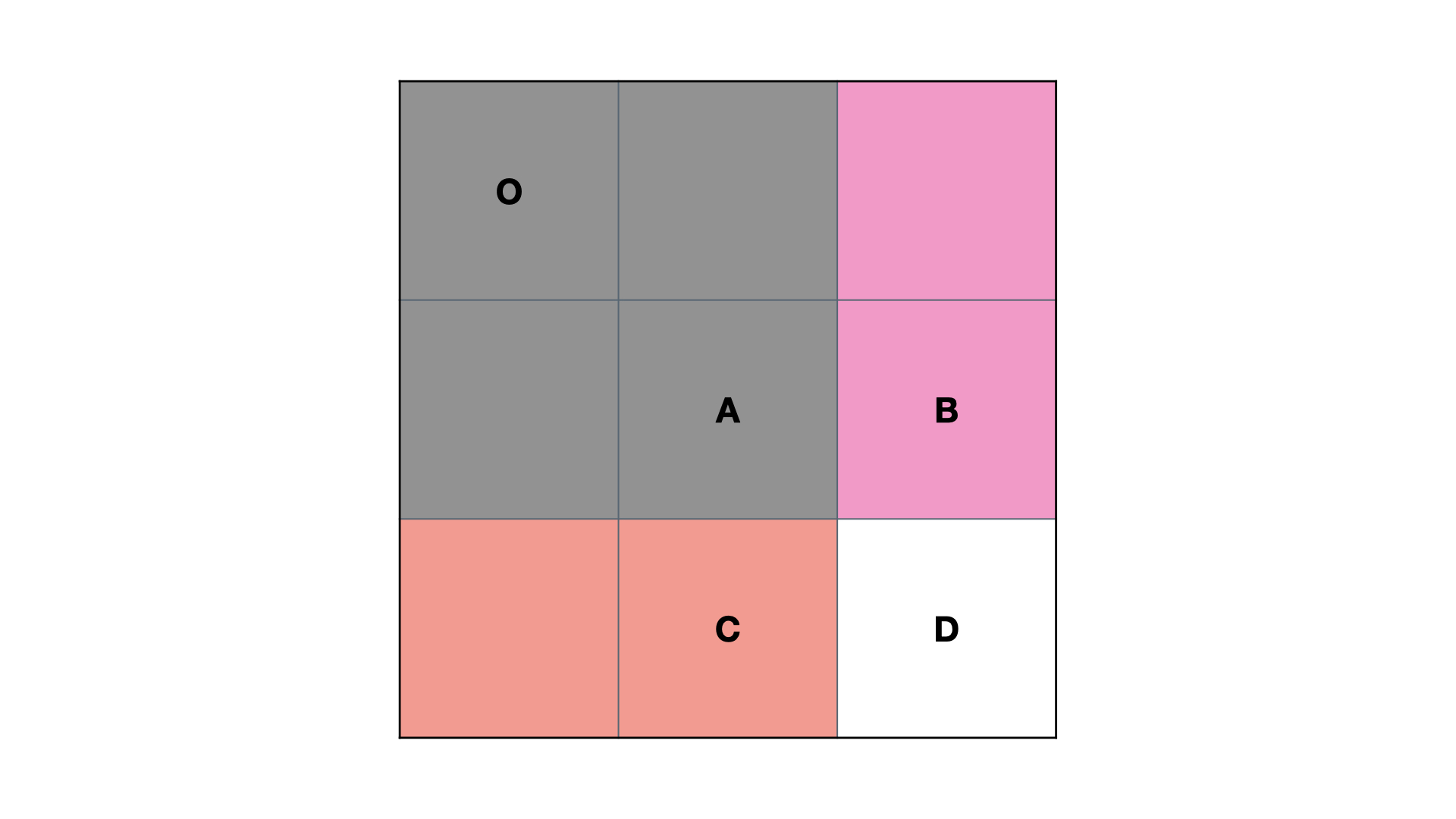
2、根据已经计算出的preSums,可以得出想要计算的矩阵中所有元素之和
S ( A , D ) = S ( O , D ) − S ( O , E ) − S ( O , F ) + S ( O , G ) S(A,D)=S(O,D)−S(O,E)−S(O,F)+S(O,G) S(A,D)=S(O,D)−S(O,E)−S(O,F)+S(O,G)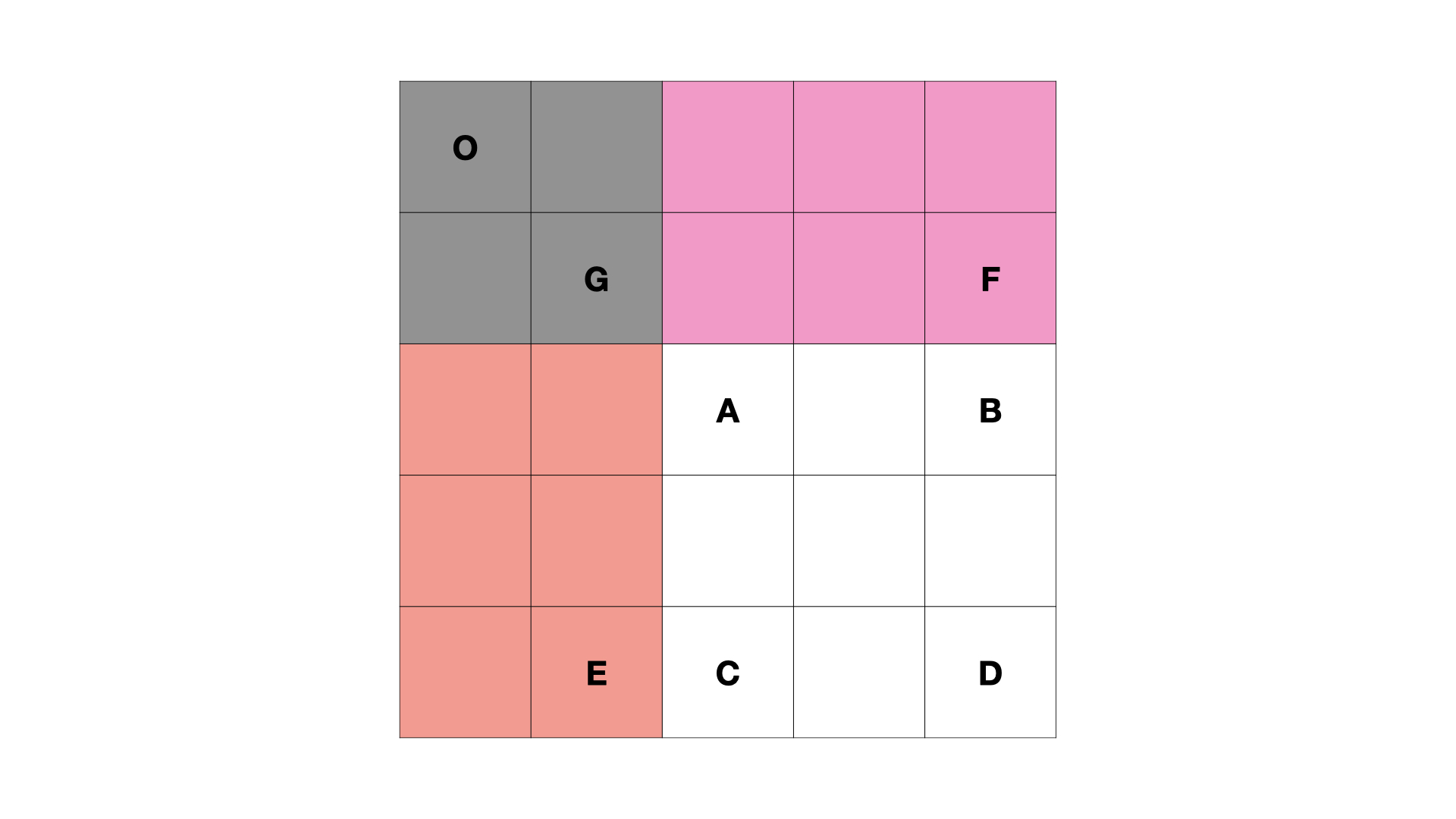
class NumMatrix {
public:
vector<vector<int>> preSums;
NumMatrix(vector<vector<int>>& matrix) {
int m=matrix.size();
int n=matrix[0].size();
preSums.resize(m+1,vector<int>(n+1));
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
preSums[i+1][j+1]=preSums[i+1][j]+preSums[i][j+1]-preSums[i][j]+matrix[i][j];
}
}
}
int sumRegion(int row1, int col1, int row2, int col2) {
return preSums[row2+1][col2+1]-preSums[row1][col2+1]-preSums[row2+1][col1]+preSums[row1][col1];
}
};
边栏推荐
- 【acwing】789. 数的范围(二分基础)
- Trajectory planning for multi-robot systems: Methods and applications 综述阅读笔记
- Some properties of leetcode139 Yang Hui triangle
- Kotlin实现微信界面切换(Fragment练习)
- Postman interface test IV
- LeetCode 练习——113. 路径总和 II
- Chris Lattner, père de llvm: Pourquoi reconstruire le logiciel d'infrastructure ai
- OpenGL glLightfv 函数的应用以及光源的相关知识
- Pdf document signature Guide
- 2022.7.5DAY597
猜你喜欢

Some properties of leetcode139 Yang Hui triangle
Pdf document signature Guide
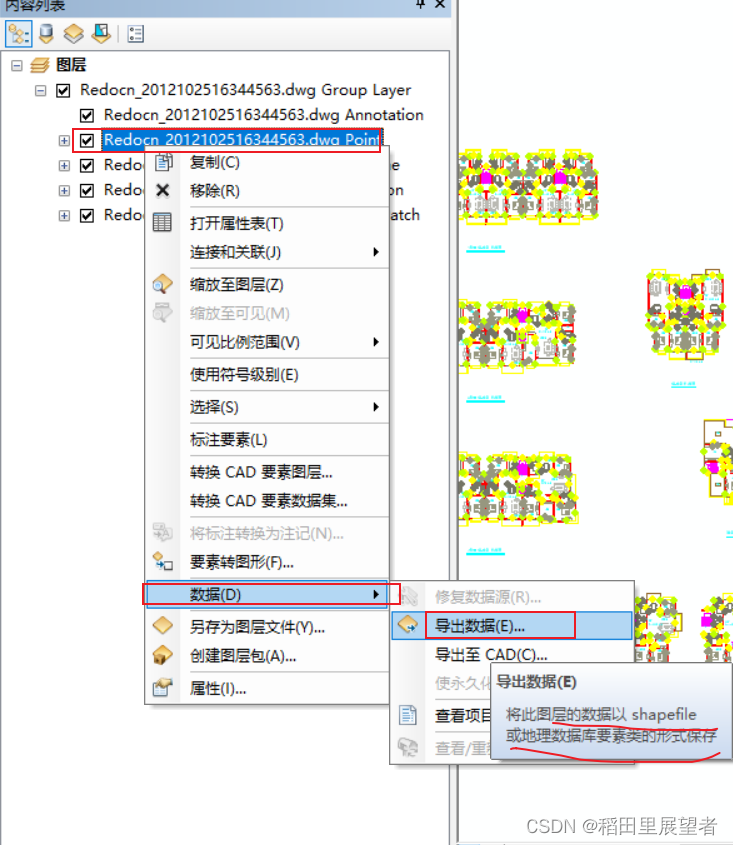
ArcGIS operation: converting DWG data to SHP data
![[second on] [jeecgboot] modify paging parameters](/img/59/55313e3e0cf6a1f7f6b03665e77789.png)
[second on] [jeecgboot] modify paging parameters
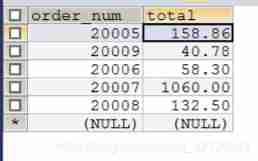
Use the fetch statement to obtain the repetition of the last row of cursor data

OpenGL glLightfv 函数的应用以及光源的相关知识
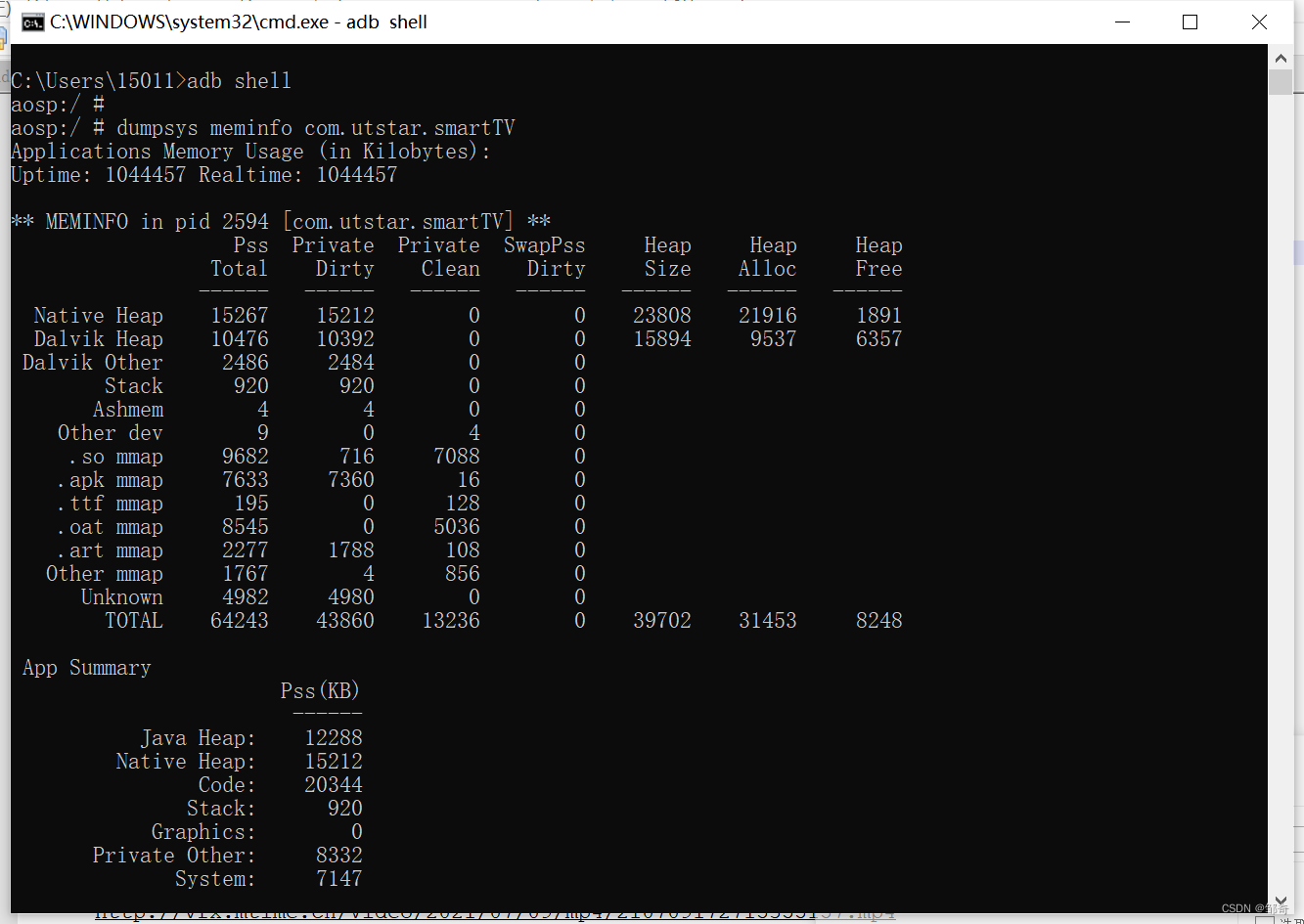
Adb 实用命令(网络包、日志、调优相关)
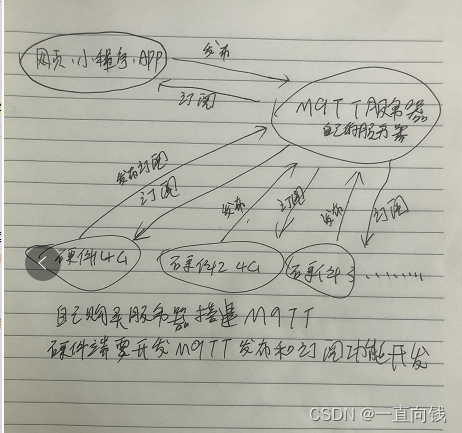
Several schemes of building hardware communication technology of Internet of things
![[ORM framework]](/img/72/13eef38fc14d85978f828584e689a0.png)
[ORM framework]

ISP、IAP、ICP、JTAG、SWD的编程特点
随机推荐
嵌入式工程师如何提高工作效率
Fiddler break point
Wallys/IPQ6010 (IPQ6018 FAMILY) EMBEDDED BOARD WITH ON-BOARD WIFI DUAL BAND DUAL CONCURRENT
Embedded background - chip
XML configuration file parsing and modeling
Smart city construction based on GIS 3D visualization technology
串口通讯继电器-modbus通信上位机调试软件工具项目开发案例
Inno Setup 打包及签名指南
Study summary of postgraduate entrance examination in August
Vs code specifies the extension installation location
A small problem of bit field and symbol expansion
BigDecimal数值比较
Can I open a stock trading account online? Is it safe
2022.7.3DAY595
Methods of adding centerlines and centerlines in SolidWorks drawings
Remote meter reading, switching on and off operation command
[牛客网刷题 Day5] JZ77 按之字形顺序打印二叉树
大整数类实现阶乘
基于gis三维可视化技术的智慧城市建设
Postman interface test I