当前位置:网站首页>AcWing 179. Factorial decomposition problem solution
AcWing 179. Factorial decomposition problem solution
2022-07-06 11:16:00 【Octopus loving monster】
AcWing 197. Factorial decomposition Answer key
List of articles
Title Description
Given integer N N N , Try factorial N ! N! N! Decomposing prime factor , According to the form of the basic theorem of arithmetic, output the p i p_i pi and c i c_i ci that will do
Input format
An integer N N N
Output format
N ! N! N! The result of decomposing the prime factor , There are several lines , Each row of a pair of p i , c i p_i,c_i pi,ci , Means to contain p i c I p_i^{c_I} picI term . according to p i p_i pi Sequential output from small to large
Data range
3 ≤ N ≤ 1 0 6 3 \le N \le 10^6 3≤N≤106
Answer key
about N ! N! N! The quality factor of , We can judge , The maximum quality factor does not exceed N N N
prove :
Through the basic theorem of arithmetic
For any positive integer, there are
x = p 1 α 1 ⋅ p 2 α 2 ⋅ p 3 α 3 … ⋅ p n α n x=p_1^{\alpha_1} · p_2^{\alpha_2}·p_3^{\alpha_3}\dots·p_n^{\alpha_n} x=p1α1⋅p2α2⋅p3α3…⋅pnαn
among P i P_i Pi by x x x The quality factor of
about 1 1 1 ~ N N N Each integer of can be decomposed into the form of basic theorem of arithmetic
therefore N ! N! N! The basic theorem of arithmetic is the former N N N The product of the basic arithmetic theorem of numbers , There is no more than N N N The quality factor of
Obtain evidence
So we just need to sift out 1 1 1~ N N N The prime number of
First, use the linear sieve to screen out the prime numbers
public static void init(int n)
{
Arrays.fill(isPrime,true);
for(int i=2;i<=n;i++)
{
if(isPrime[i])
Primes[cnt++]=i;
for(int j=0;j<cnt;j++)
{
int p=Primes[j];
if(p*i>n)
break;
isPrime[p*i]=false;
if(i%p==0)
break;
}
}
}
After sifting the prime number
We calculate the order of each prime
Computation 1 1 1 ~ N N N How many numbers in have prime numbers p p p
Easy to get N / P N/P N/P Numbers have prime numbers p, These numbers are p Multiple , So these numbers have factors p p p
According to N / P 2 N/P^2 N/P2 The number contains factors p 2 p^2 p2
By analogy , We can calculate when N / P k N/P^k N/Pk When is 0, Prime number P P P The corresponding maximum order is k k k
The code for calculating the order is as follows
for(int i=0;i<cnt;i++)
{
int res=0;
int p=Primes[i];
int tmp=n;
while(tmp>0)
{
res+=tmp/p;
tmp/=p;
}
System.out.println(Primes[i]+" "+res);
}
Complete code
import java.io.*;
import java.util.*;
public class Main{
static int n;
static final int N=(int)1e6+10;
static boolean[] isPrime=new boolean[N];
static int[] Primes=new int[N];
static int cnt=0;
public static void init(int n)
{
Arrays.fill(isPrime,true);
for(int i=2;i<=n;i++)
{
if(isPrime[i])
Primes[cnt++]=i;
for(int j=0;j<cnt;j++)
{
int p=Primes[j];
if(p*i>n)
break;
isPrime[p*i]=false;
if(i%p==0)
break;
}
}
}
public static void main(String[] agrs) throws IOException
{
BufferedReader reader=new BufferedReader(new InputStreamReader(System.in));
n=Integer.parseInt(reader.readLine());
init(n);
for(int i=0;i<cnt;i++)
{
int res=0;
int p=Primes[i];
int tmp=n;
while(tmp>0)
{
res+=tmp/p;
tmp/=p;
}
System.out.println(Primes[i]+" "+res);
}
}
}
边栏推荐
- 01项目需求分析 (点餐系统)
- Install MySQL for Ubuntu 20.04
- Csdn-nlp: difficulty level classification of blog posts based on skill tree and weak supervised learning (I)
- [recommended by bloggers] C MVC list realizes the function of adding, deleting, modifying, checking, importing and exporting curves (with source code)
- Remember a company interview question: merge ordered arrays
- Install mysql5.5 and mysql8.0 under windows at the same time
- Solve the problem that XML, YML and properties file configurations cannot be scanned
- Are you monitored by the company for sending resumes and logging in to job search websites? Deeply convinced that the product of "behavior awareness system ba" has not been retrieved on the official w
- MySQL other hosts cannot connect to the local database
- JDBC原理
猜你喜欢
【博主推荐】C# Winform定时发送邮箱(附源码)
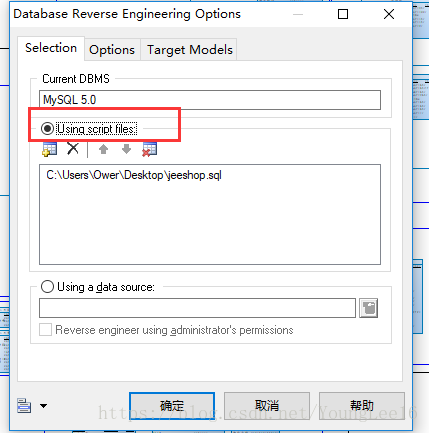
Navicat 導出錶生成PDM文件

一键提取pdf中的表格

Solution: log4j:warn please initialize the log4j system properly

【博主推荐】asp.net WebService 后台数据API JSON(附源码)
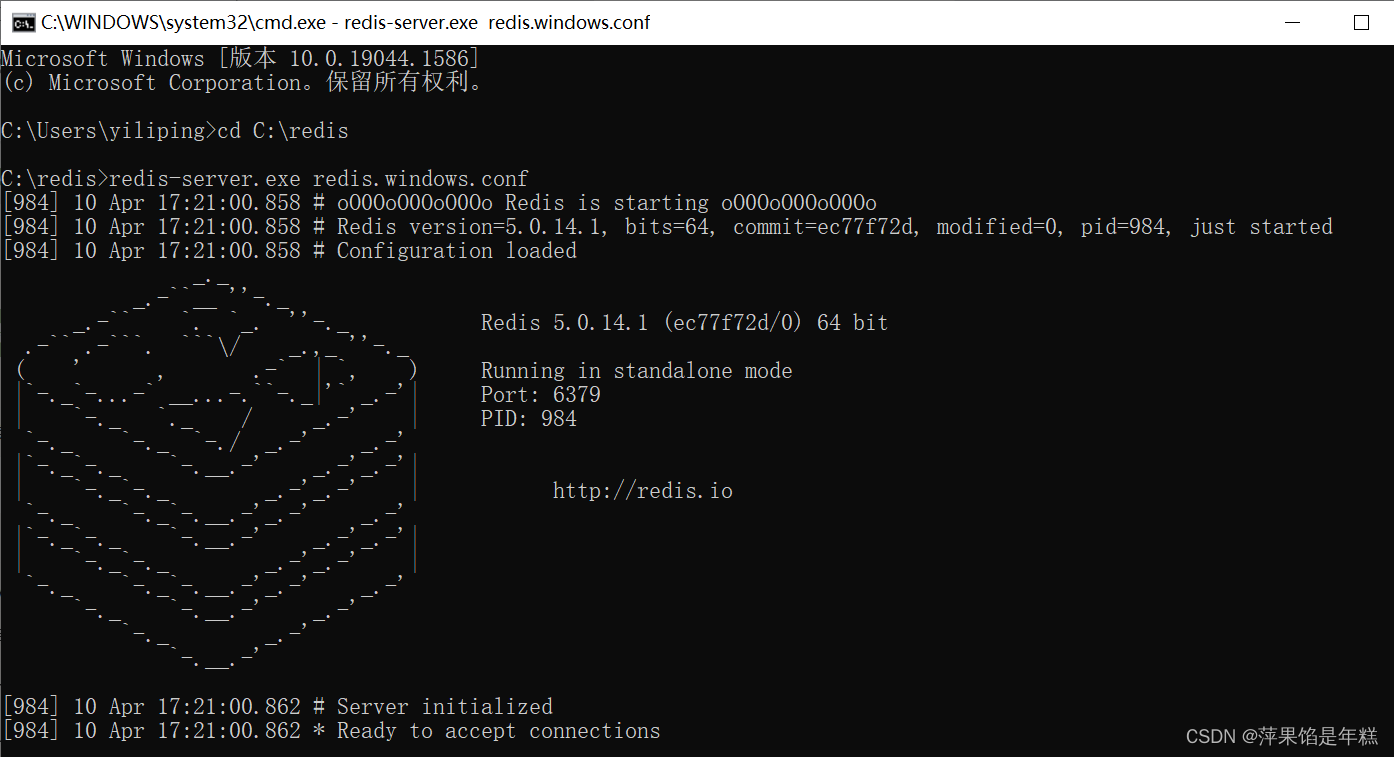
Windows下安装MongDB教程、Redis教程

Asp access Shaoxing tourism graduation design website
QT creator specifies dependencies
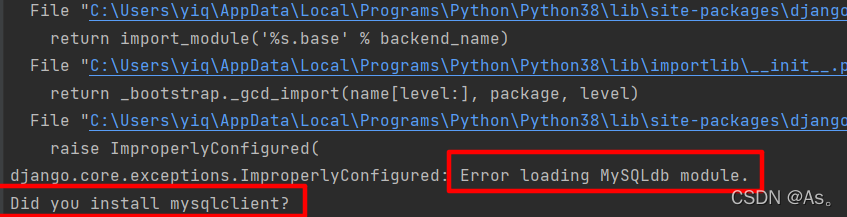
Django运行报错:Error loading MySQLdb module解决方法

Classes in C #
随机推荐
Navicat 導出錶生成PDM文件
++Implementation of I and i++
Solution: log4j:warn please initialize the log4j system properly
Ansible practical Series II_ Getting started with Playbook
【博主推荐】C#生成好看的二维码(附源码)
NPM an error NPM err code enoent NPM err syscall open
Windows下安装MongDB教程、Redis教程
CSDN question and answer module Title Recommendation task (II) -- effect optimization
Swagger、Yapi接口管理服务_SE
Csdn-nlp: difficulty level classification of blog posts based on skill tree and weak supervised learning (I)
MySQL完全卸载(Windows、Mac、Linux)
记一次某公司面试题:合并有序数组
02 staff information management after the actual project
QT creator uses Valgrind code analysis tool
Dotnet replaces asp Net core's underlying communication is the IPC Library of named pipes
Detailed reading of stereo r-cnn paper -- Experiment: detailed explanation and result analysis
Install MySQL for Ubuntu 20.04
Swagger, Yapi interface management service_ SE
When you open the browser, you will also open mango TV, Tiktok and other websites outside the home page
Error connecting to MySQL database: 2059 - authentication plugin 'caching_ sha2_ The solution of 'password'