当前位置:网站首页>[classical control theory] summary of automatic control experiment
[classical control theory] summary of automatic control experiment
2022-07-05 23:21:00 【robinbird_】
※ Automatic control system script writing
1、 Variable
sym, syms Symbolic variables
sym a; syms a b; f = str2sym('a+ b^2');
2、 Basic operation
Derivation
dfa = diff(f function ,a For which variable ( partial ) guide );Accumulated faintness
intb = int(f function ,b Which variable to integrate ,b1,b2 Section );Laplace transform
%t You still have to define it in advance ,s Finding Laplace transform will bring ft = exp(2*t); L1 = laplace(ft);Inverse Laplace transform
ftt = ilaplace(L1);
3、 Control system model
Polynomial form ( Transfer function model )
The coefficients are stored continuously in an array , An array of numerators and denominators , Pass from high to low
num = [1 2 3]; % The coefficient corresponding to the molecule den = [4 5 6 7]; % The coefficient corresponding to the denominator gs = tf(num,den);
Zero pole model
Two arrays are required , ditto , Add one more k gain
z = [1 2 3]'; % zero , Pay attention to add transpose p = [4 5 6 7]; % pole k = 9; gs2 = zpk(z,p,k);
Interconversion
[num,den] = zp2tf(z,p,k); % Zero pole transfer functionOther expressions
molecular / The denominator expression has zpk type , But need tf When the format , Use conv( It's polynomial multiplication ) Unified conversion to polynomial type , for example
num = [1 2.9 2]; den = conv([1 0],[1 10 25]); gs = tf(num,den); % The root locus diagram should be drawn later
4、 Connection of models
Series connection — series
[num3,den3] = series(num,den,num2,den2);parallel connection — parallel
[num3,den3] = parallel(num,den,num2,den2);feedback — feedback
[num3,den3] = feedback(numg,deng,numh,denh,sign); % First give G(s) Transmission characteristics of , Give again H(s) Transmission characteristics of , Last sign Is the default -1( Negative feedback ), It can be changed +1( The positive feedback )Unit feedback — cloop
[num3,den3] = cloop(numg,deng,sign); % Less than above H(s)
5、 Typical input function
Unit step function — step
t = [0:0.1:100]; num = 1; den = [1 0.4 1]; step(num, den, t); %t The main thing is to explain how long to draw t Of ct Images ,num,den Directly transfer the characteristic array of the closed-loop transfer functionUnit pulse function — impulse
t = [0:0.1:100]; num = 1; den = [1 0.4 1]; impulse(num, den, t); %t The main thing is to explain how long to draw t Of ct Images ,num,den Directly transfer the characteristic array of the closed-loop transfer functionCustom input — lsim
t = 0:0.1:10; %u Contain with t The expression of , such as u = t; % perhaps lsim(num,den,u,t); lsim(z,p,k,u,t); % It is still the beginning to give the characteristics of the closed-loop transfer function of the system , The above two forms are acceptable ,u It's input r(t), Contain with t Expression of integer ,t Is time % for example , This is used for frequency characteristic test , Input a sine function to the system t = [0:0.001:10]; rt = 1* sin(15 * t); lsim(nums,dens,rt,t);Be careful : After using all the above functions , If you use its return value , It defaults to direct single window drawing ; If you use a variable to store the return value ( It is the result of the system output , It's a one-dimensional array ), Then it can be used to draw multiple graphs
6、3 A system characteristic image
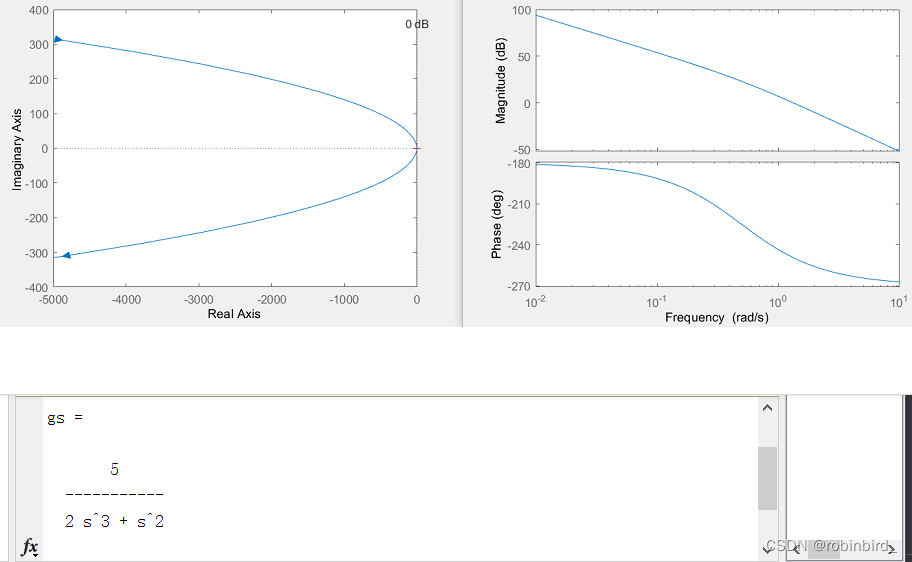
Root locus drawing
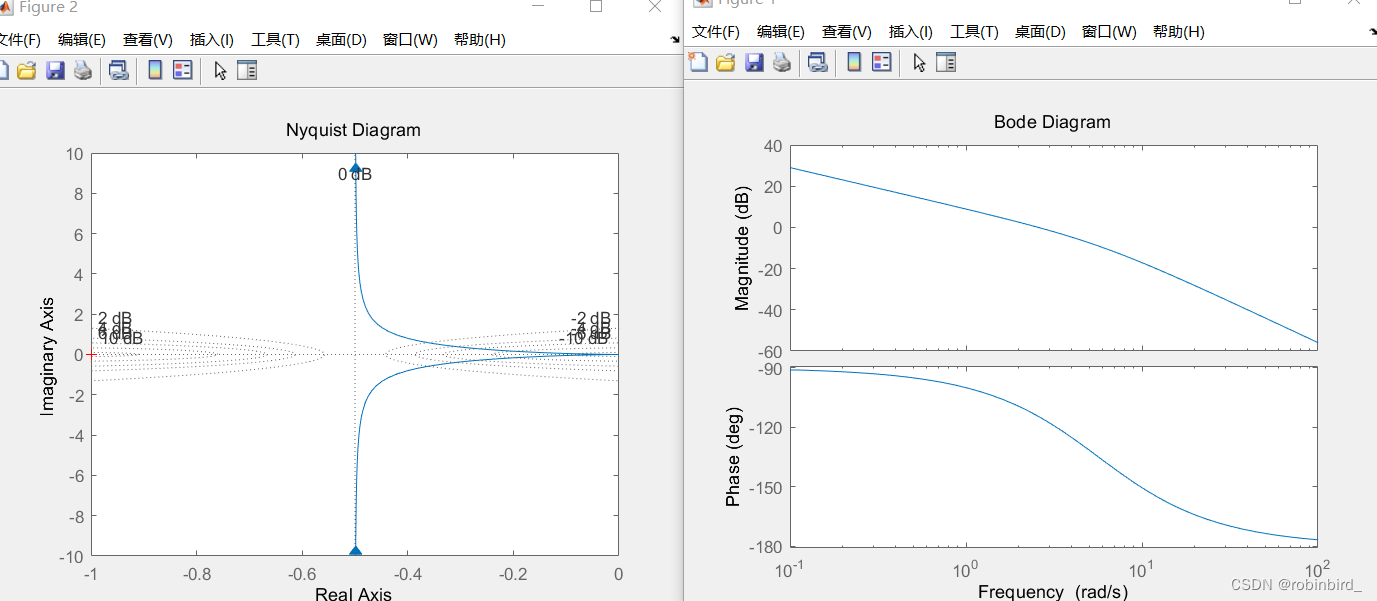
gs = tf(num,den); rlocus(gs); % What is given is the complete function expression , And here the first expression of the open-loop transmittal ( Without root track gain K*)Nyquist
matlab The painting contains w from 0 To -∞ Track of , Completely symmetrical with the positive part , Never mind
nyquist(gs); % Pass reference pass Open loop transmittal expressionbode chart
bode(gs); % Same as before , Generally, it draws an open-loop logarithmic amplitude frequency diagram , Then give the expression of open loopfor example , Left root locus , Right bode chart
7、matlab Drawing method
Basic drawing settings
grid; % Adding grid xlabel(" Title name "); % Set the name of the abscissa ylabel(" ditto "); % Vertical axis name title("abb"); % The name of the drawn imageMultigraph drawing
(1) Draw a picture in one window , Be careful ,grid and legend Such special requirements do not apply to all windows , Every figure Add it separately if necessary
figure; %code, Draw a picture figure; %code, Draw another picture , And so on % give an example , First draw a bode chart , Draw another Nyquist diagram figure; z = [-0.2]; p = [0 -0.1 -4]; k = 16; [num,den] = zp2tf([],[0 -4*sqrt(2)],k); tf_gs = tf(num,den); bode(tf_gs); figure; nyquist(tf_gs); grid; %attention
(2) Multiple graphs are drawn in one window
First of all, we need not let matlab Draw the response directly , Just use variables to receive the return value
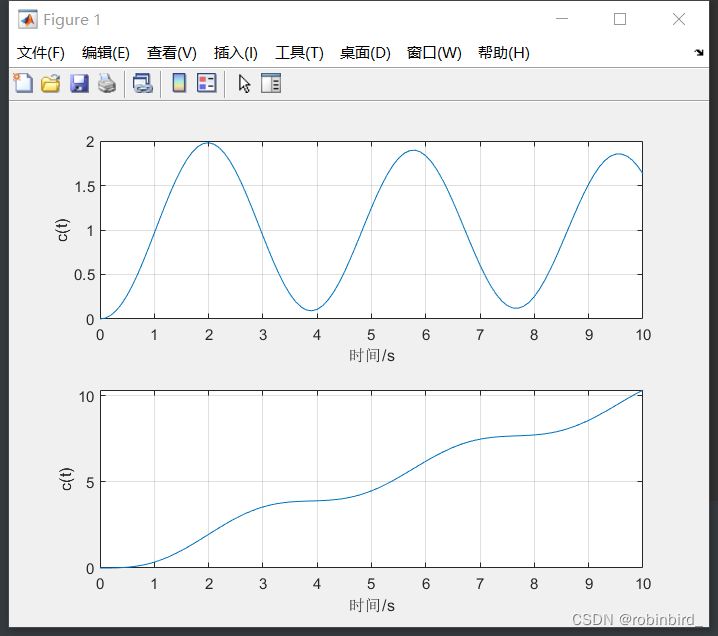
t = 0:0.1:10; y_step = step(numfi,denfi,t); % Receive return value u = t; y_ramp = lsim(numfi,denfi,u,t); % Receive return value Then use a format similar to the previous one ,subplot Refer to this article for the parameters of :http://t.csdn.cn/pXIZ5
subplot(x1,y1,z1); plot(t1,c1); axis normal; subplot(x2,y2,z2); plot(t2,c2); axis normal; % give an example , Continue with the previous content subplot(2,1,1); plot(t,y_step); xlabel(" Time /s"); ylabel("c(t)"); grid; axis normal subplot(2,1,2); plot(t,y_ramp); xlabel(" Time /s"); ylabel("c(t)"); axis normal grid;
※simulink Plug in emulation
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-WYEGSDxt-1657012369295)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220421104137653.png)]](/img/e5/8b609ccabbd25ebe5fbada29686760.png)
Name of common component library
And here is , Directly check the corresponding... In the component library name Search and you'll get
gain K gain
Transfer function
Polynomial type transfer fcn:
Zero pole model Zero-Pole
Oscilloscope scope
Ramp signal ramp
Step signal step
Sine signal sine wave
Sum up sum
Dead zone module dead zone
Limiting module saturation
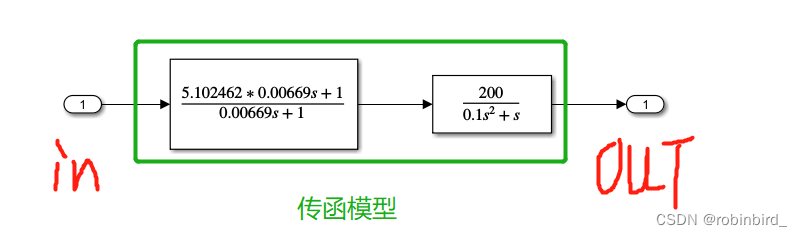
Analysis of system characteristic diagram of transfer function
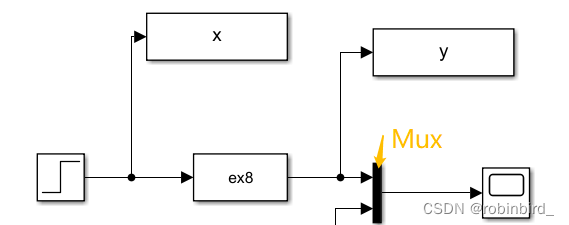
First use of in and out modular , Build the following model
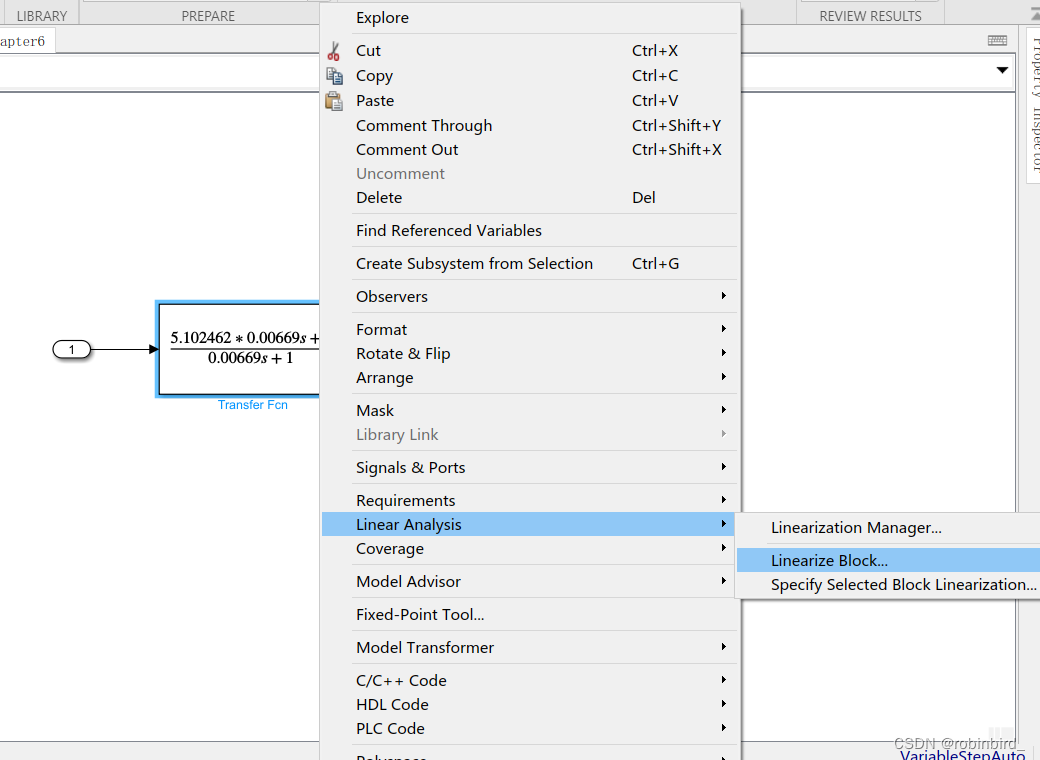
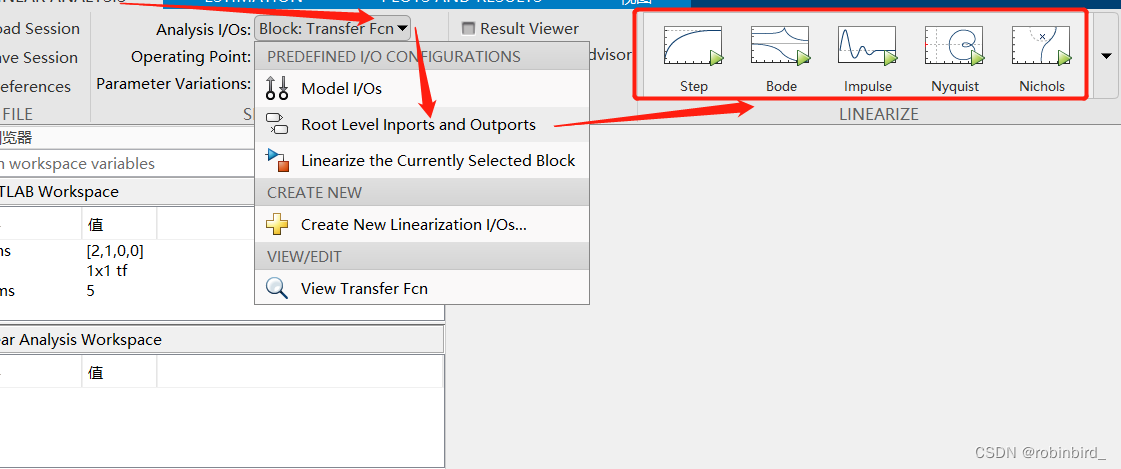
For a transmittal module , Right click , find Linearize block
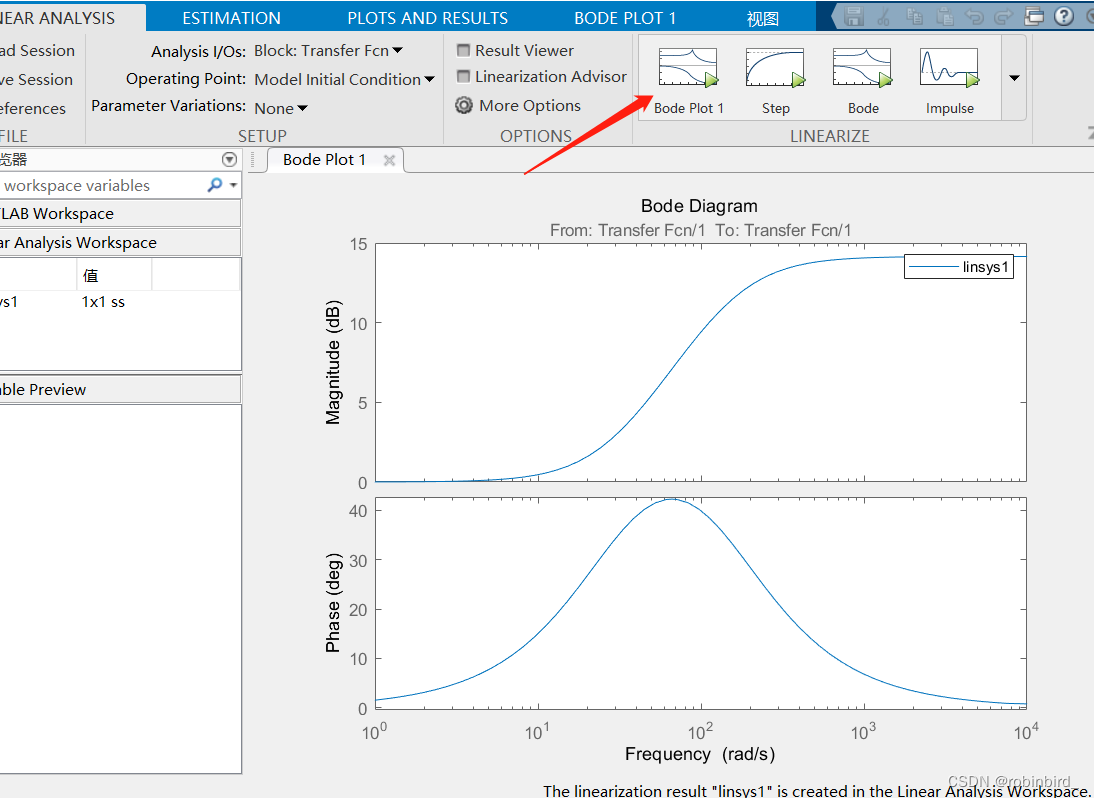
Select the source of input and output as shown in the following figure , Then click the system characteristic curve you want to obtain , You can draw directly
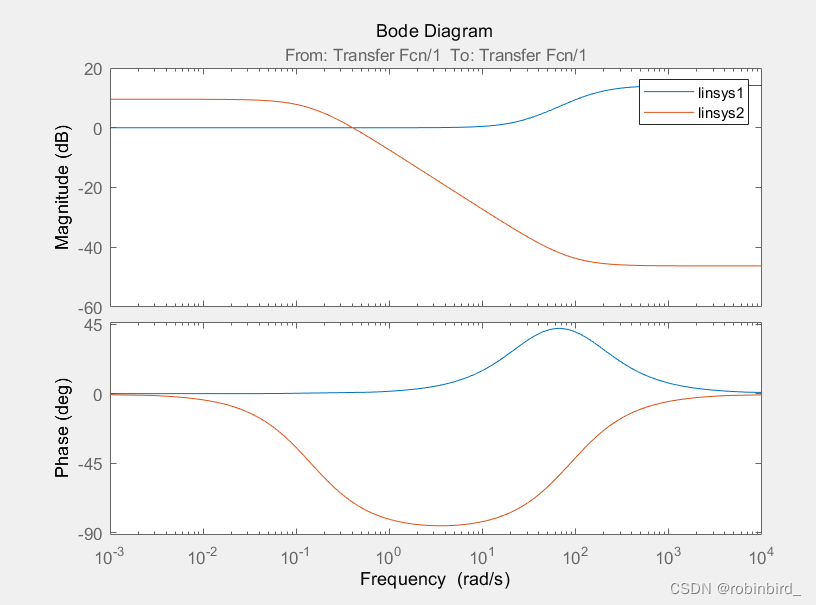
If you want to draw multiple curves on the same graph ( It is mostly used for system calibration ), Just after the first drawing ,( I'm right simulink After simply modifying the parameter value of the model ), Then click the current plot The button , There are two pictures , Stack in this way
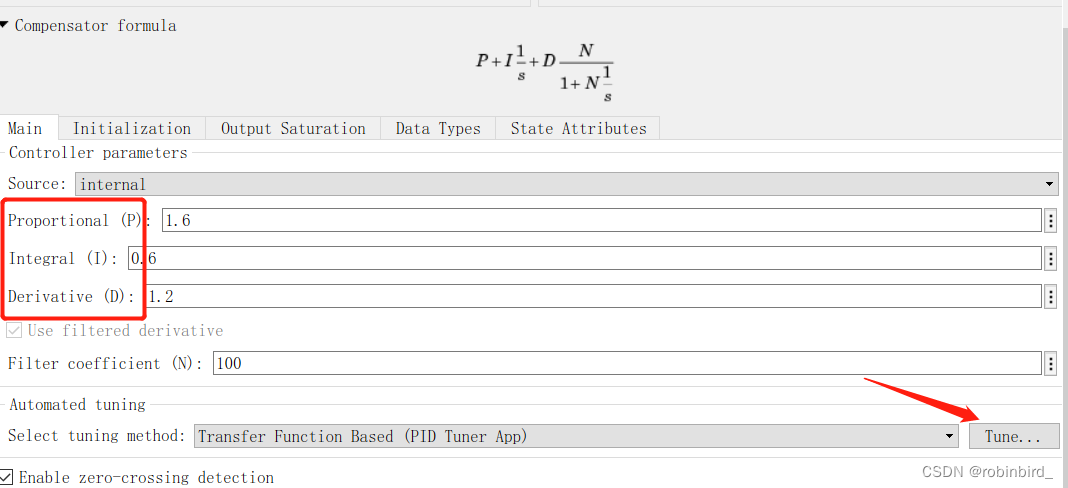
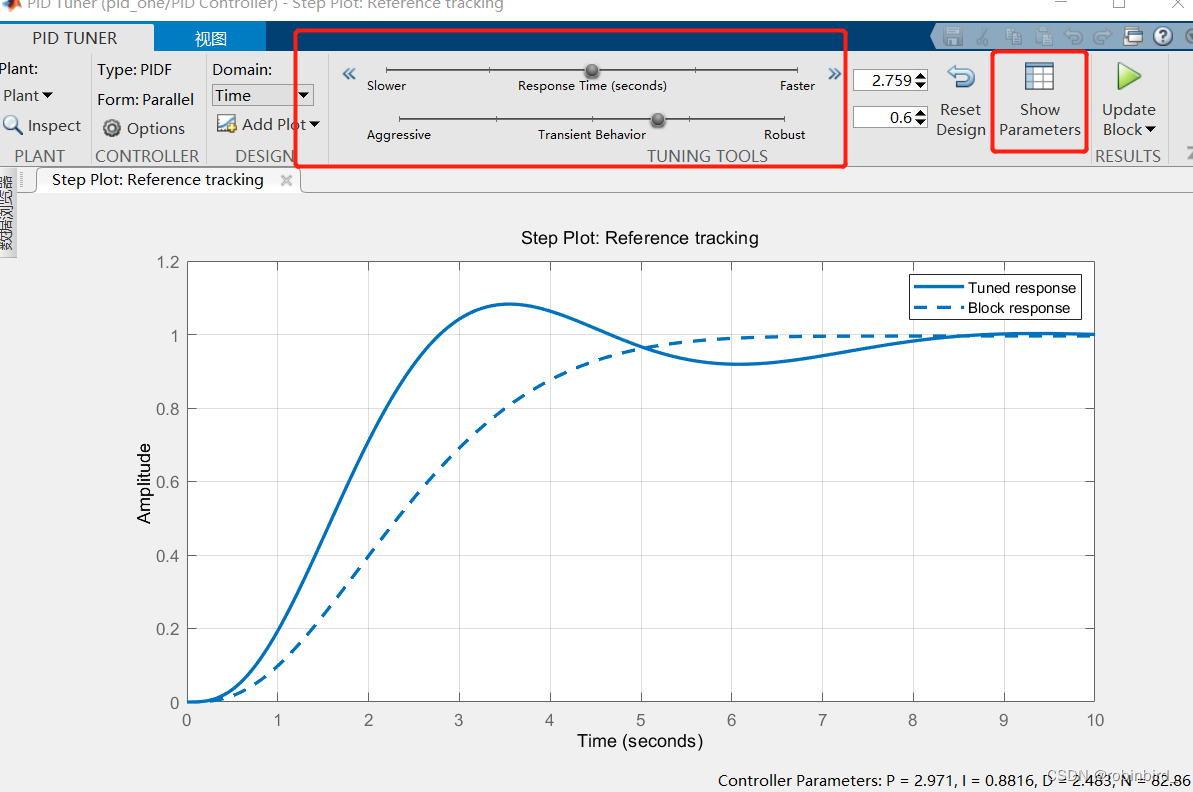
PID modular PID controller
Corresponding modification PID Three parameters are sufficient
You can also use PID tunner Instantly adjust rapidity and volatility , See the picture below
※ Scripts and simulink Dream linkage
take simulink Simulation data is used .m Script processing
Directly use the transfer function model , Through one more simout To transmit the data is
Several setting modes
structure with time
This is Time And corresponding Output
plot(out.so.time, out.so.signals.values); %out It should be added so to simout The name of life , This can be customized , Because a .slx There can be many songs simout modular
structure
Only Output
yt = out.so.signals.values;array
Only Output , Return... As an array
plot(out.so);timeseries
plot(out.so.Time,out.so.Data);use .m Draw Lissajou figure / Time domain response curve
Here we directly use the code of the eighth experiment of automatic control
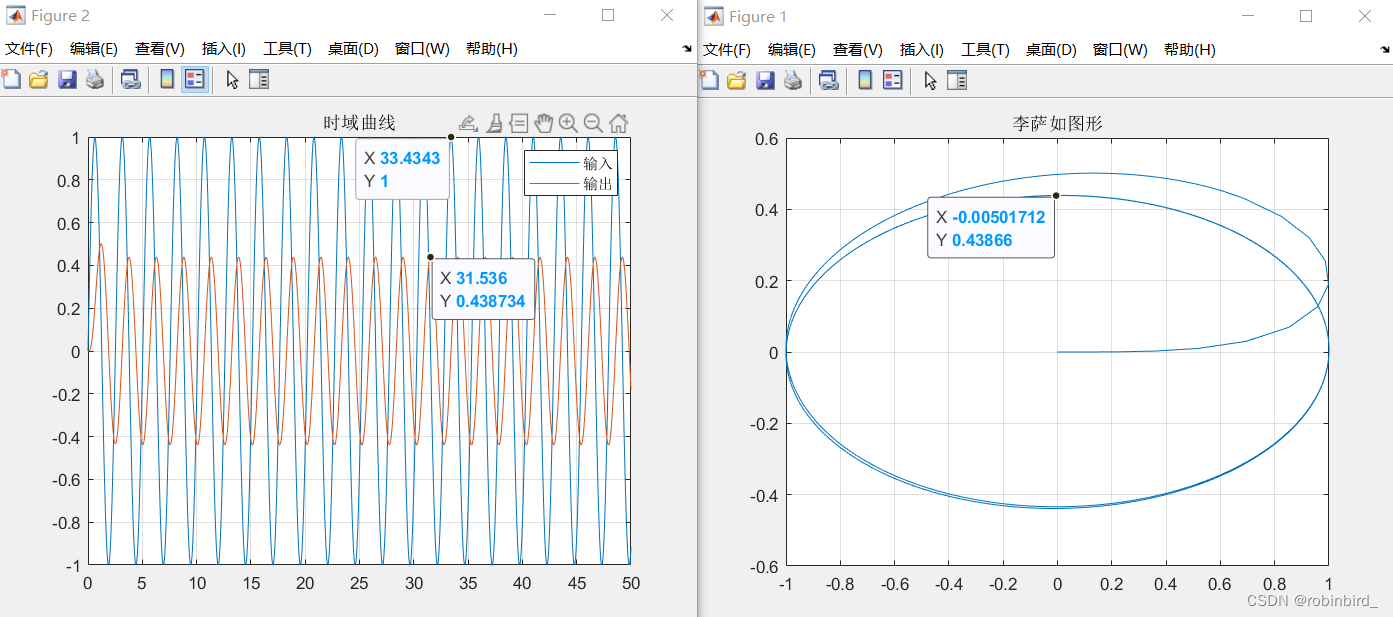
figure; plot(x.signals.values,y.signals.values); title(" Lissajous figure "); grid; figure; plot(x.time,x.signals.values); hold on; plot(y.time,y.signals.values); legend(" Input "," Output "); title(" Time domain curve "); grid;It can be used x( Corresponding to the input of the system ), and y( Corresponding to the output of the system ) Direct use matlab fitting
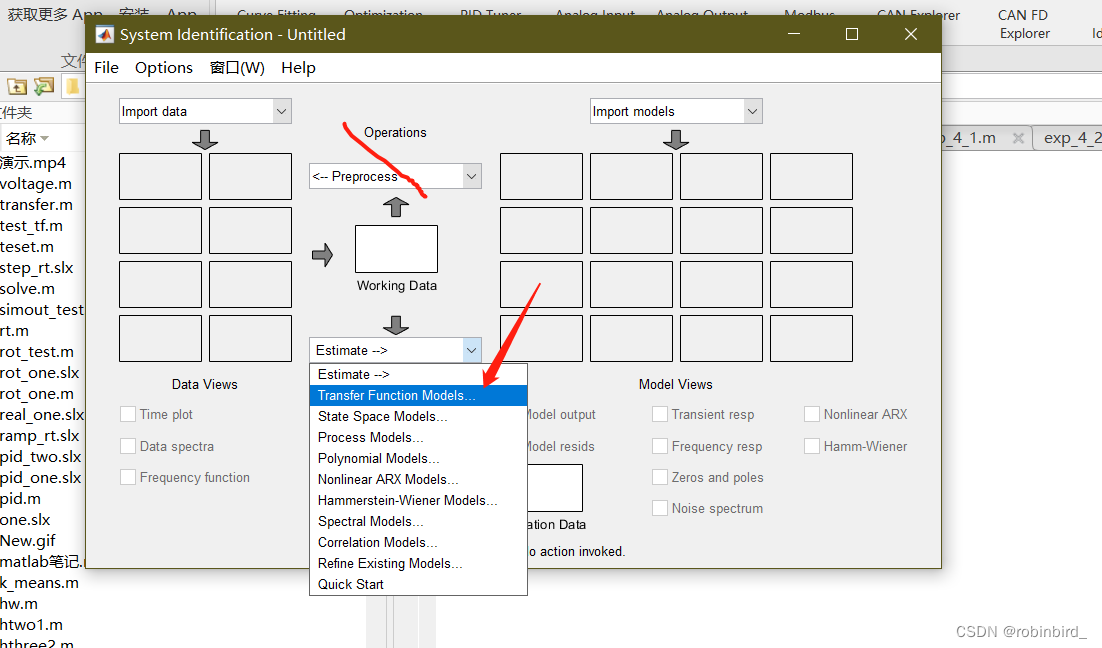
Be careful : First the x,y The data type of is set to 2-D array, It's a two-dimensional array , Then follow the steps in the following article Data import :
http://t.csdn.cn/NrfDU
Next, analyze the link :operations Personally, I don't think it's necessary , The analysis method is the transmittal mode , You need to give the number of zeros and poles ,matlab Direct fitting according to the number of zeros and poles
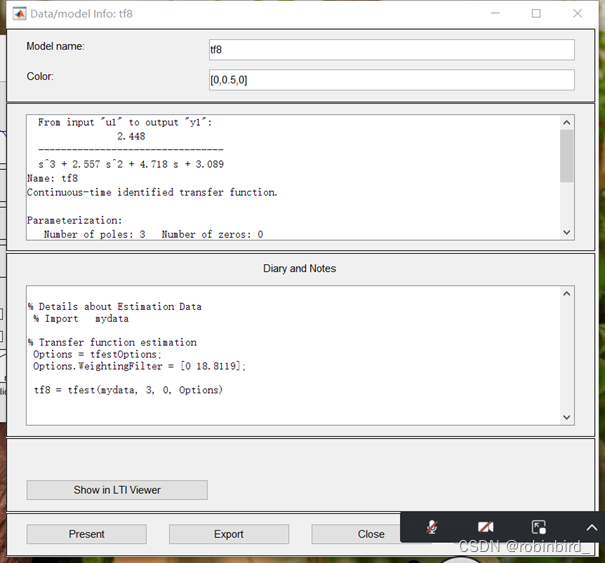
Take the screenshot of your eighth experiment as an example , No zero point was selected at that time ,3 A pole
※ The principle of automatic control makes up the leak ~~( A vegetable dog didn't understand until he finished the exam )~~
Mainly with The higher-order system uses the dominant pole reduction method and Frequency test of , Combined with the specific experimental content of automatic control, briefly explain
1、 Order reduction of dominant poles of higher-order systems
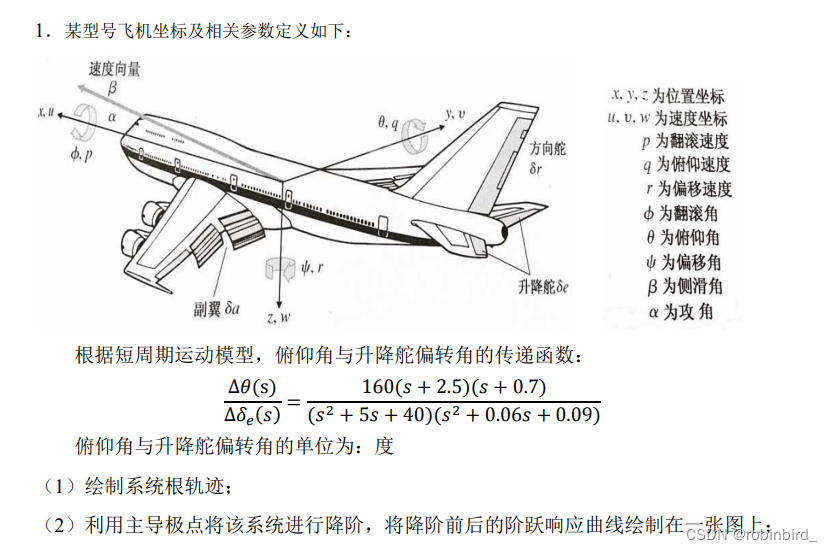
subject ( The first question is ignore ):
Personal understanding : The given transfer function is the open-loop transfer function of this system , And the corresponding root locus gain is 160, If you want to draw, you will get no 160 The transmittal of is passed as a parameter to rlocus Just draw ;
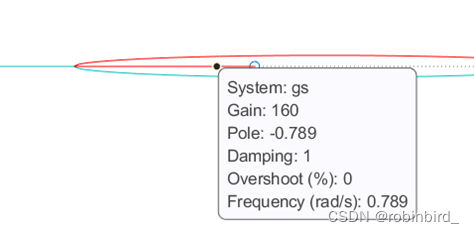
And for order reduction , You need to get in K*=160 All the roots of , Actually use matlab Find the root locus diagram drawn in the diagram 4 It's better to go directly to Casio 991 Solve the equation fragrant , Get more accurate results directly , See tutorial
fx-991CN X equation ( Group ) Use of solving function - Dianzhuo Yuanya Jiliang's article - You know https://zhuanlan.zhihu.com/p/28795401
Theoretical knowledge supplement : First film a wave of explanation from the giant of Harbin Industry :https://www.bilibili.com/video/BV1cK4y1U7jR?share_source=copy_web
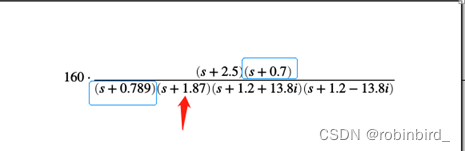
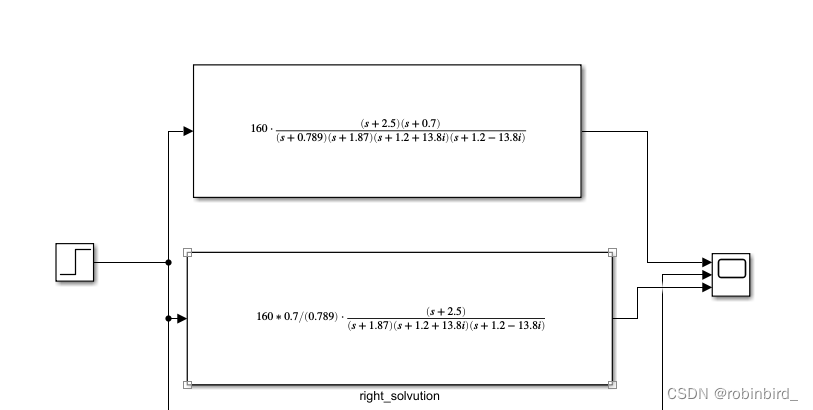
For the reduction of higher-order systems , It is necessary to ensure the stability of the system before and after order reduction Closed loop gain unchanged , So the best way is to get the closed-loop transmittal of the system , Written as closed-loop zero pole form , Then analyze the position of closed-loop zero pole , There are a pair of very close zeros and poles ( Dipole , In the blue box ), Can be removed , remainder The real part of the pole does not 2-3 Times more , Therefore, none of them can be omitted
result : according to K The unchanging principle , Whoever gets rid of it will leave the corresponding constant term , Finally, the step response curve is obtained
2、 Frequency characteristic test
subject :
Add :
(1) The solution of phase and amplitude is as follows , So just need to be in Lissajou image (x For input ,y For export ) Found in Image and x=0 The intersection of the axes , Find in the step response curve Peak value of input / output image Put it in a table , Just draw a picture
R ( t ) = A 0 ∗ s i n ( w t ) C ( t ) = A 1 ∗ s i n ( w t + φ ) A ( w ) = A 1 / A 0 φ ( w ) = a c r s i n ( C ( 0 ) / A 1 ) R(t) = A_{0}*sin(wt)\\ C(t) = A_{1}*sin(wt+φ)\\ A(w) = A1/A0\\ φ(w) = acrsin(C(0)/A1) R(t)=A0∗sin(wt)C(t)=A1∗sin(wt+φ)A(w)=A1/A0φ(w)=acrsin(C(0)/A1)
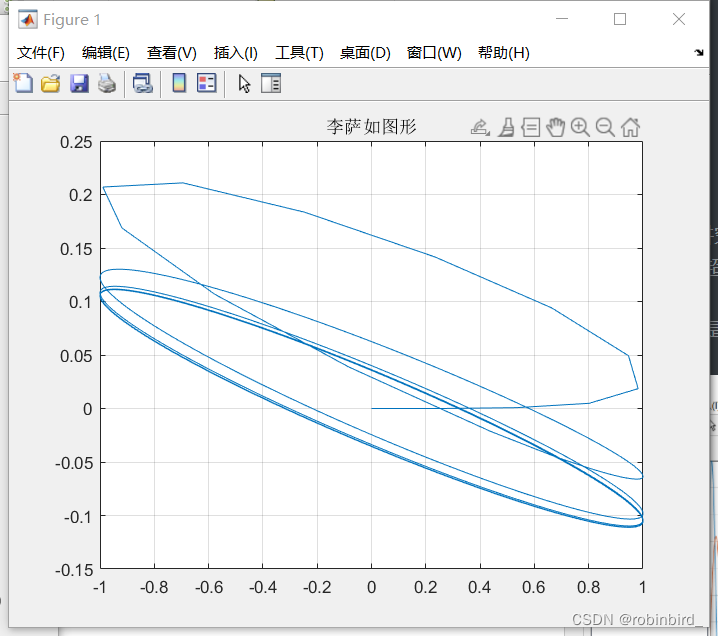
(2) There are also aspects , Lissajou's image is elliptical , The inclination angle of its long axis ( And right x Included angle of shaft ) It's probably the phase difference , So we need to Pay attention to phase override 90°/180°/270° etc. , Modify the corresponding phase solution formula in timeLike this picture , It's a positive ellipse , The phase is close 90°
This is more than 90° 了
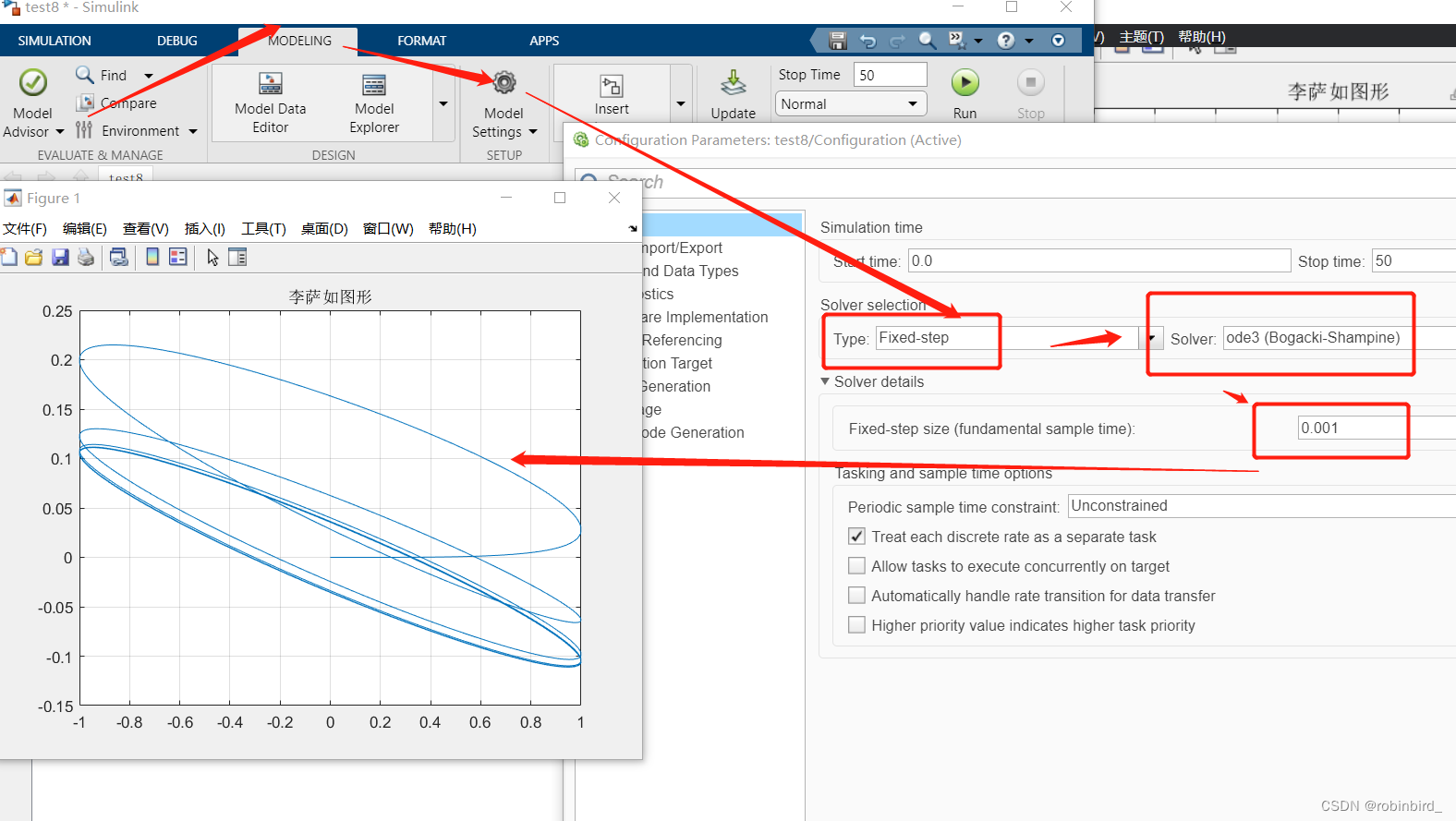
(3) But you can find that the curve above is not smooth enough , So I copied the similar model settings sent by the teacher before , The curve is instantly beautiful : stay simulink Look for this setting in the interface
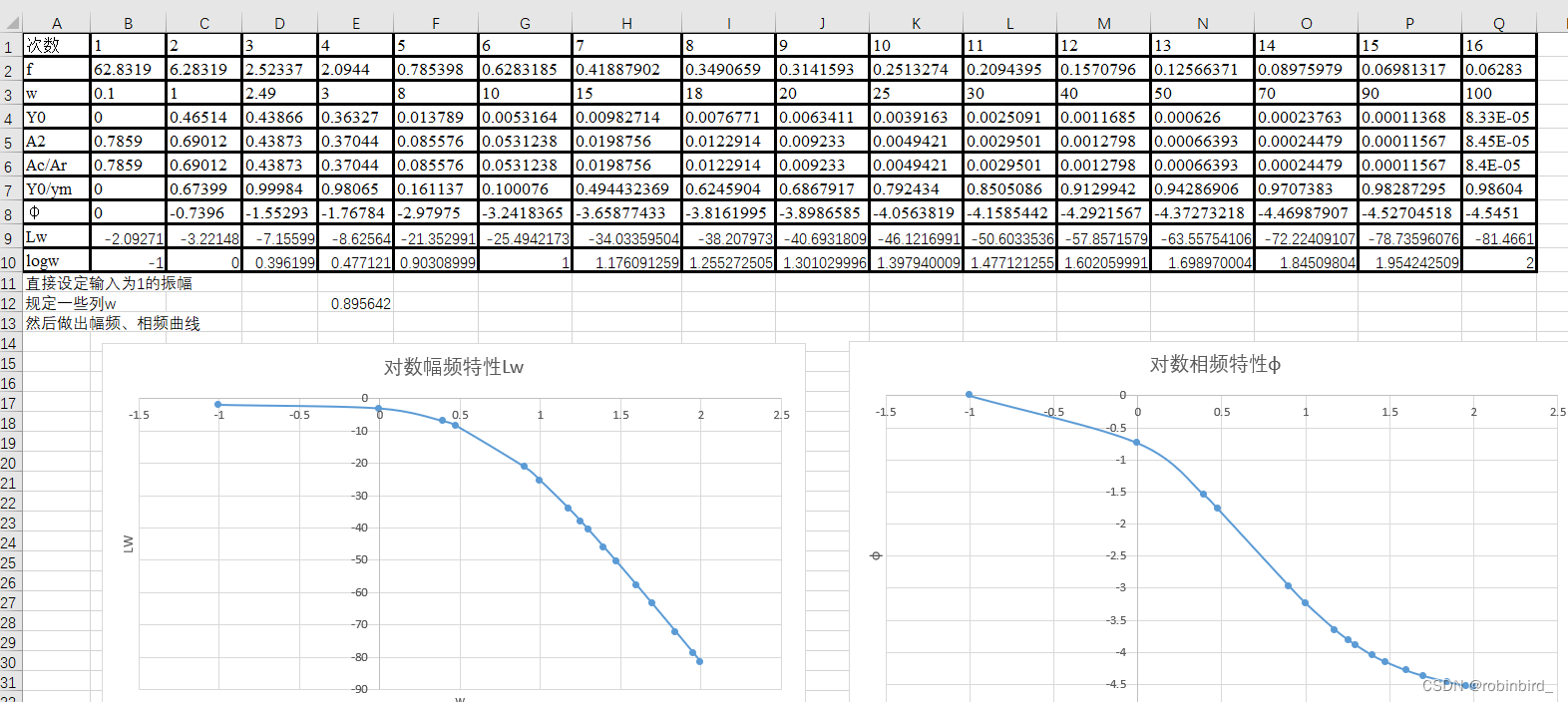
(4) Next is excel processing section , Get organized w/A1/A0/C0 And use excel Function of , Using the type of scatter plot with asymptote , You can get the image of frequency characteristic test , And according to the maximum phase 、 The turning point 、 Initial phase 、 Initial amplitude, etc
(5) Although obviously 3 Order system , But the analysis method of second-order system is also ok 、、、 But this is not recommended ,
system identification Doesn't it smell good; Other ways , For example, some information can be obtained from the curve of step response to fit the functionIt's also a doubt that will be solved after the exam ( Pure is because he sprinkled money ):bode The picture is only for Transfer function The expression of , It has nothing to do with open-loop and closed-loop , It only uses this function The sinusoidal response result of A、φ, So all kinds of typical transmittal links in the book ( inertia 、 Oscillate 、 First and second order differential 、 Integral, etc. ) These results are applicable to the observation of frequency characteristics
automatic control 1 End of the flower **ヽ(°▽°)ノ*, Already a self-control person
边栏推荐
- 3:第一章:认识JVM规范2:JVM规范,简介;
- Shell: operator
- asp. Net pop-up layer instance
- CJ mccullem autograph: to dear Portland
- Detailed explanation of pointer and array written test of C language
- Thoroughly understand JVM class loading subsystem
- 11gR2 Database Services for "Policy" and "Administrator" Managed Databases (文件 I
- C# Linq Demo
- CorelDRAW plug-in -- GMS plug-in development -- new project -- macro recording -- VBA editing -- debugging skills -- CDR plug-in (2)
- Openresty ngx Lua regular expression
猜你喜欢
![[original] what is the core of programmer team management?](/img/11/d4b9929e8aadcaee019f656cb3b9fb.png)
[original] what is the core of programmer team management?
Non rigid / flexible point cloud ICP registration
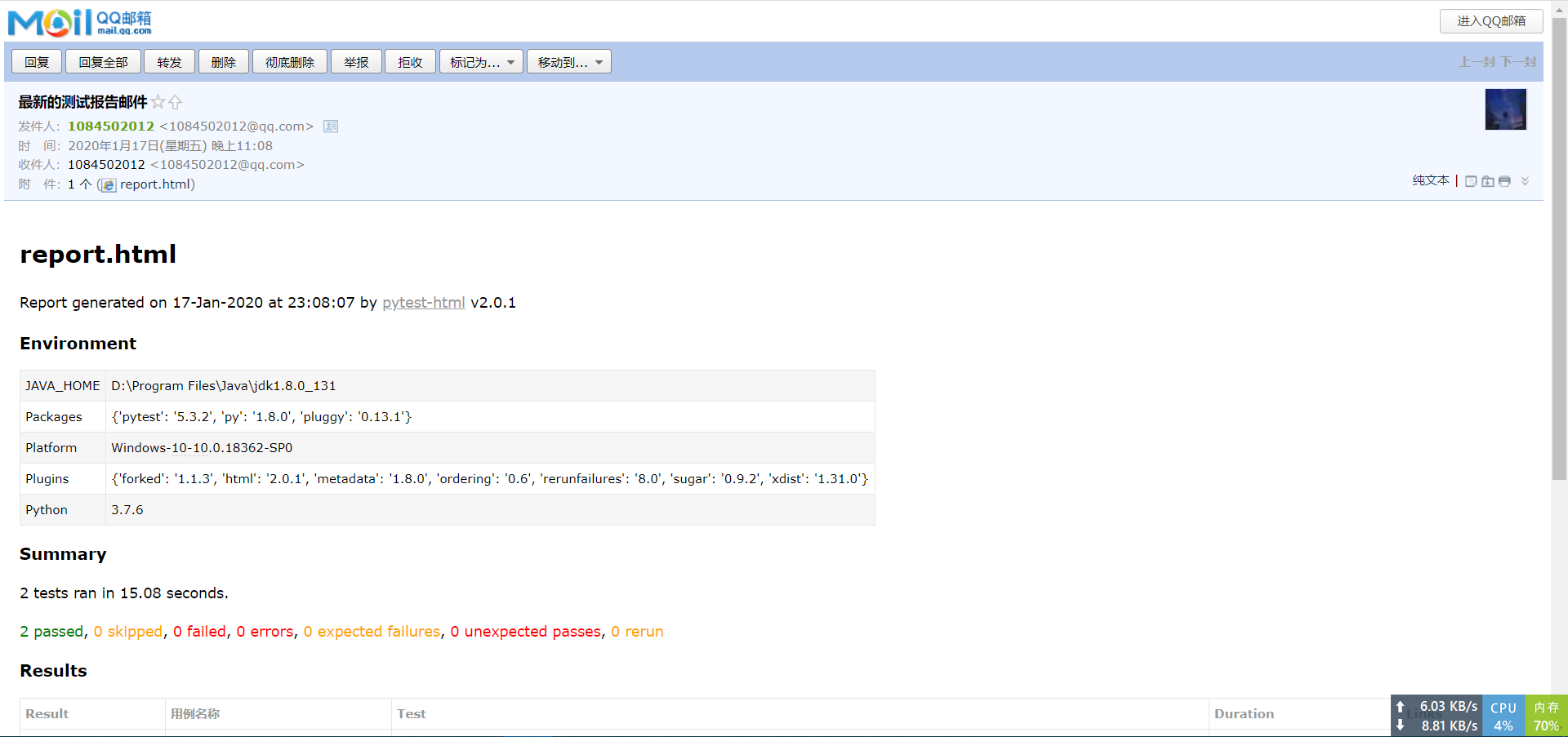
Selenium+Pytest自动化测试框架实战
Initial experience | purchase and activate typora software
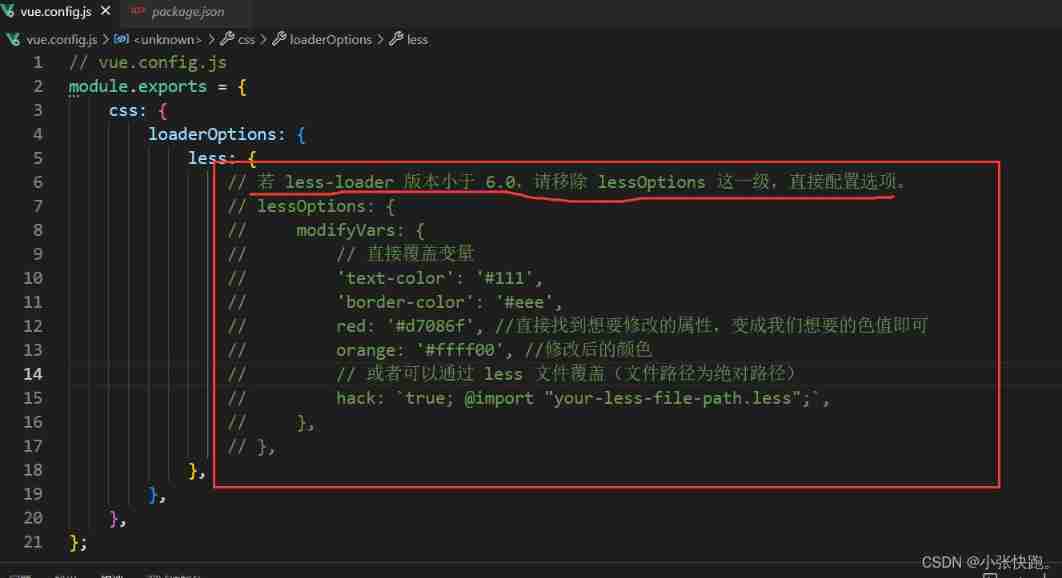
TypeError: this. getOptions is not a function
2022 G3 boiler water treatment simulation examination and G3 boiler water treatment simulation examination question bank
Element positioning of Web Automation
Fix the memory structure of JVM in one article
The method and principle of viewing the last modification time of the web page
【原创】程序员团队管理的核心是什么?
随机推荐
LabVIEW打开PNG 图像正常而 Photoshop打开得到全黑的图像
2:第一章:认识JVM规范1:JVM简介;
698. 划分为k个相等的子集 ●●
White hat talks about web security after reading 2
Solution to the packaging problem of asyncsocket long connecting rod
How to design API return code (error code)?
grafana工具界面显示报错influxDB Error
Design and implementation of secsha system
Krypton Factor purple book chapter 7 violent solution
Object detection based on impulse neural network
Use of shell:for loop
Three. Js-01 getting started
[screen recording] how to record in the OBS area
使用rewrite规则实现将所有到a域名的访问rewrite到b域名
Three.JS VR看房
Negative sampling
golang代码检查工具
Live tiktok shop 2022 latest gameplay card slot overseas live e-commerce new traffic
(4) UART application design and simulation verification 2 - TX module design (stateless machine)
Multi camera stereo calibration
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-doVagqrR-1657012369280)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220420210012659.png)]](/img/b8/1fb921cc61d3d7fa78a648738b252b.png)
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-KrNrLKHm-1657012369284)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220420210717309.png)]](/img/01/eb90e5c3f6fdc64f721be991df9019.png)
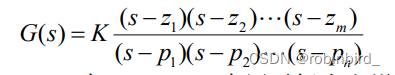
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-joecKule-1657012369287)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220420211133977.png)]](/img/24/ee7194792ce5515dc8333c9ed095f2.png)
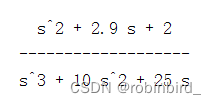
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-22Wx11XX-1657012369297)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220705111245340.png)]](/img/30/5e82f63df8860ba6ab997ac7111120.png)
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-juj7D7RC-1657012369299)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220421100000555.png)]](/img/73/e040fd977aec3081b9d23a8e6dfaae.png)
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-ZF0zAQEi-1657012369301)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220705115014808.png)]](/img/ec/a8a894eb418c8ddbdc45f146784d73.png)
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-N2SWPYb2-1657012369310)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220508110156814.png)]](/img/d3/adb265592247e13514e5e9841572e8.png)
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-ySVKe33P-1657012369310)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220508110214336.png)]](/img/f4/56d245c43d21542cafd052b861faf2.png)
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-WLfDF5oo-1657012369312)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220508110510079.png)]](/img/59/ef16fdd82bfb339fcca55b8ff13632.png)

![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-f2A0Bgbr-1657012369319)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220705161314080.png)]](/img/f1/4d9dc009701819f05ab6ab82dcd51b.png)