当前位置:网站首页>判斷二叉樹是否為完全二叉樹
判斷二叉樹是否為完全二叉樹
2022-07-05 23:01:00 【明朗晨光】
1、題目
給定一棵二叉樹的根節點root,判斷這棵樹是否為完全二叉樹。
2、分析
完全二叉樹就是每一層要麼是滿的,如果不滿也是從左到右依次變滿。
經典做法
按層遍曆,遵循幾個原則:
- 如果某個節點有右孩子,沒有左孩子,則它一定不是完全二叉樹;
- 當第一次遇到左右孩子不雙全的時候,剩下遍曆的節點必須是葉節點,否則不是完全二叉樹。
遞歸套路
目標:X 為頭的二叉樹是否為完全二叉樹;
可能性:分類——最後一層的最後一個節點到哪兒了
① 最後一層節點是滿的:如果左樹是滿的,右樹也是滿的,且左右樹高度一致,則以 X 為頭的這棵二叉樹一定是完全二叉樹。(左樹滿,右樹滿,左高 = 右高)
②最後一層節點不滿:
1) 最後一個節點在左樹,但是左樹沒滿:如果左樹是完全二叉樹,且右樹是滿的,且左樹比右樹高度大1,那麼 X 為頭的這棵二叉樹一定是完全二叉樹。(左完全,右滿,左高 = 右高 + 1)
2)最後一個節點剛好使得左樹滿:左樹是滿的,右樹是滿的,左樹高度比右樹高度大1,那麼 X 為頭的這棵二叉樹一定是完全二叉樹。(左滿,右滿,左高 = 右高+ 1)
3)最後一個節點在右樹上,但是右樹沒滿:左樹是滿的,右樹是完全二叉樹,且左右樹高度一致,那麼 X 為頭的這棵二叉樹一定是完全二叉樹。(左滿,右完全,左高 = 右高)為了支持這 4 種可能性,需要向左右樹收集的信息:(1)是否是滿二叉樹;(2)是否是完全二叉樹;(3)高度。
3、實現
C++ 版
/************************************************************************* > File Name: 041.判斷二叉樹是否為完全二叉樹.cpp > Author: Maureen > Mail: [email protected] > Created Time: 一 7/ 4 19:39:10 2022 ************************************************************************/
#include <iostream>
#include <ctime>
#include <queue>
using namespace std;
class TreeNode {
public:
int value;
TreeNode *left;
TreeNode *right;
TreeNode(int data) : value(data) {
}
};
//方法一:經典做法
bool isCBT1(TreeNode *root) {
if (root == nullptr) return true;
queue<TreeNode*> _que;
bool leaf = true;
TreeNode *l = nullptr;
TreeNode *r = nullptr;
_que.push(root);
while (!_que.empty()) {
root = que.front();
que.pop();
l = root->left;
r = root->right;
//遇到了不雙全的節點且發現當前節點不是葉節點 或 有右孩子無左孩子
if (leaf && (l != nullptr || r != nullptr)) || (l == nullptr && r != nullptr) ) {
return false;
}
if (l != nullptr) {
_que.push(l);
}
if (r != nullptr) {
_que.push(r);
}
if (l == nullptr || r == nullptr) {
//只有一個孩子,就是孩子不雙全的情况
leaf = true;
}
}
return true;
}
//方法二:二叉樹的遞歸套路
class Info {
public:
bool isFull;
bool isCBT;
int height;
Info(bool full, bool cbt, int h) :
isFull(full), isCBT(cbt), height(h) {
}
};
Info *process(TreeNode *x) {
if (x == nullptr) {
retur new Info(true, true, 0);
}
Info *leftInfo = process(x->left);
Info *rightInfo = process(x->right);
int height = max(leftInfo->height, rightInfo->height) + 1;
bool isFull = leftInfo->isFull && rightInfo->isFull && leftInfo->height == rightInfo->height;
bool isCBT = false;
//可能性1:左滿,右滿,左高 = 右高
if (leftInfo->isFull && rightInfo->isFull && leftInfo->height == rightInfo->height) {
isCBT = true;
} else if (leftInfo->isCBT && rightInfo->isFull && leftInfo->height == rightInfo->height + 1) {
//可能性2:左完全,右滿,左高 = 右高 + 1
isCBT = true;
} else if (leftInfo->isFull && rightInfo->isFull && leftInfo->height == rightInfo->height + 1) {
//可能性3:左滿,右滿,左高 = 右高 + 1
isCBT = true;
} else if (leftInfo->isFull && right->isCBT && leftInfo->height == rightInfo->height) {
//可能性4:左滿,右完全,左高 = 右高
isCBT = true;
}
return new Info(isFull, isCBT, height);
}
bool isCBT2(TreeNode *root) {
return process(root)->isCBT;
}
//for test
TreeNode *generate(int level, int maxl, int maxv) {
if (level > maxl || (rand() % 100 / (double)101) < 0.5)
return nullptr;
TreeNode *root = new TreeNode(rand() % maxv);
root->left = generate(level + 1, maxl, maxv);
root->right = generate(level + 1, maxl, maxv);
return root;
}
TreeNode *generateRandomBST(int level, int value) {
return generate(1, level, value);
}
int main() {
srand(time(0));
int maxLevel = 4;
int maxValue = 100;
int testTimes = 1000001;
cout << "Test begin:" << endl;
for (int i = 0; i < testTimes; i++) {
TreeNode *root = generateRandomBST(maxLevel, maxValue);
if (isCBT1(root) != isCBT2(root)) {
cout << "Failed!" << endl;
return 0;
}
if (i && i % 1000 == 0) cout << i << " cases passed!" << endl;
}
cout << "Success!!" << endl;
return 0;
}
Java 版
import java.util.LinkedList;
public class IsCBT {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
//經典做法
public static boolean isCBT1(Node head) {
if (head == null) {
return true;
}
LinkedList<Node> queue = new LinkedList<>();
// 是否遇到過左右兩個孩子不雙全的節點
boolean leaf = false;
Node l = null;
Node r = null;
queue.add(head);
while (!queue.isEmpty()) {
head = queue.poll();
l = head.left;
r = head.right;
if (
// 如果遇到了不雙全的節點之後,又發現當前節點不是葉節點
(leaf && (l != null || r != null))
||
(l == null && r != null) //有右無左的情况
) {
return false;
}
if (l != null) {
queue.add(l);
}
if (r != null) {
queue.add(r);
}
if (l == null || r == null) {
//如果只存在一個孩子或沒有孩子,就是遇到了孩子不雙全的情况
leaf = true;
}
}
return true;
}
//遞歸套路的做法
public static boolean isCBT2(Node head) {
return process(head).isCBT;
}
public static class Info {
public boolean isFull; //是否滿的
public boolean isCBT;// 是否完全二叉樹
public int height; //高度
public Info(boolean full, boolean cbt, int h) {
isFull = full;
isCBT = cbt;
height = h;
}
}
public static Info process(Node x) {
if (x == null) {
//空樹的設置
return new Info(true, true, 0);
}
Info leftInfo = process(x.left);
Info rightInfo = process(x.right);
int height = Math.max(leftInfo.height, rightInfo.height) + 1;
//左右樹都是滿的,且高度一致,就是滿二叉樹
boolean isFull = leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height;
boolean isCBT = false;
//可能性1:左右樹都是滿的,且高度一致
if (leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height) {
isCBT = true;
}
//可能性2:左樹是完全,右樹是滿的,左樹比右樹高1
else if (leftInfo.isCBT && rightInfo.isFull && leftInfo.height == rightInfo.height + 1) {
isCBT = true;
}
//可能性3:左樹是滿的,右樹是滿的,左樹比右樹高1
else if (leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height + 1) {
isCBT = true;
}
//可能性4:左樹是滿的,右數是完全,左右樹高度一致
else if (leftInfo.isFull && rightInfo.isCBT && leftInfo.height == rightInfo.height) {
isCBT = true;
}
return new Info(isFull, isCBT, height);
}
// for test
public static Node generateRandomBST(int maxLevel, int maxValue) {
return generate(1, maxLevel, maxValue);
}
// for test
public static Node generate(int level, int maxLevel, int maxValue) {
if (level > maxLevel || Math.random() < 0.5) {
return null;
}
Node head = new Node((int) (Math.random() * maxValue));
head.left = generate(level + 1, maxLevel, maxValue);
head.right = generate(level + 1, maxLevel, maxValue);
return head;
}
public static void main(String[] args) {
int maxLevel = 5;
int maxValue = 100;
int testTimes = 1000000;
for (int i = 0; i < testTimes; i++) {
Node head = generateRandomBST(maxLevel, maxValue);
if (isCBT1(head) != isCBT2(head)) {
System.out.println("Oops!");
}
}
System.out.println("finish!");
}
}
边栏推荐
- 第十七周作业
- APK加固技术的演变,APK加固技术和不足之处
- [speech processing] speech signal denoising based on Matlab GUI Hanning window fir notch filter [including Matlab source code 1711]
- 一文搞定class的微觀結構和指令
- How to quickly understand complex businesses and systematically think about problems?
- Arduino 测量交流电流
- Marginal probability and conditional probability
- 第一讲:蛇形矩阵
- 东南亚电商指南,卖家如何布局东南亚市场?
- Data type, variable declaration, global variable and i/o mapping of PLC programming basis (CoDeSys)
猜你喜欢
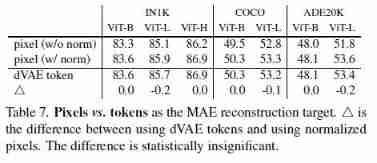
Masked Autoencoders Are Scalable Vision Learners (MAE)

Registration of Electrical Engineering (elementary) examination in 2022 and the latest analysis of Electrical Engineering (elementary)
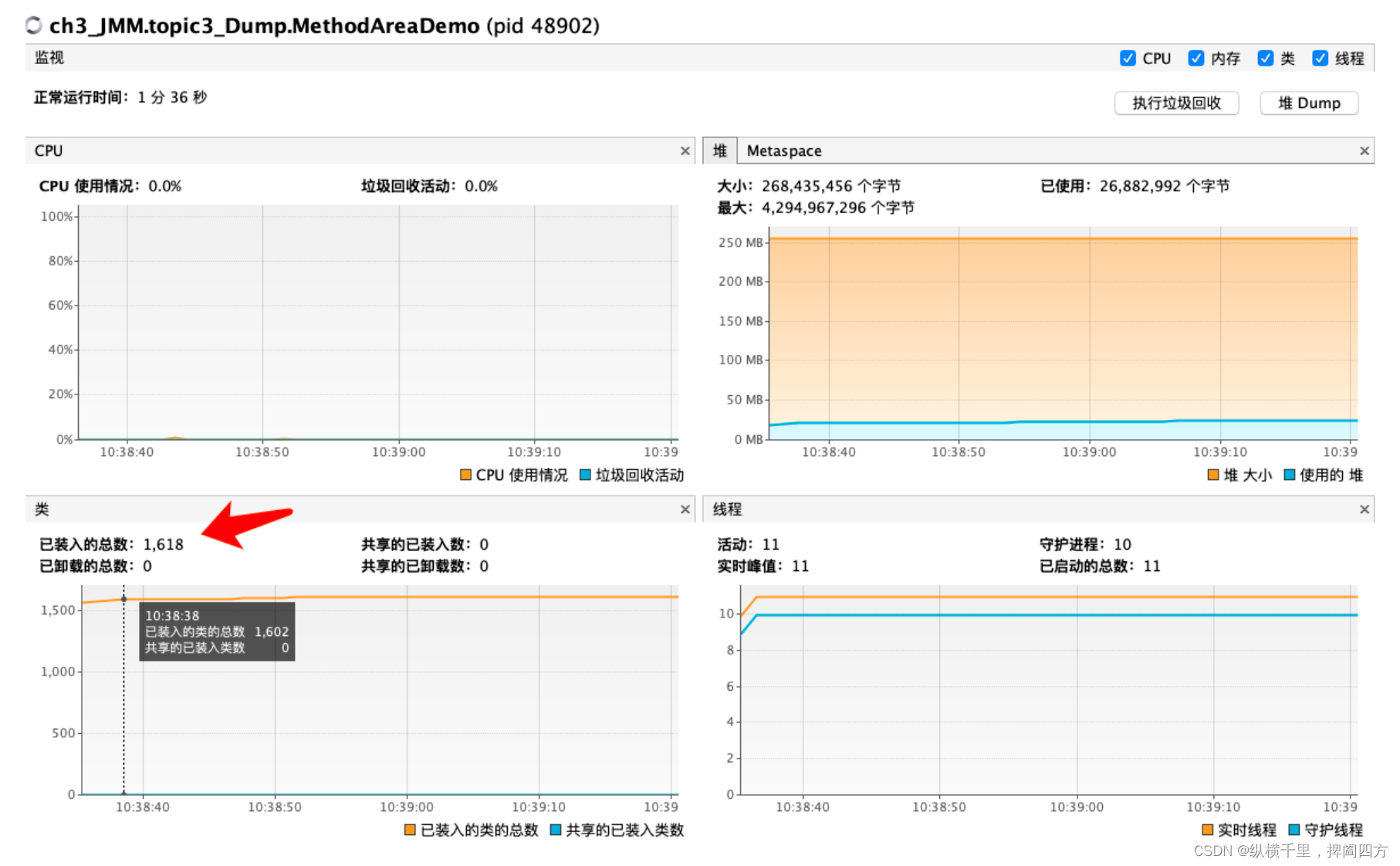
Fix the memory structure of JVM in one article
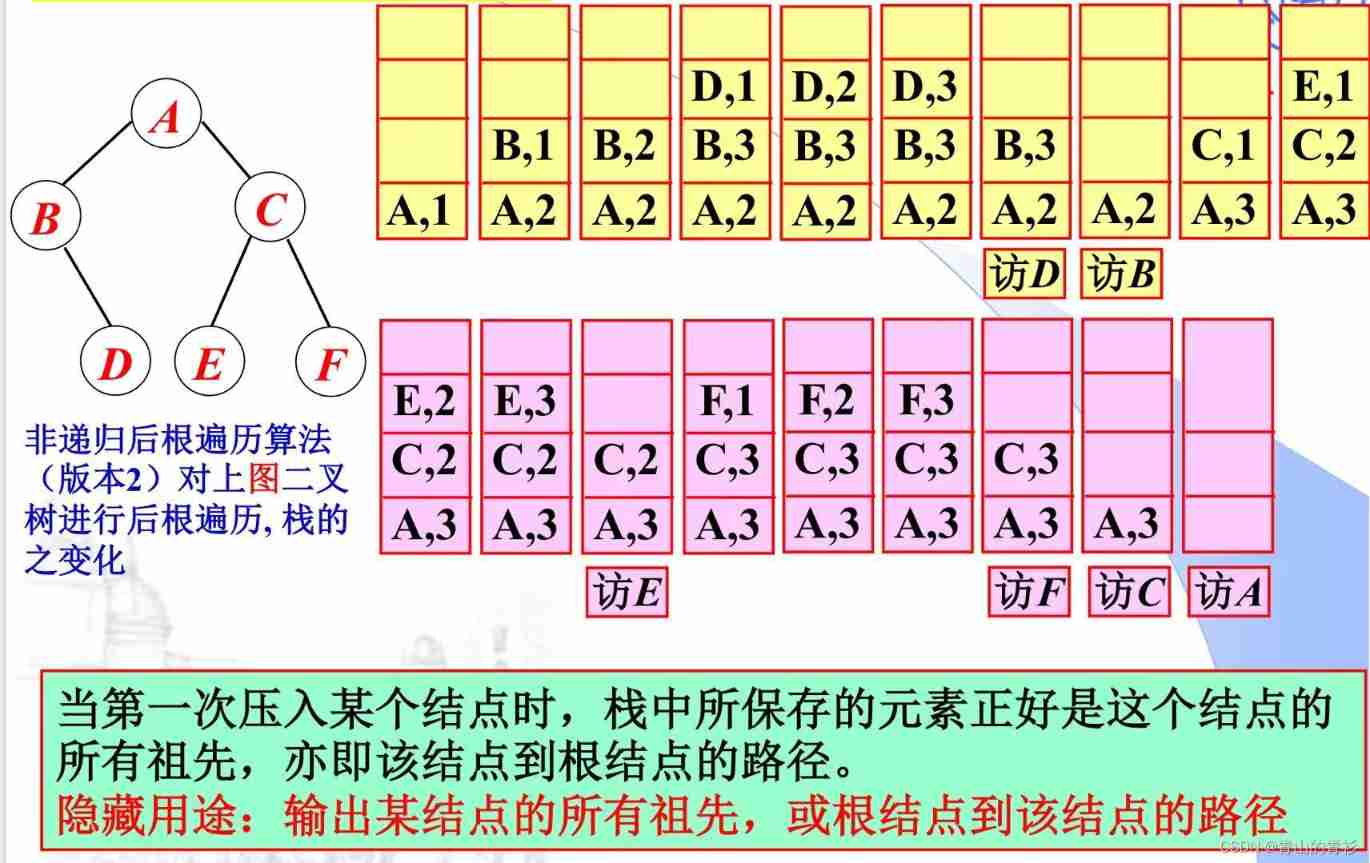
LeetCode145. Post order traversal of binary tree (three methods of recursion and iteration)
利用LNMP实现wordpress站点搭建
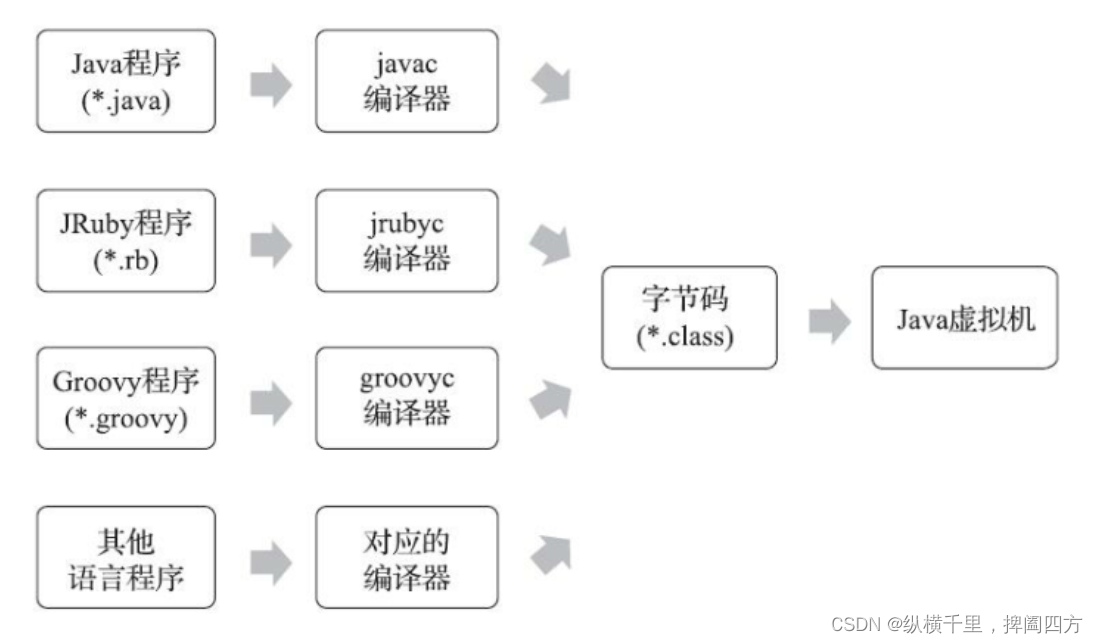
Thoroughly understand JVM class loading subsystem
Ultrasonic sensor flash | LEGO eV3 Teaching

Registration and skills of hoisting machinery command examination in 2022

视频标准二三事

CJ mccullem autograph: to dear Portland
随机推荐
Composition of interface
Methods modified by static
Overview of Fourier analysis
Event trigger requirements of the function called by the event trigger
Hcip day 12 (BGP black hole, anti ring, configuration)
Paddle Serving v0.9.0 重磅发布多机多卡分布式推理框架
Matlab smooth curve connection scatter diagram
Usage Summary of scriptable object in unity
我对新中台模型的一些经验思考总结
媒体查询:引入资源
使用rewrite规则实现将所有到a域名的访问rewrite到b域名
Yiwen gets rid of the garbage collector
Three.js-01 入门
All expansion and collapse of a-tree
Hj16 shopping list
Three. Js-01 getting started
Un article traite de la microstructure et des instructions de la classe
openresty ngx_lua正則錶達式
Expectation, variance and covariance
视频标准二三事