当前位置:网站首页>[combinatorics] exponential generating function (concept of exponential generating function | permutation number exponential generating function = combinatorial number ordinary generating function | e
[combinatorics] exponential generating function (concept of exponential generating function | permutation number exponential generating function = combinatorial number ordinary generating function | e
2022-07-03 18:12:00 【Programmer community】
List of articles
- One 、 Exponential generating function
- Two 、 Permutation number exponential generating function = General generating function of combinatorial number
- 3、 ... and 、 Example of exponential generating function
Reference blog : Look in order
- 【 Combinatorial mathematics 】 Generating function Brief introduction ( Generating function definition | Newton's binomial coefficient | Common generating functions | Related to constants | Related to binomial coefficient | Related to polynomial coefficients )
- 【 Combinatorial mathematics 】 Generating function ( Linear properties | Product properties )
- 【 Combinatorial mathematics 】 Generating function ( Shift property )
- 【 Combinatorial mathematics 】 Generating function ( The nature of summation )
- 【 Combinatorial mathematics 】 Generating function ( Commutative properties | Derivative property | Integral properties )
- 【 Combinatorial mathematics 】 Generating function ( Summary of nature | Important generating functions ) *
- 【 Combinatorial mathematics 】 Generating function ( Generate function examples | Given the general term formula, find the generating function | Given the generating function, find the general term formula )
- 【 Combinatorial mathematics 】 Generating function ( Generate function application scenarios | Solving recursive equations using generating functions )
- 【 Combinatorial mathematics 】 Generating function ( Use the generating function to solve multiple sets r Combinatorial number )
- 【 Combinatorial mathematics 】 Generating function ( Use generating function to solve the number of solutions of indefinite equation )
- 【 Combinatorial mathematics 】 Generating function ( Examples of using generating functions to solve the number of solutions of indefinite equations )
- 【 Combinatorial mathematics 】 Generating function ( Examples of using generating functions to solve the number of solutions of indefinite equations 2 | Extended to integer solutions )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | disorder | Orderly | Allow repetition | No repetition | Unordered and unrepeated splitting | Unordered repeated split )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | Unordered non repeated split example )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | Basic model of positive integer splitting | Disorderly splitting with restrictions )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | Repeated ordered splitting | Do not repeat orderly splitting | Proof of the number of repeated ordered splitting schemes )
One 、 Exponential generating function
Of multiple sets Combinatorial number , Use Generating function Calculate ;
Of multiple sets Number of permutations , Use Exponential generating function Calculate ;
Sequence
{
a
n
}
\{ a_n \}
{ an} , The general formula is
a
n
a_n
an ,
{
a
n
}
\{ a_n \}
{ an} Of The general generating function is
G
(
x
)
=
∑
n
=
0
∞
a
n
x
n
G(x) = \sum\limits_{n=0}^{\infty}a_n x^n
G(x)=n=0∑∞anxn ,
{
a
n
}
\{ a_n \}
{ an} Of The exponential generating function is
G
e
(
x
)
=
∑
n
=
0
∞
a
n
x
n
n
!
G_e(x) = \sum\limits_{n=0}^{\infty}a_n \cfrac{x^n}{n!}
Ge(x)=n=0∑∞ann!xn
\ \ \ \,
* ( Key formula )
{
a
n
}
\{ a_n \}
{ an} Of Exponential generating function It is based on the general generating function Divided by
n
!
n!
n! ;
Two 、 Permutation number exponential generating function = General generating function of combinatorial number
Number of permutations :
P
(
n
,
r
)
=
n
!
(
n
−
r
)
!
P(n,r) = \cfrac{n!}{(n-r)!}
P(n,r)=(n−r)!n! ,
n
n
n Of the elements
r
r
r Elements , Duplicate permutations are not allowed ;
Combinatorial number :
C
(
n
,
r
)
=
n
!
r
!
(
n
−
r
)
!
C(n,r) = \cfrac{n!}{r!(n-r)!}
C(n,r)=r!(n−r)!n! ,
n
n
n Of the elements
r
r
r Elements , Duplicate combinations are not allowed ;
The generating function corresponding to the combination number yes
G
(
x
)
=
∑
n
=
0
∞
(
m
n
)
x
n
G(x) = \sum\limits_{n=0}^{\infty}\dbinom{m}{n} x^n
G(x)=n=0∑∞(nm)xn , After convergence
(
1
+
x
)
n
(1+x)^n
(1+x)n
The generating function corresponding to the permutation number yes
G
(
x
)
=
∑
n
=
0
∞
P
(
m
,
n
)
x
n
G(x) = \sum\limits_{n=0}^{\infty}P(m, n) x^n
G(x)=n=0∑∞P(m,n)xn , according to
n
!
C
(
m
,
n
)
=
P
(
m
,
n
)
n! C(m,n) = P(m, n)
n!C(m,n)=P(m,n) , The generating function of the permutation , Each term is divided by
n
!
n!
n! , You can get the generating function of the corresponding combination number ;
The exponential generating function corresponding to the permutation count yes
G
e
(
x
)
=
∑
n
=
0
∞
P
(
m
,
n
)
x
n
n
!
G_e(x) = \sum\limits_{n=0}^{\infty}P(m, n) \cfrac{x^n}{n!}
Ge(x)=n=0∑∞P(m,n)n!xn , according to according to
C
(
m
,
n
)
=
P
(
m
,
n
)
n
!
C(m,n) =\cfrac{ P(m, n)}{n!}
C(m,n)=n!P(m,n) , It can be concluded as follows :
Exponential generating function of permutation count
=
=
= General generating function of combinatorial counting
3、 ... and 、 Example of exponential generating function
The sequence
b
n
=
1
b_n=1
bn=1 , seek
{
b
n
}
\{ b_n \}
{ bn} The exponential generating function of ;
The sequence is
{
1
,
1
,
1
,
⋯
}
\{1, 1 ,1 , \cdots\}
{ 1,1,1,⋯}
Ordinary generating functions
G
(
x
)
=
1
+
x
+
x
2
+
⋯
=
∑
n
=
0
∞
x
n
G(x) = 1 + x + x^2 + \cdots = \sum\limits_{n=0}^{\infty}x^n
G(x)=1+x+x2+⋯=n=0∑∞xn
Exponential generating function
G
e
(
x
)
=
∑
n
=
0
∞
x
n
n
!
=
e
x
G_e(x) = \sum\limits_{n=0}^{\infty}\cfrac{x^n}{n!}=e^x
Ge(x)=n=0∑∞n!xn=ex
边栏推荐
- This diversion
- Golang string (string) and byte array ([]byte) are converted to each other
- The number of incremental paths in the grid graph [dfs reverse path + memory dfs]
- Computer graduation design PHP makeup sales Beauty shopping mall
- [combinatorics] generating function (use generating function to solve the number of solutions of indefinite equation example 2 | extended to integer solution)
- PHP MySQL order by keyword
- Ssl/bio of OpenSSL_ get_ fd
- MySQL grouping query
- 圖像24比特深度轉8比特深度
- The gbase 8A database does not support the DB2 function value (column_name, 0) cluster syntax
猜你喜欢
![Golang string (string) and byte array ([]byte) are converted to each other](/img/41/20f445ef9de4adf2a2aa97828cb67f.jpg)
Golang string (string) and byte array ([]byte) are converted to each other

Interviewer: why is the value nil not equal to nil?

Have you learned the correct expression posture of programmers on Valentine's day?

Redis on local access server
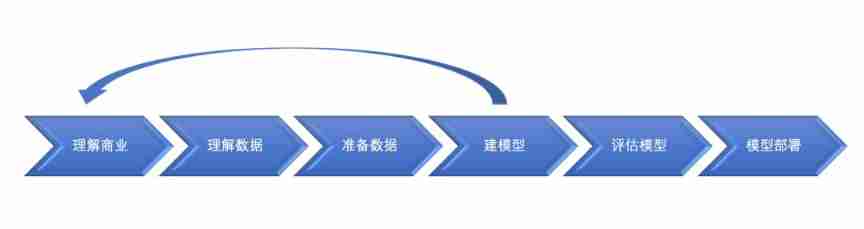
On Data Mining
![Bloom filter [proposed by bloom in 1970; redis cache penetration solution]](/img/f9/27a75454b464d59b9b3465d25fe070.jpg)
Bloom filter [proposed by bloom in 1970; redis cache penetration solution]
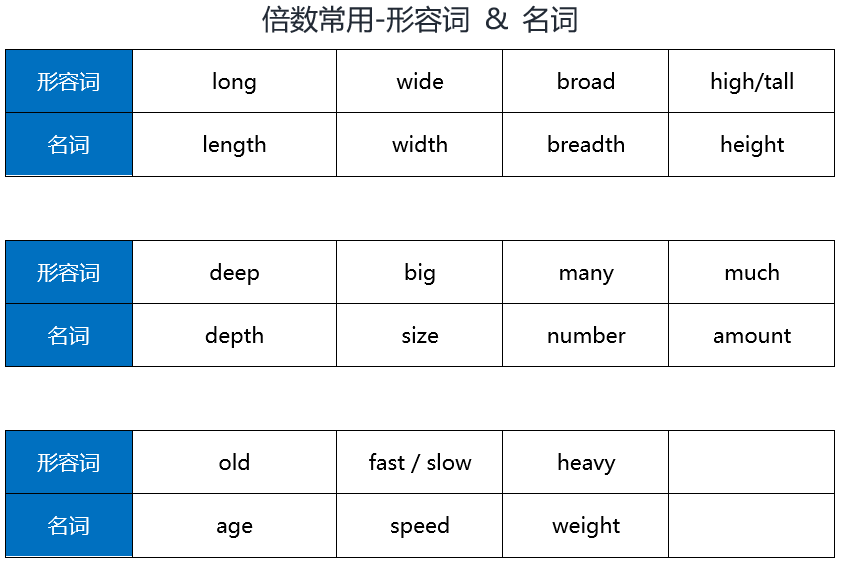
English语法_形容词/副词3级 - 倍数表达
![[untitled]](/img/83/5a57ed90aaafde94db600246256867.jpg)
[untitled]

The third day of writing C language by Yabo people
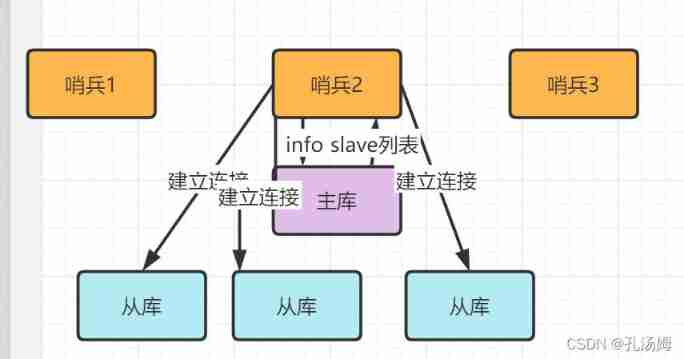
Redis core technology and practice - learning notes (VIII) sentinel cluster: sentinel hung up
随机推荐
[教程]在 CoreOS 上构建你的第一个应用
An academic paper sharing and approval system based on PHP for computer graduation design
How to deploy applications on kubernetes cluster
PHP MySQL reads data
Codeforces Round #803 (Div. 2) C. 3SUM Closure
TCP拥塞控制详解 | 3. 设计空间
Use of unsafe class
Records of long objects and long judgments in the stream of list
ES6类的继承
PHP MySQL order by keyword
SDNUOJ1015
PUT vs. POST for Uploading Files - RESTful API to be Built Using Zend Framework
The third day of writing C language by Yabo people
WebView module manages the application window interface to realize the logical control and management operation of multiple windows (Part 1)
BFS - topology sort
Distributed task distribution framework gearman
Market demand survey and marketing strategy analysis report of global and Chinese pet milk substitutes 2022-2028
Ml (machine learning) softmax function to realize the classification of simple movie categories
[linux]centos 7 reports an error when installing MySQL "no package MySQL server available" no package ZABBIX server MySQL available
分布式的任务分发框架-Gearman