当前位置:网站首页>[reading notes] rewards efficient and privacy preserving federated deep learning
[reading notes] rewards efficient and privacy preserving federated deep learning
2022-07-06 10:36:00 【HERODING23】
Towards Efficient and Privacy-preserving Federated Deep Learning
Preface
An article from the top conference in the communication field ICC The article , The purpose of reading this article is because this article innovatively uses hybrid privacy protection technology , By combining homomorphic encryption and differential privacy , While ensuring data utility , It also reduces the communication cost , Although it is 2019 Articles from , But the idea is still of great help to my future research , I hope to learn more about the core issues of hybrid encryption technology through this article .
One 、 Analysis of the thesis
Abstract
The abstract first mentions the traditional deep learning, which collects data through centralization , Applied in various fields , Distributed deep learning can be trained locally through data , Pass intermediate parameters to improve efficiency and safety , But it will still be attacked by the enemy's reasoning , So this paper combines additive homomorphic encryption and differential privacy , An efficient algorithm based on random gradient descent method is proposed 、 Privatized federal deep learning agreement . Finally, the experiment shows , This scheme has high efficiency and accuracy .
1. INTRODUCTION
Deep learning is widely used , But there is a risk of privacy disclosure , Therefore, federal learning was born , Through distributed training , The way to obtain the intermediate value ensures user privacy . even so , Opponents can still reveal personal information through gradients . Existing solutions include collaborative deep learning models based on selective random gradient descent , Deep learning system with homomorphic encryption , But the former is vulnerable to curious servers , The latter has high communication and computing overhead . So there is the author's idea of combining additive homomorphic encryption with differential privacy , An efficient and privacy preserving federated deep learning scheme based on random gradient descent method . Its advantages are as follows :
- Lightweight , Efficient and safe , Federated learning supporting large-scale applications .
- Using differential privacy based on Laplace mechanism .
- The loss of privacy is negligible , Higher efficiency and accuracy .
2. SYSTEM MODEL AND THREAT MODEL
2.1 System Model
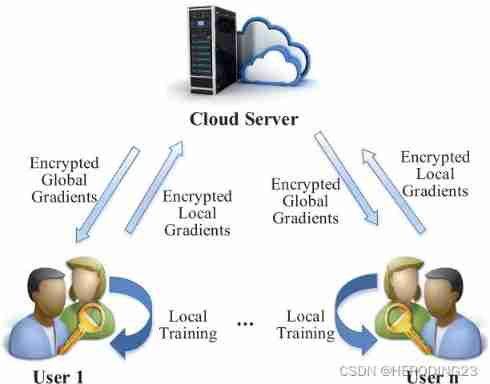
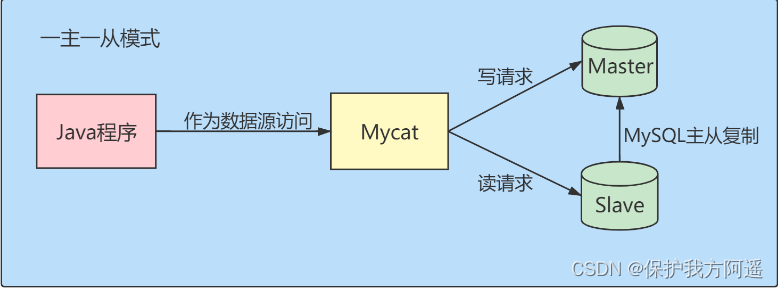
Pictured 1, The system consists of multiple participants and a cloud server , Suppose all participants train a neural network model .
- Participants upload the gradient obtained from local training to ECS , For safety before submission , Interfere with and encrypt data .
- ECS calculates the global gradient on the encrypted gradient , Then broadcast to the participants , Finally, through iterative cooperation , Build a neural network model .
2.2 Threat Model
ECS is considered honest but curious , Information will be extracted from the input of the participants , Another aspect , The protocol should be tolerant of collusion between the server and multiple participants , Therefore, the server is required not to obtain any useful information from the local gradient , Unless the encrypted aggregate result .
3. PRELIMINARIES
This section briefly introduces neural networks and discusses cryptographic primitives that play an important role in this paper .
3.1 Neural Network and Federated Deep Learning
chart 2 It shows the composition of a neural network , Including the input layer , Multiple hidden layers and one output layer , Each layer is composed of multiple neurons , The input data is propagated in each layer through affine transformation and nonlinear activation function processing , For each output result, the random gradient descent method is used to update , The loss function is used as the difference between the predicted result and the actual result .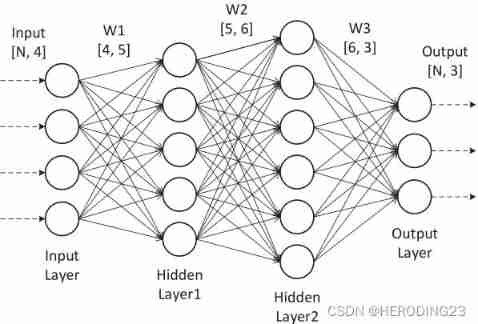
The process of federal learning is mentioned above , No more details here .
3.2 Additively Homomorphic Encryption
Additive homomorphic encryption ensures that the results of multiple ciphertext operations can be successfully decrypted . In this way, participants can outsource encrypted data to ECS for processing without worrying about privacy disclosure . For example, given plaintext m 1 m_{1} m1、 m 2 m_{2} m2, Yes 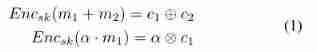 c 1 c_{1} c1 and c 2 c_{2} c2 It's all ciphertext .
c 1 c_{1} c1 and c 2 c_{2} c2 It's all ciphertext .
3.3 ϵ- Differential Privacy and Laplace Mechanism
The first is the concept of differential privacy , In fact, it is two adjacent data sets ( As long as you change the data of any one, it can become another ) If meet 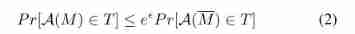 It means that it is satisfied ϵ-DP Of , Generally speaking ,ϵ The smaller it is , The higher the level of privacy protection provided , But the corresponding accuracy will be reduced .
It means that it is satisfied ϵ-DP Of , Generally speaking ,ϵ The smaller it is , The higher the level of privacy protection provided , But the corresponding accuracy will be reduced .
The Laplace mechanism . For query functions f, If the following formula holds , Then mechanism f′ Satisfy ϵ-DP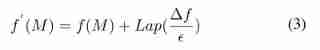 The Laplace mechanism is based on L 1 L_{1} L1 Sensitive , It can be understood as the distance between data vectors , This is also in the formula △ f \bigtriangleup f △f,(3) Type in the Lap It represents the value obtained by satisfying the Laplace distribution .
The Laplace mechanism is based on L 1 L_{1} L1 Sensitive , It can be understood as the distance between data vectors , This is also in the formula △ f \bigtriangleup f △f,(3) Type in the Lap It represents the value obtained by satisfying the Laplace distribution .
4. PROPOSED SCHEME
This part is to introduce the federal learning scheme based on hybrid mechanism and random gradient descent method .
4.1 Overview of Gradients Aggregation Scheme
Homomorphic encryption is widely used to realize the encryption aggregation of ciphertext , But it will significantly increase the computing and communication overhead . however PPDM( Symmetric addition homomorphic encryption ) It's more efficient than , Besides , In order to further improve security and tolerate the withdrawal of participants , Differential privacy .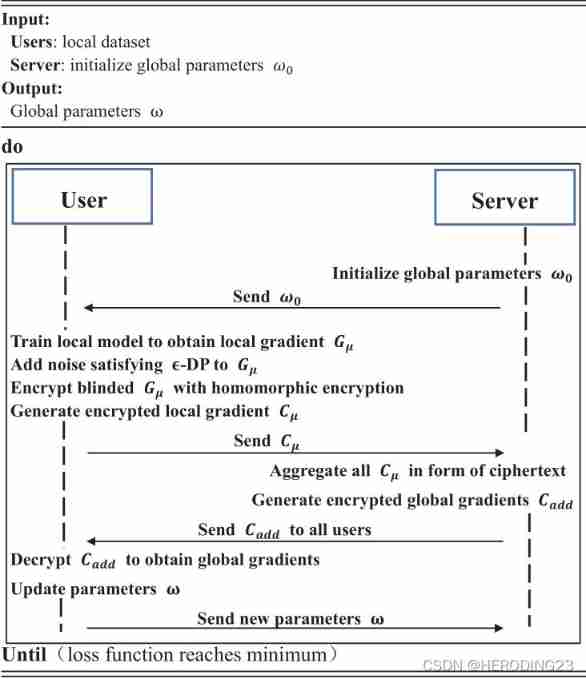 As shown in Figure 3 , For each of these epoch, Every participant µ Use a small number of local data sets to learn the model , And calculate the local gradient Gµ. To protect privacy , Add Laplace noise to the data , And use homomorphic encryption , After receiving the even encryption gradient , Cloud server aggregation :
As shown in Figure 3 , For each of these epoch, Every participant µ Use a small number of local data sets to learn the model , And calculate the local gradient Gµ. To protect privacy , Add Laplace noise to the data , And use homomorphic encryption , After receiving the even encryption gradient , Cloud server aggregation :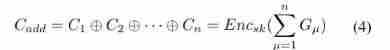
Due to the symmetry of Laplace distribution , The noise is almost eliminated . Final , The party decrypts the encrypted global gradient returned from the server , Then update the parameters ω. In this way , The whole neural network will be built iteratively between ECs and multiple users .
4.2 Efficient and Privacy-preserving Federated Deep Learning
initialization : Original global parameters ω0 And the learning rate η Initialized by ECs . Besides , Given safety parameters λ, Generate the key sk And assign it to all participants , among sk By two large prime numbers p,q(|p |=|q |=λ) form . The public parameter is N=pq.
encryption : To protect the information privacy of participants , All participants choose the same privacy budget ϵ.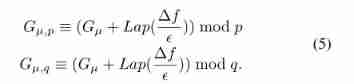
among Gµ Is the local gradient . We assume that each gradient is 0≤ G≤ 1. Using the minimum - Maximum normalization , as well as ∆f It can be set to 1.
then , Use secret key p,q Encrypt the local gradient , As shown below :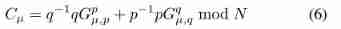
among p − 1 p^{-1} p−1、 q − 1 q^{-1} q−1 Express p and q stay Z ∗ q \mathbb{Z}_{*}^{q} Z∗q The countdown in , Z ∗ q \mathbb{Z}_{*}^{q} Z∗q And encrypted local gradients Cµ Will be sent to ECS .
Secure aggregation :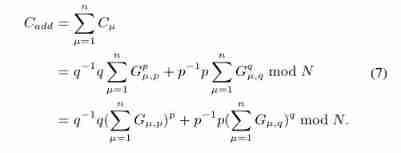
The above equation holds because :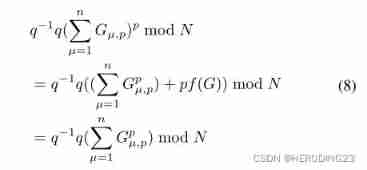
among f(G) Express :
Finally, the server broadcasts the global gradient C a d d C_{add} Cadd.
Decrypt : After receiving the global parameters, the participant decrypts ,
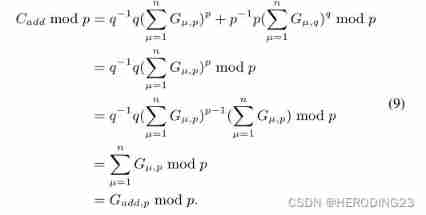
Allied ,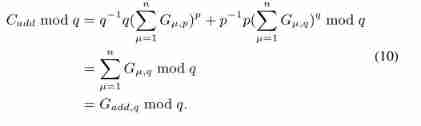 According to Euler's theorem and rolling division , The above formula holds . then , Participants can use the Chinese Remainder Theorem to restore the global gradient G a d d G_{add} Gadd, Calculate this congruence expression :
According to Euler's theorem and rolling division , The above formula holds . then , Participants can use the Chinese Remainder Theorem to restore the global gradient G a d d G_{add} Gadd, Calculate this congruence expression :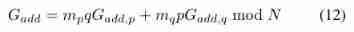
among 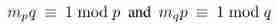 Due to the large number of participants , So we can tolerate the withdrawal of participants . Therefore, it has little effect on eliminating the noise in the disturbance process , namely G a d d G_{add} Gadd Approximately equal to ∑ μ = 1 n G μ \sum _{\mu=1}^{n}G_{\mu} ∑μ=1nGμ. Final , Participants according to ω Update parameters ω←ω− η N \frac{η}{N} Nη Gadd, among N From ECS . Then repeat , Until the termination conditions are met , That is, the minimum value of the loss function defined before .
Due to the large number of participants , So we can tolerate the withdrawal of participants . Therefore, it has little effect on eliminating the noise in the disturbance process , namely G a d d G_{add} Gadd Approximately equal to ∑ μ = 1 n G μ \sum _{\mu=1}^{n}G_{\mu} ∑μ=1nGμ. Final , Participants according to ω Update parameters ω←ω− η N \frac{η}{N} Nη Gadd, among N From ECS . Then repeat , Until the termination conditions are met , That is, the minimum value of the loss function defined before .
5. SECURITY ANALYSIS
This paper mainly focuses on the privacy disclosure of the local gradient of participants .
5.1 Security against the cloud server
Theorem : As long as the above additional homomorphic encryption scheme is CPA Safe , The scheme will not display bit information about a single local gradient .
prove : The encryption scheme in this paper is based on the large integer decomposition problem ,
And it has been proved to be safe . therefore , The model well protects the confidentiality of the individual local gradient of the participants .
5.2 Security against the cloud server and compromised users
Considering the reality , Opponents may endanger some participants , So as to steal the private key of the system and the privacy of honest participants . Differential privacy can provide strict privacy protection .
Theorem : The Laplace mechanism G′µ=Gµ+Lap( △ G ϵ \frac{\bigtriangleup G}{\epsilon } ϵ△G) Maintain Gµ Of ϵ- Differential privacy .
prove : set up χ \chi χ For injection Gµ The noise of , χ \chi χ~Lap( △ G ϵ \frac{\bigtriangleup G}{\epsilon } ϵ△G), set up M M M and M ‾ \overline{M} M Are adjacent data sets , Yes :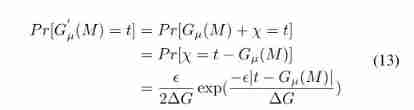 Allied ,
Allied ,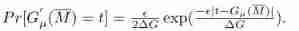 therefore ,
therefore ,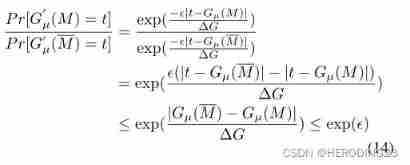
therefore , Gradient disturbances are preserved ϵ-DP, This scheme can tolerate the server colluding with any party , But you can't infer any useful information .
6. PERFORMANCE EVALUATION
The experimental part is related to the latest PPDL Compare , Evaluate the accuracy of the scheme and the communication calculation cost , Pairing encryption is used as the underlying structure .
6.1 Communication overhead
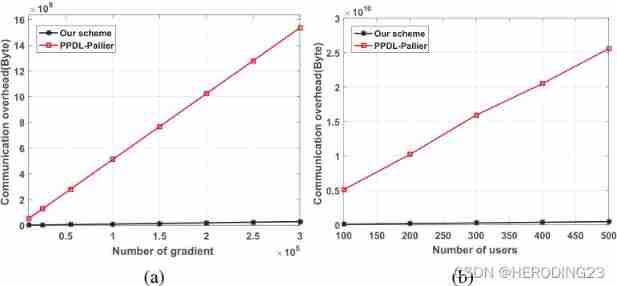
Communication overhead part , First, the experiment is MNIST Use... On datasets TensorFlow Running convolution networks , The gradient comes from 6 m 28×28 Image . chart 4 It shows the communication cost of ECs in one iteration . obviously , As the number of gradients increases , The program cost is PPDL Of 50 Times smaller . One of the main reasons is the use of Paillier After homomorphic encryption, the number of ciphertext increases rapidly . Again , As the number of users increases , The communication cost is much lower than PPDL.
6.2 Computational cost
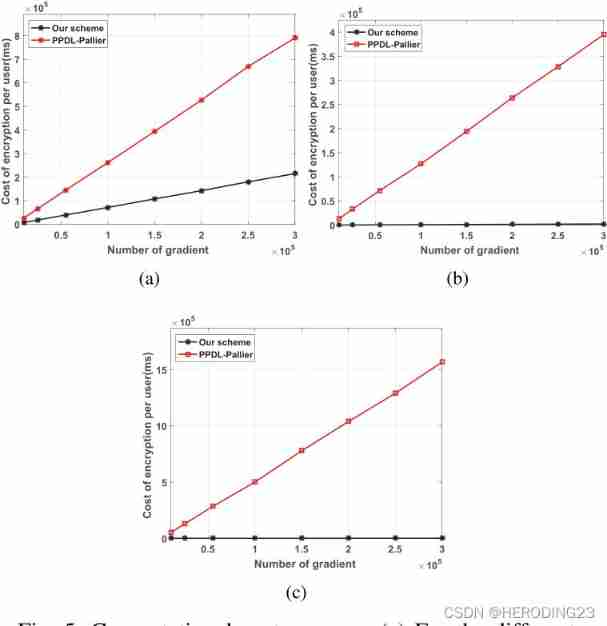
next , This paper discusses the scheme in encryption 、 polymerization 、 The computational cost of decryption . As shown in the figure above , As the number of gradients increases , The cost of encryption is significantly lower than PPDL. Besides , Our aggregation and decryption costs seem to be almost zero , Because they only contain very few multiplication and addition operations . therefore , The scheme proposed in this paper supports the scenario of large-scale participants .
6.3 Accuracy
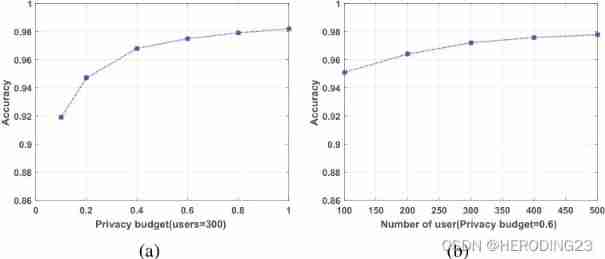
In the evaluation , The influence of the number of users and privacy budget on the classification accuracy of the training model is studied . Under the classification of non private convolution model , Accuracy rate is 98.5%, Under the private convolution model , When the number of users and privacy budget are 300 and 1 when , The solution of this paper will realize 98.1% The accuracy of . Theoretically , Due to the symmetry of Laplace noise , The noise of most participants will be eliminated . therefore , The scheme proposed in this paper can maintain high accuracy .
7. CONCLUSION
In this paper , The author combines additive homomorphic encryption with differential privacy , An efficient and privacy preserving federated deep learning scheme is proposed . The author uses lightweight additive homomorphic encryption to improve efficiency . then , To prevent collusive threats between ECs and multiple users , Further, the differential privacy technology based on symmetric Laplace mechanism is used to disturb the user's original local gradient . Last , A lot of experiments show that , This scheme has high efficiency and accuracy under the non private training model . In the future work , The author will adopt a multi key encryption scheme , To reduce computing overhead .
Two 、 A summary of the paper
This paper innovatively adopts lightweight additive homomorphic encryption technology and differential privacy technology based on Laplace mechanism , An efficient and privacy preserving federated deep learning scheme based on random gradient descent method is implemented . This article starts from the pain point of federal learning ( That is, the gradient information is still vulnerable to the inference attack of the enemy ), Considering communication and computing overhead , Privacy protection method using hybrid mechanism , The security and privacy of the hybrid mechanism are proved . In the experimental part , Through and with PPDL Model comparison , It is proved that the communication overhead of additive homomorphic encryption is much lower than PPDL(50 times smaller), The computational cost is also far less than PPDL, In terms of accuracy , Even if Laplace noise is added , Compared with the accuracy of non privacy, it is almost the same ( Difference between 0.4%), This takes advantage of the symmetry of the Laplace mechanism , The noise of most participants will be eliminated . To make a long story short , The scheme proposed in this paper supports the scenario of large-scale participants , Lightweight and efficient .
3、 ... and 、 Personal perception
This is a thesis that greatly inspired my graduation design work , Including the symmetry of Laplace mechanism, which can eliminate the noise operation in the final polymerization , The lightness of additive homomorphic encryption , And the accuracy of the experiment . My next step is to reproduce the paper , In order to achieve a similar effect .
边栏推荐
- MySQL 29 other database tuning strategies
- If someone asks you about the consistency of database cache, send this article directly to him
- 基于Pytorch肺部感染识别案例(采用ResNet网络结构)
- Record the first JDBC
- Mysql25 index creation and design principles
- MySQL实战优化高手09 生产经验:如何为生产环境中的数据库部署监控系统?
- 百度百科数据爬取及内容分类识别
- MySQL实战优化高手08 生产经验:在数据库的压测过程中,如何360度无死角观察机器性能?
- MySQL的存储引擎
- [paper reading notes] - cryptographic analysis of short RSA secret exponents
猜你喜欢
随机推荐
Mysql28 database design specification
C miscellaneous shallow copy and deep copy
MySQL实战优化高手08 生产经验:在数据库的压测过程中,如何360度无死角观察机器性能?
如何搭建接口自动化测试框架?
Complete web login process through filter
【C语言】深度剖析数据存储的底层原理
Database middleware_ MYCAT summary
Pytorch RNN actual combat case_ MNIST handwriting font recognition
Export virtual machines from esxi 6.7 using OVF tool
数据库中间件_Mycat总结
NLP routes and resources
Preliminary introduction to C miscellaneous lecture document
MySQL33-多版本并发控制
What is the difference between TCP and UDP?
14 medical registration system_ [Alibaba cloud OSS, user authentication and patient]
MySQL Real Time Optimization Master 04 discute de ce qu'est binlog en mettant à jour le processus d'exécution des déclarations dans le moteur de stockage InnoDB.
Nanny hand-in-hand teaches you to write Gobang in C language
Windchill configure remote Oracle database connection
MySQL combat optimization expert 05 production experience: how to plan the database machine configuration in the real production environment?
MySQL combat optimization expert 04 uses the execution process of update statements in the InnoDB storage engine to talk about what binlog is?