当前位置:网站首页>【C语言】深度剖析数据存储的底层原理
【C语言】深度剖析数据存储的底层原理
2022-07-06 09:11:00 【East-sunrise】
目录
一.前言
️️我们在敲代码的时候必不可少的便是各种各样的数据,整型、浮点型...而你又是否了解他们呢?今天我们将深度地剖析数据在内存中的存储原理,并通过一些例题加深掌握程度!研究这些底层原理就像在修炼我们的内功,或许过程有点枯燥,但是终有一天,内功一发,必将光芒四射!接下来就开始我们的修炼吧!!
二.数据类型介绍
1.数据类型及意义
在C语言中有几种基本的内置类型
char //字符数据类型 占用1字节short //短整型 占用2字节int //整形 占用4字节long //长整型 占用4字节(32位环境)或8字节(64位环境)long long //更长的整形 占用8字节float //单精度浮点数 占用4字节double //双精度浮点数 占用8字节
1. 使用这个类型开辟内存空间的大小(大小决定了使用范围)。
2. 如何看待内存空间的视角
2.类型的基本归类
整形家族
charunsigned charsigned charshortunsigned short [int]signed short [int]intunsigned intsigned intlongunsigned long [int]signed long [int]
有人可能会觉得疑问,为什么char是整型呢?不是总叫它字符型吗?
因为字符的本质是ASCII值,是整型,所以char也被划分为整型家族
而我们平常写代码的时候,比如写 int a 其实是默认等价于 signed int a
如果没有特地写unsigned则默认代表为有符号类型
浮点数家族:
floatdouble
构造类型:
> 数组类型> 结构体类型 struct> 枚举类型 enum> 联合类型 union
看到这里或许有人会问,为什么数组类型也算构造类型?
其实像 int arr1[5] 和 int arr2[8]就是不一样的类型
arr1的数据类型是 int[5],而arr2的数据类型是int[8]
另外,int arr[ ] 和 char arr[ ]肯定也是不同类型的吧
所以对于数组来说,定义数组时的元素类型、数组元素个数在变化,他的类型也在变
指针类型:
int *pi;char *pc;float* pf;void* pv;
空类型:
void 表示空类型(无类型)通常应用于函数的返回类型、函数的参数、指针类型
三.整型在内存中的存储
一个变量的创建是要在内存中开辟空间的。空间的大小是根据不同的类型而决定的。
那接下来我们谈谈数据在所开辟内存中到底是如何存储的?
比如 :
int a = 20;
int b = -20;
我们知道为 a 分配四个字节的空间,那又是如何存储的呢?我们接下来来了解
1.原码、反码、补码
计算机中的整数有三种2进制表示方法,即原码、反码和补码。
三种表示方法均有符号位和数值位两部分,符号位都是用0表示“正”,用1表示“负”。
正数的原、反、补码都相同。
负整数的三种表示方法各不相同。
原码:
直接将数值按照正负数的形式翻译成二进制就可以得到原码。
反码:
将原码的符号位不变,其他位依次按位取反就可以得到反码。补码:
反码+1就得到补码。
对于整形来说:数据存放内存中其实存放的是补码。
为什么呢?
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;
同时,加法和减法也可以统一处理(CPU只有加法器)此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路️怎么更好的理解呢?
我们举一个例子:假如现在需要计算机执行1-1的运算?
接着让我们看看在内存中的存储
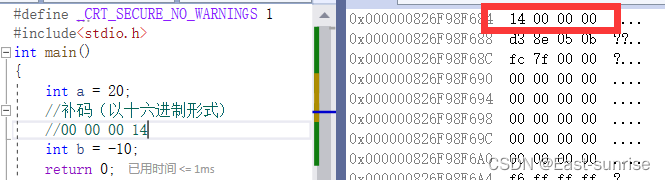
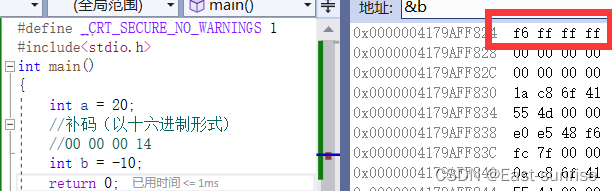
我们可以看到,在内存中是以补码的形式存储的,但是我们发现顺序有点不对劲
这又是为什么呢?
2.大小端的介绍
1.什么是大端小端
大端(存储)模式,是指数据的低位保存在内存的高地址中,而数据的高位,保存在内存的低地址中;
小端(存储)模式,是指数据的低位保存在内存的低地址中,而数据的高位,,保存在内存的高地址中。
我们电脑的内存是从低地址从低到高使用的,每当我们要定义一个变量,便会向内存申请空间用来存储数据。这里假设我们要存储一个数字,11223344(十六进制形式)
因为我们知道,内存空间是以字节为单位的,而我们定义一个四字节十六进制数字来模拟在内存中的存储
就像平时我们日常写数字(十进制)比如写个五百二十:520️
我们很自然的就把高位(5)写在左边,所以大小端存储模式就是一个数字在存储时的高位是在低地址还是高地址的区别
而我们的设备采取哪个存储模式是由设备的硬件设计决定的
2.练习 ️
了解了大小端之后,我们通过一道百度2015年系统工程师笔试题来加深掌握:
请简述大端字节序和小端字节序的概念,设计一个小程序来判断当前机器的字节序。(10分)
其实这道题并不复杂,我们已经知道,大小端存储模式的不同就是存储数据其二进制序列补码的顺序不同。那么我们是否可以输入一个测试数字(越简单明了越好:比如 1)然后取出它在内存中存储时首字节的序列。再通过判断并能得出结论了。️代码展示:
int main() { int a = 1; if (*(char*)&a == 1) printf("小端模式存储"); else printf("大端模式存储"); return 0; }我们选取1作为测试数字的原因是,1的补码为:00000000000000000000000000000001
假如它是小端模式存储,那么我们取出a在内存中存储的首字节序列,就会是1,否则就为大端模式存储。
这里需要注意的是我们运用了一些指针的知识
️指针的类型决定了我们用指针去访问内存的权限(进行操作访问的单位)
整型指针去解引用会访问4个字节,但是我们只想要访问1个字节,那么我们就将其强制转换为char类型再解引用。
可以理解为:我们站在char的角度去访问内存,而char一次访问的是一个字节,解引用就意味着从首地址向后访问一个字节
练习2
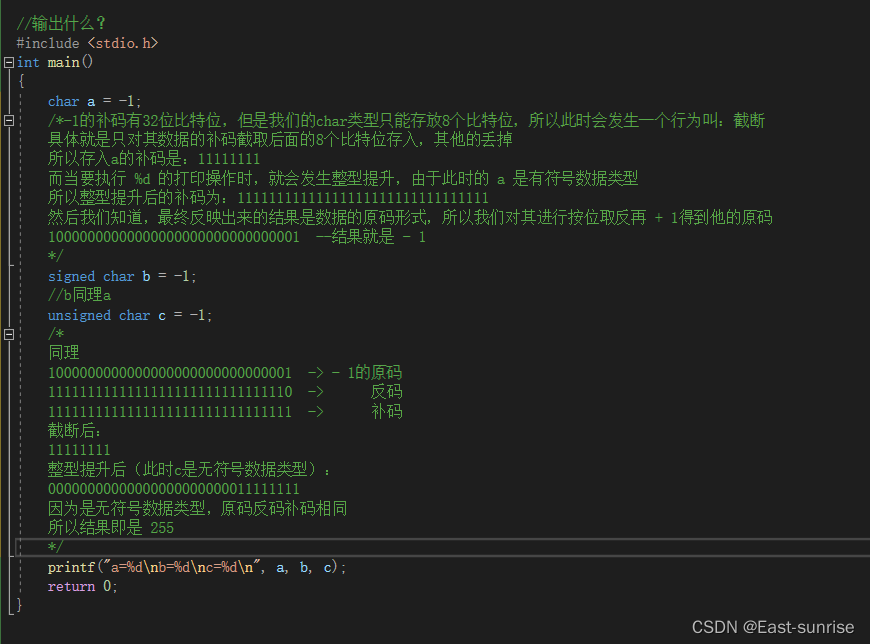
请问:以上代码的运行结果是什么?
🥲没想到吧?接下来由我为你细细解释
首先我们需要知道一个规则概念叫做:整型提升
我们知道 %d 的返回结果是有符号整型 int(该不会不知道吧) 而假设需要执行%d这个动作的数据 a 是一个char类型,或者short类型...这些数据存放字节少于 int 8字节的话就会发生整型提升
发生整型提升的时候是会看a的类型,假如a是无符号数据类型,那么直接对其数据补码高位补0,补够32位比特位。假如a是有符号数据类型,那么会直接将其补码的最高位当作符号位,然后若此符号位为1 则高位补1至一共为32位比特位,同理,若符号位是0,则补0
知道这重要概念后,对于这道题的分析就简单许多了
练习3
下面的代码会输出什么?
int main()
{
unsigned int i;
for (i = 9; i >= 0; i--)
{
printf("%u\n", i);
}
}️输出结果:
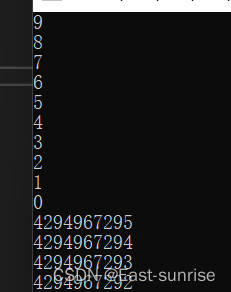
上面代码的输出结果是先输出9~0,然后就开始了我们害怕看到的 死循环!
这又是为什么呢?下面听我跟你娓娓道来
首先我们应该注意到 i 的类型是无符号整型,那么就意味着 i 没有符号位,32位比特位都是有效位,所以我们可以断言:i 一定是大于等于0的!
所以一开始会出现我们熟悉的结果,循环打印到0。
但是这里有一个需要我们注意的是,好比这个程序,for每轮循环之后,是会先执行i --,执行后再进行判断决定是否进入循环。
所以当i变为0之后,减一就得到了 -1 但是我们知道,此时程序的 i 是无符号整型,是恒为正数的,所以问题就出现于此
当i变为 -1 时,我们可以先写出 -1 的二进制补码序列
10000000 00000000 00000000 00000001 --> -1的原码 11111111 11111111 11111111 11111110 --> -1的反码 11111111 11111111 11111111 11111111 --> -1的补码很特殊,-1的补码全是1(我们可以记住),而因为我们这里的 i 是无符号整型,所以i站在一个无符号数的角度看他此时的补码序列,32位1,那就是一个很大很大的正数了 所以会陷入死循环
练习4
下面的代码会输出什么?
int main()
{
char a[1000];
int i;
for(i=0; i<1000; i++)
{
a[i] = -1-i;
}
printf("%d",strlen(a));
return 0;
}️输出结果:
练功练到这里的你,是已经熟能生巧能够推理出正确答案了呢?还是说已经习惯了意想不到的的输出结果而见怪不怪了呢?没事!且听我继续跟你分析
我们注意到最后是要输出strlen函数的返回值,那么我们应该先了解
strlen函数是用于求字符串长度,而他的原理是会计算字符串中‘\0’ 之前有多少个字符,所以一定会找到‘\0’才肯罢休。另外,‘\0’也是一个字符,他的ASCII码值就是0,所以‘\0’也可以等价于0
了解完之后我们再来看这道题
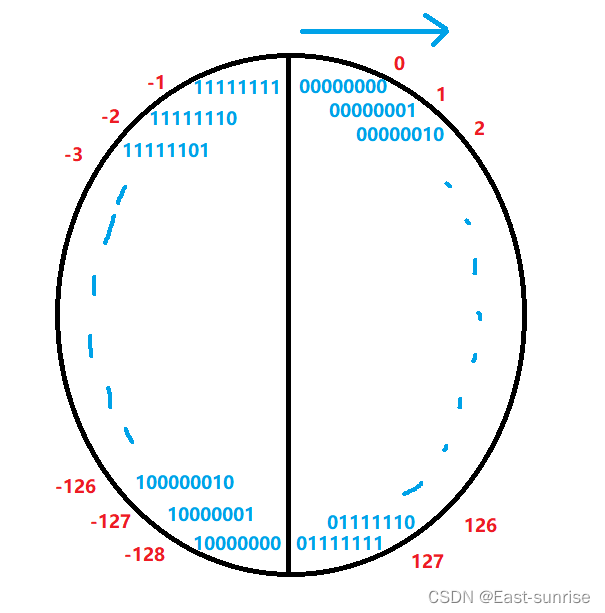
我们可以注意到,数组a的类型是char,并且是有符号类型,而上面我们说过,char类型的取值范围是-128~127.而这个代码就是从a[ 0 ] = -1,a[ 1 ] = -2 这样一直减下去,那等到数组值为-128会发生什么事呢?下面我们借助图来理解
我们知道,char类型是八个比特位,而八个比特位可以表示的数字一共有2^8也就是256个。而如图,假设我们从0开始,每次+1 当我们加到除去符号位其余7个有效位都为1时,也即是最大的正数:127 而当我们再+1时,其二进制序列会变成10000000。注意 这是一个特殊的数值,因为10000000求反码:符号位不变,其余取反:11111111,我们会得到8个1,而再+1求补码就会多出一位,溢出了char的内存空间。因此,c语言规定了char类型中,10000000表示 -128 然后当我们继续+1,便会像时钟一样,一圈一圈的走着,char的数值在-128~127之间按顺序循环着。综上所述,char类型数据的大小范围是 -128~127
而了解完之后我们回归题目,因为数组类型就是char类型,所以题目中数组a的取值便是-1 -2 -3 -4 ... -128 127 126 ...2 1 0 -1 -2....
最后因为一开始我们说了,strlen函数便是计算‘\0’之前出现的字符个数,所以就是255个
练习5
下面的代码输出结果是什么?
#include <stdio.h>
unsigned char i = 0;
int main()
{
for(i = 0;i<=255;i++)
{
printf("hello world\n");
}
return 0; }不出意外的话它会出意外 这个代码的输出结果是 死循环
️如果你已经深刻记得无符号char类型的取值范围是 0~255,又能在第一时间敏锐的注意到 i 就是无符号char类型,那么应该就不难推出结果。
正是因为i是0~255,也即是恒小于等于255,那么下面的for循环岂不是就恒成立了?那么就是死循环!
好了,经过几道有趣且特别的题目,此时身经百战的你是否能够感觉到对数据类型及数据存储规则的掌握又加深了不少呢?而通过这几道题我们应该总结出:在以后的编程中,一定要主意好无符号数据类型和有符号数据类型,不然一不小心就很容易死循环噢!
四.浮点型在内存中的存储
常见的浮点型
3.14159
1E10 (科学计数法,表示:1.0*10的10次方 )
浮点数家族包括: float、double、long double 类型。
浮点数表示的范围:float.h中定义
1.一个例子
在进入浮点型内存存储介绍前,我们先来看一道题,假如你现在就能准确说出答案,那表示你对浮点型内存存储规则已大致掌握。
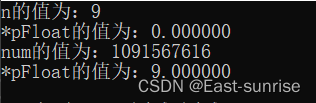
问:此程序的输出结果是什么?
哇哦,是不是有点意想不到?
num 和 *pFloat 在内存中明明是同一个数,为什么浮点数和整数的解读结果会差别这么大?
要理解这个结果,一定要搞懂浮点数在计算机内部的表示方法
2.浮点数存储规则
根据国际标准IEEE(电气和电子工程协会) 754,任意一个二进制浮点数V可以表示成下面的形式:
- (-1)^S * M * 2^E
- (-1)^S表示符号位,当S=0,V为正数;当S=1,V为负数。
- M表示有效数字,大于等于1,小于2。
- 2^E表示指数位。
举例来说:
十进制的5.0,写成二进制是 101.0 ,相当于 1.01×2^2 。
那么,按照上面V的格式,可以得出S=0,M=1.01,E=2。
十进制的-5.0,写成二进制是 -101.0 ,相当于 -1.01×2^2 。那么,S=1,M=1.01,E=2。
IEEE 754规定:
对于32位的浮点数,最高的1位是符号位s,接着的8位是指数E,剩下的23位为有效数字M。

对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M。

IEEE 754对有效数字M和指数E,还有一些特别规定。
前面说过, 1≤M<2 ,也就是说,M可以写成 1.xxxxxx 的形式,其中xxxxxx表示小数部分。
IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的
xxxxxx部分。比如保存1.01的时
候,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的,是节省1位有效数字。以32位
浮点数为例,留给M只有23位,将第一位的1舍去以后,等于可以保存24位有效数字。
至于指数E,情况就比较复杂。
首先,E为一个无符号整数(unsigned int)
这意味着,如果E为8位,它的取值范围为0~255;如果E为11位,它的取值范围为0~2047。但是,我们知道,科学计数法中的E是可以出现负数的,所以IEEE 754规定,存入内存时E的真实值必须再加上一个中间数。
对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。
比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
然后,指数E从内存中取出还可以再分成三种情况:
E不全为0或不全为1
这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将
有效数字M前加上第一位的1。
比如:
0.5(1/2)的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为
1.0*2^(-1),其阶码为-1+127=126,表示为
01111110,而尾数1.0去掉整数部分为0,补齐0到23位00000000000000000000000,则其二进制表示形式为:0 01111110 00000000000000000000000
E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值,
有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字。
E全为1
这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s)
好了,关于浮点数的表示规则,就说到这里。
️解释前面的题目:

下面,让我们回到一开始的问题:为什么 0x00000009 还原成浮点数,就成了 0.000000 ?
首先,将 0x00000009 拆分,得到第一位符号位s=0,后面8位的指数 E=00000000 ,
最后23位的有效数字M=000 0000 0000 0000 0000 1001。
9 -> 0000 0000 0000 0000 0000 0000 0000 1001 由于指数E全为0,所以符合上一节的第二种情况。因此,浮点数V就写成:
V=(-1)^0 × 0.00000000000000000001001×2^(-126)=1.001×2^(-146)
显然,V是一个很小的接近于0的正数,所以用十进制小数表示就是0.000000。
通过这部分解释,其实我们能够知道:我们以浮点数形式存入的话,就要以浮点数的形式取出,其他同理。
当我们以浮点数的形式取出时,就是站在float的视角去看,所以就会认为这个数字就是浮点数,所以就直接将其补码序列以浮点数的存储规则去看待和处理。
再看例题的第二部分。
请问浮点数9.0,如何用二进制表示?还原成十进制又是多少?
首先,浮点数9.0等于二进制的1001.0,即1.001×2^3。
9.0 -> 1001.0 ->(-1)^01.0012^3 -> s=0, M=1.001,E=3+127=130
那么,第一位的符号位s=0,有效数字M等于001后面再加20个0,凑满23位,指数E等于3+127=130, 即10000010。
所以,写成二进制形式,应该是s+E+M,即
0 10000010 001 0000 0000 0000 0000 0000
五.总结
在我们敲代码的时候,我们时时刻刻都在和数据打交道,所以我们更应该去了解他,和他好好相处,才不会容易出现类似死循环等的bug惩罚~~
今天的分享就到此结束啦!如果有什么错误的地方欢迎大佬指正~
如果看到这里不妨给个三连噢~
边栏推荐
- Not registered via @enableconfigurationproperties, marked (@configurationproperties use)
- C miscellaneous shallow copy and deep copy
- MySQL实战优化高手05 生产经验:真实生产环境下的数据库机器配置如何规划?
- MySQL实战优化高手12 Buffer Pool这个内存数据结构到底长个什么样子?
- MySQL combat optimization expert 03 uses a data update process to preliminarily understand the architecture design of InnoDB storage engine
- 13 medical registration system_ [wechat login]
- Some thoughts on the study of 51 single chip microcomputer
- The appearance is popular. Two JSON visualization tools are recommended for use with swagger. It's really fragrant
- What should the redis cluster solution do? What are the plans?
- Canoe cannot automatically identify serial port number? Then encapsulate a DLL so that it must work
猜你喜欢

实现微信公众号H5消息推送的超级详细步骤
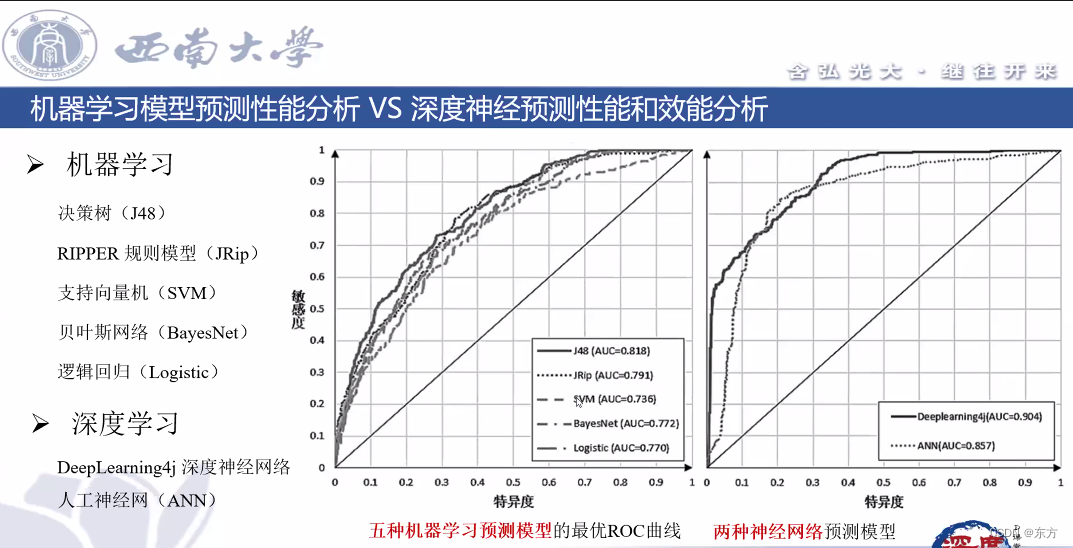
西南大学:胡航-关于学习行为和学习效果分析
![16 medical registration system_ [order by appointment]](/img/7f/d94ac2b3398bf123bc97d44499bb42.png)
16 medical registration system_ [order by appointment]
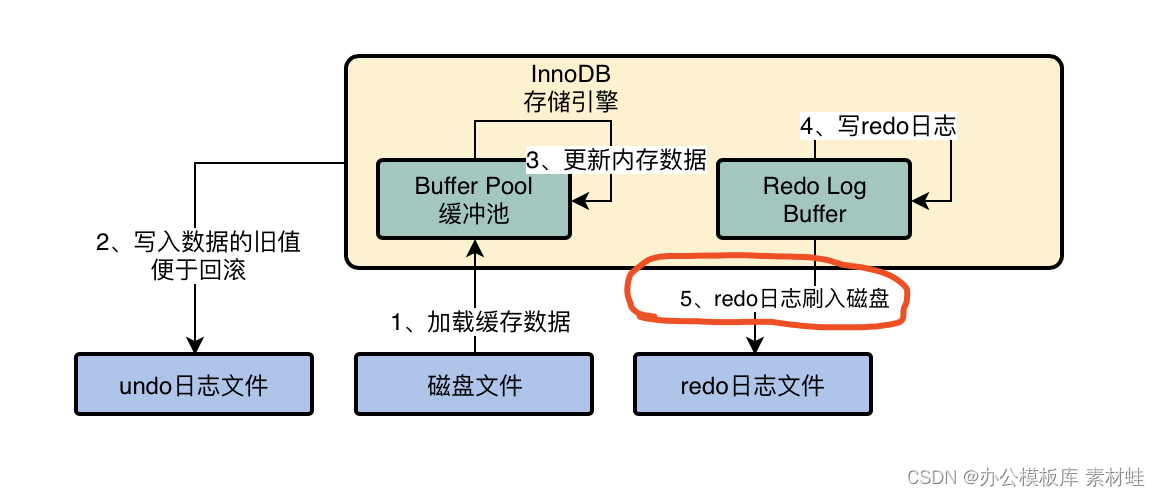
MySQL combat optimization expert 03 uses a data update process to preliminarily understand the architecture design of InnoDB storage engine

MySQL实战优化高手03 用一次数据更新流程,初步了解InnoDB存储引擎的架构设计
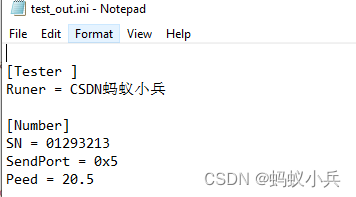
CAPL script pair High level operation of INI configuration file

The 32 year old programmer left and was admitted by pinduoduo and foreign enterprises. After drying out his annual salary, he sighed: it's hard to choose
宝塔的安装和flask项目部署
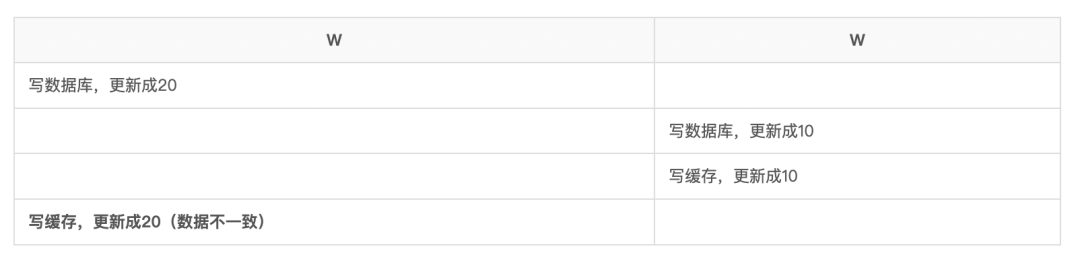
If someone asks you about the consistency of database cache, send this article directly to him

Some thoughts on the study of 51 single chip microcomputer
随机推荐
Solution to the problem of cross domain inaccessibility of Chrome browser
Constants and pointers
Implement sending post request with form data parameter
Competition vscode Configuration Guide
[flask] crud addition and query operation of data
实现以form-data参数发送post请求
颜值爆表,推荐两款JSON可视化工具,配合Swagger使用真香
The 32 year old programmer left and was admitted by pinduoduo and foreign enterprises. After drying out his annual salary, he sighed: it's hard to choose
UEditor国际化配置,支持中英文切换
实现微信公众号H5消息推送的超级详细步骤
MySQL实战优化高手03 用一次数据更新流程,初步了解InnoDB存储引擎的架构设计
How to build an interface automation testing framework?
华南技术栈CNN+Bilstm+Attention
C miscellaneous shallow copy and deep copy
14 医疗挂号系统_【阿里云OSS、用户认证与就诊人】
A necessary soft skill for Software Test Engineers: structured thinking
Simple solution to phpjm encryption problem free phpjm decryption tool
oracle sys_ Context() function
[CV] target detection: derivation of common terms and map evaluation indicators
How to make shell script executable