Master binary tree in one article

A tree structure

Tree is a kind of nonlinear data structure , It is from n Finite nodes make up a set with hierarchical relationships . Because it looks like an upside down tree , So it is called tree structure .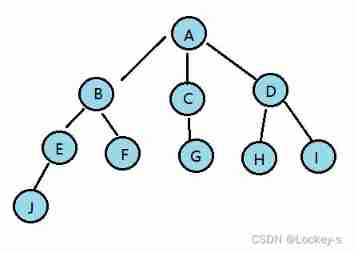

As a subtree, the tree structure cannot have intersection , Otherwise, it is not a tree structure .

Degree of node

The number of subtrees in a node is called the degree of that node , Here's the picture A The degree of is 6 ：

The degree of a tree

In a tree , The maximum degree of all nodes is called the degree of the tree , As shown in the figure below ,A The degree of , So the degree of a tree is 6 ：

Leaf node or terminal node

Degree is 0 The nodes of are called leaf nodes ; Here's the picture ：B、C、H、I… Equal nodes are leaf nodes ：

Parent node or parent node

If a node has children , Then this node is called the parent node of its child node ; Here's the picture ：A yes B The parent node

Child node or child node

The root node of the subtree contained in a node is called the child node of the node ; Here's the picture ：B yes A The child node of

The root node

In a tree , Nodes without parents ： As shown in the figure below ：A

The hierarchy of nodes

Starting from the root , The root for the first 1 layer , The child node of the root is 2 layer , And so on , Like the picture below P Q It's on the fourth floor .

The height or depth of a tree

The maximum level of nodes in a tree ; Here's the picture ： The height of the tree is 4

Brother node

Nodes with the same parent node are called brothers to each other ; Here's the picture ：B、C It's a brotherhood

Tree representation

There are many ways to express the tree structure ： Parenting 、 Child representation 、 The expression of children's parents 、 Child brother notation wait , What we often use is Child brother notation .

class Node {
    
	int value; //  Data stored in the tree 
	Node firstChild; //  The first child quoted 
	Node nextBrother; //  The next brother quotes 
}

Here's the picture ：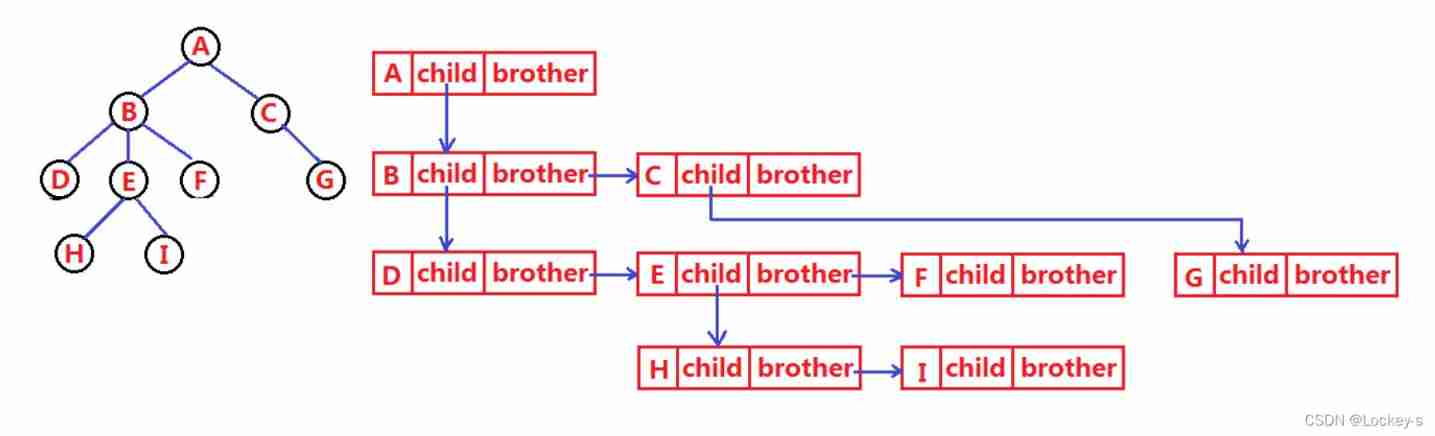

Binary tree

A binary tree consists of a root node plus two nodes, which are called Left subtree and right subtree Binary tree of ：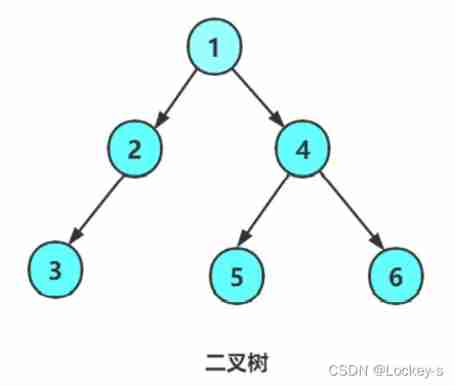

1. The degree of nonexistence of binary trees is greater than 2 The node of .
2. The subtree of a binary tree has left and right branches , The order cannot be reversed , So a binary tree is an ordered tree .

Composition of binary tree

The composition of binary tree is composed of the following ：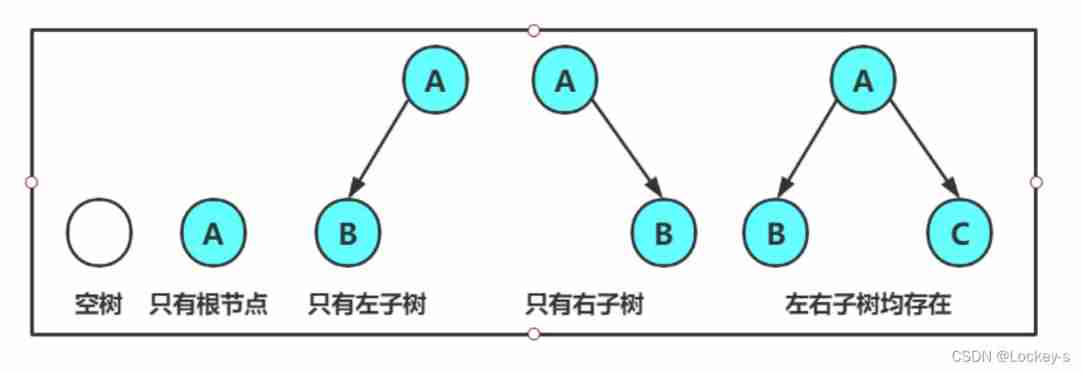

Two special binary trees

1. Full binary tree ： A binary tree , If the node number of each layer reaches the maximum , Then this binary tree is a full binary tree . in other words , If the number of layers of a binary tree is K, And the total number of nodes is , Then it's full of binary trees .
2. Perfect binary tree ： A complete binary tree is an efficient data structure , A complete binary tree is derived from a full binary tree . For a depth of K Of , Yes n A binary tree of nodes , If and only if each of its nodes has a depth of K From the full binary tree of 0 to n-1 A complete binary tree is called when its nodes correspond to each other . It should be noted that a full binary tree is a special kind of complete binary tree .
   

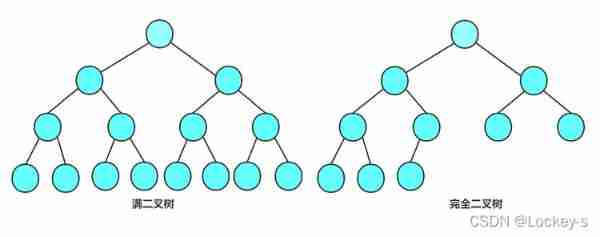
Properties of binary trees

1. If specified The number of layers of the root node is 1, Then a tree It's not the second of an empty binary tree i There is a maximum of (i>0) Nodes
2. If only The depth of the binary tree of the root node is 1, be Depth is K The number of nodes in a binary tree is the largest (k>=0)
3. Any binary tree , If it The number of leaf nodes is n0, Degree is 2 The number of non leaf nodes is n2, Then there are n0＝n2＋1
4. have n The depth of a complete binary tree of nodes k by Round up
5. Those who have n Complete binary tree of nodes , If according to From top to bottom, from left to right, for all nodes 0 Numbered starting , Then for the serial number is i There are ：

   if i>0, Parental serial number ：(i-1)/2;i=0,i Number the root node , No parent node
   if 2i+1<n, Left child serial number ：2i+1, Otherwise no left child
   if 2i+2<n, Right child number ：2i+2, Otherwise no right child

Binary tree storage

Binary tree storage includes sequential storage and chain storage . Here will be chain storage ： The chain storage of binary tree is referenced by nodes one by one , The common expressions are binary and trigeminal , As follows （ Child representation ）：

class Node {
    
	int val; //  Data fields 
	Node left; //  Left child's quote , It often represents the whole left sub tree rooted by the left child 
	Node right; //  Right child's quote , It often represents the whole right subtree with the right child as the root 
}

Realize binary tree

When it comes to implementation , It is created in an exhaustive way , It's not a real way to create a binary tree , I'll talk about it later , Here is to explain the function ：

Implementation class

Binary tree has value 、 Left the child 、 The right child . The definition is implemented in the class ：

class BTNode {
    
    public char val;
    public BTNode left;// Left child's quote 
    public BTNode right;// Right child's quote 
    public BTNode(char val) {
    
        this.val = val;
    }
}

Create trees

Define the root node of a binary tree , Then create... In an exhaustive way ：

public BTNode root;// The root node of a binary tree 
public BTNode creatTree() {
    
    BTNode A = new BTNode('A');
    BTNode B = new BTNode('B');
    BTNode C = new BTNode('C');
    BTNode D = new BTNode('D');
    BTNode E = new BTNode('E');
    BTNode F = new BTNode('F');
    BTNode G = new BTNode('G');
    BTNode H = new BTNode('H');
    A.left = B;
    A.right = C;
    B.left = D;
    B.right = E;
    C.left = F;
    C.right = G;
    E.right = H;
    return A;
}

Here is the will A As root node , Then modify the left and right pointing . Create such a binary tree ：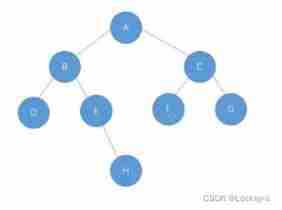

The former sequence traversal

The former sequence traversal （ It is also called pre root traversal ） When traversing a binary tree , First traverse the root , Then the left subtree , Finally, right subtree . Here's the picture ：

The preorder traversal of this binary tree is ：A B D E H C F G . So when traversing, recursively traverse in this way . The termination condition of recursive traversal is ： When the current node is empty , Just go back to . The code is as follows ：

void preOrder(BTNode root) {
    
    if (root == null) {
    
        return;
    }
    System.out.print(root.val+" ");
    preOrder(root.left);
    preOrder(root.right);
}

In the sequence traversal

In the sequence traversal （ Also called middle root traversal ） It's the first left subtree , Then there's the root , Finally, right subtree . As shown in the following figure, the result of the middle order traversal is ：D B E H A F C G

The code is as follows ：

void inOrder(BTNode root) {
    
    if (root == null) {
    
        return;
    }
    inOrder(root.left);
    System.out.print(root.val+" ");
    inOrder(root.right);
}

After the sequence traversal

After the sequence traversal （ Also called post root traversal ） Is the first left subtree , And then the right subtree , Finally, the root , As shown in the following figure, the result of post order traversal is ：D H E B F G C A

The code is as follows ：

void postOrder(BTNode root) {
    
    if (root == null) {
    
        return;
    }
    postOrder(root.left);
    postOrder(root.right);
    System.out.print(root.val+" ");
}

Get the number of nodes in the binary tree

There are two ways to get the number of nodes in a binary tree ：1、 Traversal methods ,2、 Sub problem method （ The number of nodes of the left tree + The number of nodes of the right tree .

Traversal methods

You can traverse through a traversal method , Then define a counter , Used to calculate the number . The code is as follows ：

int count = 0;
int size(BTNode root) {
    
    if (root == null) {
    
        return 0;
    }
    count++;
    size(root.left);
    size(root.right);
    return count;
}

Sub problem method

By judging the number of left subtrees and right subtrees . The code is as follows ：

int size1(BTNode root) {
    
    if (root == null) {
    
        return 0;
    }
    return size1(root.left) + size1(root.right) + 1;
}

Get the number of leaf nodes

There are also two methods to obtain here ：1、 Traversal ideas 2、 Sub problem ideas

Traversal methods

If you traverse to the leaf node , The counter is just ++, The leaf node is left and right All is empty . The code is as follows ：

int num = 0;
int getLeafNodeCount(BTNode root) {
    
    if (root == null) {
    
        return 0;
    }
    if (root.left == null && root.right == null) {
    
        num++;
    }
    getLeafNodeCount(root.left);
    getLeafNodeCount(root.right);
    return num;
}

Sub problem method

The sub problem method here is the leaves of the left tree + The leaves of the right tree , If it's a leaf , Just go back to 1 The code is as follows ：

int getLeafNodeCount1(BTNode root) {
    
    if (root == null) {
    
        return 0;
    }
    if (root.left == null && root.right == null) {
    
        return 1;
    }
    return getLeafNodeCount1(root.left) + getLeafNodeCount1(root.right);
}

Please k The number of layer nodes

Please k layer , That is, every lower layer , Give Way k - 1 When k == 1 When , That's it k The layer , As shown in the figure ：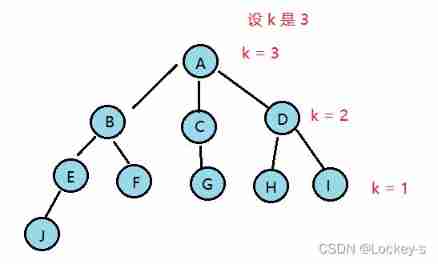

So when recursive to k == 1 When , return 1 That's all right. . The code is as follows ：

int getKLevelNodeCount(BTNode root, int k) {
    
    if (root == null) {
    
        return 0;
    }
    if (k == 1) {
    
        return 1;
    }
    return getKLevelNodeCount(root.left, k - 1) + getKLevelNodeCount(root.right, k - 1);
}

Get the height of the binary tree

The height of the left tree and the height of the right tree are also compared recursively to maximize , Then when you return + 1 . Here's the picture ：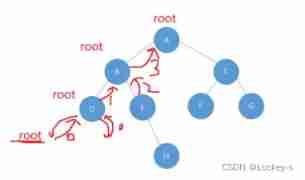

The code is as follows ：

int getHeight(BTNode root) {
    
    if (root == null) {
    
        return 0;
    }
    if (root.left == null && root.right == null) {
    
        return 1;
    }
    return Math.max(getHeight(root.left), getHeight(root.right)) + 1;
}

The detected value is value Does the element of exist

To detect whether this element exists , Then directly traverse whether the node has value The data is enough . If not found, return null , The code is as follows ：

BTNode find(BTNode root, char val) {
    
    if (root == null) {
    
        return null;
    }
    if (root.val == val) {
    
        return root;
    }
    BTNode ret = find(root.left, val);
    if (ret != null) {
    
        return ret;
    }
    return find(root.right, val);
}

Judge whether a tree is a complete binary tree

You can use queues , Put every node in the queue , Even if it is null Also put . After putting it in , Pop team leader element , Then put the left and right of the pop-up team head element into . If it comes out null When , All that's left is null , So it's a complete binary tree . The code is as follows ：

boolean isCompleteTree(BTNode root) {
    
    if (root == null) {
    
        return true;
    }
    Queue<BTNode> queue = new LinkedList<>();
    queue.offer(root);
    while (!queue.isEmpty()) {
    
        BTNode cur = queue.poll();
        if (cur != null) {
    
            queue.offer(cur.left);
            queue.offer(cur.right);
        } else {
    
            break;
        }
    }
    while (!queue.isEmpty()) {
    
        BTNode top = queue.peek();
        if (top != null) {
    
            return false;
        }
        queue.poll();
    }
    return true;
}

Sequence traversal

The sequence traversal here is also implemented by queues , It is almost the same as the above judgment whether it is a complete binary tree , It's just time to get out of the team , Judge that the node is not empty , Then you can join the team if the left and right nodes are not empty , Until the last queue is empty . The code is as follows ：

public void levelOrder(BTNode root) {
    
    Queue<BTNode> queue = new LinkedList<>();
    if (root == null) {
    
        return;
    }
    queue.offer(root);
    while (!queue.isEmpty()) {
    
        BTNode cur = queue.poll();
        System.out.print(cur.val+" ");
        if (cur != null) {
    
            if (cur.left != null) {
    
                queue.offer(cur.left);
            }
            if (cur.right != null) {
    
                queue.offer(cur.right);
            }
        }
    }
}

Find the nearest common ancestor

Find the common ancestor of two nodes , Suppose it is a binary search tree . The size of the middle order traversal of the binary search tree is ordered . The left number of the root node , Smaller than root . Right tree of root node , Are bigger than root . So the situation shown in the figure below will appear ：

therefore , We just need to follow this pattern , If neither the left nor the right is empty , It means that these two nodes are on both sides of the root node , Just return to the root node directly . Then, if the left side is not empty , Just go back to the left . The right side is not empty , Just go back to the right . The code is as follows ：

public BTNode lowestCommonAncestor(BTNode root, TreeNode p, TreeNode q) {
    
    if(root == null) {
    
        return null;
    }
    if(root == p || root == q) {
    
        return root;
    }
    BTNode left = lowestCommonAncestor(root.left, p, q);
    BTNode right = lowestCommonAncestor(root.right, p, q);
    if(left != null && right != null) {
    
        return root;
    } else if (left != null) {
    
        return left;
    } else {
    
        return right;
    }
}

Code testing

The code is as follows ：

public static void main(String[] args) {
    
    MyBinaryTree myBinaryTree = new MyBinaryTree();
    BTNode root = myBinaryTree.creatTree();
    System.out.println(" The former sequence traversal ");
    myBinaryTree.preOrder(root);
    System.out.println();
    System.out.println(" In the sequence traversal ");
    myBinaryTree.inOrder(root);
    System.out.println();
    System.out.println(" After the sequence traversal ");
    myBinaryTree.postOrder(root);
    System.out.println();
    System.out.println(" The number of nodes in a binary tree ");
    System.out.println(myBinaryTree.size1(root));
    System.out.println(" The number of leaf nodes in a binary tree ");
    System.out.println(myBinaryTree.getLeafNodeCount1(root));
    System.out.println(" The second in the binary tree  k  The number of layer nodes ");
    System.out.println(myBinaryTree.getKLevelNodeCount(root, 3));
    System.out.println(" The number of highly ");
    System.out.println(myBinaryTree.getHeight(root));
    System.out.println(" Include this node , Included words , Output this node ");
    try {
    
        System.out.println(myBinaryTree.find(root, 'G').val);
    } catch (NullPointerException e) {
    
        e.printStackTrace();
        System.out.println(" Without this node ");
    }
    System.out.println(" Is it a complete binary tree ");
    System.out.println(myBinaryTree.isCompleteTree(root));
    System.out.println(" Sequence traversal ");
    myBinaryTree.levelOrder(root);
}

The operation results are as follows ：