当前位置:网站首页>Différences entre les contraintes monotones et anti - monotones
Différences entre les contraintes monotones et anti - monotones
2022-07-07 10:40:00 【Xminyang】
▚ 01 Monotone Constraints Contraintes monotones
1.1 Definitions Définition
【Monotone Constraints | SpringerLink 】
A constraint C is monotone if and only if for all itemsets S and S′:
if S ⊇ S′ and S violates C, then S′ violates C.
1.2 Key Points Points saillants
Monotone constraints possess the following property. If an itemset S violates a monotone constraint C, then any of its subsets also violates C. Equivalently, all supersets of an itemset satisfying a monotone constraint C also satisfy C (i.e., C is upward closed). By exploiting this property, monotone constraints can be used for reducing computation in frequent itemset mining with constraints. As frequent itemset mining with constraints aims to find frequent itemsets that satisfy the constraints, if an itemset S satisfies a monotone constraint C, no further constraint checking needs to be applied to any superset of S because all supersets of S are guaranteed to satisfy C. Examples of monotone constraints include min(S. Price) ≤ $30, which expresses that the minimum price of all items in an itemset S is at most $30. Note that, if the minimum price of all items in S is at most $30, adding more items to S would not increase its minimum price (i.e., supersets of S would also satisfy such a monotone constraint).

▚ 02 Anti-monotone Constraints Contrainte anti - monotone
2.1 Definitions Définition
【Anti-monotone Constraints | SpringerLink】
A constraint C is anti-monotone if and only if for all itemsets S and S′:
if S ⊇ S′and S satisfies C, then S′ satisfies C.
2.2 Key Points Points saillants
Anti-monotone constraints possess the following nice property. If an itemset S satisfies an anti-monotone constraint C, then all of its subsets also satisfy C (i.e., C is downward closed). Equivalently, any superset of an itemset violating an anti-monotone constraint C also violates C. By exploiting this property, anti-monotone constraints can be used for pruning in frequent itemset mining with constraints. As frequent itemset mining with constraints aims to find itemsets that are frequent and satisfy the constraints, if an itemset violates an anti-monotone constraint C, all its supersets (which would also violate C) can be pruned away and their frequencies do not need to be counted. Examples of anti-monotone constraints include min(S. Price) ≥ $20 (which expresses that the minimum price of all items in an itemset S is at least $20) and the usual frequency constraint support(S) ≥ minsup (i.e., frequency(S) ≥ minsup). For the former, if the minimum price of all items in S is less than $20, adding more items to S would not increase its minimum price (i.e., supersets of S would not satisfy such an anti-monotone constraint). For the latter, it is widely used in frequent itemset mining, with or without constraints. It states that (i) all subsets of a frequent itemset are frequent and (ii) any superset of an infrequent itemset is also infrequent. This is also known as the Apriori property.

▚ 03 Explanation Explication
Hypothèses:On vaS violates CEn tant qu'événementA,S′ violates CEn tant qu'événementB;Et S satisfies CPour l'événementnot A,then S′ satisfies CPour l'événementnot B.
En ce moment,SelonMonotone Constraints Définition (A → B),C'est - à - dire(not B → not A);
SelonAnti-monotonicity Constraints Définition (not A → not B),C'est - à - dire(B → A);
Parce que(A → B)Cela ne signifie pas nécessairement(B → A), Donc les deux (Monotone Constraints & Anti-monotonicity Constraints) La déclaration est différente .

▚ 04 Example Exemple
For an example. Consider-
C1 = Sum of elements is greater than 5
C2 = Sum of elements is at most 5
U(universe) = Set of non-negative real numbers
In case of C1,
If S violates C1, then S’ obviously violates C1 as well (S being a superset of S’)
Eg. S = {1, 2}, S’ = {2}
Hence C1 is monotonic.
In case of C2,
If S satisfies C2, then S’ obviously satisfies C2 as well (S being a superset of S’)
Eg. S = {1, 2}, S’ = {2}
Hence C2 is anti-monotonic.

▚ 05 Contraintes de l'exploration des données
Constraint-Based Mining — A General Picture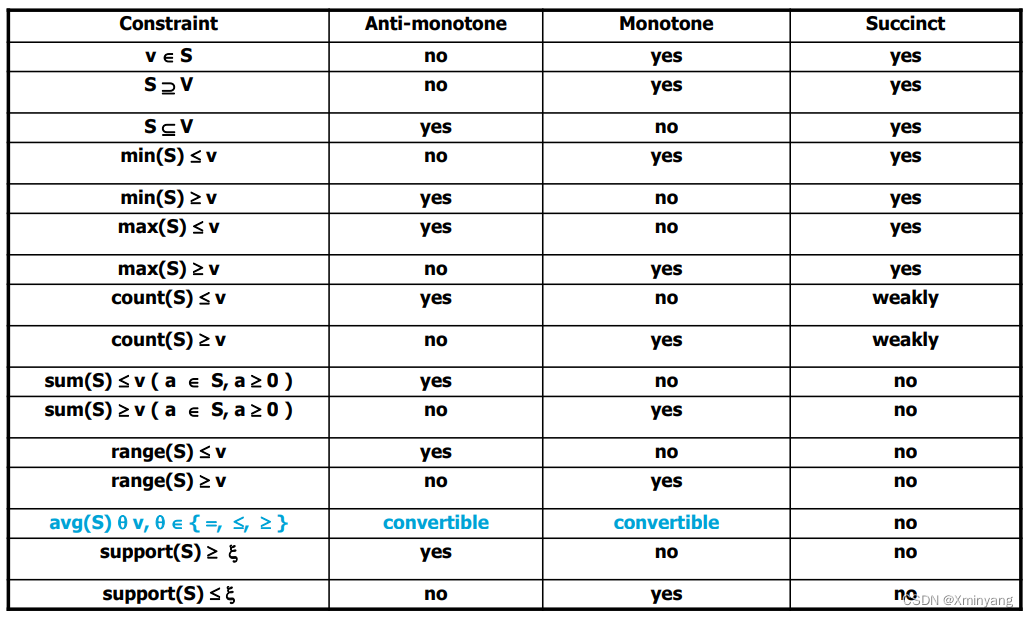

Article de référence
边栏推荐
- SQL Server 知识汇集11 : 约束
- 软考中级有用吗??
- Prototype and prototype chain
- 1324:【例6.6】整数区间
- TypeScript 接口继承
- 多线程-异步编排
- 长列表性能优化方案 memo
- openinstall与虎扑达成合作,挖掘体育文化产业数据价值
- Mendeley -- a free document management tool that automatically inserts references into papers
- The mobile terminal automatically adjusts the page content and font size by setting rem
猜你喜欢
What are the test preparation materials and methods for soft exam information processing technicians?
MONAI版本更新到 0.9 啦,看看有什么新功能
![[recommendation system 02] deepfm, youtubednn, DSSM, MMOE](/img/d5/33765983e6b98235ca085f503a1272.png)
[recommendation system 02] deepfm, youtubednn, DSSM, MMOE
Use the fetch statement to obtain the repetition of the last row of cursor data

CAS mechanism
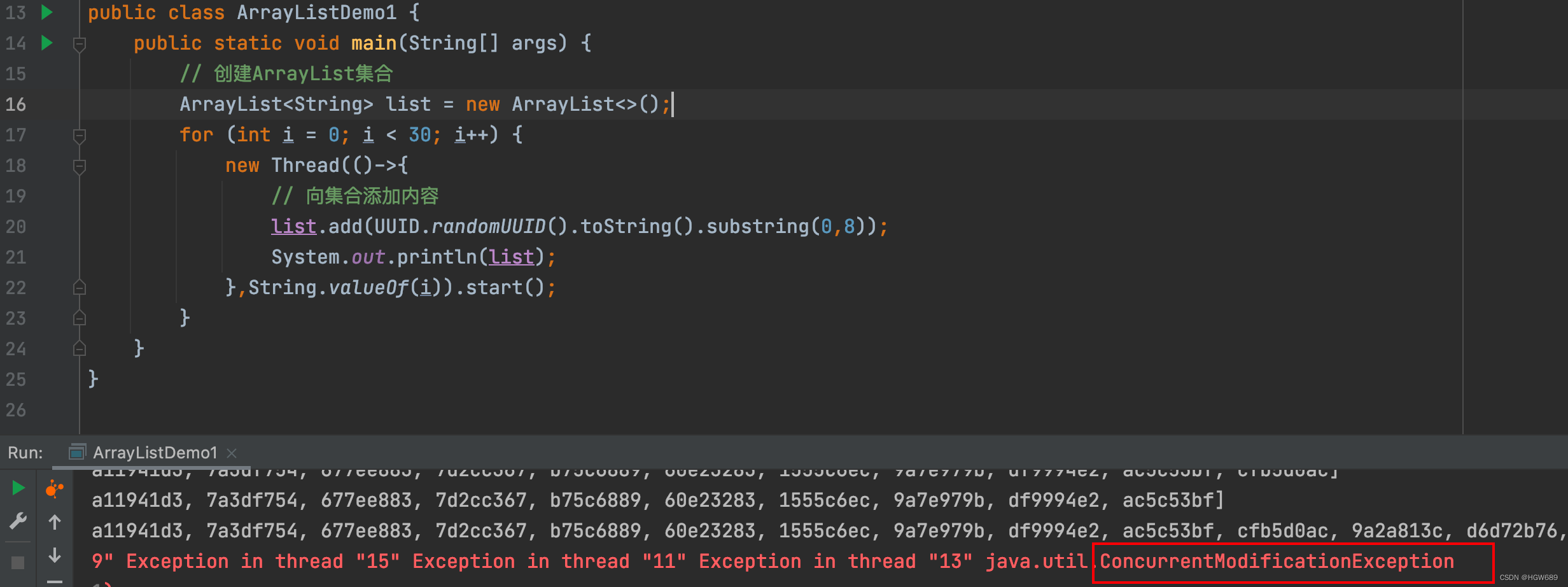
ArrayList线程不安全和解决方案
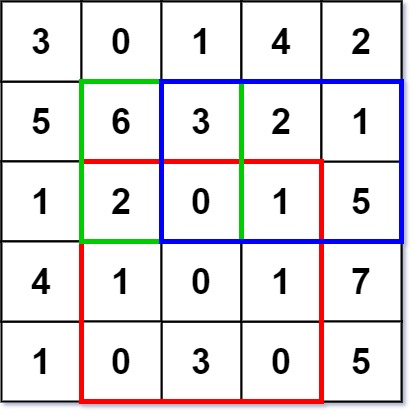
leetcode-304:二维区域和检索 - 矩阵不可变

CAS机制
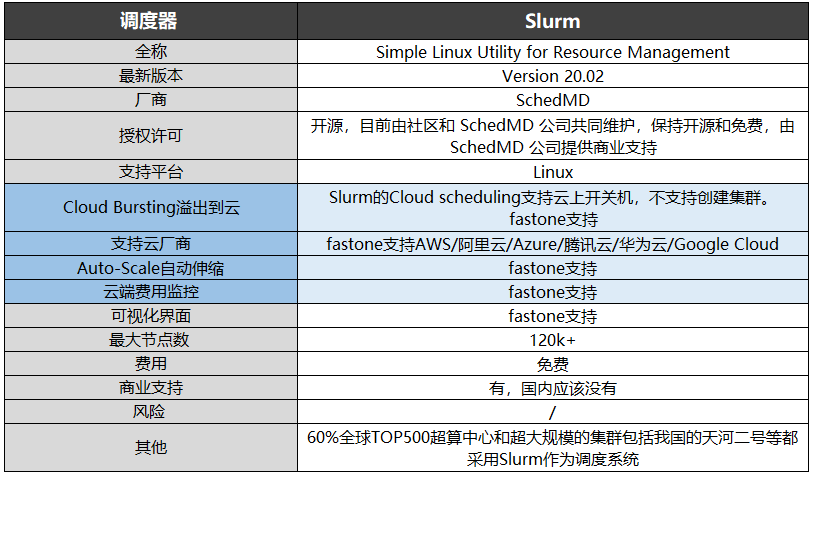
Cluster task scheduling system lsf/sge/slurm/pbs based on HPC scenario
![[système recommandé 01] rechub](/img/92/c14c867247d3a042c69b5ed0091fbe.png)
[système recommandé 01] rechub
随机推荐
原型与原型链
ThreadLocal is not enough
Cluster task scheduling system lsf/sge/slurm/pbs based on HPC scenario
What are the test preparation materials and methods for soft exam information processing technicians?
施努卡:机器视觉定位技术 机器视觉定位原理
Gym installation pit records
宁愿把简单的问题说一百遍,也不把复杂的问题做一遍
CSAPP Bomb Lab 解析
P2788 数学1(math1)- 加减算式
I'd rather say simple problems a hundred times than do complex problems once
Trajectory planning for multi robot systems: methods and Applications Overview reading notes
Common shortcut keys in IDA
Using U2 net deep network to realize -- certificate photo generation program
求方程ax^2+bx+c=0的根(C语言)
【推薦系統 01】Rechub
How to prepare for the advanced soft test (network planning designer)?
Use the fetch statement to obtain the repetition of the last row of cursor data
Using tansformer to segment three-dimensional abdominal multiple organs -- actual battle of unetr
软考中级,软件设计师考试那些内容,考试大纲什么的?
Jump to the mobile terminal page or PC terminal page according to the device information