当前位置:网站首页>2022/7/1学习总结
2022/7/1学习总结
2022-07-05 04:55:00 【ls真的不会啊】
一、102. 二叉树的层序遍历 - 力扣(LeetCode)
题目描述
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:输入:root = [1]
输出:[[1]]
示例 3:输入:root = []
输出:[]
提示:
树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000
思路
层序遍历过程,其实就是从上到下,从左到右依次将每个数放入到队列中,然后按顺序依次打印就是想要的结果。
代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> a;
queue<TreeNode*> q;
if(root!=NULL)//根结点
{
q.push(root);
}
while(!q.empty())
{
vector<int> b;
int size=q.size();
while(size--)
{
//遍历完该结点的左右子结点的时候,就将该结点出队列
if(q.front()->left)
{
q.push(q.front()->left);
}
if(q.front()->right)
{
q.push(q.front()->right);
}
b.push_back(q.front()->val);
q.pop();
}
a.push_back(b);
}
return a;
}
};二、20. 有效的括号 - 力扣(LeetCode)
题目描述
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
示例 1:
输入:s = "()"
输出:true
示例 2:输入:s = "()[]{}"
输出:true
示例 3:输入:s = "(]"
输出:false
示例 4:输入:s = "([)]"
输出:false
示例 5:输入:s = "{[]}"
输出:true
提示:
1 <= s.length <= 104
s 仅由括号 '()[]{}' 组成
思路
这就是一个简单的关于栈的题目。如果遇到左半边括号,就入栈。如果遇到右半边括号,就拿栈顶元素和它比较,如果两者匹配的话,就出栈,否则,字符串无效。如果前面这一步没有出问题,就最后检查一下栈是否为空,如果非空,那字符串无效。
代码实现
class Solution {
public:
bool isValid(string s) {
char a[10001];
int top=0;
for(int i=0;i<s.length();i++)
{
if(s[i]=='('||s[i]=='['||s[i]=='{')
{
a[top++]=s[i];
}
else
{
if(s[i]==')')
{
if(top>0&&a[top-1]=='(')
{
top--;
}
else
{
return false;
}
}
if(s[i]=='}')
{
if(top>0&&a[top-1]=='{')
{
top--;
}
else
{
return false;
}
}
if(s[i]==']')
{
if(top>0&&a[top-1]=='[')
{
top--;
}
else
{
return false;
}
}
}
}
if(top==0)
{
return true;
}
else
{
return false;
}
}
};三、121. 买卖股票的最佳时机 - 力扣(LeetCode)
题目描述
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 105
0 <= prices[i] <= 104
思路
因为如果没有合适的价格,则不进行交易,利润为0,所以以卖出日期为准,找卖出日期之前的最小买入价格,从而找到每个卖出日期能获得的最大利润。
代码实现
class Solution {
public:
int maxProfit(vector<int>& prices) {
int max,min=prices[0],dp[prices.size()];
dp[0]=0;
max=dp[0];
for(int i=1;i<prices.size();i++)
{
if(prices[i]<min)//该日之前的最小的买入价格
{
min=prices[i];
}
dp[i]=prices[i]-min;
if(max<dp[i])
{
max=dp[i];
}
}
return max;
}
};边栏推荐
- Redis has four methods for checking big keys, which are necessary for optimization
- The principle of attention mechanism and its application in seq2seq (bahadanau attention)
- 中国溶聚丁苯橡胶(SSBR)行业研究与预测报告(2022版)
- [Business Research Report] top ten trends of science and technology and it in 2022 - with download link
- Leetcode word search (backtracking method)
- [groovy] closure (closure parameter list rule | default parameter list | do not receive parameters | receive custom parameters)
- #775 Div.1 C. Tyler and Strings 组合数学
- 2021 electrician Cup - high speed rail traction power supply system operation data analysis and equivalent modeling ideas + code
- The difference between heap and stack
- SQLServer 存储过程传递数组参数
猜你喜欢
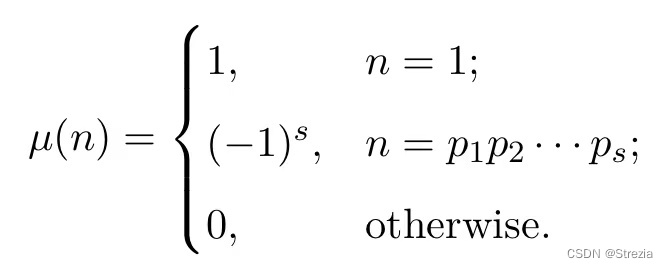
Number theoretic function and its summation to be updated
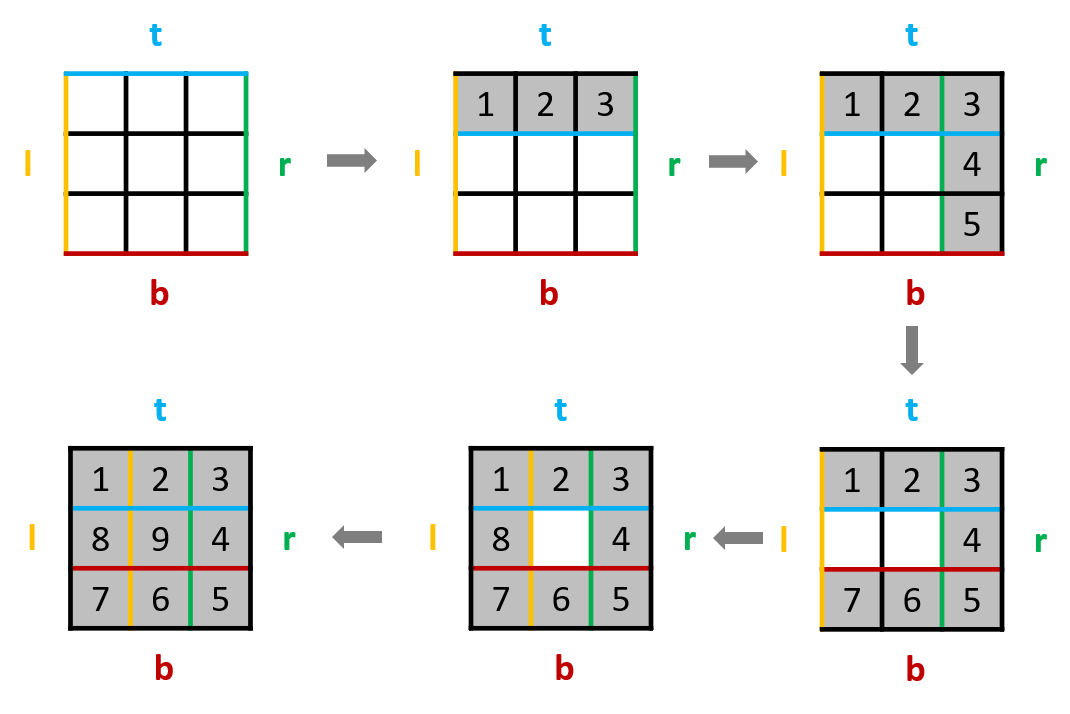
54. 螺旋矩阵 & 59. 螺旋矩阵 II ●●

Leetcode word search (backtracking method)

次小生成树
![[groovy] closure (Introduction to closure class closure | closure parametertypes and maximumnumberofparameters member usage)](/img/1b/1fa2ebc9a6c5d271c9b39f5e508fb0.jpg)
[groovy] closure (Introduction to closure class closure | closure parametertypes and maximumnumberofparameters member usage)
【acwing】528. cheese

Solution of circular dependency

【acwing】836. Merge sets

AutoCAD - set layer
![Rip notes [rip message security authentication, increase of rip interface measurement]](/img/89/f70af97676496d7b9aa867be89f11d.jpg)
Rip notes [rip message security authentication, increase of rip interface measurement]
随机推荐
The 22nd Spring Festival Gala, an immersive stage for the yuan universe to shine into reality
[Chongqing Guangdong education] National Open University 2047t commercial bank operation and management reference test in autumn 2018
Pdf to DWG in CAD
Rip notes [rip message security authentication, increase of rip interface measurement]
AutoCAD - set layer
2022 American College Students' mathematical modeling ABCDEF problem thinking /2022 American match ABCDEF problem analysis
Redis 排查大 key 的4种方法,优化必备
JMeter -- distributed pressure measurement
Wan broadband access technology V EPON Technology
MD5 bypass
Rip notes [rip three timers, the role of horizontal segmentation, rip automatic summary, and the role of network]
Research and investment forecast report of adamantane industry in China (2022 Edition)
jmeter -- 分布式压测
MySQL audit log archiving
2022 U.S. college students' mathematical modeling e problem ideas / 2022 U.S. game e problem analysis
2022 thinking of Mathematical Modeling B problem of American college students / analysis of 2022 American competition B problem
Basic knowledge points
The principle of attention mechanism and its application in seq2seq (bahadanau attention)
Create a pyGame window with a blue background
質量體系建設之路的分分合合