当前位置:网站首页>LeetCode 1545. Find the k-th bit in the nth binary string
LeetCode 1545. Find the k-th bit in the nth binary string
2022-07-06 16:42:00 【Daylight629】
1545. Find out the N Of the binary strings K position
Here are two positive integers n and k, Binary string Sn The formation rules of are as follows :
S1 = "0"- When
i > 1when ,Si = Si-1 + "1" + reverse(invert(Si-1))
among + Indicates series operation ,reverse(x) Return to reverse x The resulting string , and invert(x) Will flip x Every one of you (0 Turn into 1, and 1 Turn into 0).
for example , The first of the sequences described above 4 The strings are :
S1 = "0"S2 = "0**1**1"S3 = "011**1**001"S4 = "0111001**1**0110001"
Please return Sn Of The first k Bit character , Topic data assurance k It must be Sn Within the length range .
Example 1:
Input :n = 3, k = 1
Output :"0"
explain :S3 by "0111001", Its first 1 Position as "0" .
Example 2:
Input :n = 4, k = 11
Output :"1"
explain :S4 by "011100110110001", Its first 11 Position as "1" .
Example 3:
Input :n = 1, k = 1
Output :"0"
Example 4:
Input :n = 2, k = 3
Output :"1"
Tips :
1 <= n <= 201 <= k <= 2n - 1
Two 、 Method 1
recursive
class Solution {
public char findKthBit(int n, int k) {
if (k == 1) {
return '0';
}
int mid = 1 << (n - 1);
if (k == mid) {
return '1';
} else if (k < mid) {
return findKthBit(n - 1, k);
} else {
k = mid * 2 - k;
return invert(findKthBit(n - 1, k));
}
}
public char invert(char a) {
return (char) ('0' + '1' - a);
}
}
Complexity analysis
Time complexity :O(n). character string S_n The length of is 2^n-1, Each recursive call can reduce the search range by half , So the time complexity is zero O(log2n)=O(n).
Spatial complexity :O(n). The space complexity mainly depends on the stack space generated by recursive calls , The number of recursive call layers will not exceed n.
边栏推荐
- Hbuilder X格式化快捷键设置
- Classic application of stack -- bracket matching problem
- 新手必会的静态站点生成器——Gridsome
- Raspberry pie 4B installation opencv3.4.0
- Kubernetes集群部署
- Spark的RDD(弹性分布式数据集)返回大结果集
- Spark独立集群Worker和Executor的概念
- China double brightening film (dbef) market trend report, technical dynamic innovation and market forecast
- Investigation report of bench type Brinell hardness tester industry - market status analysis and development prospect prediction
- Codeforces Round #797 (Div. 3)无F
猜你喜欢
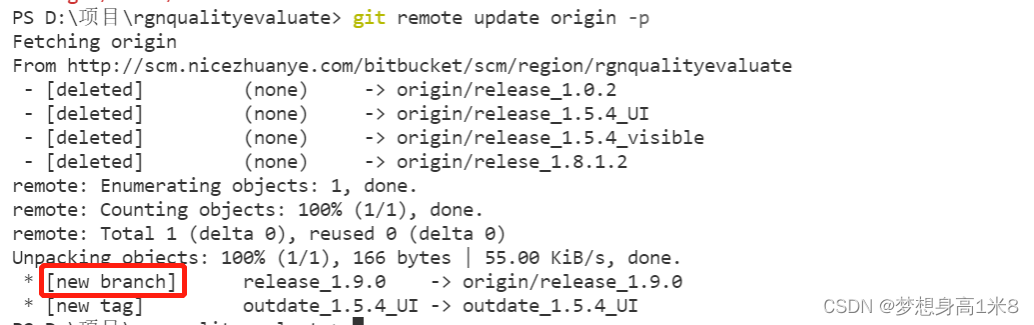
Pull branch failed, fatal: 'origin/xxx' is not a commit and a branch 'xxx' cannot be created from it

业务系统兼容数据库Oracle/PostgreSQL(openGauss)/MySQL的琐事
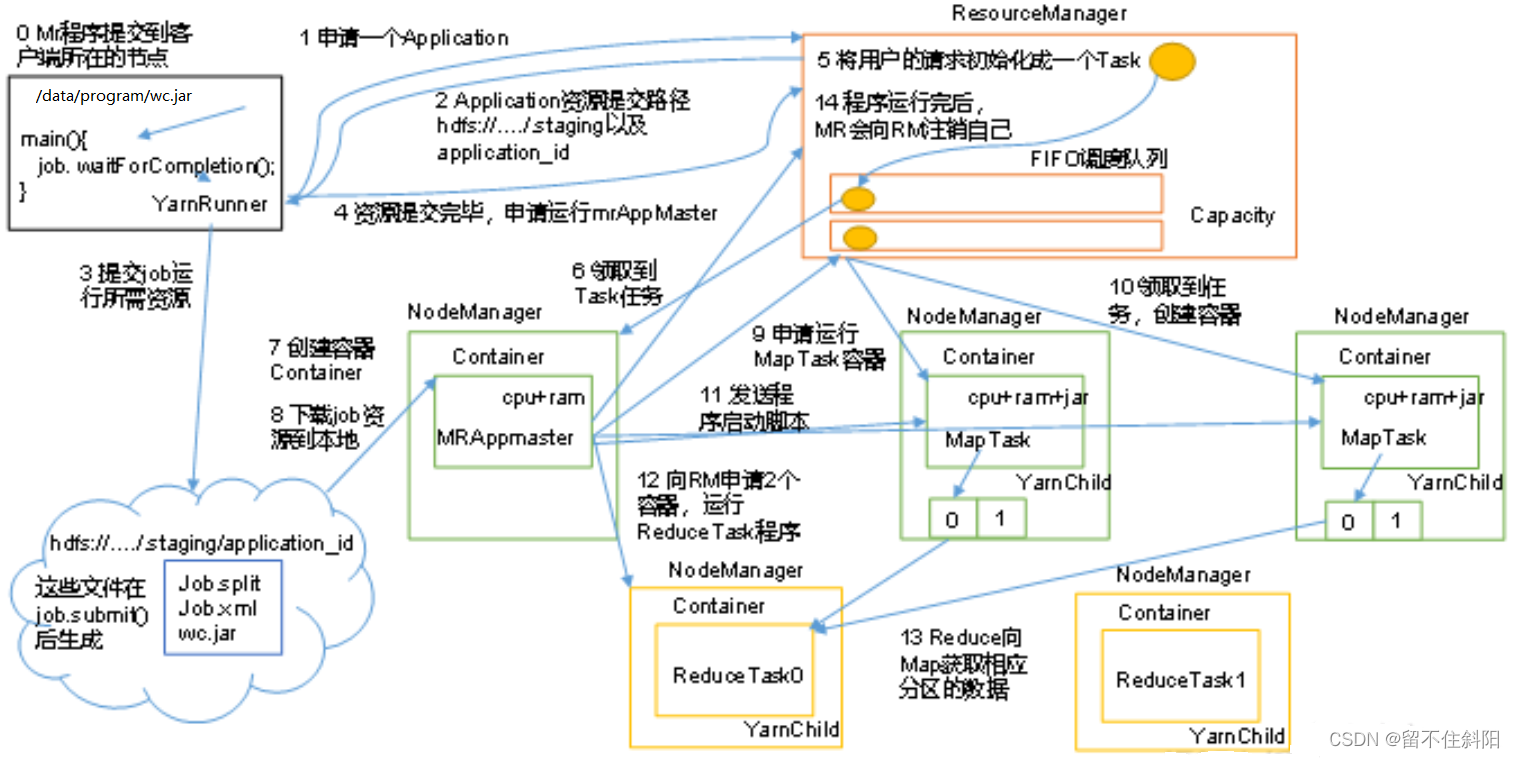
第五章 Yarn资源调度器
本地可视化工具连接阿里云centOS服务器的redis
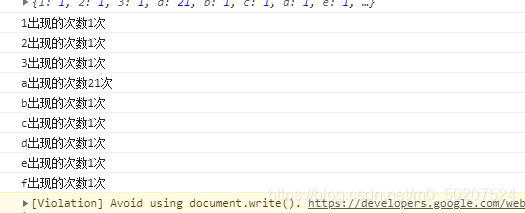
软通乐学-js求字符串中字符串当中那个字符出现的次数多 -冯浩的博客

字节跳动新程序员成长秘诀:那些闪闪发光的宝藏mentor们
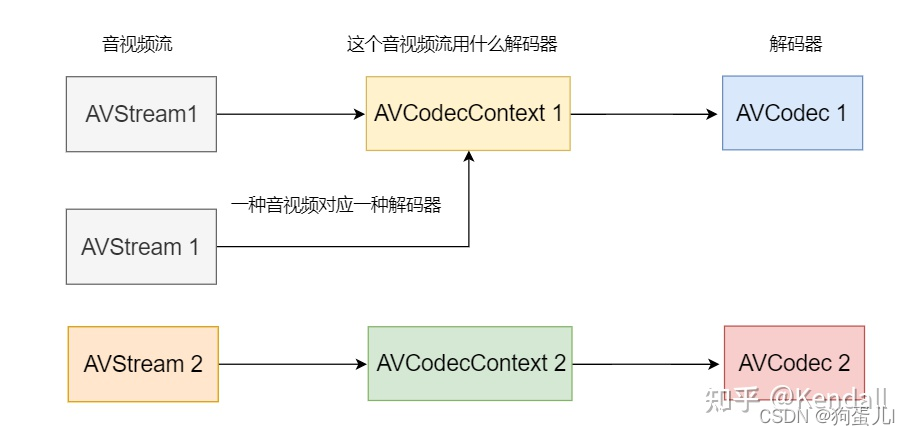
音视频开发面试题
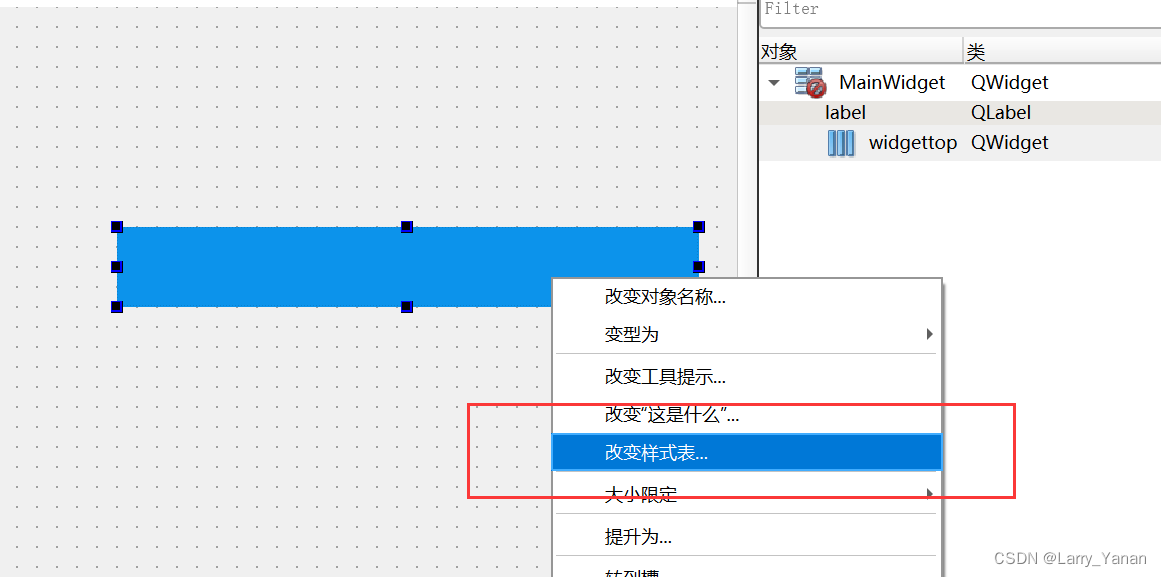
Discussion on QWidget code setting style sheet
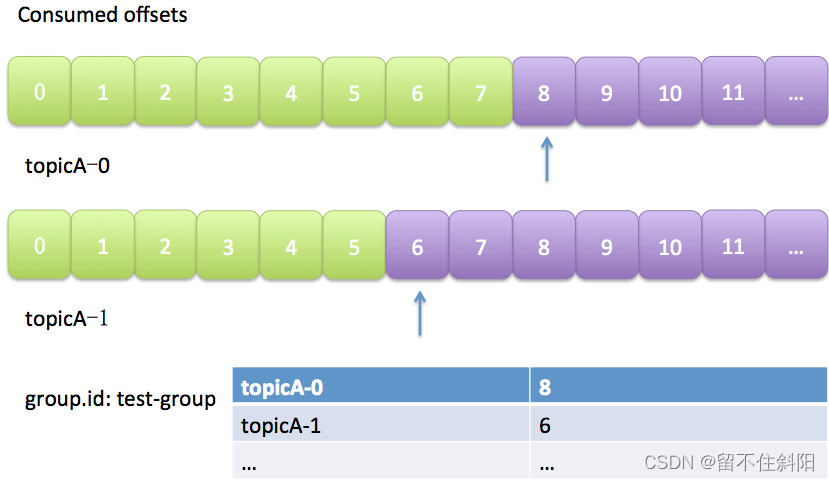
Chapter 5 detailed explanation of consumer groups
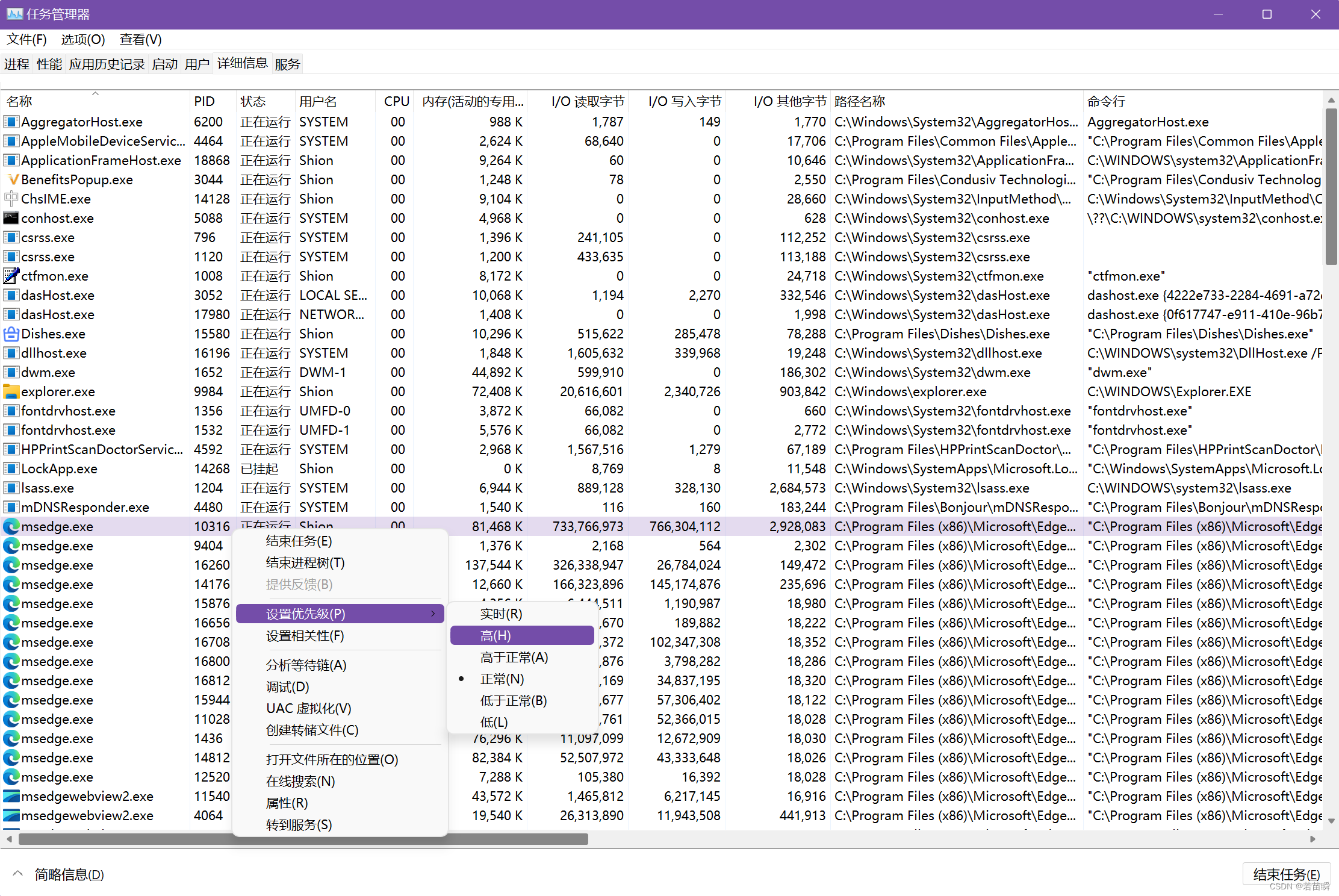
解决Intel12代酷睿CPU单线程调度问题(二)
随机推荐
FLV格式详解
(POJ - 1458) common subsequence (longest common subsequence)
(lightoj - 1369) answering queries (thinking)
浏览器打印边距,默认/无边距,占满1页A4
Native JS realizes the functions of all selection and inverse selection -- Feng Hao's blog
The concept of spark independent cluster worker and executor
MariaDB的安装与配置
QT style settings of qcobobox controls (rounded corners, drop-down boxes, up expansion, editable, internal layout, etc.)
Spark's RDD (elastic distributed data set) returns a large result set
第五章 Yarn资源调度器
Simple records of business system migration from Oracle to opengauss database
Research Report on market supply and demand and strategy of Chinese table lamp industry
Li Kou - 298th weekly match
Chapter III principles of MapReduce framework
Problem - 1646C. Factorials and Powers of Two - Codeforces
(lightoj - 1236) pairs forming LCM (prime unique decomposition theorem)
JS time function Daquan detailed explanation ----- AHAO blog
Market trend report, technological innovation and market forecast of desktop electric tools in China
Advancedinstaller installation package custom action open file
使用jq实现全选 反选 和全不选-冯浩的博客