Dynamic planning idea "from getting started to giving up"

Definition of dynamic programming

Break up the original problem into several sub problems , At the same time, save the answers to the sub questions , So that each subproblem can be solved only once , Finally get the answer to the original question .

The general process of Dynamic Planning

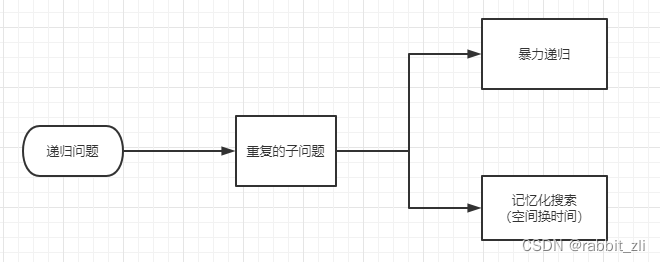
Example 1： Dynamic programming of one-dimensional space

subject ： Find the Fibonacci sequence

• Violent recursive solution

//  Use recursion to solve 
int fibonacci(int i) {
    
	return i <= 1 : i : fibonacci(i - 1) + fibonacci(i - 2);
}

The time complexity of violent recursion is exponential , We need to use memory search to solve this problem

• Memory search （ Dynamic planning ideas ）

//  Using the idea of dynamic planning   Memory search 
int fibonacci(int fib) {
    
	//  Define an array   Store the N Fibonacci number of items 
    int[] cache = new int[fib + 1];
    //  Traverse 
    for (int i = 0; i < cache.length; i++) {
    
        if (fib <= 1) {
    
            cache[i] = i;
            continue;
        }
        cache[i] = cache[i - 2] + cache[i - 1];
    }
    return cache[fib];
}

Complex dynamic programming

Complex dynamic programming ：

1. Dimensions have changed It may be two-dimensional or three-dimensional space ;
2. There may be a trade-off optimal substructure in the middle

subject 2： Different paths
Title Description ： A robot is in a m x n The top left corner of the grid （ The starting point is marked as “Start” ）.
The robot can only move down or right one step at a time . The robot tries to reach the bottom right corner of the grid （ In the figure below, it is marked as “Finish” ）.
Ask how many different paths there are in total ？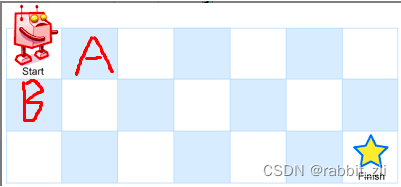

For the above questions , Because you can only Right or down go , So we can turn it into a sub problem ：
Sub problem 1： about A How to get to the lower right corner
Sub problem 2： about B How to get to the lower right corner
So the total walking method is equal to 【A】 The solution of the subproblem ＋【B】 The solution of the subproblem

• Solution 1 ： Use the conventional recursive solution

//  Using recursive solutions 
int paths(int m, int n) {
    
	//  Define a two-dimensional mesh 
	int[][] table = new int[m][n];
	//  Call recursive functions 
	return dfs(table, 0, 0);
}
int dfs(int[][] table, int row, int col) {
    
	//  Recursive termination condition 
	// 1.1  Dealing with boundary values 
	if (row < 0 || row >= table.length || col < 0 || col >= table[0].length) {
    
		return 0;
	}
	// 1.2  If you go to your destination   Then return to 1
	if (row == table.length - 1 && col == table[0].length - 1) {
    
		return 1;
	}
	//  Transform into the solution of the subproblem 
	return dfs(table, row + 1, col) + dfs(table, row, col + 1);
}

• Solution 2 ： Memory search

/**  Use the idea of dynamic programming to solve   You can find   The number of paths in each grid is determined by the total number of paths in the upper grid and the left grid  */
int paths(int m, int n) {
    
	//  Define a two-dimensional matrix 
	int[][] table = new table[m][n];
	//  First initialize the first row and first column 
	for (int i = 0; i < m; i++) {
    
		table[m][0] = 1;
	}
	for (int i = 0; i < n; i++) {
    
		table[0][n] = 1;
	}
	for (int i = 1; i < m; i++) {
    
		for (int j = 1; j < n; j++) {
    
			table[i][j] = table[i - 1][j] + table[i][j - 1];
		}
	}
	return table[m - 1][n - 1];
}