当前位置:网站首页>20220701 Barbalat引理证明
20220701 Barbalat引理证明
2022-07-04 08:47:00 【能吃辣吗】
(Barbalat 引理)
如果可微函数 f ( t ) f(t) f(t), 当 t → ∞ t \rightarrow \infty t→∞ 时存在有限极限, 且 f ˙ ( t ) \dot{f}(t) f˙(t) 一致连续, 那么当 t → ∞ t \rightarrow \infty t→∞ 时, f ˙ ( t ) → 0 \dot{f}(t) \rightarrow 0 f˙(t)→0。
证明(反证法):
假设当 t → ∞ t \rightarrow \infty t→∞ 时, f ˙ ( t ) → 0 \dot{f}(t) \rightarrow 0 f˙(t)→0 不成立,那么存在一个递增无穷序列 { t n } n ∈ N \{t_n\}_{n\in\mathbb{N}} { tn}n∈N 使得(1)当 n → ∞ n \rightarrow \infty n→∞ 有 t n → ∞ t_n \rightarrow \infty tn→∞ ;(2) ∣ f ˙ ( t n ) ∣ ⩾ ϵ > 0 |\dot{f}(t_n) | \geqslant \epsilon>0 ∣f˙(tn)∣⩾ϵ>0 对于所有 { t n } \{t_n\} { tn}。
考虑 f ˙ ( t ) \dot{f}(t) f˙(t) 的一致连续性,根据 ϵ − δ \epsilon-\delta ϵ−δ 理论,存在某个 ϵ > 0 \epsilon>0 ϵ>0 ,使得对于所有 n ∈ N n\in\mathbb{N} n∈N 和 所有 t ∈ R t \in \mathbb{R} t∈R,当
∣ t n − t ∣ ⩽ δ |t_n -t|\leqslant\delta ∣tn−t∣⩽δ则有 ∣ f ˙ ( t n ) − f ˙ ( t ) ∣ ≤ ε 2 \left|\dot{f}\left(t_{n}\right)-\dot{f}(t)\right| \leq \frac{\varepsilon}{2} ∣∣∣f˙(tn)−f˙(t)∣∣∣≤2ε
因此,对于所有 t ∈ [ t n , t n + δ ] t\in[t_n,t_n+\delta] t∈[tn,tn+δ],和所有 n ∈ N n\in\mathbb{N} n∈N,有 ∣ f ˙ ( t ) ∣ = ∣ f ˙ ( t n ) − ( f ˙ ( t n ) − f ˙ ( t ) ) ∣ ⩾ ∣ f ˙ ( t n ) ∣ − ∣ f ˙ ( t n ) − f ˙ ( t ) ∣ ⩾ ε − ε 2 = ε 2 \begin{aligned} |\dot{f}(t)| =\left|\dot{f}\left(t_{n}\right)-\left(\dot{f}\left(t_{n}\right)-\dot{f}(t)\right)\right| \geqslant \left|\dot{f}\left(t_{n}\right)\right|-\left|\dot{f}\left(t_{n}\right)-\dot{f}(t)\right| \geqslant \varepsilon-\frac{\varepsilon}{2}=\frac{\varepsilon}{2} \end{aligned} ∣f˙(t)∣=∣∣∣f˙(tn)−(f˙(tn)−f˙(t))∣∣∣⩾∣∣∣f˙(tn)∣∣∣−∣∣∣f˙(tn)−f˙(t)∣∣∣⩾ε−2ε=2ε因此,对于所有 n ∈ N n\in\mathbb{N} n∈N,有 ∣ ∫ 0 t n + δ f ˙ ( t ) d t − ∫ 0 t n f ˙ ( t ) d t ∣ = ∣ ∫ t n t n + δ f ˙ ( t ) d t ∣ = ∫ t n t n + δ ∣ f ˙ ( t ) ∣ d t ≥ ε δ 2 > 0 \left|\int_{0}^{t_{n}+\delta} \dot{f}(t) d t-\int_{0}^{t_{n}} \dot{f}(t) d t\right|=\left|\int_{t_{n}}^{t_{n}+\delta} \dot{f}(t) d t\right|=\int_{t_{n}}^{t_{n}+\delta}|\dot{f}(t)| d t \geq \frac{\varepsilon \delta}{2}>0 ∣∣∣∣∣∫0tn+δf˙(t)dt−∫0tnf˙(t)dt∣∣∣∣∣=∣∣∣∣∣∫tntn+δf˙(t)dt∣∣∣∣∣=∫tntn+δ∣f˙(t)∣dt≥2εδ>0
根据假设可知, ∫ 0 ∞ f ˙ ( t ) d t < β \int_0^\infty \dot f(t) dt<\beta ∫0∞f˙(t)dt<β 存在,因此,当 n → ∞ n\rightarrow \infty n→∞, ∣ ∫ 0 t n + δ f ˙ ( t ) d t − ∫ 0 t n f ˙ ( t ) d t ∣ → 0 \left|\int_{0}^{t_{n}+\delta} \dot{f}(t) d t-\int_{0}^{t_{n}} \dot{f}(t) d t\right| \rightarrow 0 ∣∣∣∣∣∫0tn+δf˙(t)dt−∫0tnf˙(t)dt∣∣∣∣∣→0,和上式产生矛盾,因此反证法可证,当 t → ∞ t \rightarrow \infty t→∞ 时, f ˙ ( t ) → 0 \dot{f}(t) \rightarrow 0 f˙(t)→0。
边栏推荐
- 如何通过antd的upload控件,将图片以文件流的形式发送给服务器
- Comparison between sentinel and hystrix
- DM8 uses different databases to archive and recover after multiple failures
- Comprendre la méthode de détection des valeurs aberrantes des données
- 埃氏筛+欧拉筛+区间筛
- AcWing 244. Enigmatic cow (tree array + binary search)
- ArcGIS application (XXII) ArcMap loading lidar Las format data
- 【无标题】转发最小二乘法
- awk从入门到入土(15)awk执行外部命令
- Developers really review CSDN question and answer function, and there are many improvements~
猜你喜欢
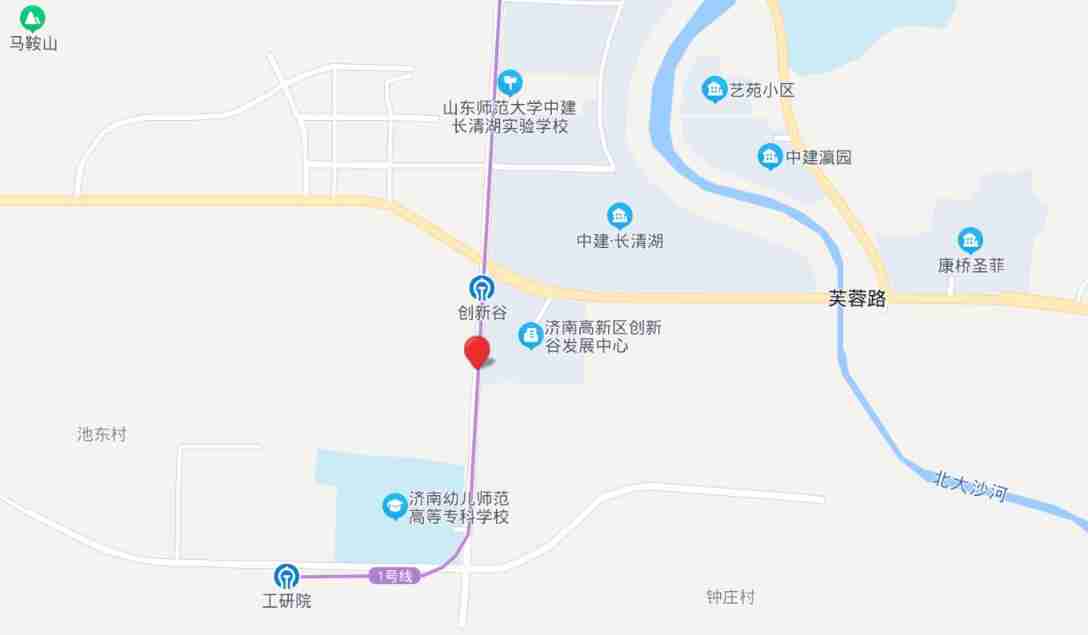
Call Baidu map to display the current position
地平线 旭日X3 PI (一)首次开机细节
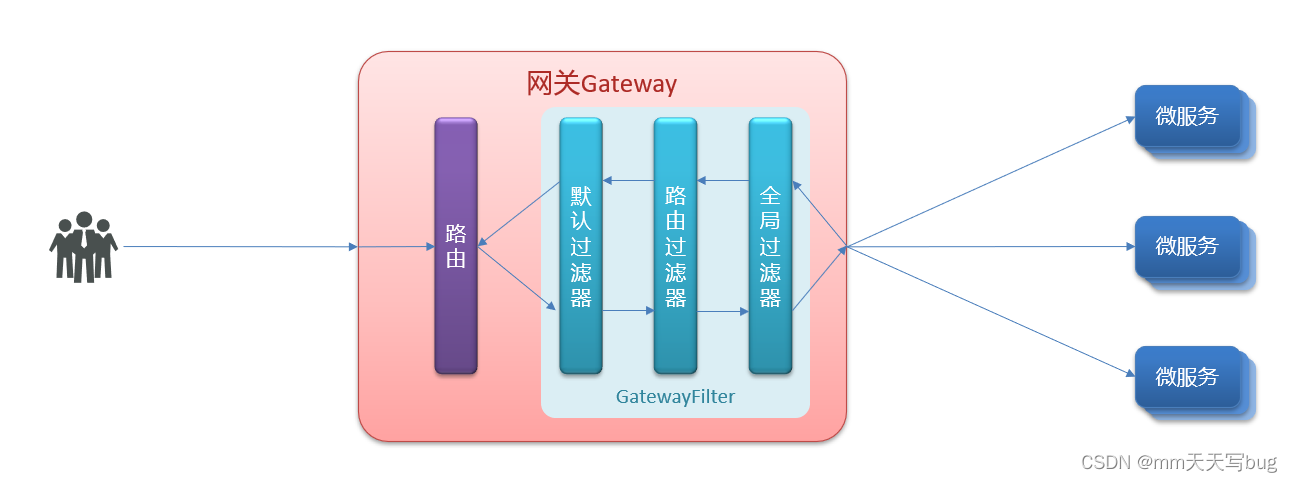
Démarrage des microservices: passerelle
Fault analysis | MySQL: unique key constraint failure
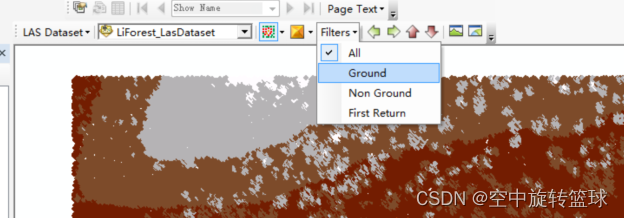
ArcGIS application (XXII) ArcMap loading lidar Las format data

Horizon sunrise X3 PI (I) first boot details
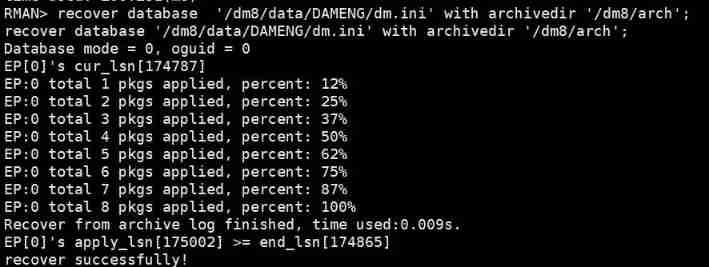
DM8 uses different databases to archive and recover after multiple failures
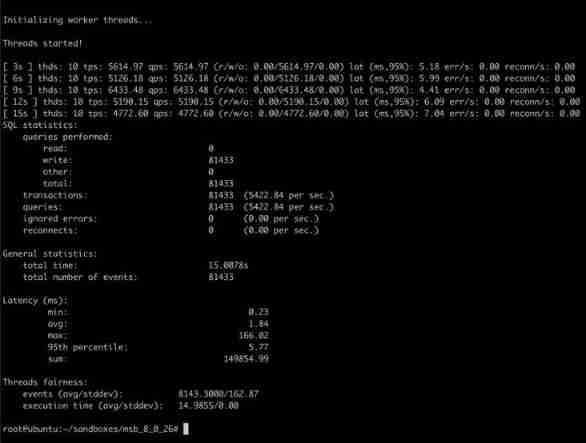
Question 49: how to quickly determine the impact of IO latency on MySQL performance
Mouse over to change the transparency of web page image
Four essential material websites for we media people to help you easily create popular models
随机推荐
deno debugger
go-zero微服务实战系列(九、极致优化秒杀性能)
小程序容器技术与物联网 IoT 可以碰撞出什么样的火花
Famous blackmail software stops operation and releases decryption keys. Most hospital IOT devices have security vulnerabilities | global network security hotspot on February 14
Snipaste convenient screenshot software, which can be copied on the screen
swatch
力扣今日题-1200. 最小绝对差
ctfshow web255 web 256 web257
Learn nuxt js
Leetcode topic [array] - 121 - the best time to buy and sell stocks
Openfeign service interface call
地平线 旭日X3 PI (一)首次开机细节
Three paradigms of database design
How to choose solid state hard disk and mechanical hard disk in computer
Go zero micro service practical series (IX. ultimate optimization of seckill performance)
Industry depression has the advantages of industry depression
Flutter 集成 amap_flutter_location
Awk from getting started to digging in (4) user defined variables
awk从入门到入土(5)简单条件匹配
Redis 哨兵机制