当前位置:网站首页>快速排序
快速排序
2022-08-02 14:11:00 【海无垠】
public void quickSort(int[] arr, int begin, int end) { //如果区间不只一个数 if (begin < end) { int temp = arr[begin]; //将区间的第一个数作为基准数 int i = begin; //从左到右进行查找时的“指针”,指示当前左位置 int j = end; //从右到左进行查找时的“指针”,指示当前右位置 //不重复遍历 while (i < j) { //当右边的数大于基准数时,略过,继续向左查找 // 不满足条件时跳出循环,此时的j对应的元素是小于基准元素的 while (i < j && arr[j] > temp) j--; if (i < j)//将右边小于等于基准元素的数填入右边相应位置 arr[i] = arr[j]; //当左边的数小于等于基准数时,略过,继续向右查找 //(重复的基准元素集合到左区间) //不满足条件时跳出循环,此时的i对应的元素是大于等于基准元素的 while (i < j && arr[i] <= temp) i++; //将左边大于基准元素的数填入左边相应位置 if (i < j) arr[j] = arr[i]; } //将基准元素填入相应位置 arr[i] = temp; //此时的i即为基准元素的位置 //对基准元素的左边子区间进行相似的快速排序 quickSort(arr, begin, i - 1); //对基准元素的右边子区间进行相似的快速排序 quickSort(arr, i + 1, end); } //如果区间只有一个数,则返回 else return; }
时间复杂度
快速排序涉及到递归调用,所以该算法的时间复杂度还需要从递归算法的复杂度开始说起;
递归算法的时间复杂度公式:T[n] = aT[n/b] + f(n) ;对于递归算法的时间复杂度这里就不展开来说了;
最优情况下时间复杂度
快速排序最优的情况就是每一次取到的元素都刚好平分整个数组(很显然我上面的不是);
此时的时间复杂度公式则为:T[n] = 2T[n/2] + f(n);T[n/2]为平分后的子数组的时间复杂度,f[n] 为平分这个数组时所花的时间;
下面来推算下,在最优的情况下快速排序时间复杂度的计算(用迭代法):
T[n] = 2T[n/2] + n ----------------第一次递归
令:n = n/2 = 2 { 2 T[n/4] + (n/2) } + n ----------------第二次递归
= 2^2 T[ n/ (2^2) ] + 2n
令:n = n/(2^2) = 2^2 { 2 T[n/ (2^3) ] + n/(2^2)} + 2n ----------------第三次递归
= 2^3 T[ n/ (2^3) ] + 3n
......................................................................................
令:n = n/( 2^(m-1) ) = 2^m T[1] + mn ----------------第m次递归(m次后结束)
当最后平分的不能再平分时,也就是说把公式一直往下跌倒,到最后得到T[1]时,说明这个公式已经迭代完了(T[1]是常量了)。
得到:T[n/ (2^m) ] = T[1] ===>> n = 2^m ====>> m = logn;
T[n] = 2^m T[1] + mn ;其中m = logn;
T[n] = 2^(logn) T[1] + nlogn = n T[1] + nlogn = n + nlogn ;其中n为元素个数
又因为当n >= 2时:nlogn >= n (也就是logn > 1),所以取后面的 nlogn;
综上所述:快速排序最优的情况下时间复杂度为:O( nlogn )
最差情况下时间复杂度
最差的情况就是每一次取到的元素就是数组中最小/最大的,这种情况其实就是冒泡排序了(每一次都排好一个元素的顺序)
这种情况时间复杂度就好计算了,就是冒泡排序的时间复杂度:T[n] = n * (n-1) = n^2 + n;
综上所述:快速排序最差的情况下时间复杂度为:O( n^2 )
平均时间复杂度
快速排序的平均时间复杂度也是:O(nlogn)
空间复杂度
其实这个空间复杂度不太好计算,因为有的人使用的是非就地排序,那样就不好计算了(因为有的人用到了辅助数组,所以这就要计算到你的元素个数了);我就分析下就地快速排序的空间复杂度吧;
首先就地快速排序使用的空间是O(1)的,也就是个常数级;而真正消耗空间的就是递归调用了,因为每次递归就要保持一些数据;
最优的情况下空间复杂度为:O(logn) ;每一次都平分数组的情况
最差的情况下空间复杂度为:O( n ) ;退化为冒泡排序的情况
边栏推荐
猜你喜欢
随机推荐
二叉排序树与 set、map
Win11系统找不到dll文件怎么修复
动态规划理论篇
casbin模型
为vscode配置clangd
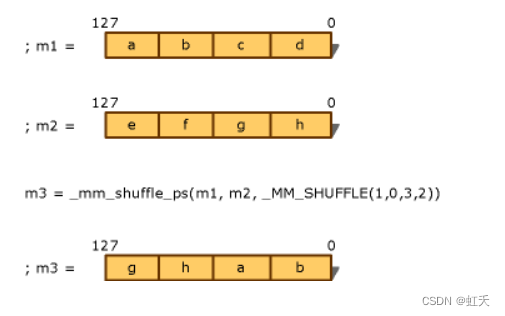
将SSE指令转换为ARM NEON指令
【系统设计与实现】基于flink的分心驾驶预测与数据分析系统
pygame图像连续旋转
Open the door of power and electricity "Circuit" (2): Power Calculation and Judgment
软件测试基础知识(背)
第二十五章:一文掌握while循环
第三十章:普通树的存储和遍历
总结计算机网络超全面试题
Win10安装了固态硬盘还是有明显卡顿怎么办?
Win11 system cannot find dll file how to fix
Win7 encounters an error and cannot boot into the desktop normally, how to solve it?
2021-10-14
SQL的通用语法和使用说明(图文)
6. Unified logging
Doubled and sparse tables