当前位置:网站首页>【九阳神功】2018复旦大学应用统计真题+解析
【九阳神功】2018复旦大学应用统计真题+解析
2022-07-06 09:20:00 【大师兄统计】
真题部分
一、(20分) 从1-10中不放回选3个数字, 求以下概率
(1)(5分) 最小数字是5;
(2)(5分) 最大数字是5;
(3)(5分) 至少一个小于6;
(4)(5分) 一个小于5, 一个等于5, 一个大于5.
二、(15分) 你在重复尝试一个成功概率为 p p p的事件, 直至连续出现两次成功或两次失败才停止, 求你以两次成功停止的概率.
三、(15分) 求二项分布, ( a , b ) (a,b) (a,b)上均匀分布, 伽马分布的期望和方差.
四、(20分) 证明 E ( X 2 ) < ∞ E\left(X^{2}\right)<\infty E(X2)<∞的充要条件是级数 ∑ n P ( ∣ X ∣ > n ) \sum n P(|X|>n) ∑nP(∣X∣>n)收敛.
五、(20分) X 1 , X 2 , X 3 X_{1}, X_{2}, X_{3} X1,X2,X3是取自期望为 α \alpha α的指数分布的随机样本, 求概率 P ( X 1 < X 2 < X 3 ) P\left(X_{1}<X_{2}<X_{3}\right) P(X1<X2<X3) 以及 X ( 1 ) X_{(1)} X(1) 的概率密度.
六、(20分) P ( X i = − 0.3 ) = P ( X i = 0.4 ) = 1 2 , i = 1 , 2 , … , n , P\left(X_{i}=-0.3\right)=P\left(X_{i}=0.4\right)=\frac{1}{2}, i=1,2, \ldots, n, P(Xi=−0.3)=P(Xi=0.4)=21,i=1,2,…,n, 相互独立, 构造随机变量序列 Y n = ∏ i = 1 n ( X i + 1 ) , Y_{n}=\prod_{i=1}^{n}\left(X_{i}+1\right), Yn=∏i=1n(Xi+1), 求 Y n Y_{n} Yn的极限并证明 Y n Y_{n} Yn的期望趋于无穷.
七、(20分) 有一堆球: 2红, 3黑, 4白. 从中随机摸一个球, 如果是黑色则记你赢, 如果是其他颜色, 则有放回的继续摸球, 直至重复出现该颜色或黑色为止, 如果出现你第一次摸到的颜色, 则你赢, 否则你输. 求你赢的概率.
八、(20分)
(1)(10分) 解释相合估计;
(2)(10分) X 1 , … , X n X_{1}, \ldots, X_{n} X1,…,Xn是来自一个同一个总体的样本, 写出一个中位数的相合估计, 并说明理由.
解析部分
一、(20分) 从1-10中不放回选3个数字, 求以下概率
(1)(5分) 最小数字是5;
(2)(5分) 最大数字是5;
(3)(5分) 至少一个小于6;
(4)(5分) 一个小于5, 一个等于5, 一个大于5.
Solution:
(1) # Ω = C 10 3 = 120 \# \Omega=C_{10}^{3}=120 #Ω=C103=120, #A A 1 = 1 ⋅ C 5 2 = 10 , P ( A 1 ) = # A 1 # Ω = 1 12 A_{1}=1 \cdot C_{5}^{2}=10, P\left(A_{1}\right)=\frac{\# A_{1}}{\# \Omega}=\frac{1}{12} A1=1⋅C52=10,P(A1)=#Ω#A1=121.
(2) # A 2 = 1 ⋅ C 4 2 = 6 , P ( A 2 ) = # A 2 # Ω = 1 20 \# A_{2}=1 \cdot C_{4}^{2}=6, P\left(A_{2}\right)=\frac{\# A_{2}}{\# \Omega}=\frac{1}{20} #A2=1⋅C42=6,P(A2)=#Ω#A2=201.
(3) # A 3 ‾ = C 5 3 = 10 , P ( A 3 ) = 1 − # A 3 ‾ # Ω = 11 12 \# \overline{A_{3}}=C_{5}^{3}=10, P\left(A_{3}\right)=1-\frac{\# \overline{A_{3}}}{\# \Omega}=\frac{11}{12} #A3=C53=10,P(A3)=1−#Ω#A3=1211.
(4) # A 4 = 4 ⋅ 1 ⋅ 5 = 20 , P ( A 4 ) = # A 4 # Ω = 1 6 \# A_{4}=4 \cdot 1 \cdot 5=20, P\left(A_{4}\right)=\frac{\# A_{4}}{\# \Omega}=\frac{1}{6} #A4=4⋅1⋅5=20,P(A4)=#Ω#A4=61.
二、(15分) 你在重复尝试一个成功概率为 p p p 的事件, 直至连续出现两次成功或两次失败才停止, 求你 以两次成功停止的概率.
Solution:
设 A A A “以两次成功停止”", p 0 = P ( A ) , p 1 = P ( A ∣ p_{0}=P(A), p_{1}=P(A \mid p0=P(A),p1=P(A∣ 第一次成功 ) , p − 1 = P ), p_{-1}=P ),p−1=P ( A ∣ A \mid A∣ 第一次失败 ) ) ), 根据全概率公式: { p 0 = p 1 ⋅ p + p − 1 ⋅ ( 1 − p ) p 1 = p + p − 1 ⋅ ( 1 − p ) p − 1 = p 1 ⋅ p \left\{\begin{array}{l} p_{0}=p_{1} \cdot p+p_{-1} \cdot(1-p) \\ p_{1}=p+p_{-1} \cdot(1-p) \\ p_{-1}=p_{1} \cdot p \end{array}\right. ⎩⎨⎧p0=p1⋅p+p−1⋅(1−p)p1=p+p−1⋅(1−p)p−1=p1⋅p 解得 p 0 = p 2 ( 2 − p ) 1 − p ( 1 − p ) p_{0}=\frac{p^{2}(2-p)}{1-p(1-p)} p0=1−p(1−p)p2(2−p).
三、(15分) 求二项分布, ( a , b ) (a,b) (a,b)上均匀分布, 伽马分布的期望和方差.
Solution:
(1) 二项分布: X ∼ B ( n , p ) , P ( X = k ) = C n k p k ( 1 − p ) n − k , k = 0 , 1 , … , n X \sim B(n, p), P(X=k)=C_{n}^{k} p^{k}(1-p)^{n-k}, k=0,1, \ldots, n X∼B(n,p),P(X=k)=Cnkpk(1−p)n−k,k=0,1,…,n,
E X = ∑ k = 0 n k n ! k ! ( n − k ) ! p k ( 1 − p ) n − k = n p ∑ k = 1 n ( n − 1 ) ! ( k − 1 ) ! ( n − k ) ! p k − 1 ( 1 − p ) n − k = n p , E X=\sum_{k=0}^{n} k \frac{n !}{k !(n-k) !} p^{k}(1-p)^{n-k}=n p \sum_{k=1}^{n} \frac{(n-1) !}{(k-1) !(n-k) !} p^{k-1}(1-p)^{n-k}=n p, EX=k=0∑nkk!(n−k)!n!pk(1−p)n−k=npk=1∑n(k−1)!(n−k)!(n−1)!pk−1(1−p)n−k=np,
E X ( X − 1 ) = ∑ k = 0 n k ( k − 1 ) C n k p k ( 1 − p ) n − k = n ( n − 1 ) p 2 ∑ k = 2 n C n − 2 k − 2 p k − 2 ( 1 − p ) n − k = n ( n − 1 ) p 2 , E X(X-1)=\sum_{k=0}^{n} k(k-1) C_{n}^{k} p^{k}(1-p)^{n-k}=n(n-1) p^{2} \sum_{k=2}^{n} C_{n-2}^{k-2} p^{k-2}(1-p)^{n-k}=n(n-1) p^{2}, EX(X−1)=k=0∑nk(k−1)Cnkpk(1−p)n−k=n(n−1)p2k=2∑nCn−2k−2pk−2(1−p)n−k=n(n−1)p2,
因此 E X 2 = n ( n − 1 ) p 2 + n p , D X = E X 2 − ( E X ) 2 = n ( n − 1 ) p 2 + n p − n 2 p 2 = n p ( 1 − p ) E X^{2}=n(n-1) p^{2}+n p, D X=E X^{2}-(E X)^{2}=n(n-1) p^{2}+n p-n^{2} p^{2}=n p(1-p) EX2=n(n−1)p2+np,DX=EX2−(EX)2=n(n−1)p2+np−n2p2=np(1−p).(2)均匀分布: X ∼ U ( a , b ) , f ( x ) = 1 b − a , a < x < b X \sim U(a, b), f(x)=\frac{1}{b-a}, a<x<b X∼U(a,b),f(x)=b−a1,a<x<b,
E X = ∫ a b x b − a d x = a + b 2 , D X = ∫ a b ( x − a + b 2 ) 2 1 b − a d x = ( b − a ) 2 12 . E X=\int_{a}^{b} \frac{x}{b-a} d x=\frac{a+b}{2}, D X=\int_{a}^{b}\left(x-\frac{a+b}{2}\right)^{2} \frac{1}{b-a} d x=\frac{(b-a)^{2}}{12} . EX=∫abb−axdx=2a+b,DX=∫ab(x−2a+b)2b−a1dx=12(b−a)2.
(3)伽马分布: X ∼ G a ( α , λ ) , f ( x ) = λ α Γ ( α ) x α − 1 e − λ x , x > 0 X \sim G a(\alpha, \lambda), f(x)=\frac{\lambda^{\alpha}}{\Gamma(\alpha)} x^{\alpha-1} e^{-\lambda x}, x>0 X∼Ga(α,λ),f(x)=Γ(α)λαxα−1e−λx,x>0,
E X = ∫ 0 + ∞ λ α Γ ( α ) x α e − λ x d x = 1 λ Γ ( α ) ∫ 0 + ∞ ( λ x ) α e − λ x d ( λ x ) = Γ ( α + 1 ) λ Γ ( α ) = α λ , E X=\int_{0}^{+\infty} \frac{\lambda^{\alpha}}{\Gamma(\alpha)} x^{\alpha} e^{-\lambda x} d x=\frac{1}{\lambda \Gamma(\alpha)} \int_{0}^{+\infty}(\lambda x)^{\alpha} e^{-\lambda x} d(\lambda x)=\frac{\Gamma(\alpha+1)}{\lambda \Gamma(\alpha)}=\frac{\alpha}{\lambda}, EX=∫0+∞Γ(α)λαxαe−λxdx=λΓ(α)1∫0+∞(λx)αe−λxd(λx)=λΓ(α)Γ(α+1)=λα,
E X 2 = ∫ 0 + ∞ λ α Γ ( α ) x α + 1 e − λ x d x = 1 λ 2 Γ ( α ) ∫ 0 + ∞ ( λ x ) α + 1 e − λ x d ( λ x ) = Γ ( α + 2 ) λ 2 Γ ( α ) = α ( α + 1 ) λ E X^{2}=\int_{0}^{+\infty} \frac{\lambda^{\alpha}}{\Gamma(\alpha)} x^{\alpha+1} e^{-\lambda x} d x=\frac{1}{\lambda^{2} \Gamma(\alpha)} \int_{0}^{+\infty}(\lambda x)^{\alpha+1} e^{-\lambda x} d(\lambda x)=\frac{\Gamma(\alpha+2)}{\lambda^{2} \Gamma(\alpha)}=\frac{\alpha(\alpha+1)}{\lambda} EX2=∫0+∞Γ(α)λαxα+1e−λxdx=λ2Γ(α)1∫0+∞(λx)α+1e−λxd(λx)=λ2Γ(α)Γ(α+2)=λα(α+1),
故 D X = E X 2 − ( E X ) 2 = α ( α + 1 ) λ 2 − α 2 λ 2 = α λ 2 . D X=E X^{2}-(E X)^{2}=\frac{\alpha(\alpha+1)}{\lambda^{2}}-\frac{\alpha^{2}}{\lambda^{2}}=\frac{\alpha}{\lambda^{2}} . DX=EX2−(EX)2=λ2α(α+1)−λ2α2=λ2α.
四、(20分) 证明 E ( X 2 ) < ∞ E\left(X^{2}\right)<\infty E(X2)<∞的充要条件是级数 ∑ n P ( ∣ X ∣ > n ) \sum n P(|X|>n) ∑nP(∣X∣>n)收敛.
Solution:
(1) 先说明 E ∣ X ∣ < + ∞ E|X|<+\infty E∣X∣<+∞ 的充要条件是级数 ∑ n = 1 ∞ P ( ∣ X ∣ > n ) \sum_{n=1}^{\infty} P(|X|>n) ∑n=1∞P(∣X∣>n) 收敛:因为 ∑ n = 1 ∞ P ( ∣ X ∣ > n ) = ∑ n = 1 ∞ ∑ k = n ∞ P ( k < ∣ X ∣ ≤ k + 1 ) = ∑ k = 1 ∞ ∑ n = 1 k P ( k < ∣ X ∣ ≤ k + 1 ) = ∑ k = 1 ∞ k P ( k < ∣ X ∣ ≤ k + 1 ) \begin{aligned} \sum_{n=1}^{\infty} P(|X|>n) &=\sum_{n=1}^{\infty} \sum_{k=n}^{\infty} P(k<|X| \leq k+1) \\ &=\sum_{k=1}^{\infty} \sum_{n=1}^{k} P(k<|X| \leq k+1) \\ &=\sum_{k=1}^{\infty} k P(k<|X| \leq k+1) \end{aligned} n=1∑∞P(∣X∣>n)=n=1∑∞k=n∑∞P(k<∣X∣≤k+1)=k=1∑∞n=1∑kP(k<∣X∣≤k+1)=k=1∑∞kP(k<∣X∣≤k+1)同时由正项级数的比较判别法, 上级数与 ∑ k = 1 ∞ ( k + 1 ) P ( k < ∣ X ∣ ≤ k + 1 ) \sum_{k=1}^{\infty}(k+1) P(k<|X| \leq k+1) ∑k=1∞(k+1)P(k<∣X∣≤k+1)也是同敛散的, 考虑到 E ∣ X ∣ = ∫ 0 + ∞ x d F ∣ X ∣ ( x ) E|X|=\int_{0}^{+\infty} x d F_{|X|}(x) E∣X∣=∫0+∞xdF∣X∣(x),一方面有 ∫ 0 + ∞ x d F ∣ X ∣ ( x ) = ∑ k = 0 ∞ ∫ k k + 1 x d F ∣ X ∣ ( x ) ≤ ∑ k = 0 ∞ ∫ k k + 1 ( k + 1 ) d F ∣ X ∣ ( x ) = ∑ k = 0 ∞ ( k + 1 ) P ( k < ∣ X ∣ ≤ k + 1 ) , \begin{aligned} \int_{0}^{+\infty} x d F_{|X|}(x) &=\sum_{k=0}^{\infty} \int_{k}^{k+1} x d F_{|X|}(x) \\ & \leq \sum_{k=0}^{\infty} \int_{k}^{k+1}(k+1) d F_{|X|}(x) \\ &=\sum_{k=0}^{\infty}(k+1) P(k<|X| \leq k+1), \end{aligned} ∫0+∞xdF∣X∣(x)=k=0∑∞∫kk+1xdF∣X∣(x)≤k=0∑∞∫kk+1(k+1)dF∣X∣(x)=k=0∑∞(k+1)P(k<∣X∣≤k+1), 另一方面有
∫ 0 + ∞ x d F ∣ X ∣ ( x ) = ∑ k = 0 ∞ ∫ k k + 1 x d F ∣ X ∣ ( x ) ≥ ∑ k = 0 ∞ ∫ k k + 1 k d F ∣ X ∣ ( x ) = ∑ k = 0 ∞ k P ( k < ∣ X ∣ ≤ k + 1 ) , \begin{aligned} \int_{0}^{+\infty} x d F_{|X|}(x) &=\sum_{k=0}^{\infty} \int_{k}^{k+1} x d F_{|X|}(x) \\ & \geq \sum_{k=0}^{\infty} \int_{k}^{k+1} k d F_{|X|}(x) \\ &=\sum_{k=0}^{\infty} k P(k<|X| \leq k+1), \end{aligned} ∫0+∞xdF∣X∣(x)=k=0∑∞∫kk+1xdF∣X∣(x)≥k=0∑∞∫kk+1kdF∣X∣(x)=k=0∑∞kP(k<∣X∣≤k+1), 综上所述, E ∣ X ∣ < + ∞ E|X|<+\infty E∣X∣<+∞ 的充要条件是级数 ∑ n = 1 ∞ P ( ∣ X ∣ > n ) \sum_{n=1}^{\infty} P(|X|>n) ∑n=1∞P(∣X∣>n) 收敛.(2) 再说明 E X 2 < + ∞ E X^{2}<+\infty EX2<+∞ 的充要条件是级数 ∑ n = 1 + ∞ n P ( ∣ X ∣ > n ) \sum_{n=1}^{+\infty} n P(|X|>n) ∑n=1+∞nP(∣X∣>n)收敛: 因为 ∑ n = 1 ∞ n P ( ∣ X ∣ > n ) = ∑ n = 1 ∞ ∑ k = n ∞ n P ( k < ∣ X ∣ ≤ k + 1 ) = ∑ k = 1 ∞ ∑ n = 1 ∞ n P ( k < ∣ X ∣ ≤ k + 1 ) = ∑ k = 1 ∞ k ( k + 1 ) 2 P ( k < ∣ X ∣ ≤ k + 1 ) \begin{aligned} \sum_{n=1}^{\infty} n P(|X|>n) &=\sum_{n=1}^{\infty} \sum_{k=n}^{\infty} n P(k<|X| \leq k+1) \\ &=\sum_{k=1}^{\infty} \sum_{n=1}^{\infty} n P(k<|X| \leq k+1) \\ &=\sum_{k=1}^{\infty} \frac{k(k+1)}{2} P(k<|X| \leq k+1) \end{aligned} n=1∑∞nP(∣X∣>n)=n=1∑∞k=n∑∞nP(k<∣X∣≤k+1)=k=1∑∞n=1∑∞nP(k<∣X∣≤k+1)=k=1∑∞2k(k+1)P(k<∣X∣≤k+1) 同时由正项级数的比较判别法, 上式的敛散性显然等同于 ∑ n = 1 ∞ n 2 P ( n < ∣ X ∣ ≤ n + 1 ) \sum_{n=1}^{\infty} n^{2} P(n<|X| \leq n+1) ∑n=1∞n2P(n<∣X∣≤n+1) 的敛散性,也等价于 ∑ n = 1 ∞ ( n + 1 ) 2 P ( n < ∣ X ∣ ≤ n + 1 ) \sum_{n=1}^{\infty}(n+1)^{2} P(n<|X| \leq n+1) ∑n=1∞(n+1)2P(n<∣X∣≤n+1) 的敛散性, 同样借助二阶矩的定 义式 E X 2 = ∫ 0 + ∞ x 2 d F ∣ X ∣ ( x ) E X^{2}=\int_{0}^{+\infty} x^{2} d F_{|X|}(x) EX2=∫0+∞x2dF∣X∣(x), 一方面有 ∫ 0 + ∞ x 2 d F ∣ X ∣ ( x ) = ∑ n = 0 ∞ ∫ n n + 1 x 2 d F ∣ X ∣ ( x ) ≤ ∑ n = 0 ∞ ∫ n n + 1 ( n + 1 ) 2 d F ∣ X ∣ ( x ) = ∑ n = 0 ∞ ( n + 1 ) 2 P ( n < ∣ X ∣ ≤ n + 1 ) \begin{aligned} \int_{0}^{+\infty} x^{2} d F_{|X|}(x) &=\sum_{n=0}^{\infty} \int_{n}^{n+1} x^{2} d F_{|X|}(x) \\ & \leq \sum_{n=0}^{\infty} \int_{n}^{n+1}(n+1)^{2} d F_{|X|}(x) \\ &=\sum_{n=0}^{\infty}(n+1)^{2} P(n<|X| \leq n+1) \end{aligned} ∫0+∞x2dF∣X∣(x)=n=0∑∞∫nn+1x2dF∣X∣(x)≤n=0∑∞∫nn+1(n+1)2dF∣X∣(x)=n=0∑∞(n+1)2P(n<∣X∣≤n+1)
另一方面有 ∫ 0 + ∞ x 2 d F ∣ X ∣ ( x ) = ∑ n = 0 ∞ ∫ n n + 1 x 2 d F ∣ X ∣ ( x ) ≤ ∑ n = 0 ∞ ∫ n n + 1 n 2 d F ∣ X ∣ ( x ) = ∑ n = 0 ∞ n 2 P ( n < ∣ X ∣ ≤ n + 1 ) , \begin{aligned} \int_{0}^{+\infty} x^{2} d F_{|X|}(x) &=\sum_{n=0}^{\infty} \int_{n}^{n+1} x^{2} d F_{|X|}(x) \\ & \leq \sum_{n=0}^{\infty} \int_{n}^{n+1} n^{2} d F_{|X|}(x) \\ &=\sum_{n=0}^{\infty} n^{2} P(n<|X| \leq n+1), \end{aligned} ∫0+∞x2dF∣X∣(x)=n=0∑∞∫nn+1x2dF∣X∣(x)≤n=0∑∞∫nn+1n2dF∣X∣(x)=n=0∑∞n2P(n<∣X∣≤n+1), 综上所述, E X 2 < + ∞ E X^{2}<+\infty EX2<+∞ 的充要条件是级数 ∑ n = 1 + ∞ n P ( ∣ X ∣ > n ) \sum_{n=1}^{+\infty} n P(|X|>n) ∑n=1+∞nP(∣X∣>n) 收敛.
五、(20分) X 1 , X 2 , X 3 X_{1}, X_{2}, X_{3} X1,X2,X3是取自期望为 α \alpha α的指数分布的随机样本, 求概率 P ( X 1 < X 2 < X 3 ) P\left(X_{1}<X_{2}<X_{3}\right) P(X1<X2<X3) 以及 X ( 1 ) X_{(1)} X(1) 的概率密度.
Solution:
根据轮换对称性, P ( X 1 < X 2 < X 3 ) = 1 6 P\left(X_{1}<X_{2}<X_{3}\right)=\frac{1}{6} P(X1<X2<X3)=61. 令 Y = X ( 1 ) Y=X_{(1)} Y=X(1), 则当 y > 0 y>0 y>0 时, 1 − F ( y ) = P { Y > y } = P 3 { X 1 > y } = e − 3 α y 1-F(y)=P\{Y>y\}=P^{3}\left\{X_{1}>y\right\}=e^{-\frac{3}{\alpha} y} 1−F(y)=P{ Y>y}=P3{ X1>y}=e−α3y, 故 f ( y ) = 3 α e − 3 α y , y > 0 f(y)=\frac{3}{\alpha} e^{-\frac{3}{\alpha} y}, y>0 f(y)=α3e−α3y,y>0. 这恰好是 Exp ( 3 α ) \operatorname{Exp}\left(\frac{3}{\alpha}\right) Exp(α3).
六、(20分) P ( X i = − 0.3 ) = P ( X i = 0.4 ) = 1 2 , i = 1 , 2 , … , n , P\left(X_{i}=-0.3\right)=P\left(X_{i}=0.4\right)=\frac{1}{2}, i=1,2, \ldots, n, P(Xi=−0.3)=P(Xi=0.4)=21,i=1,2,…,n, 相互独立, 构造随机变量序列 Y n = ∏ i = 1 n ( X i + 1 ) , Y_{n}=\prod_{i=1}^{n}\left(X_{i}+1\right), Yn=∏i=1n(Xi+1), 求 Y n Y_{n} Yn的极限并证明 Y n Y_{n} Yn的期望趋于无穷.
Solution:
由强大数律, 1 n ln Y n = 1 n ∑ i = 1 n ln ( X i + 1 ) * a.s. E ln ( X 1 + 1 ) = 1 2 ln 0.98 < 0 \frac{1}{n} \ln Y_{n}=\frac{1}{n} \sum_{i=1}^{n} \ln \left(X_{i}+1\right) \stackrel{\text { a.s. }}{\longrightarrow} E \ln \left(X_{1}+1\right)=\frac{1}{2} \ln 0.98<0 n1lnYn=n1∑i=1nln(Xi+1)* a.s. Eln(X1+1)=21ln0.98<0, 故 ln Y n * a.s. − ∞ , Y n * a.s. 0 \ln Y_{n} \stackrel{\text { a.s. }}{\longrightarrow}-\infty, Y_{n} \stackrel{\text { a.s. }}{\longrightarrow} 0 lnYn* a.s. −∞,Yn* a.s. 0, 因此 Y n Y_{n} Yn 的极限是单点分布, 以概率 1 取 0 . 而 E Y n = ∏ i = 1 n E ( X i + 1 ) = ∏ i = 1 n ( 0.7 + 1.4 2 ) = 1.0 5 n → + ∞ . E Y_{n}=\prod_{i=1}^{n} E\left(X_{i}+1\right)=\prod_{i=1}^{n}\left(\frac{0.7+1.4}{2}\right)=1.05^{n} \rightarrow+\infty. EYn=i=1∏nE(Xi+1)=i=1∏n(20.7+1.4)=1.05n→+∞.
七、(20分) 有一堆球: 2红, 3黑, 4白. 从中随机摸一个球, 如果是黑色则记你赢, 如果是其他颜色, 则有放回的继续摸球, 直至重复出现该颜色或黑色为止, 如果出现你第一次摸到的颜色, 则你赢, 否则你输. 求你赢的概率.
Solution:
设 A k A_k Ak为第 k k k次赢的概率, 待求结果为 P ( A ) = P ( ⋃ k = 1 ∞ A k ) = ∑ k = 1 ∞ P ( A k ) P(A)=P(\bigcup_{k=1}^{\infty}A_k)=\sum_{k=1}^{\infty}P(A_k) P(A)=P(⋃k=1∞Ak)=∑k=1∞P(Ak).
(i) 第一次赢的概率 P ( A 1 ) = 1 3 P(A_1)=\frac{1}{3} P(A1)=31.
(ii) 第 k k k次赢( k > 1 k>1 k>1)表明: 第一次未摸到黑球, 后续的 2 , 3 , . . . , k − 1 2,3,...,k-1 2,3,...,k−1次没有摸到黑也没有摸到你第一次摸中的颜色, 最后第 k k k次摸中了最初的颜色, 这一概率肯定与你最初摸到的颜色有关, 考虑全概率公式 P ( A k ) = P ( R ) P ( A k ∣ R ) + P ( W ) P ( A k ∣ W ) P(A_k)=P(R)P(A_k|R)+P(W)P(A_k|W) P(Ak)=P(R)P(Ak∣R)+P(W)P(Ak∣W), 其中 R R R表示摸到红, W W W表示摸到白, 有
P ( A k ∣ R ) = ( 4 9 ) k − 2 2 9 , P ( A k ∣ W ) = ( 2 9 ) k − 2 4 9 . P\left( A_k|R \right) =\left( \frac{4}{9} \right) ^{k-2}\frac{2}{9},\quad P\left( A_k\mid W \right) =\left( \frac{2}{9} \right) ^{k-2}\frac{4}{9}. P(Ak∣R)=(94)k−292,P(Ak∣W)=(92)k−294. 因此 P ( A k ) = P ( R ) 2 9 ( 4 9 ) k − 2 + P ( W ) 4 9 ( 2 9 ) k − 2 = 4 81 ( 4 9 ) k − 2 + 16 81 ( 2 9 ) k − 2 . P\left( A_k \right) =P\left( R \right) \frac{2}{9}\left( \frac{4}{9} \right) ^{k-2}+P\left( W \right) \frac{4}{9}\left( \frac{2}{9} \right) ^{k-2}=\frac{4}{81}\left( \frac{4}{9} \right) ^{k-2}+\frac{16}{81}\left( \frac{2}{9} \right) ^{k-2}. P(Ak)=P(R)92(94)k−2+P(W)94(92)k−2=814(94)k−2+8116(92)k−2. 进行求和, 有
P ( A ) = P ( A 1 ) + 4 81 ( 1 − 4 9 ) + 16 81 ( 1 − 2 9 ) = 1 3 + 4 45 + 16 63 = 71 105 . P\left( A \right) =P\left( A_1 \right) +\frac{4}{81\left( 1-\frac{4}{9} \right)}+\frac{16}{81\left( 1-\frac{2}{9} \right)}=\frac{1}{3}+\frac{4}{45}+\frac{16}{63}=\frac{71}{105}. P(A)=P(A1)+81(1−94)4+81(1−92)16=31+454+6316=10571.
八、(20分)
(1)(10分) 解释相合估计;
(2)(10分) X 1 , … , X n X_{1}, \ldots, X_{n} X1,…,Xn是来自一个同一个总体的样本, 写出一个中位数的相合估计, 并说明理由.
Solution:
(1) g ^ \hat{g} g^ 是 g g g 的相合估计意味着 g ^ → p g \hat{g} \stackrel{p}{\rightarrow} g g^→pg, 这说明了 g ^ \hat{g} g^ 是一个很好的估计, 至少在样本量 n n n 较大时, 它偏离 g g g 的概率极小. 更进一步, 如果说 g ^ \hat{g} g^ 是 g g g 的强相合估计意味着 g ^ * a.s. g \hat{g} \stackrel{\text { a.s. }}{\longrightarrow} g g^* a.s. g.(2) 样本中位数 X [ n 2 ] X_{\left[\frac{n}{2}\right]} X[2n] 就是总体中位数 x 0.5 x_{0.5} x0.5 的相合估计量, 设总体密度函数为 f ( x ) f(x) f(x), 有样本中位数的渐近正态分布 X [ n 2 ] ∼ N ( x 0.5 , 1 4 n f 2 ( x 0.5 ) ) , X_{\left[\frac{n}{2}\right]} \sim N\left(x_{0.5}, \frac{1}{4 n f^{2}\left(x_{0.5}\right)}\right), X[2n]∼N(x0.5,4nf2(x0.5)1), 由其渐近正态分布可以得到 P ( ∣ X [ n 2 ] − x 0.5 ∣ < ε ) = P ( 2 n f ( x 0.5 ) ∣ X [ n 2 ] − x 0.5 ∣ < 2 n f ( x 0.5 ) ε ) ∼ Φ ( 2 n f ( x 0.5 ) ε ) − Φ ( − 2 n f ( x 0.5 ) ε ) → 1. P\left( \left| X_{\left[ \frac{n}{2} \right]}-x_{0.5} \right|<\varepsilon \right) =P\left( 2\sqrt{n}f\left( x_{0.5} \right) \left| X_{\left[ \frac{n}{2} \right]}-x_{0.5} \right|<2\sqrt{n}f\left( x_{0.5} \right) \varepsilon \right) \sim \Phi \left( 2\sqrt{n}f\left( x_{0.5} \right) \varepsilon \right) -\Phi \left( -2\sqrt{n}f\left( x_{0.5} \right) \varepsilon \right) \rightarrow 1. P(∣∣∣X[2n]−x0.5∣∣∣<ε)=P(2nf(x0.5)∣∣∣X[2n]−x0.5∣∣∣<2nf(x0.5)ε)∼Φ(2nf(x0.5)ε)−Φ(−2nf(x0.5)ε)→1.上式说明了样本中位数 X [ n 2 ] X_{\left[\frac{n}{2}\right]} X[2n] 就是总体中位数 x 0.5 x_{0.5} x0.5 的相合估计量.
边栏推荐
- Common method signatures and meanings of Iterable, collection and list
- 系统设计学习(一)Design Pastebin.com (or Bit.ly)
- View UI Plus 发布 1.2.0 版本,新增 Image、Skeleton、Typography组件
- Wei Pai: the product is applauded, but why is the sales volume still frustrated
- Tyut Taiyuan University of technology 2022 introduction to software engineering
- View UI plus released version 1.3.1 to enhance the experience of typescript
- 165. Compare version number - string
- [中国近代史] 第六章测验
- Interview Essentials: talk about the various implementations of distributed locks!
- Atomic and nonatomic
猜你喜欢

西安电子科技大学22学年上学期《基础实验》试题及答案
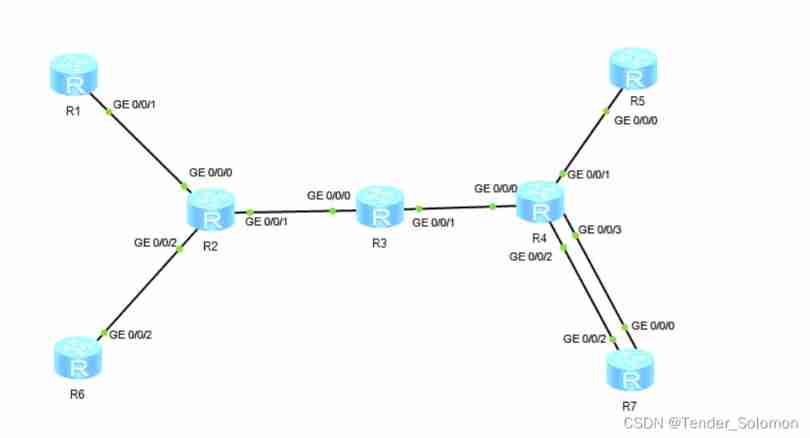
MPLS experiment
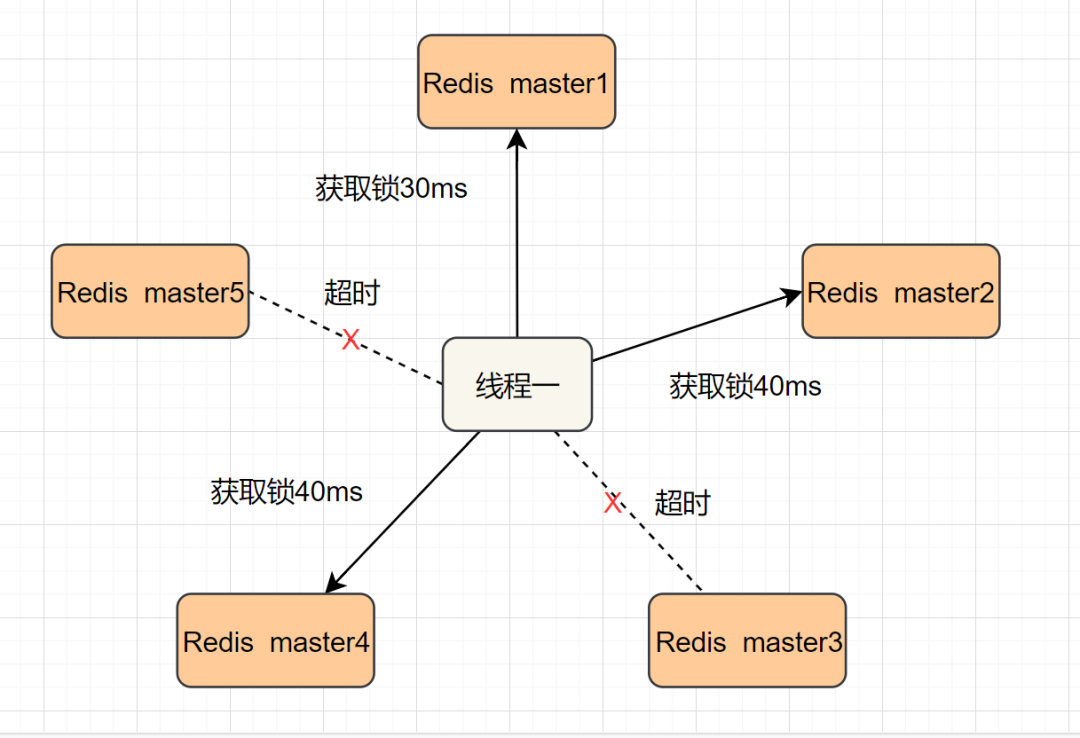
Interview Essentials: talk about the various implementations of distributed locks!

C语言实现扫雷游戏(完整版)
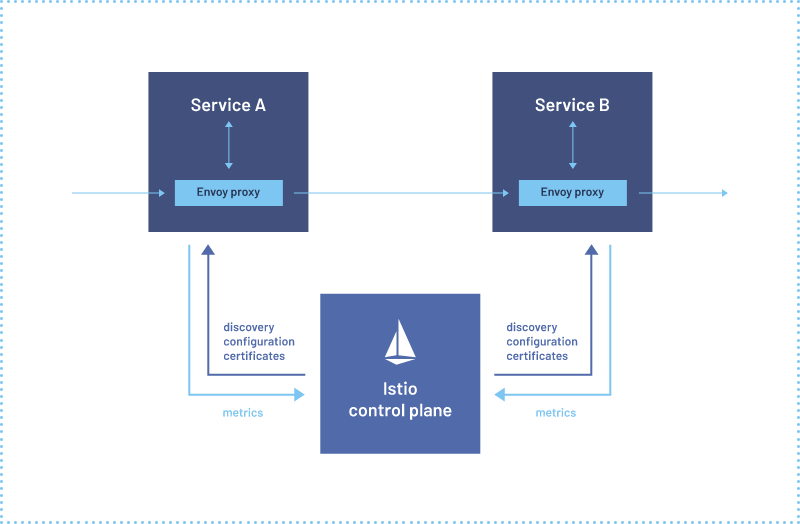
阿里云微服务(四) Service Mesh综述以及实例Istio

西安电子科技大学22学年上学期《射频电路基础》试题及答案
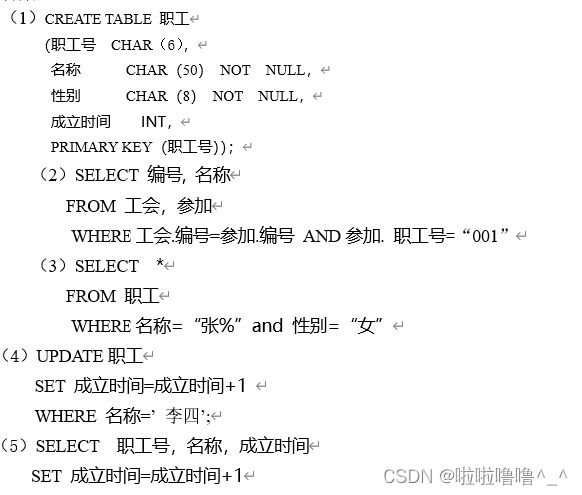
Database operation of tyut Taiyuan University of technology 2022 database

5.MSDN的下载和使用
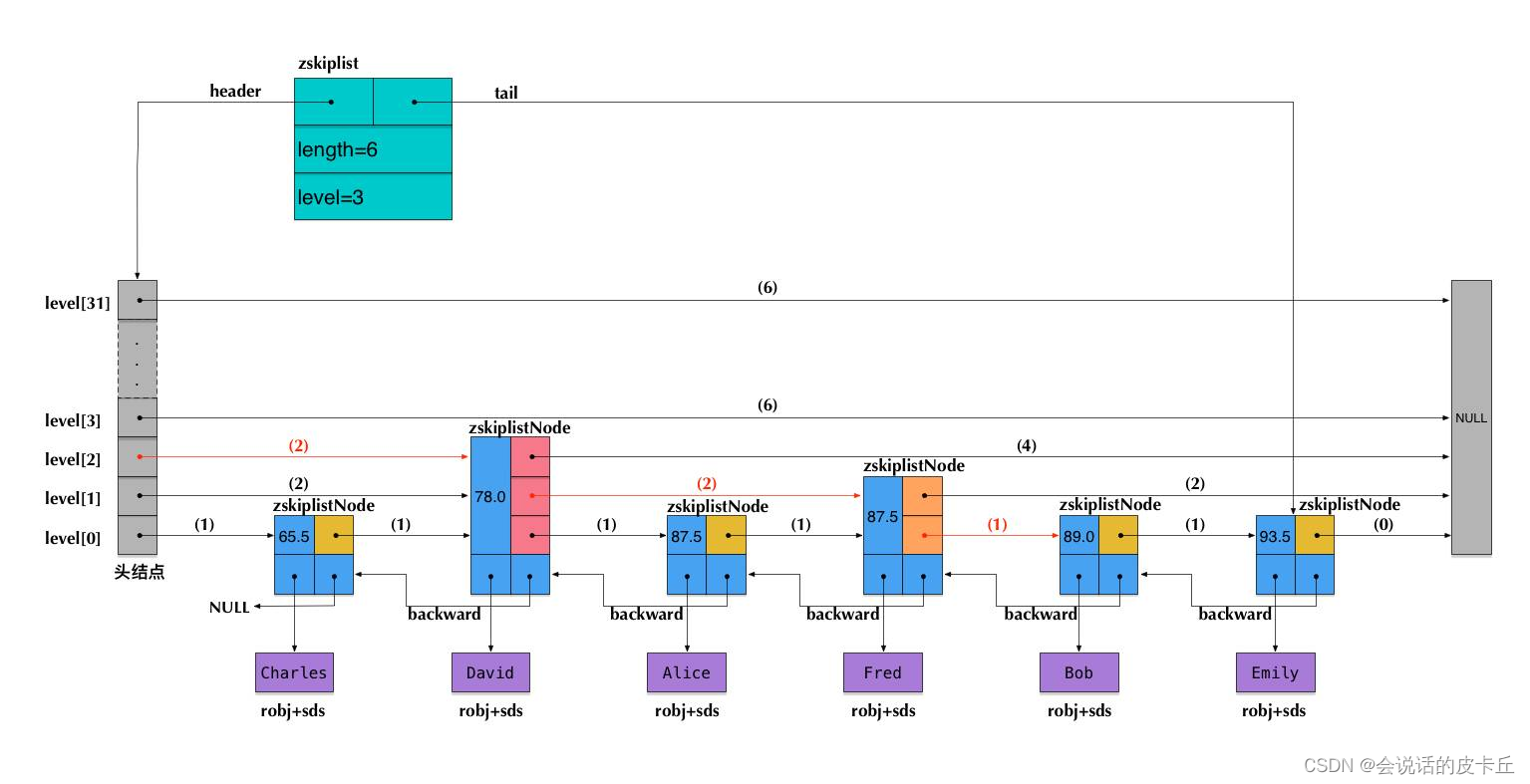
Introduction and use of redis

TYUT太原理工大学2022“mao gai”必背
随机推荐
165. Compare version number - string
TYUT太原理工大学2022数据库大题之E-R图转关系模式
Alibaba cloud side: underlying details in concurrent scenarios - pseudo sharing
系统设计学习(一)Design Pastebin.com (or Bit.ly)
167. Sum of two numbers II - input ordered array - Double pointers
系统设计学习(二)Design a key-value cache to save the results of the most recent web server queries
MySQL 30000 word essence summary + 100 interview questions, hanging the interviewer is more than enough (Collection Series
Questions and answers of "Fundamentals of RF circuits" in the first semester of the 22nd academic year of Xi'an University of Electronic Science and technology
Tyut outline of 2022 database examination of Taiyuan University of Technology
3.猜数字游戏
Alibaba cloud microservices (III) sentinel open source flow control fuse degradation component
Floating point comparison, CMP, tabulation ideas
3. Number guessing game
1.C语言矩阵加减法
西安电子科技大学22学年上学期《基础实验》试题及答案
Wei Pai: the product is applauded, but why is the sales volume still frustrated
Tyut Taiyuan University of technology 2022 introduction to software engineering
Record: newinstance() obsolete replacement method
Pit avoidance Guide: Thirteen characteristics of garbage NFT project
List set map queue deque stack