当前位置:网站首页>LeetCode 1031. Maximum sum of two non overlapping subarrays
LeetCode 1031. Maximum sum of two non overlapping subarrays
2022-07-07 16:58:00 【@Little safflower】
Problem description
Give an array of nonnegative integers A , Return two non overlapping ( continuity ) The maximum sum of elements in a subarray , The length of the subarray is L and M.( What needs to be clarified here is , Long for L The subarray of can appear at length as M Before or after the subarray of .)
In form , Return to the biggest V, and V = (A[i] + A[i+1] + ... + A[i+L-1]) + (A[j] + A[j+1] + ... + A[j+M-1]) And meet one of the following conditions :
0 <= i < i + L - 1 < j < j + M - 1 < A.length, or
0 <= j < j + M - 1 < i < i + L - 1 < A.length.
Example 1:
Input :A = [0,6,5,2,2,5,1,9,4], L = 1, M = 2
Output :20
explain : In a selection of subarrays ,[9] The length is 1,[6,5] The length is 2.
Example 2:Input :A = [3,8,1,3,2,1,8,9,0], L = 3, M = 2
Output :29
explain : In a selection of subarrays ,[3,8,1] The length is 3,[8,9] The length is 2.
Example 3:Input :A = [2,1,5,6,0,9,5,0,3,8], L = 4, M = 3
Output :31
explain : In a selection of subarrays ,[5,6,0,9] The length is 4,[0,3,8] The length is 3.
Tips :
L >= 1
M >= 1
L + M <= A.length <= 1000
0 <= A[i] <= 1000source : Power button (LeetCode)
link :https://leetcode.cn/problems/maximum-sum-of-two-non-overlapping-subarrays
Copyright belongs to the network . For commercial reprint, please contact the official authority , Non-commercial reprint please indicate the source .
java
class Solution {
public int maxSumTwoNoOverlap(int[] nums, int firstLen, int secondLen) {
int n = nums.length;
// The prefix and
int[] sum = new int[n + 1];
for(int i = 0;i < n;i++){
sum[i + 1] = sum[i] + nums[i];
}
// In exchange for
if(firstLen > secondLen){
firstLen ^= secondLen;
secondLen ^= firstLen;
firstLen ^= secondLen;
}
int[][] dp = new int[n + 1][2];
int ans = 0;
// From firstLen Start
for(int i = firstLen;i <= n;i++){
// The current element has been closed before firstLen And
int s1 = sum[i] - sum[i - firstLen];
dp[i][0] = Math.max(dp[i - 1][0],s1);
ans = Math.max(ans,s1 + dp[i - firstLen][1]);
if(i >= secondLen){
int s2 = sum[i] - sum[i - secondLen];
dp[i][1] = Math.max(dp[i - 1][1],s2);
ans = Math.max(ans,s2 + dp[i - secondLen][0]);
}
}
return ans;
}
}
边栏推荐
- Laravel5.1 Routing - routing packets
- LeetCode 120. 三角形最小路径和 每日一题
- Master this promotion path and share interview materials
- 【DesignMode】外观模式 (facade patterns)
- Imitate the choice of enterprise wechat conference room
- [C language] question set of X
- 【Seaborn】组合图表:PairPlot和JointPlot
- The latest interview experience of Android manufacturers in 2022, Android view+handler+binder
- 如何选择合适的自动化测试工具?
- 数据中台落地实施之法
猜你喜欢
QT中自定义控件的创建到封装到工具栏过程(一):自定义控件的创建
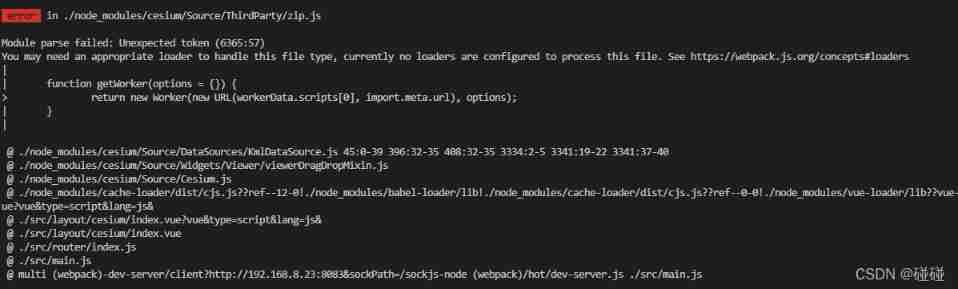
Cesium(3):ThirdParty/zip. js

1亿单身男女“在线相亲”,撑起130亿IPO
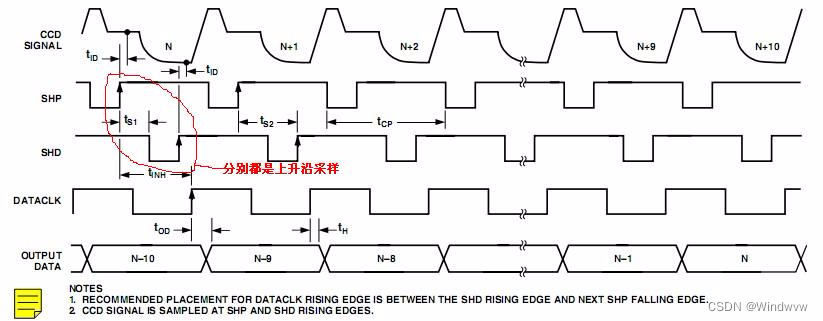
【图像传感器】相关双采样CDS
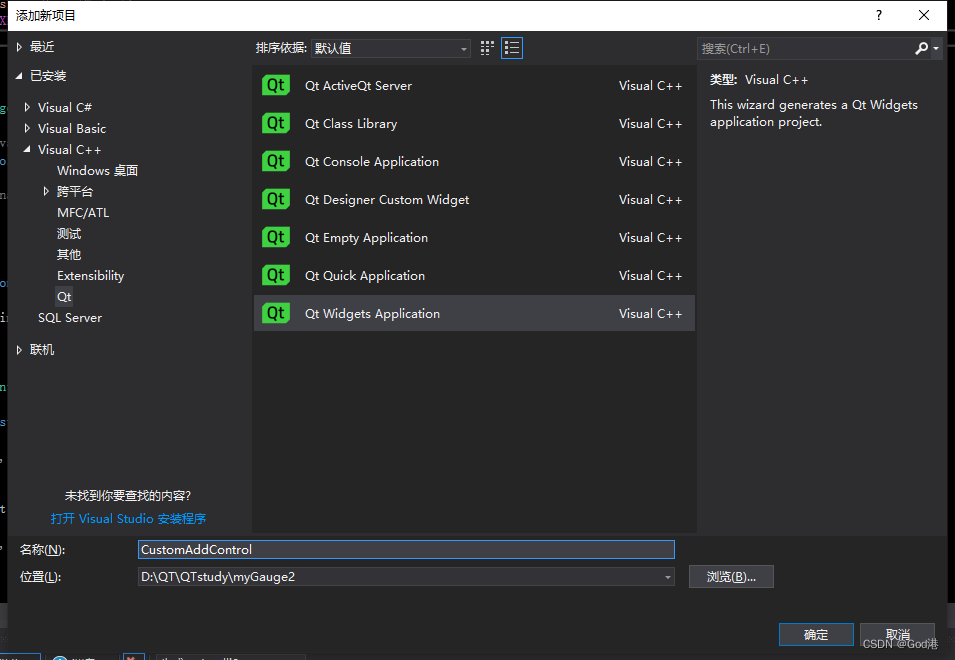
QT中自定义控件的创建到封装到工具栏过程(二):自定义控件封装到工具栏
整理几个重要的Android知识,高级Android开发面试题
![[C language] question set of X](/img/17/bfa57de183c44cf0a3c6637bb65a9d.jpg)
[C language] question set of X
The latest interview experience of Android manufacturers in 2022, Android view+handler+binder
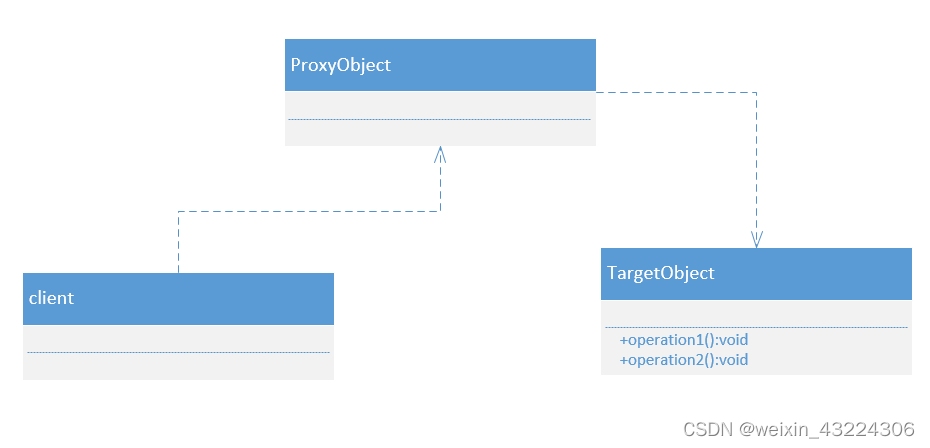
【DesignMode】代理模式(proxy pattern)
ByteDance Android gold, silver and four analysis, Android interview question app
随机推荐
QML初学
1亿单身男女“在线相亲”,撑起130亿IPO
【图像传感器】相关双采样CDS
Personal notes of graphics (4)
LeetCode 1477. 找两个和为目标值且不重叠的子数组 每日一题
Three. JS series (2): API structure diagram-2
LeetCode 403. 青蛙过河 每日一题
Temperature sensor chip used in temperature detector
Opencv personal notes
应用在温度检测仪中的温度传感芯片
Deep listening array deep listening watch
二叉搜索树(基操篇)
Binary search tree (features)
time标准库
AutoLISP series (1): function function 1
Build an all in one application development platform, light flow, and establish a code free industry benchmark
LeetCode 1043. 分隔数组以得到最大和 每日一题
[summary of knowledge] summary of notes on using SVN in PHP
Pisa-Proxy SQL 解析之 Lex & Yacc
【DesignMode】外观模式 (facade patterns)