C code implementation of robust estimation in rtklib's pntpos function (standard single point positioning spp)

One 、 background

stay rtklib in spp The location algorithm is mainly in pntpos Function ,pvt stay pntpos The realization is incisive .
1. In terms of the types of observations ：
（1） If we have pseudo range observations , So it can be estpos To analyze the stability of positioning and receiver clock error ;（2） If we still have Doppler shift , So it can be estvel The constant speed , Of course , If we have carrier observations , The speed can also be fixed through the carrier difference between epochs .
2. In terms of the frequency of observations ：
（1） If we are double frequency pseudo range observations , Then according to our different treatment strategies for the ionosphere , The types of observations used are also different , say concretely , If we use the ionospheric combination , Then we need to use the double frequency observations to combine the pseudorange de ionosphere to get the combined observations ; If we use brdc Deal with ionospheric delays , Then we only use L1 Pseudo range observations , If we use TEQC Conduct data quality analysis , You will find L1 Than L2 Of mp1 To be less than mp2, in addition , We're doing rtk When , The calculation of the number of effective satellites is also based on L1 To accumulate .
3. Tolerance spp The necessity of ：
Why spp Robust estimation of ？ Because when we carry out high-precision positioning ,spp It's for kalman filter initial value , If the initial value is not correct , Then we pass filter Got float The solution deviates from the actual position , Will cause fix The latter solution is also wrong , For example, the phenomenon of flying points .
4. spp Introduction to mathematical model ：
In the grasp of spp Based on the mathematical model of , The mathematical model consists of a functional model and a stochastic model , The function model is the pseudo range observation equation , Stochastic models include prior stochastic models （ Equal weight model 、 Height angle random model 、 Signal noise ratio random model ） And a posteriori random model （helmet Variance component estimation ）, The function model allows us to get the error equation v=Bx-l, The random model gives us the weight matrix P. So in rtklib Of spp in , Is obtained by using weighted iterative least squares dx, And then with the initial value x0 Add to get pos and dt value .
5.spp Random models ：
About stochastic models , Want to say more , If a friend wants to use helmet Variance component estimation , Then we should ensure that the priori weight matrix is as accurate as possible , Otherwise, it's nonsense , Actually in rtklib in varerr Weight ratio in function , We can use helmet To get , for example ,gps and bds stay spp Is the middle weight the same , Even in bds in ,geo/meo/igso Is the weight of the same ？ You can practice it . in addition ,rtklib In the height angle random model sin(el) There is no square , have access to SQR(sin(el)). Speaking of this , I have a supplementary , The variance of observation error is composed of three parts , Satellite position variance （ Satellite side ）, Atmospheric delay variance （ The communication end , the ionosphere 、 The troposphere ）, The measurement error obtained by using the random model （ Receiver end , That is, where random models are used ）.

Two 、 Tolerance spp Realization

stay rtklib in , Epoch k There are many iterations , The maximum number of iterations is 10, Even in the case of first positioning , That is, the state vector （ With unknown vector 、 Unknown parameter means ） All for 0 When , It just needs 6 The final result can be obtained in one iteration , Subsequent epochs generally require 3 Times to get the final result , Yes, of course , The result may be incorrect , This is the time valpos The function works ,valpos Mainly through chi square test and dop Value test is used to test the effectiveness , If it fails , Then the result of the epoch will not be output , Some friends may not notice this , Your focus may be lsq More .

2.1. Robust estimation code
rtklib in spp The code of robust estimation applied on is as follows , I first find the largest value through the standardized residual to eliminate , I only have zero rights and guaranteed rights , Specific application data, and then modify the details . The code is as follows ：

/* compare residual data -------------------------------------------------*/
static int cmpres(const void *p1, const void *p2)
{
	double *q1 = (double *)p1, *q2 = (double *)p2;
	double delta = *q1 - *q2;
	return delta<-0.0 ? -1 : (delta>0.0 ? 1 : 0);
}

/* estimate receiver position ------------------------------------------------*/
static int estpos(const obsd_t *obs, int n, const double *rs, const double *dts,
                  const double *vare, const int *svh, const nav_t *nav,
                  const prcopt_t *opt, sol_t *sol, double *azel, int *vsat,
                  double *resp, char *msg)
{
    double x[NX]={0},dx[NX],Q[NX*NX],*v,*H,*v_,*var,sig;
    int i,j,k,info,stat,nv,ns;
	double k0=8.0;
	int ref = 0; // robust estimate start flag

    trace(3,"estpos  : n=%d\n",n);
	
    v=mat(n+4,1); H=mat(NX,n+4); var=mat(n+4,1);
	v_ = mat(n + 4, 1); // deal with residual(derive from [v])
    
    for (i=0;i<3;i++) x[i]=sol->rr[i];
    
    for (i=0;i<MAXITR;i++) {
        
        /* pseudo range residuals */
        nv=rescode(i,obs,n,rs,dts,vare,svh,nav,x,opt,v,H,var,azel,vsat,resp,
                   &ns);// H Is in accordance with the nv*NX Arranged , namely nv For the number of lines ,NX Represents the number of columns , Constant for the 7
		matcpy(v_, v, ns, 1);
		// predicted normalized residual
		qsort(v_, ns, sizeof(double), cmpres);
		if (fabs(v_[0] < 100 && fabs(v_[ns - 1]) < 100))
		{
			ref = 1;
		}

		if (ref == 1) // robust estimate start
		{
			matcpy(v_, v, ns, 1);
			for (j = 0; j < ns; j++)
			{
				v_[j] = fabs(v_[j]) / sqrt(var[j]);
			}
			qsort(v_, ns, sizeof(double), cmpres);

			// local variable
			int v_max_index=0; // the biggest normalized residual index
			double  v_max= v_[ns - 1]; // the biggest normalized residual value

			matcpy(v_, v, ns, 1);
			for (j = 0; j < ns; j++)
			{
				v_[j] = sqrt(SQR(v_[j]) / var[j]);
				if (fabs(v_[j] -v_max)<1e-9)
				{
					v_max_index = j;
					break;
				}
			}

			if (v_max > k0)
			{
				if (ns > 4)
				{
					v[v_max_index] = 0;
					for (k = 0; k < NX; k++) H[k + v_max_index*NX] = 0;
				}

			}
		}

        if (nv<NX) {
            sprintf(msg,"lack of valid sats ns=%d",nv);
            break;
        }
        /* weight by variance */
        for (j=0;j<nv;j++) {
            sig=sqrt(var[j]);
            v[j]/=sig;
            for (k=0;k<NX;k++) H[k+j*NX]/=sig;
        }

        /* least square estimation */
        if ((info=lsq(H,v,NX,nv,dx,Q))) {
            sprintf(msg,"lsq error info=%d",info);
            break;
        }
		
        for (j=0;j<NX;j++) x[j]+=dx[j];
        
        if (norm(dx,NX)<1E-4) {
            sol->type=0;
            sol->time=timeadd(obs[0].time,-x[3]/CLIGHT);
            sol->dtr[0]=x[3]/CLIGHT; /* receiver clock bias (s) */
            sol->dtr[1]=x[4]/CLIGHT; /* glo-gps time offset (s) */
            sol->dtr[2]=x[5]/CLIGHT; /* gal-gps time offset (s) */
            sol->dtr[3]=x[6]/CLIGHT; /* bds-gps time offset (s) */
            for (j=0;j<6;j++) sol->rr[j]=j<3?x[j]:0.0;
            for (j=0;j<3;j++) sol->qr[j]=(float)Q[j+j*NX];
            sol->qr[3]=(float)Q[1];    /* cov xy */
            sol->qr[4]=(float)Q[2+NX]; /* cov yz */
            sol->qr[5]=(float)Q[2];    /* cov zx */
            sol->ns=(unsigned char)ns;
            sol->age=sol->ratio=0.0;
            
            /* validate solution */
            if ((stat=valsol(azel,vsat,n,opt,v,nv,NX,msg))) {
                sol->stat=opt->sateph==EPHOPT_SBAS?SOLQ_SBAS:SOLQ_SINGLE;
            }
            free(v); free(H); free(var);
            
            return stat;
        }
    }
    if (i>=MAXITR) sprintf(msg,"iteration divergent i=%d",i);
    
    free(v); free(H); free(var);
    
    return 0;
}

2.2. The test data
Use a piece of data from the self-test , Strong signal , Static data measured in the open sky , The information in the header file is as follows ：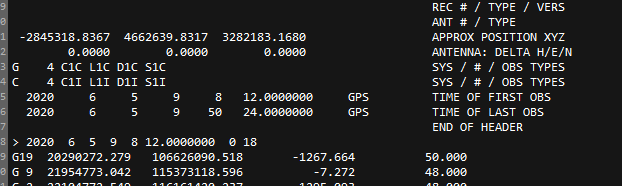

I'm in the calendar [2020 6 5 9 8 14.0000000] Yes G09 Satellite pseudo range observations are applied 100m Gross error of , by 21954773.950 Turned into 21954873.950.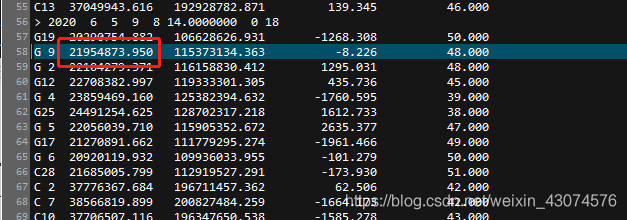

Robust estimation is not used , The result obtained directly from the iterative least squares is ：

Then if robust estimation is used, the result is ：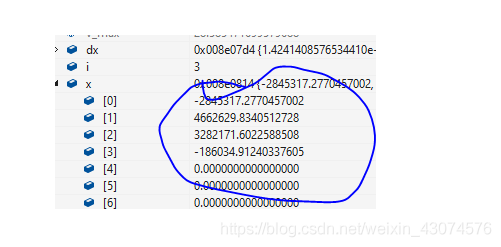

The first two epochs s There is no gross error pollution in the observed value , Its spp The results are ：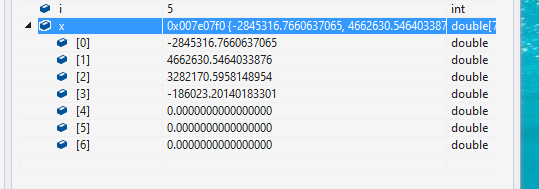


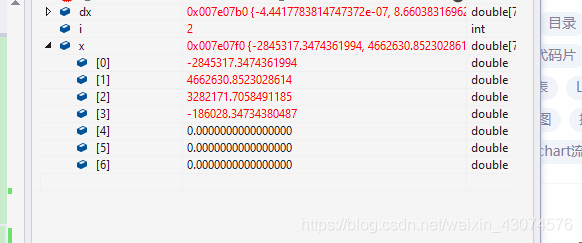
It can be seen that the resistance is poor spp It has good reliability and positioning accuracy .
// Updated on 2020.11.27 01：36：00