当前位置:网站首页>堆排序【手写小根堆】
堆排序【手写小根堆】
2022-07-06 09:18:00 【小陈同学_】
一、什么是堆呢?
堆是一个高效的优先级队列,我们可以把堆看做一棵完全二叉树的数组。
性质:
- 堆中某个结点的值总是不大于或不小于其父结点的值
- 堆总是一棵完全二叉树
根结点最大的堆叫做最大堆或大根堆,根结点最小的堆叫做最小堆或小根堆。
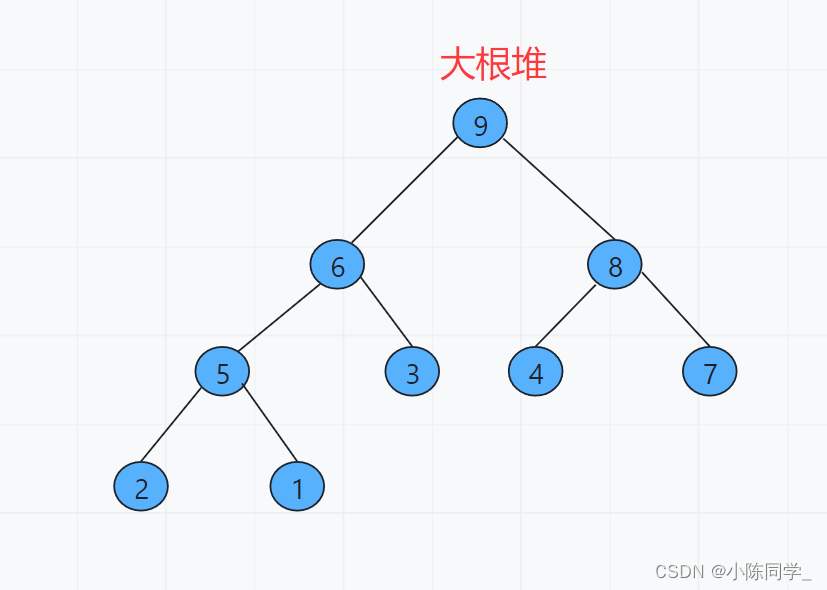
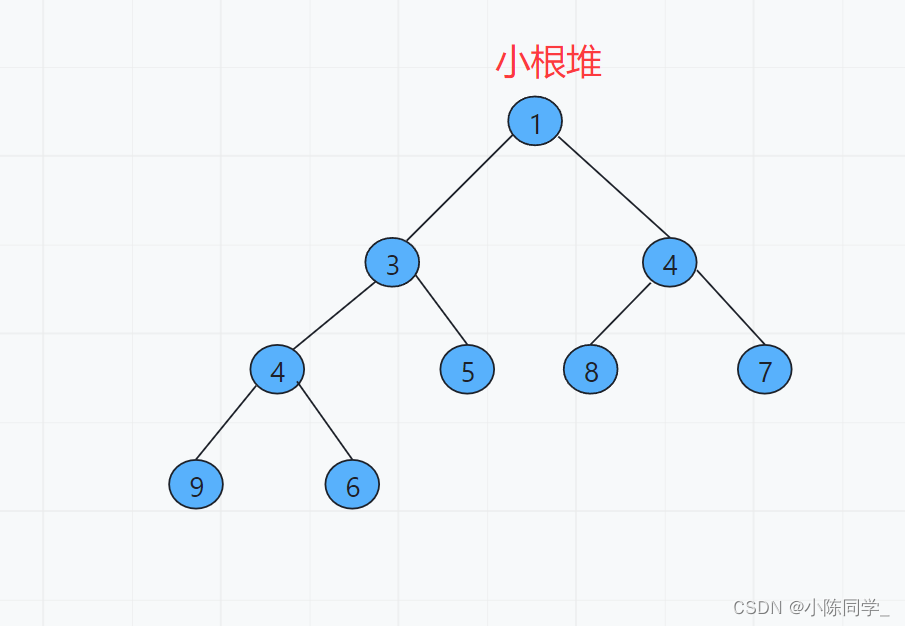
算法思想及操作(小根堆为例):
将要排序的所有值放到一棵完全二叉树的各个结点中,这时候的二叉树不用具备堆的性质,利用up或者down操作来调整堆。
在堆的创建过程中,我们需要加入两个操作:
- 向上调整法(up)【建堆】
从最后一个节点开始调整,跟它的父节点比较,如果比父节点小,则不符合小根堆的性质,因此需要交换,否则不需要交换。
调成完一个节点后,把该节点的父节点看做当前结点,继续做调整。
以此类推,即可调整成堆。 - 向下调整法(down)
设父节点为fa,左儿子为l,右儿子为r。
从最后一个非叶子节点(即第n/2个节点)开始,用fa分别与l和r作比较,最小的儿子做交换,如果fa已经是最小的,则不需要交换。
同向上调整法一样,调整完之后,从最小的儿子当做fa,继续做向下调整法。
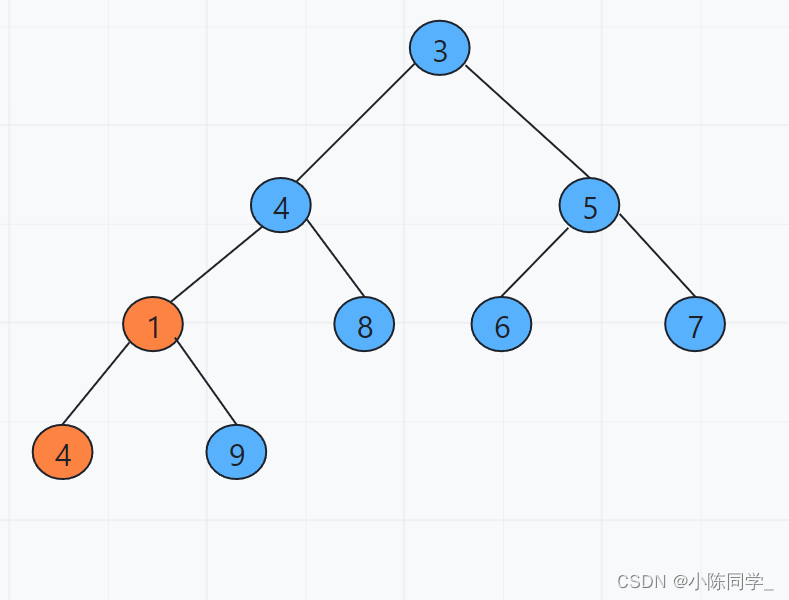
为什么是从最后一个非叶子节点开始down呢?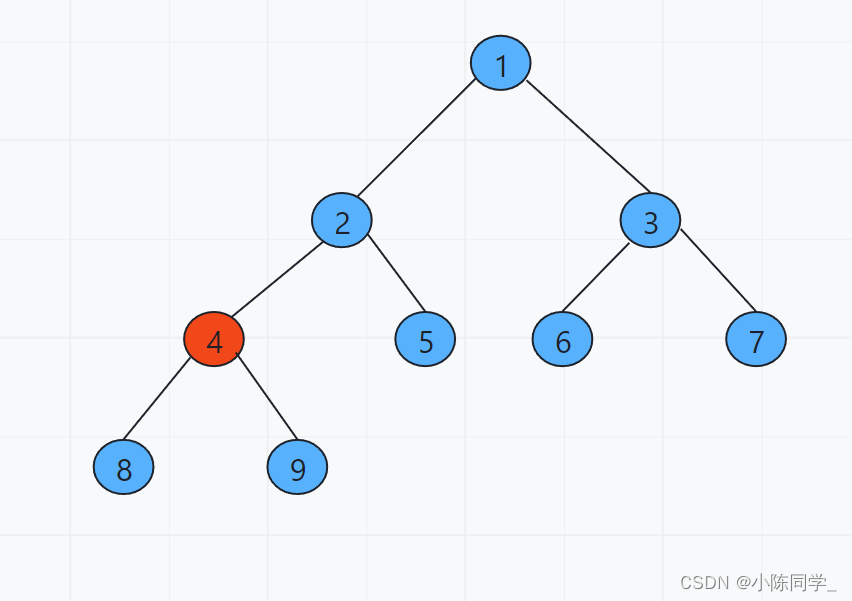
图中的值是节点编号,一共有9个节点,那么n=9,所以从n/2开始调整就是从第四个节点开始调整(红色节点)。
这是为什么呢?
因为我们执行的是down操作,那么为了调整到所有的点,必然要调整到最后一个叶子结点。恰巧最后一个叶子结点的父节点就是第n/2个节点,从n/2个节点开始down,肯定会调整到所有的点。
下面来看一下模拟过程:
初始状态图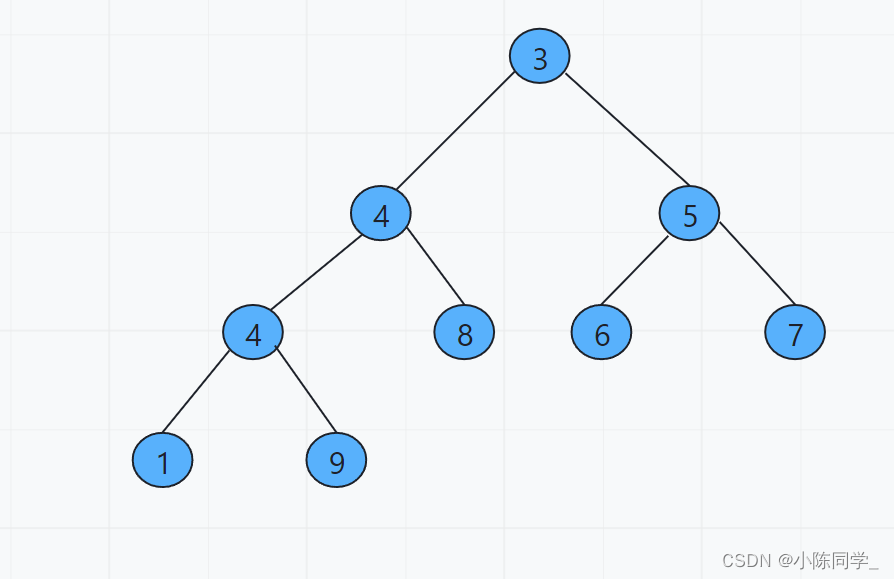
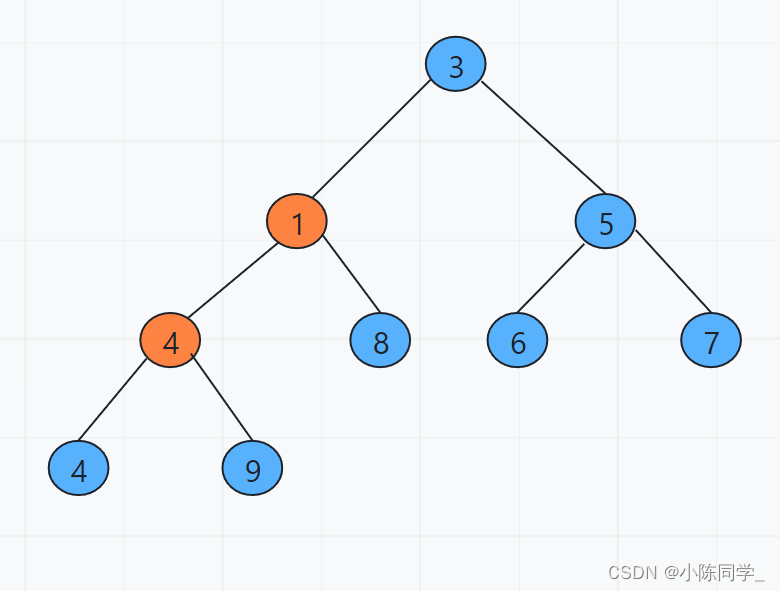
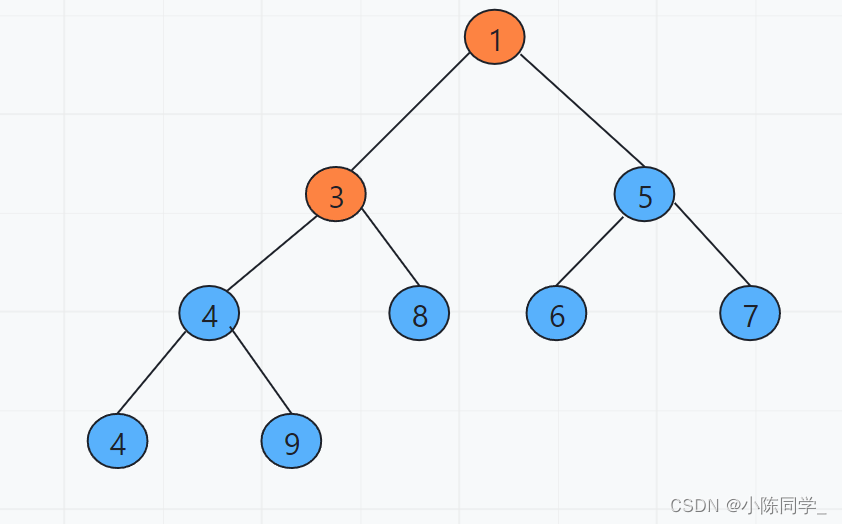
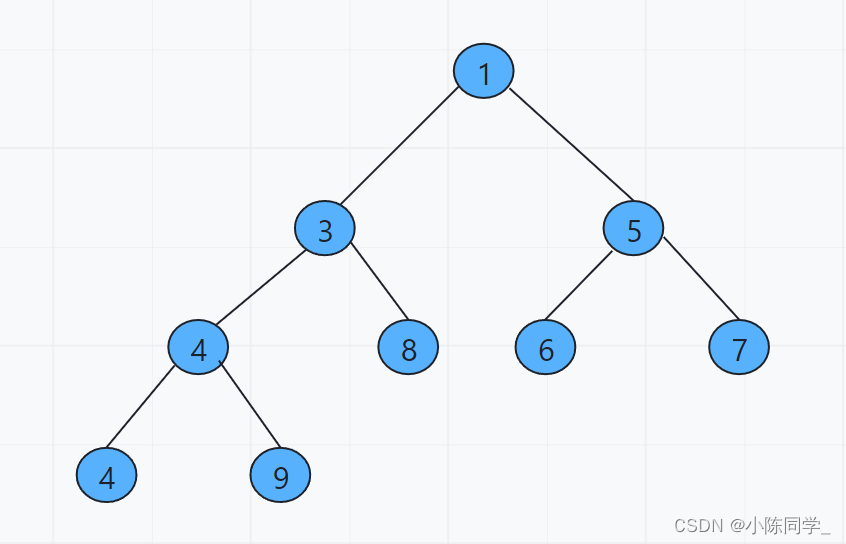
现在就建好了一个小根堆(注意小根堆和大根堆不唯一,满足性质即可)
下面利用堆来排序:
题目:堆排序
输入一个长度为 n n n 的整数数列,从小到大输出前 m m m 小的数。
输入格式
第一行包含整数 n n n 和 m m m。
第二行包含 n 个整数,表示整数数列。
输出格式
共一行,包含 m m m 个整数,表示整数数列中前 m 小的数。
数据范围
1 ≤ m ≤ n ≤ 105 1≤m≤n≤105 1≤m≤n≤105,
1 ≤ 数 列 中 元 素 ≤ 109 1≤数列中元素≤109 1≤数列中元素≤109
输入样例:
5 3
4 5 1 3 2
输出样例:
1 2 3
题目思路:
此题要输出用堆排序后的前k个数,因为堆并不能保证从左到右、从上到下的顺序是依次递增的,比如下图中第三个数为5,实际上第三个数应该为4,所以我们不能建好堆之后直接输出前k个数字。
所以可以利用删除节点(并不是真正意义上的删除)来实现堆排序,删除哪个结点是比较合适的呢,显然不可能是前面和中间的节点,因为在堆中删除前面一个节点是非常麻烦的,但是删除最后一个节点是很容易的。那么删除最后一个节点可不可以呢?答案是可以的,因为堆顶元素保证是最小的一个,所以每次输出了堆顶元素后可以把堆顶元素和最后一个元素交换,此时最小的元素成为了最后一个元素,可以把他删除掉(已经用不到了),然后从堆顶元素开始down操作,因此我们可以发现依然可以维护堆的性质,所以可以利用删除最后一个节点来实现堆的排序。
堆的存储:
为了方便存储以及实现,堆通常可以利用数组来模拟。
fa:父节点,l:左二子,r:右儿子
设 f a = x fa=x fa=x,则 l = 2 ∗ x l=2*x l=2∗x, r = 2 ∗ x + 1 r=2*x+1 r=2∗x+1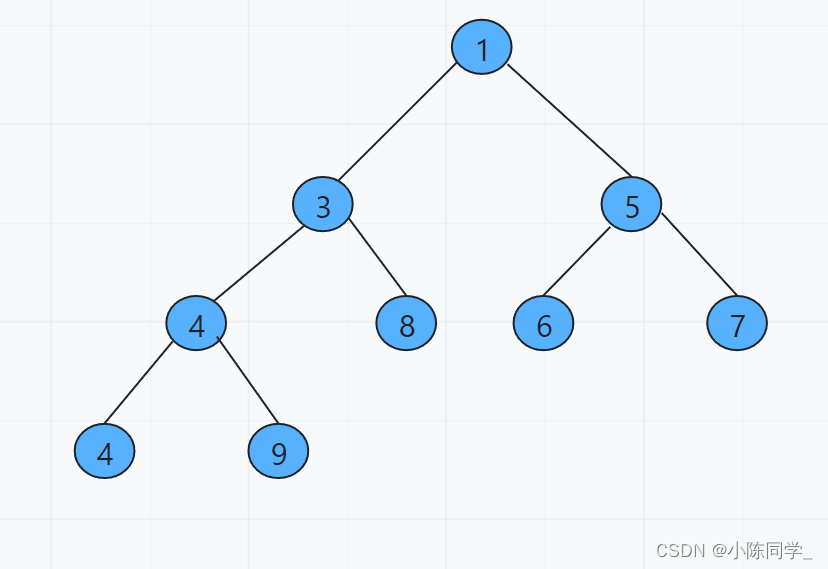
AC代码(C++):
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1e5+10;
int q[N],numbers,n,m;
void down(int x){
int t=x;
if(x*2<=numbers && q[x*2]<q[t]) t=x*2;
if(x*2+1<=numbers && q[x*2+1]<q[t]) t=x*2+1;
if(t!=x){
swap(q[t],q[x]);
down(t);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&q[i]);
numbers=n; //删除一个节点后剩余节点的个数
for(int i=n/2;i;i--) down(i);
while(m--){
printf("%d ",q[1]);
q[1]=q[numbers];
numbers--;
down(1);
}
return 0;
}
边栏推荐
- GPS高程拟合抗差中误差的求取代码实现
- GNSS定位精度指标计算
- Database table splitting strategy
- [offer78] merge multiple ordered linked lists
- Design and implementation of general interface open platform - (39) simple and crude implementation of API services
- (1) Introduction Guide to R language - the first step of data analysis
- 【GNSS数据处理】赫尔默特(helmert)方差分量估计解析及代码实现
- FairyGUI循環列錶
- KF UD分解之伪代码实现进阶篇【2】
- Unity scene jump and exit
猜你喜欢

Latex learning
![[算法] 剑指offer2 golang 面试题10:和为k的子数组](/img/63/7422489d09a64ec9f0e79378761bf1.png)
[算法] 剑指offer2 golang 面试题10:和为k的子数组
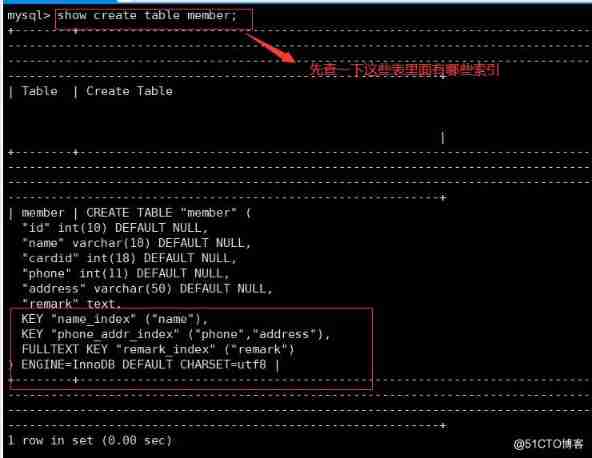
Mysql database index
Matlab读取GNSS 观测值o文件代码示例
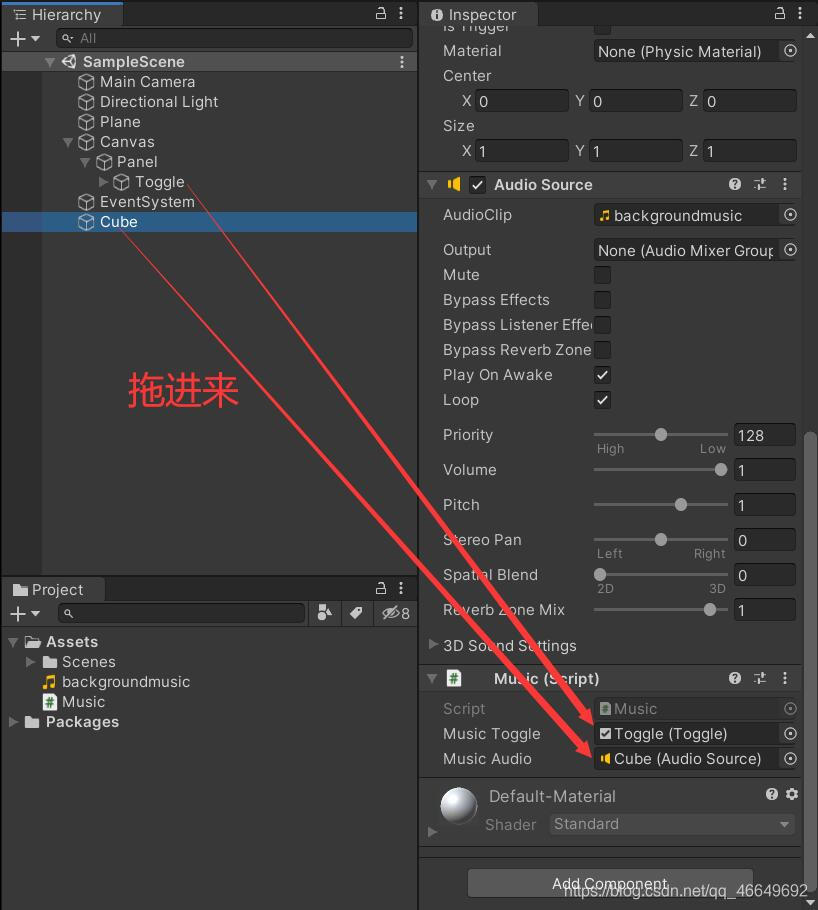
音乐播放(Toggle && PlayerPrefs)

NRF24L01 troubleshooting
First use of dosbox

Vulnhub target: hacknos_ PLAYER V1.1
Teach you to release a DeNO module hand in hand
![[Nodejs] 20. Koa2 onion ring model ----- code demonstration](/img/a8/a4390238685903b63bb036206f8dcb.jpg)
[Nodejs] 20. Koa2 onion ring model ----- code demonstration
随机推荐
FairyGUI簡單背包的制作
Talking about the startup of Oracle Database
基本Dos命令
(3) Introduction to bioinformatics of R language - function, data Frame, simple DNA reading and analysis
Flink late data processing (3)
NovAtel 板卡OEM617D配置步骤记录
[offer29] sorted circular linked list
Containers and Devops: container based Devops delivery pipeline
Itext 7 生成PDF总结
Guided package method in idea
(1) Introduction Guide to R language - the first step of data analysis
[offer18] delete the node of the linked list
Mysql database reports an error: row size too large (> 8126) Changing some columns to TEXT or BLOB or using ROW_ FORMAT=DY
[算法] 剑指offer2 golang 面试题10:和为k的子数组
Combination of fairygui check box and progress bar
Matlab读取GNSS 观测值o文件代码示例
【rtklib】在rtk下使用抗差自适应卡尔曼滤波初步实践
FGUI工程打包发布&导入Unity&将UI显示出来的方式
Unity scene jump and exit
地球围绕太阳转