当前位置:网站首页>【rtklib】在rtk下使用抗差自适应卡尔曼滤波初步实践
【rtklib】在rtk下使用抗差自适应卡尔曼滤波初步实践
2022-07-06 09:18:00 【Proletarians】
一、背景
以前上学的时候做测量,做静态算架站点的坐标做控制或者在校园进行rtk测地形点,都是在视野开阔,运动缓慢的情况下进行。现在使用消费级接收机,在城市动态复杂环境下,例如过天桥、树荫下、高楼旁边,其测量值会出现大量的粗差和周跳的现象,很是频繁,影响到了量测模型;同时,载体的运动状态也是不清楚的,例如,在路口拐弯,遇到行人车要减速,绿灯后车要加速等,影响到了动力学模型。
鉴于以上描述的函数模型两方面,那么在使用ekf的时候,心里就慌慌了。这个时候考虑使用抗差自适应卡尔曼滤波,一是抗差估计调整量测噪声矩阵,二是自适应调整动力学模型,平衡两者的贡献。
二、vs后处理实践
在rtklib中,我们在进行vs后处理post的时候,如果使用了伽利略、glonass等,要注意在头文件中定义系统的宏,否则得到的只是gps的rtk结果。既然是动态rtk,那么接收机的dynamic选项要打开,这在配置文件可以直接更改。下面要分两步来进行,自适应因子的确定和抗差估计得到的量测噪声矩阵。
2.1 自适应因子的确定
自适应因子的确定可以从两方面,一是新息向量,也就是通过一步预测值和测量值得到的,是第一次ddres得到的v;二是通过状态不符值,即通过当前时刻的状态向量和一步预测值的模。
在实际使用中,不建议使用状态不符值,因为这个状态有时算出来相差太大,新息向量更能反映动态系统的扰动。
示例代码如下:
/* adaptive factor resolved by predicted residual */
static double adaptive_factor(const double *v, int nv)
{
double sum = 0.0,ret;
double c0 = 1.5, c1 = 8.0;
for (int i = 0; i < nv; i++) {
sum += v[i] * v[i];
}
sum = sqrt(sum);
if (sum>c1)
{
ret = 0;
}
else if(sum <= c0) {
ret = 1;
}
else {
ret = (c0 / sum)*SQRT((c1 - sum) / (c1 - c0));
}
return ret;
}
2.2 抗差M估计
抗差估计是使用验后测量残差进行计算得到的,rtk双差测量值是相关的,那么在进行抗差估计的时候就不能使用等价权策略了,参考了刘经南的计算方法,和杨元喜的双因子模型其实是一回事。
示例代码如下:
/* 抗差估计算法,RTK双差观测值之间相关,不能采用等价权方案 */
/* v I 验后观测残差向量 */
/* R I 量测噪声方差-协方差阵 */
/* vflag I 双差卫星新息字段 */
/* nv I 量测噪声方差-协方差阵维数 即R大小为(nv*nv) */
static double * robust_estimate(const double *v, const double *R, const int *vflg, int nv)
{ // nv表示量测噪声方差-协方差阵R的维数,RTK的量测噪声矩阵R是相关的,需要确定等价方差-协方差矩阵R_,参考刘经南计算方法
int i, j, sat1, sat2, type, freq;
double *R_;
double w,c=2.0,p; // w表示标准化残差,c~[1.5,3.0],p表示相关系数
R_ = mat(nv, nv);
// step1 先保存对角线元素
for (i = 0; i < nv; i++) {
w = 0.0;
sat1 = (vflg[i] >> 16) & 0xFF;
sat2 = (vflg[i] >> 8) & 0xFF;
type = (vflg[i] >> 4) & 0xF; // type == 0 ? "L" : (type == 1 ? "P" : "C")
freq = vflg[i] & 0xF;
// 验后观测残差的标准化残差
w = fabs(v[i]) / R[i + i*nv];
R_[i + i*nv] = (w < c) ? R[i + i*nv] : w*w*R[i + i*nv];
}
// step2 再填充非对角线元素,使用相关系数p来填充R_
for (i = 0; i < nv; i++) {
for (j = 0; j < nv; j++) {
if (i == j) continue;
p = R[j + i*nv] / (sqrt(R[i + i*nv] * R[j + j*nv]));
R_[j + i*nv] = p*sqrt(R_[i + i*nv] * R_[j + j*nv]);
}
}
return R_;
}
注释中描述了步骤,但是这个策略中没有对ddpr和ddcp进行分开处理,是要分开处理的,因为ddcp的时候有可能是周跳没剔除干净导致的,那么模糊度就要重置,只是把这个代码流程放出来,大家当个参考吧。
2.3 其他注意
得到了自适应因子,在卡尔曼滤波filter函数中k的计算只需要在控制系数的那儿由1.0变成1.0/factor即可。
当前历元计算的状态向量的Pp,我加了这个
if (!(info=matinv(Q,m))) {
matmul("NN",n,m,m,1.0,F,Q,0.0,K); /* K=P*H*Q^-1 */
matmul("NN",n,1,m,1.0,K,v,1.0,xp); /* xp=x+K*v */
matmul("NT",n,n,m,-1.0,K,H,1.0,I); /* Pp=(I-K*H')*P */
matmul("NN",n,n,n,1.0,I,P,0.0,Pp);
// 张友民
//matmul("NT", n, n, n, 1.0, Pp, I, 0.0, Pp);
//matmul("NT", m, n, m, 1.0, R, K, 0.0, F_);
//matmul("NN", n, n, m, 1.0, K, F_, 1.0, Pp);
}
result
结果测试的不好啊,怎么放出来,哈哈哈。只是给大家提供一个思路~
边栏推荐
- How to improve the deletion speed of sequential class containers?
- dosbox第一次使用
- 單片機藍牙無線燒錄
- InnoDB dirty page refresh mechanism checkpoint in MySQL
- Walk into WPF's drawing Bing Dwen Dwen
- Gateway 根据服务名路由失败,报错 Service Unavailable, status=503
- 基於Redis的分布式ID生成器
- Unity场景跳转及退出
- Introduction to the daily practice column of the Blue Bridge Cup
- Unity3D,阿里云服务器,平台配置
猜你喜欢

NRF24L01 troubleshooting

(三)R语言的生物信息学入门——Function, data.frame, 简单DNA读取与分析
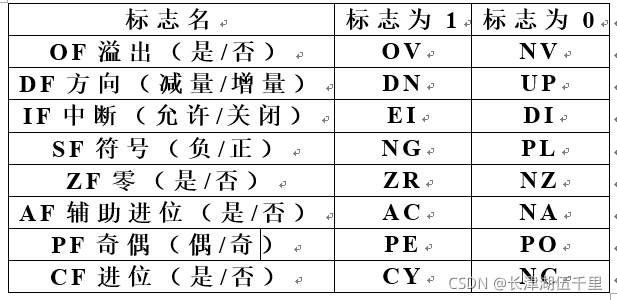
2021.11.10汇编考试
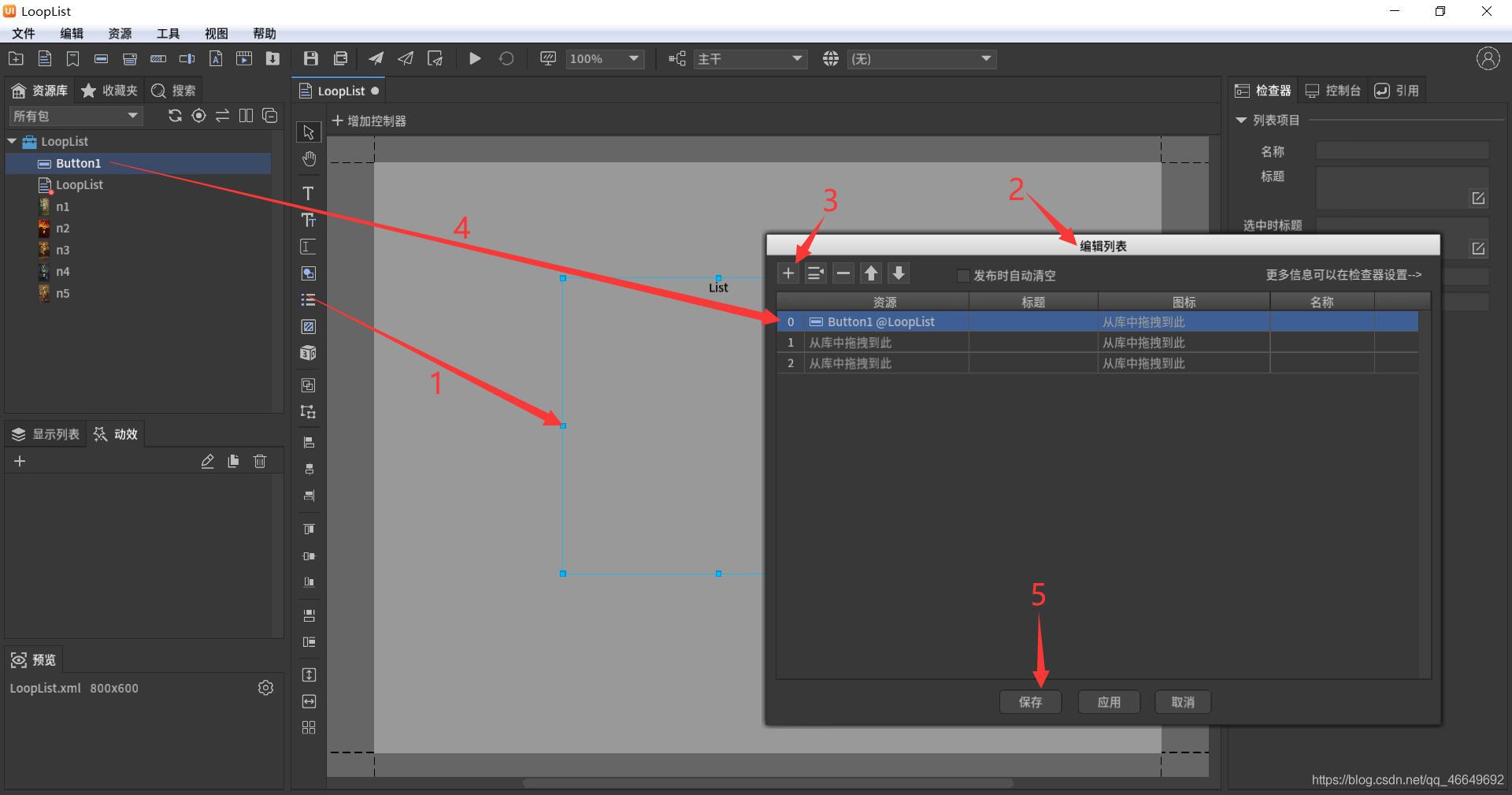
FairyGUI循环列表

基於Redis的分布式ID生成器
编译原理:源程序的预处理及词法分析程序的设计与实现(含代码)

Naive Bayesian theory derivation
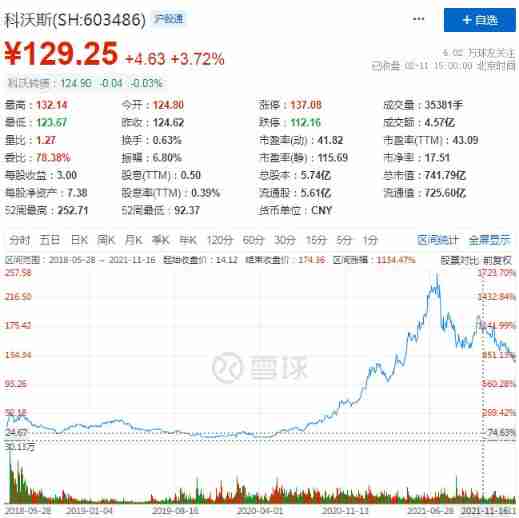
The service robots that have been hyped by capital and the Winter Olympics are not just a flash in the pan
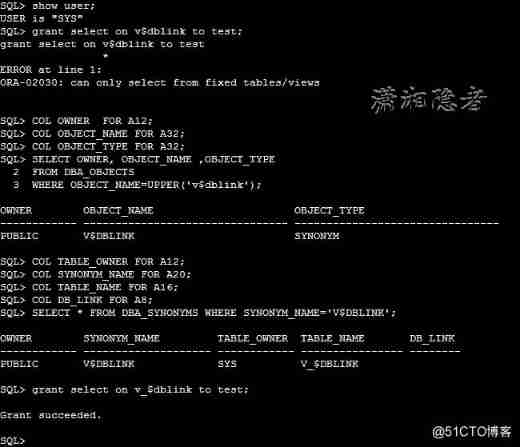
ORA-02030: can only select from fixed tables/views

Latex learning
随机推荐
(四)R语言的数据可视化——矩阵图、柱状图、饼图、散点图与线性回归、带状图
Idea problem record
Solution to the problem of automatic login in Yanshan University Campus Network
Fabrication d'un sac à dos simple fairygui
1041 be unique (20 points (s)) (hash: find the first number that occurs once)
MySQL takes up too much memory solution
First use of dosbox
[offer78] merge multiple ordered linked lists
[Leetcode15]三数之和
FairyGUI循環列錶
Intermediate use tutorial of postman [environment variables, test scripts, assertions, interface documents, etc.]
[899] ordered queue
Derivation of logistic regression theory
Servlet
基于rtklib源码进行片上移植的思路分享
[899]有序队列
(3) Introduction to bioinformatics of R language - function, data Frame, simple DNA reading and analysis
Redis cache update strategy, cache penetration, avalanche, breakdown problems
Theoretical derivation of support vector machine
Who says that PT online schema change does not lock the table, or deadlock