当前位置:网站首页>Pytorch: tensor operation (I) contiguous
Pytorch: tensor operation (I) contiguous
2022-07-06 12:13:00 【harry_ tea】
Contents of this article
tensor Storage in memory
Information area and storage area
tensor The storage in memory contains Information area and Storage area
- Information area (Tensor) contain tensor The shape of the size, step stride, data type type etc.
- Storage area (Storage) Contains stored data
High dimensional arrays are stored in memory according to row priority , What is row priority ? Suppose we have a (3, 4) Of tensor, It is actually stored as a one-dimensional array , But in tensor The information area of recorded his size and stride As a result, the array actually displayed is two-dimensional ,size by (3, 4)
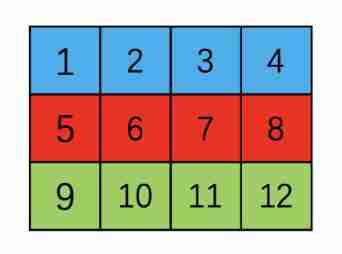
Two dimensional array

One dimensional form in memory
Now let's look at an example , Examples show that tensor The elements in are contiguous in memory , And it also proves that it is indeed row priority storage
tensor = torch.tensor([[[1 ,2, 3, 4], [5, 6, 7, 8], [9, 10,11,12]],
[[13,14,15,16],[17,18,19,20],[21,22,23,24]]])
print(tensor.is_contiguous())
for i in range(2):
for j in range(3):
for k in range(4):
print(tensor[i][j][k].data_ptr(), end=' ')
''' True 140430616343104 140430616343112 140430616343120 140430616343128 140430616343136 140430616343144 140430616343152 140430616343160 140430616343168 140430616343176 140430616343184 140430616343192 140430616343200 140430616343208 140430616343216 140430616343224 140430616343232 140430616343240 140430616343248 140430616343256 140430616343264 140430616343272 140430616343280 140430616343288 '''
shape && stride
Continuing with the above example, let's take a look at shape and stride attribute , about (2, 3, 4) Dimensional tensor His shape by (2, 3 ,4),stride by (12, 4, 1)
shape
shape It's easy to understand , Namely tensor Dimensions , The above example is (2, 3, 4) Of tensor, Dimension is (2, 3, 4)
stride
stride Represents the step size of multidimensional index , Each step represents an offset in memory +1, about (2, 3, 4) Dimensional tensor:stride+1 Represents the (dim2)+1,stride+4 For the rest dim unchanged ,(dim1)+1,stride+12 For the rest dim unchanged ,(dim0)+1, As shown in the figure below
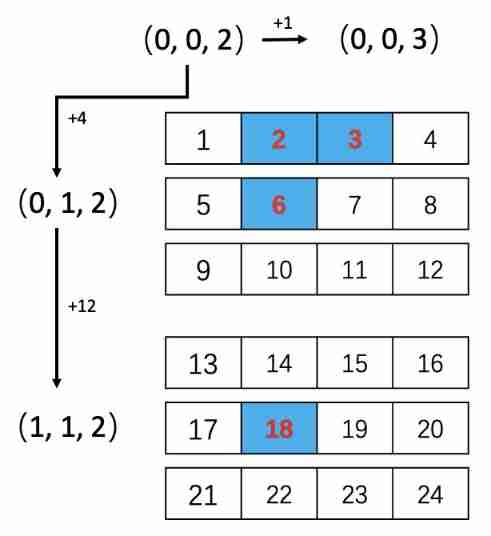
Icon stride
stride computing method
s t r i d e i = s t r i d e i + 1 ∗ s i z e i + 1 i ∈ [ 0 , n − 2 ] stride_{i} = stride_{i+1} * size_{i+1}~~~~i\in[0, n-2] stridei=stridei+1∗sizei+1 i∈[0,n−2]
about shape(2, 3, 4) Of tensor, The calculation is as follows (stride3=1)
s t r i d e 2 = s t r i d e 3 ∗ s h a p e 3 = 1 ∗ 4 = 4 s t r i d e 1 = s t r i d e 2 ∗ s h a p e 2 = 4 ∗ 3 = 12 stride_{2} = stride_{3} * shape_{3}=1*4=4 \\ stride_{1} = stride_{2} * shape_{2}=4*3=12 stride2=stride3∗shape3=1∗4=4stride1=stride2∗shape2=4∗3=12
stride = [1] # Initialize the first element
# Iterate back and forward to generate stride
for i in range(len(tensor.size())-2, -1, -1):
stride.insert(0, stride[0] * tensor.shape[i+1])
print(stride) # [12, 4, 1]
print(tensor.stride()) # (12, 4, 1)
I understand tensor After storage in memory , Let's see contiguous
contiguous
contiguous
Returns a continuous memory tensor
Returns a contiguous in memory tensor containing the same data as self tensor. If self tensor is already in the specified memory format, this function returns the self tensor.
When to use contiguous Well ?
The simple understanding is tensor Use when the storage order in the memory address is inconsistent with the actual one-dimensional index order , As shown below , Right up there tensor One dimensional index , The result is [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12], Original tensor Application transpose To transpose , In the one-dimensional index , The result is [1, 5, 9, 2, 6, 10, 3, 7, 11, 4, 8, 12], At this time, the index order changes , So we need to use contiguous
Be careful : No matter how it changes, the corresponding address of each element is unchanged , such as 11 The corresponding address is x11,transpose after 11 Still corresponding x11, So what has changed ? Remember tensor Is it divided into information area and storage area , The storage area does not change , What changes is the information area shape,stride Etc , Make an introduction when you have time ~
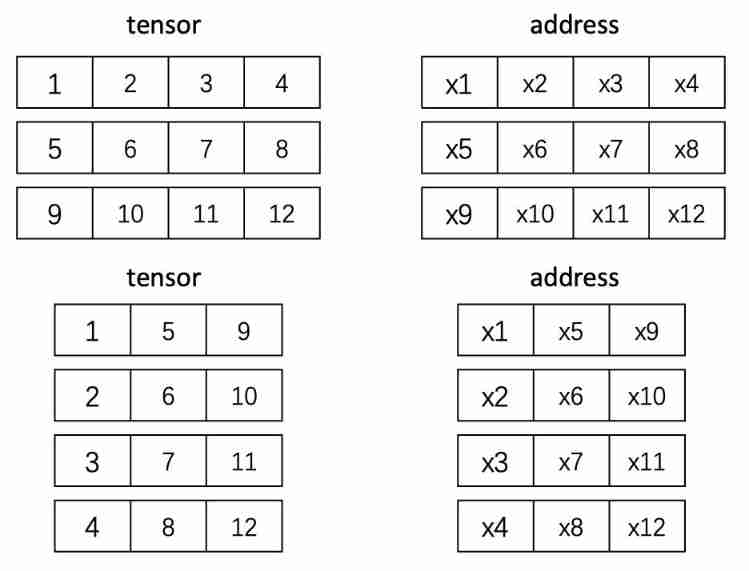
Code example
tensor = torch.tensor([[1,2,3,4],[5,6,7,8],[9,10,11,12]])
print(tensor)
print(tensor.is_contiguous())
tensor = tensor.transpose(1, 0)
print(tensor)
print(tensor.is_contiguous())
''' tensor([[ 1, 2, 3, 4], [ 5, 6, 7, 8], [ 9, 10, 11, 12]]) True tensor([[ 1, 5, 9], [ 2, 6, 10], [ 3, 7, 11], [ 4, 8, 12]]) False '''
Why use contiguous
Some people may have questions , Since the above index is different from before ( It's not continuous ), Why make him continuous ? because pytorch Some operations of require index and memory continuity , such as view
Code example ( Next, let's take the example above )
tensor = tensor.contiguous()
print(tensor.is_contiguous())
tensor = tensor.view(3, 4)
print(tensor)
''' True tensor([[ 1, 5, 9, 2], [ 6, 10, 3, 7], [11, 4, 8, 12]]) '''
If not contiguous The following errors will be reported
RuntimeError: view size is not compatible with input tensor's size and stride (at least one dimension spans across two contiguous subspaces). Use .reshape(...) instead.
Why? contiguous It works ?
contiguous In a simple and crude way , Since your previous index and memory are not continuous , Then I'll reopen a piece of continuous memory and index it
Code example , From the following code stride Changes can be seen ,transpose After that tensor It really changes the information in the information area
tensor = torch.tensor([[1,2,3,4],[5,6,7,8],[9,10,11,12]])
print(tensor.is_contiguous()) # True
for i in range(3):
for j in range(4):
print(tensor[i][j], tensor[i][j].data_ptr(), end=' ')
print()
print(tensor.stride()) # (4, 1)
''' True tensor(1) 140430616321664 tensor(2) 140430616321672 tensor(3) 140430616321680 tensor(4) 140430616321688 tensor(5) 140430616321696 tensor(6) 140430616321704 tensor(7) 140430616321712 tensor(8) 140430616321720 tensor(9) 140430616321728 tensor(10) 140430616321736 tensor(11) 140430616321744 tensor(12) 140430616321752 (4, 1) '''
tensor = tensor.transpose(1, 0)
print(tensor.is_contiguous()) # False
for i in range(4):
for j in range(3):
print(tensor[i][j], tensor[i][j].data_ptr(), end=' ')
print()
print(tensor.stride()) # (1, 4) changed
''' False tensor(1) 140430616321664 tensor(5) 140430616321696 tensor(9) 140430616321728 tensor(2) 140430616321672 tensor(6) 140430616321704 tensor(10) 140430616321736 tensor(3) 140430616321680 tensor(7) 140430616321712 tensor(11) 140430616321744 tensor(4) 140430616321688 tensor(8) 140430616321720 tensor(12) 140430616321752 (1, 4) '''
tensor = tensor.contiguous()
print(tensor.is_contiguous()) # True
for i in range(4):
for j in range(3):
print(tensor[i][j], tensor[i][j].data_ptr(), end=' ')
print()
print(tensor.stride()) # (3, 1)
''' True tensor(1) 140431681244608 tensor(5) 140431681244616 tensor(9) 140431681244624 tensor(2) 140431681244632 tensor(6) 140431681244640 tensor(10) 140431681244648 tensor(3) 140431681244656 tensor(7) 140431681244664 tensor(11) 140431681244672 tensor(4) 140431681244680 tensor(8) 140431681244688 tensor(12) 140431681244696 (3, 1) '''
边栏推荐
- Générateur d'identification distribué basé sur redis
- C语言函数之可变参数原理:va_start、va_arg及va_end
- Comparison of solutions of Qualcomm & MTK & Kirin mobile platform USB3.0
- C语言,log打印文件名、函数名、行号、日期时间
- A possible cause and solution of "stuck" main thread of RT thread
- Arduino uno R3 register writing method (1) -- pin level state change
- JS正则表达式基础知识学习
- Cannot change version of project facet Dynamic Web Module to 2.3.
- Learning notes of JS variable scope and function
- E-commerce data analysis -- salary prediction (linear regression)
猜你喜欢

Apprentissage automatique - - régression linéaire (sklearn)
arduino JSON数据信息解析
open-mmlab labelImg mmdetection

基於Redis的分布式ID生成器
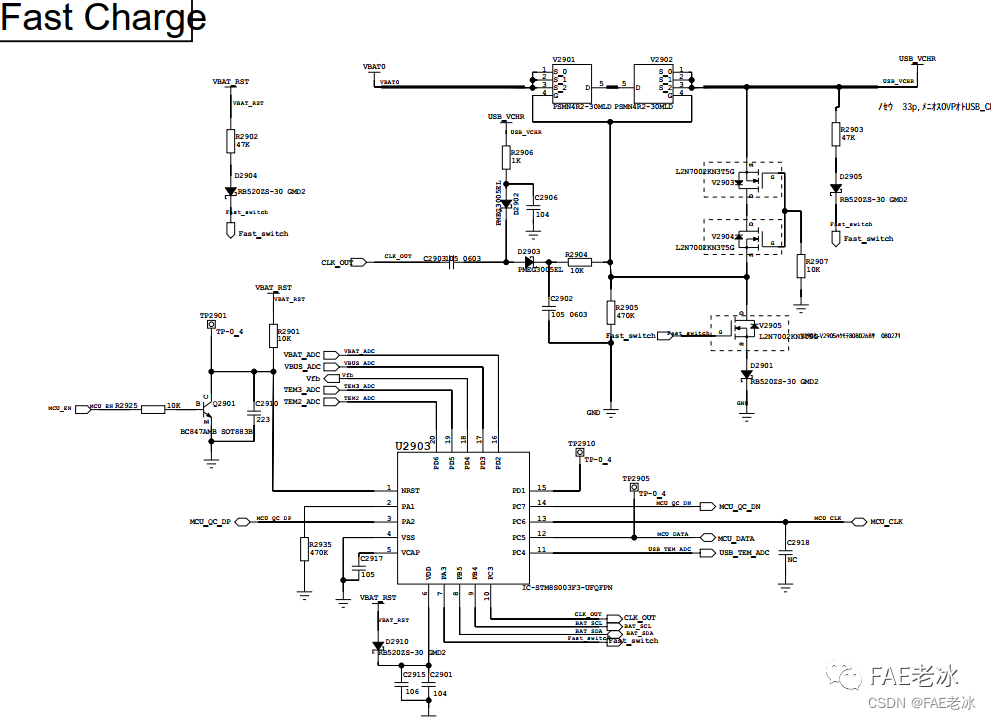
OPPO VOOC快充电路和协议

Gallery's image browsing and component learning
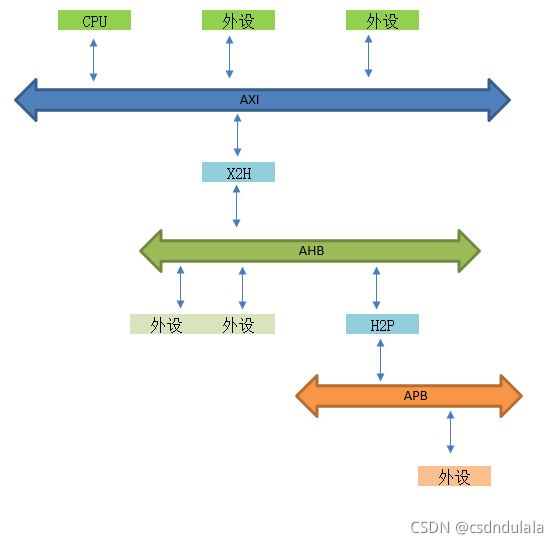
AMBA、AHB、APB、AXI的理解

RT thread API reference manual
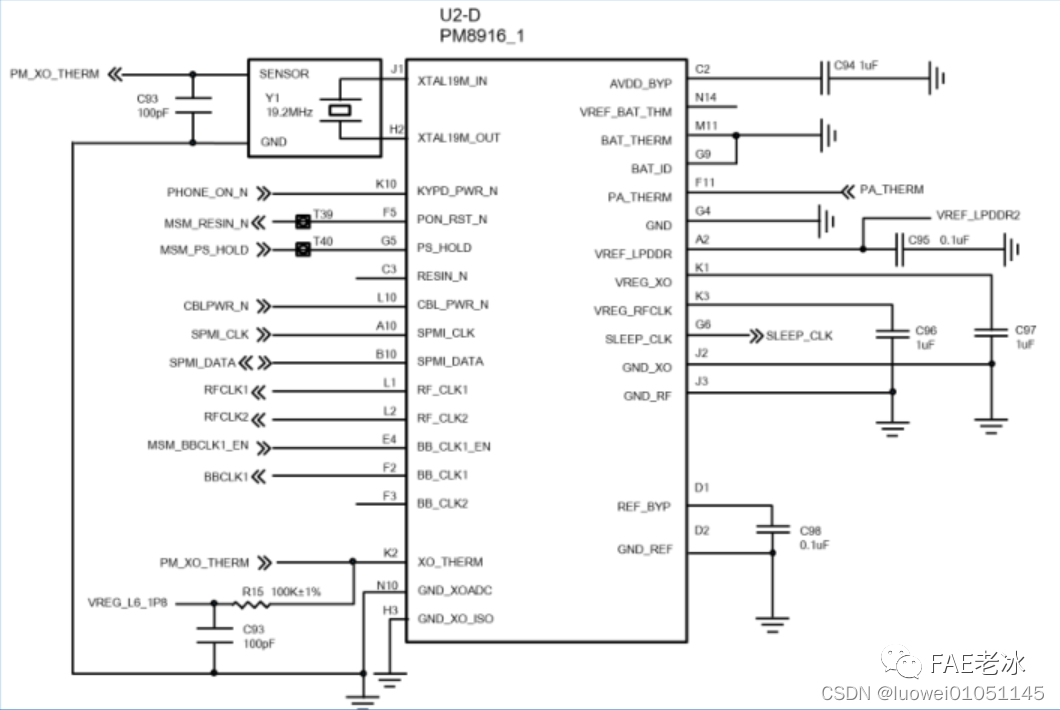
Working principle of genius telephone watch Z3
Types de variables JS et transformations de type communes
随机推荐
Time slice polling scheduling of RT thread threads
ES6 grammar summary -- Part 2 (advanced part es6~es11)
MySQL takes up too much memory solution
. elf . map . list . Hex file
Keyword inline (inline function) usage analysis [C language]
Oppo vooc fast charging circuit and protocol
Whistle+switchyomega configure web proxy
PT OSC deadlock analysis
I2C总线时序详解
Togglebutton realizes the effect of switching lights
2022.2.12 resumption
Kaggle竞赛-Two Sigma Connect: Rental Listing Inquiries
arduino UNO R3的寄存器写法(1)-----引脚电平状态变化
ESP学习问题记录
数据分析之缺失值填充(重点讲解多重插值法Miceforest)
arduino获取随机数
基於Redis的分布式ID生成器
Redis based distributed ID generator
Selective sorting and bubble sorting [C language]
STM32 如何定位导致发生 hard fault 的代码段