当前位置:网站首页>Apprentissage automatique - - régression linéaire (sklearn)
Apprentissage automatique - - régression linéaire (sklearn)
2022-07-06 11:53:00 【Je veux être un cerf - volant.】
Apprentissage automatique–Modèle de régression linéaire(sklearn)
Modèle de régression linéaireOui.:En généralRégression linéaire unidimensionnelleEtRégression linéaire multiple,UtiliserL2NormalRetour en montagne(Ridge),UtiliserL1NormalRégression lasso(Lasso),UtiliserL1EtL2NormalElasticNetRetour(C'est vrai.LassoLa fusion du retour et du retour de la crête),Régression logique.
Régression linéaire-sklearnMéthode d'appel de la bibliothèque et explication des paramètres:
from sklearn.linear_model import LinearRegression
LinearRegression(fit_intercept=True,normalize=False,copy_X=True,n_jobs=1)
Signification des paramètres:
- fit_intercept:Booléen,Indique si l'interception dans la régression linéaire doit être calculée,C'est - à - dire:bValeur.Si ouiFalse,Pas de calcul.b Valeur.
- normalize:Booléen.Si ouiFalse,L'échantillon d'entraînement sera normalisé.
- copy_X:Booléen.Si ouiTrue,Une copie des données de formation sera copiée.
- n_jobs:Un entier. Spécifié lorsque la tâche est parallèle CPUNombre.Si la valeur est-1 Utilisez tous les CPU.
Propriétés
- coef_:Vecteur de poids
- intercept_:InterceptionbValeur
Méthodes:
- fit(X,y):Modèle d'entraînement.
- predict(X):Prédiction à l'aide d'un modèle bien formé, Et renvoie la valeur prévue .
- score(X,y): Renvoie le score du rendement prévu .
La formule de calcul est:: s c o r e = ( 1 − u / v ) score=(1 - u/v) score=(1−u/v)
Parmi eux u = ( ( y t r u e − y p r e d ) ∗ ∗ 2 ) . s u m ( ) , v = ( ( y t r u e − y t r u e . m e a n ( ) ) ∗ ∗ 2 ) . s u m ( ) u=((y_true - y_pred) ** 2).sum(),v=((y_true - y_true.mean()) ** 2).sum() u=((ytrue−ypred)∗∗2).sum(),v=((ytrue−ytrue.mean())∗∗2).sum()
scoreLa valeur maximale est1, Mais ça pourrait être négatif ( Les prévisions sont trop mauvaises ).scorePlus grand., Meilleure performance prédictive .
AdhésionL2Régression linéaire régularisée-sklearnMéthode d'appel de la bibliothèque et explication des paramètres
from sklearn.linear_model import Ridge
Ridge(alpha=1.0, fit_intercept=True, normalize=False,copy_X=True, max_iter=None,
tol=1e-3, solver=“auto”,random_state=None)
Signification des paramètres:
alpha:Coefficient du terme régulier, Plus la valeur est élevée, plus la proportion de termes réguliers est élevée. . La valeur initiale est recommandée pour commencer à 0, Alors assurez - vous d'avoir une meilleure étude Taux, Une fois le taux d'apprentissage établi ,Voilà.alpha Une petite valeur , Ensuite, selon la précision de l'ensemble de vérification ,Augmentation ou diminution10X.10 Double grossier , Lorsque l'ordre de grandeur approprié a été déterminé , Ajuster finement dans le même ordre de grandeur .
fit_intercept:Booléen, Indique si l'interception doit être calculée bValeur.FalseNe calcule pasbValeur.
normalize:Booléen.Si égal àTrue, Les données sont normalisées avant la formation au modèle . La normalisation présente deux avantages : (1):Augmenter le taux de convergence du modèle, Réduire le temps de recherche de la solution optimale . (2) Améliorer la précision du modèle .
copy_X:Booléen.Si défini àTrue, Une copie des données de formation sera copiée .
max_iter:Entier. Nombre maximum d'itérations spécifiées .Si ouiNone,Par défaut.
tol:Seuil. Déterminer si l'itération converge ou satisfait aux exigences de précision .
solver:String. Spécifier un algorithme pour résoudre le problème d'optimisation .
(1).solver=‘auto’, Algorithme de sélection automatique basé sur l'ensemble de données .
(2).solver=‘svd’, Calcul par décomposition de la valeur singulière
(3).solver=‘cholesky’,Adoptionscipy.linalg.solve Fonction pour résoudre la solution optimale .
(4).solver=‘sparse_cg’,Adoptionscipy.sparse.linalg.cg Fonction pour trouver la solution optimale .
(5).solver=‘sag’,AdoptionStochastic Average Gradient descent Algorithme pour résoudre le problème d'optimisation .random_state: Un entier ou un RandomStateExemple,Ou pourNone.Il est là.solver="sag"À utiliser.
(1).Si c'est un entier, Il spécifie la graine du générateur de nombres aléatoires .
(2).Si ouiRandomStateExemple, Un générateur de nombres aléatoires est spécifié .
(3).Si ouiNone, Le générateur de nombres aléatoires par défaut est utilisé .
Propriétés:
- coef_:Vecteur de poids.
- intercept_:InterceptionbValeur de.
- n_iter_:Nombre réel d'Itérations.
Méthodes:
- fit(X,y):Modèle d'entraînement.
- predict(X): Avec des modèles bien formés pour prédire , Et renvoie la valeur prévue .
- score(X,y): Renvoie le score du rendement prévu .
La formule de calcul est:: s c o r e = ( 1 − u / v ) score=(1 - u/v) score=(1−u/v)
Parmi eux u = ( ( y t r u e − y p r e d ) ∗ ∗ 2 ) . s u m ( ) , v = ( ( y t r u e − y t r u e . m e a n ( ) ) ∗ ∗ 2 ) . s u m ( ) u=((y_true - y_pred) ** 2).sum(),v=((y_true - y_true.mean()) **2).sum() u=((ytrue−ypred)∗∗2).sum(),v=((ytrue−ytrue.mean())∗∗2).sum()
scoreLa valeur maximale est1, Mais ça pourrait être négatif ( Les prévisions sont trop mauvaises ).scorePlus grand., Meilleure performance prédictive .
AdhésionL1Régression linéaire régularisée-sklearnMéthode d'appel de la bibliothèque et explication des paramètres
from sklearn.linear_model import Lasso
Lasso(alpha=1.0, fit_intercept=True, normalize=False, precompute=False,
copy_X=True, max_iter=1000,
tol=1e-4, warm_start=False, positive=False,random_state=None,
selection=‘cyclic’)
Signification des paramètres:
- alpha: Coefficient du terme de régularisation
- fit_intercept:Booléen, Indique si l'interception doit être calculée bValeur.FalseNe calcule pasbValeur.
- max_iter: Spécifiez le nombre maximum d'itérations .
- normalize:Booléen.Si égal àTrue, Les données sont normalisées avant la formation au modèle . La normalisation présente deux avantages : (1):Augmenter le taux de convergence du modèle, Réduire le temps de recherche de la solution optimale . (2) Améliorer la précision du modèle .
- precompute: Une valeur booléenne ou une séquence . Il détermine si le calcul est effectué à l'avance Gram Matrice pour accélérer le calcul .
- tol:Seuil. Déterminer si l'itération converge ou satisfait aux exigences de précision .
- warm_start:Booléen.Si ouiTrue, Alors Continuez avec les résultats de votre entraînement précédent . Sinon, commencez l'entraînement dès le début .
- positive:Booléen.Si ouiTrue, Ensuite, les composantes du vecteur de poids doivent être positives. .
- selection:String,C'est possible."cyclic"Ou"random". Il spécifie que chaque itération , Choisissez lequel des vecteurs de poids Composant pour mettre à jour .
(1)“random”:Mise à jour, Sélectionnez au hasard une composante du vecteur de poids à mettre à jour .
(2)“cyclic”:Mise à jour, Sélectionnez un composant du vecteur de poids de l'avant à l'arrière pour mettre à jour - random_state: Un entier ou un RandomStateExemple,OuNone.
(1):Si c'est un entier, Il spécifie la graine du générateur de nombres aléatoires .
(2):Si ouiRandomStateExemple, Il spécifie le générateur de nombres aléatoires .
(3):Si ouiNone, Le générateur de nombres aléatoires par défaut est utilisé .
Propriétés:
- coef_:Vecteur de poids.
- intercept_:InterceptionbValeur.
- n_iter_:Nombre réel d'Itérations.
Méthodes:
- fit(X,y):Modèle d'entraînement.
- predict(X):Prévision à l'aide d'un modèle,Retour à la prévision.
- score(X,y): Renvoie le score du rendement prévu .
La formule de calcul est:: s c o r e = ( 1 − u / v ) score=(1 - u/v) score=(1−u/v)
Parmi eux u = ( ( y t r u e − y p r e d ) ∗ ∗ 2 ) . s u m ( ) , v = ( ( y t r u e − y t r u e . m e a n ( ) ) ∗ ∗ 2 ) . s u m ( ) u=((y_true - y_pred) ** 2).sum(),v=((y_true - y_true.mean()) ** 2).sum() u=((ytrue−ypred)∗∗2).sum(),v=((ytrue−ytrue.mean())∗∗2).sum()
scoreLa valeur maximale est1, Mais ça pourrait être négatif ( Les prévisions sont trop mauvaises ).scorePlus grand., Meilleure performance prédictive .
ElasticNet Le retour est juste. LassoLa fusion du retour et du retour de la crête, Son terme de régularisation est L1Somme des normesL2 Un compromis entre les normes .-sklearnMéthode d'appel de la bibliothèque et explication des paramètres
Le terme de régularisation est: a l p h a ∗ l 1 r a t i o ∗ ∣ ∣ w ∣ ∣ 1 + 0.5 ∗ a l p h a ∗ ( 1 − l 1 r a t i o ) ∗ ∣ ∣ w ∣ ∣ 2 2 alpha * l1_ratio * ||w||_1 + 0.5 * alpha * (1 - l1_ratio) * ||w||^2_2 alpha∗l1ratio∗∣∣w∣∣1+0.5∗alpha∗(1−l1ratio)∗∣∣w∣∣22
from sklearn.linear_model import ElasticNet
ElasticNet(alpha=1.0, l1_ratio=0.5, fit_intercept=True,
normalize=False,precompute=False, max_iter=1000,copy_X=True, tol=1e-4,
warm_start=False, positive=False,random_state=None, selection=‘cyclic’)
Signification des paramètres:
- alpha: Dans la régularisation alphaValeur.
- l1_ratio: Dans le terme de régularisation l1_ratioValeur.
- fit_intercept:Booléen, Indique si l'interception doit être calculée bValeur.FalseNe calcule pasbValeur.
- max_iter: Spécifiez le nombre maximum d'itérations .
- normalize:Booléen.Si égal àTrue, Les données sont normalisées avant la formation au modèle . La normalisation présente deux avantages :
(1):Augmenter le taux de convergence du modèle, Réduire le temps de recherche de la solution optimale .
(2) Améliorer la précision du modèle . - copy_X:Booléen.Si défini àTrue, Une copie des données de formation sera copiée .
- precompute: Une valeur booléenne ou une séquence . Il détermine si le calcul est effectué à l'avance Gram Matrice pour accélérer le calcul .
- tol:Seuil. Déterminer si l'itération converge ou satisfait aux exigences de précision .
- warm_start:Booléen.Si ouiTrue, Alors Continuez avec les résultats de votre entraînement précédent . Sinon, commencez l'entraînement dès le début .
- positive:Booléen.Si ouiTrue, Ensuite, les composantes du vecteur de poids doivent être positives. .
- selection:String,C'est possible."cyclic"Ou"random". Il spécifie que chaque itération , Où choisir le vecteur de poids Composants à mettre à jour .
(1)“random”:Mise à jour, Sélectionnez au hasard une composante du vecteur de poids à mettre à jour .
(2)“cyclic”:Mise à jour, Sélectionnez un composant du vecteur de poids de l'avant à l'arrière pour mettre à jour . - random_state: Un entier ou un RandomStateExemple,OuNone.
(1):Si c'est un entier, Il spécifie la graine du générateur de nombres aléatoires .
(2):Si ouiRandomStateExemple, Il spécifie le générateur de nombres aléatoires .
(3):Si ouiNone, Le générateur de nombres aléatoires par défaut est utilisé .
Propriétés:
- coef_:Vecteur de poids.
- intercept_:InterceptionbValeur.
- 3.n_iter_:Nombre réel d'Itérations.
Méthodes:
- fit(X,y):Modèle d'entraînement.
- predict(X):Prévision à l'aide d'un modèle,Retour à la prévision.
- score(X,y): Renvoie le score du rendement prévu .
La formule de calcul est:: s c o r e = ( 1 − u / v ) score=(1 - u/v) score=(1−u/v)
Parmi eux u = ( ( y t r u e − y p r e d ) ∗ ∗ 2 ) . s u m ( ) , v = ( ( y t r u e − y t r u e . m e a n ( ) ) ∗ ∗ 2 ) . s u m ( ) u=((y_true - y_pred) ** 2).sum(),v=((y_true - y_true.mean()) ** 2).sum() u=((ytrue−ypred)∗∗2).sum(),v=((ytrue−ytrue.mean())∗∗2).sum()
scoreLa valeur maximale est1, Mais ça pourrait être négatif ( Les prévisions sont trop mauvaises ).scorePlus grand., Meilleure performance prédictive .
Régression logique-sklearnMéthode d'appel de la bibliothèque et explication des paramètres
from sklearn.linear_model import LogisticRegression
LogisticRegression(penalty=‘l2’,dual=False,tol=1e-4,C=1.0,
fit_intercept=True,intercept_scaling=1,class_weight=None,
random_state=None,solver=‘liblinear’,max_iter=100,
multi_class=‘ovr’,verbose=0,warm_start=False,n_jobs=1)
Signification des paramètres:
- penalty:String, Politique de régularisation spécifiée .Par défaut"l2"
(1)Si oui"l2", La fonction objective optimisée est : 0.5 ∗ ∣ ∣ w ∣ ∣ 2 2 + C ∗ L ( w ) , C > 0 0.5*||w||^2_2+C*L(w),C>0 0.5∗∣∣w∣∣22+C∗L(w),C>0, L(w) Pour la fonction de probabilité maximale .
(2)Si oui"l1", La fonction objective optimisée est ∣ ∣ w ∣ ∣ 1 + C ∗ L ( w ) , C > 0 ||w||_1+C*L(w),C>0 ∣∣w∣∣1+C∗L(w),C>0, L(w) Pour la fonction de probabilité maximale . - dual:Booléen.Par défautFalse.Si égal àTrue, Pour résoudre sa double forme .
Seulement sipenalty="l2"Etsolver="liblinear" Il n'y a qu'une double forme .Si ouiFalse, Résoudre la forme originale .Quandn_samples > n_features,Préférence pourdual=False. - tol:Seuil. Déterminer si l'itération converge ou satisfait aux exigences de précision .
- C:float,Par défaut1.0. Indique l'inverse du coefficient du terme de régularisation . Doit être un nombre flottant positif .CPlus la valeur est faible,Plus le terme de régularisation est grand.
- fit_intercept:boolValeur.Par défautTrue.Si ouiFalse,Je n'aurais pas calculébValeur.
- intercept_scaling:float, default 1.Seulement sisolver="liblinear"Et fit_intercept=TrueHeure,C'est logique.Dans ce cas,, Cela équivaut à ajouter une caractéristique à la dernière colonne des données de formation , Cette caractéristique est constante à 1. Son poids correspondant est b.
- class_weight:dict or ‘balanced’, default: None.
(1)Si c'est un dictionnaire, Donne le poids de chaque classification .Selon{class_label: weight}Cette forme.
(2)Si oui"balanced": Le poids de chaque classification est inversement proportionnel à la fréquence à laquelle la classification apparaît dans l'ensemble d'échantillons. .
n s a m p l e s / ( n c l a s s e s ∗ n p . b i n c o u n t ( y ) ) n_samples / (n_classes * np.bincount(y)) nsamples/(nclasses∗np.bincount(y))
(3)Si non spécifié, Le poids de chaque catégorie est 1. - random_state: int, RandomState instance or None, default: None
(1):Si c'est un entier, Il spécifie la graine du générateur de nombres aléatoires .
(2):Si ouiRandomStateExemple, Il spécifie le générateur de nombres aléatoires .
(3):Si ouiNone, Le générateur de nombres aléatoires par défaut est utilisé . - solver: String, Spécifier un algorithme pour résoudre le problème d'optimisation .
{‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’},default: ‘liblinear’
(1)solver=‘liblinear’,Pour les petits ensembles de données,'liblinear’C'est un bon choix.Pour les grands ensembles de données,‘sag’Et’saga’ Plus rapide à gérer .
(2)solver=‘newton-cg’, En utilisant la méthode newtonienne
(3)solver=‘lbfgs’,AdoptionL-BFGSMéthode quasi newtonienne.
(4)solver=‘sag’,AdoptionStochastic Average Gradient descentAlgorithmes.
(5)Pour les problèmes Multi - catégories,Seulement’newton-cg’,‘sag’,'saga’Et’lbfgs’ Gérer plusieurs pertes ;
‘liblinear’Limité à’ovr’Programme.
(6)newton-cg’, ‘lbfgs’ and ‘sag’ Ne peut traiter que L2 penalty,‘liblinear’ and ‘saga’ Ça marche. L1 penalty. - max_iter: Spécifiez le nombre maximum d'itérations .default: 100.C'est vrai.’newton-cg’, ‘sag’ and 'lbfgs’Application.
- multi_class:{‘ovr’, ‘multinomial’}, default: ‘ovr’. Préciser les politiques relatives aux questions de classification .
(1)multi_class=‘ovr’,Adoption’one_vs_rest’Stratégie.
(2)multi_class=‘multinomal’, Adopter directement la stratégie de régression logique Multi - catégories . - verbose: Utilisé pour activer ou désactiver la fonction de journalisation de sortie intermédiaire itérative .
- warm_start: Booléen.Si ouiTrue, Alors Continuez avec les résultats de votre entraînement précédent . Sinon, commencez l'entraînement dès le début .
- n_jobs: int, default: 1. Spécifie quand la tâche est parallèle CPUNombre.Si oui-1, Utilisez tous les CPU.
Propriétés:
- coef_:Vecteur de poids.
- intercept_:InterceptionbValeur.
- n_iter_:Nombre réel d'Itérations.
Méthodes:
- fit(X,y): Modèle d'entraînement.
- predict(X): Prédiction à l'aide d'un modèle bien formé, Et renvoie la valeur prévue .
- predict_log_proba(X): Renvoie un tableau,Les éléments du tableau sont à leur tourX Prédit en tant que paire de probabilités pour chaque catégorie .
- predict_proba(X): Renvoie un tableau,Les éléments du tableau sont à leur tourX Prédit comme valeur de probabilité pour chaque catégorie .
- score(X,y): Renvoie l'exactitude des prévisions.
Cas concrets:
Régression linéaire multiple
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn import datasets,linear_model,model_selection
from sklearn.model_selection import train_test_split
def load_data():
diabetes = datasets.load_diabetes()
return train_test_split(diabetes.data,diabetes.target,test_size=0.2)
def test_LineearRegression(*data):
X_train,X_test,y_train,y_test = data
regr = linear_model.LinearRegression()
regr.fit(X_train,y_train)
print('Coefficients:{},intercept:{}'.format(regr.coef_,regr.intercept_))
print('Residual sum of squares:{}'.format(np.mean(regr.predict(X_test)-y_test)**2))
print('Scores:{}'.format(regr.score(X_test,y_test)))
if __name__ == '__main__':
X_train,X_test,y_train,y_test = load_data()
test_LineearRegression(X_train,X_test,y_train,y_test)
LassoRetour
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets,linear_model
from sklearn.model_selection import train_test_split
def load_data():
diabetes = datasets.load_diabetes()
return train_test_split(diabetes.data,diabetes.target,test_size=0.2)
def test_Lasso(*data):
X_train,X_test,y_train,y_test = data
regr = linear_model.Lasso()
regr.fit(X_train,y_train)
print('Coefficients:{},intercept:{}'.format(regr.coef_,regr.intercept_))
print('Residual sum of squares:{}'.format(np.mean(regr.predict(X_test)-y_test)**2))
print('Scores:{}'.format(regr.score(X_test,y_test)))
def test_Lasso_alpha(*data):
X_train,X_test,y_train,y_test = data
alphas = [0.01,0.02,0.05,0.1,0.2,0.5,1,2,5,10,20,50,100,200,500,1000]
scores = []
for i,alpha in enumerate(alphas):
regr = linear_model.Lasso(alpha=alpha)
regr.fit(X_train,y_train)
scores.append(regr.score(X_test,y_test))
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(alphas,scores)
ax.set_xlabel("alpha")
ax.set_ylabel("score")
ax.set_xscale("log")
ax.set_title('Lasso')
plt.show()
if __name__ == '__main__':
X_train,X_test,y_train,y_test = load_data()
test_Lasso(X_train,X_test,y_train,y_test)
test_Lasso_alpha(X_train,X_test,y_train,y_test)
Retour en montagne(Ridge)
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets,linear_model
from sklearn.model_selection import train_test_split
def load_data():
diabetes = datasets.load_diabetes()
return train_test_split(diabetes.data,diabetes.target,test_size=0.2,random_state=0)
def test_Ridge(*data):
X_train,X_test,y_train,y_test = data
regr = linear_model.Ridge()
regr.fit(X_train,y_train)
print('Coefficients:{},intercept:{}'.format(regr.coef_,regr.intercept_))
print('Residual sum of squares:{}'.format(np.mean(regr.predict(X_test)-y_test)**2))
print('Scores:{}'.format(regr.score(X_test,y_test)))
def test_Ridge_alpha(*data):
X_train,X_test,y_train,y_test = data
alphas = [0.01,0.02,0.05,0.1,0.2,0.5,1,2,5,10,20,50,100,200,500,1000]
scores = []
for i,alpha in enumerate(alphas):
regr = linear_model.Lasso(alpha=alpha)
regr.fit(X_train,y_train)
scores.append(regr.score(X_test,y_test))
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(alphas,scores)
ax.set_xlabel("alpha")
ax.set_ylabel("score")
ax.set_xscale("log")
ax.set_title('Ridge')
plt.show()
if __name__ == '__main__':
X_train,X_test,y_train,y_test = load_data()
test_Ridge(X_train,X_test,y_train,y_test)
test_Ridge_alpha(X_train,X_test,y_train,y_test)
Régression logique
from math import exp
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data,columns=iris.feature_names)
df['label'] = iris.target
df.columns =['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
data = np.array(df.iloc[:100,[0,1,-1]])
return data[:,:2],data[:,-1]
X,y = create_data()
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
class LogisticRegressionClassifier(): #Mode personnalisé
def __init__(self,max_iter=700,learning_rate=0.01):
self.max_iter = max_iter
self.learning_rate = learning_rate
def sigmoid(self,x):
return x / (1+exp(-1))
def data_matrix(self,X):
data_mat = []
for d in X:
data_mat.append([1.0,*d])
return data_mat
def fit(self, X, y):
data_mat = self.data_matrix(X)
self.weights = np.zeros((len(data_mat[0]), 1), dtype=np.float32)
for iter_ in range(self.max_iter):
for i in range(len(X)):
result = self.sigmoid(np.dot(data_mat[i], self.weights))
error = y[i] - result
self.weights += self.learning_rate * error * np.transpose([data_mat[i]])
print('LogisticRegression Model(learning_rate={}, max_iter={})'.
format(self.learning_rate, self.max_iter))
def score(self, X_test, y_test):
right = 0
X_test = self.data_matrix(X_test)
for x, y in zip(X_test, y_test):
result = np.dot(x, self.weights)
if (result > 0 and y == 1) or (result < 0 and y == 0):
right += 1
return right / len(X_test)
lr_clf = LogisticRegressionClassifier()
lr_clf.fit(X_train, y_train)
lr_clf.score(X_test, y_test)
x_points = np.arange(4, 8)
y_ = -(lr_clf.weights[1] * x_points + lr_clf.weights[0]) / lr_clf.weights[2]
plt.plot(x_points, y_)
plt.scatter(X[:50, 0], X[:50, 1], label='0')
plt.scatter(X[50:, 0], X[50:, 1], label='1')
plt.legend()
#Mode d'appel
Logitic_model = linear_model.LogisticRegression()
Logitic_model.fit(X_train,y_train)
Logitic_model.score(X_test,y_test)
边栏推荐
猜你喜欢

Vert. x: A simple login access demo (simple use of router)
![[CDH] cdh5.16 configuring the setting of yarn task centralized allocation does not take effect](/img/e7/a0d4fc58429a0fd8c447891c848024.png)
[CDH] cdh5.16 configuring the setting of yarn task centralized allocation does not take effect
![[yarn] CDP cluster yarn configuration capacity scheduler batch allocation](/img/85/0121478f8fc427d1200c5f060d5255.png)
[yarn] CDP cluster yarn configuration capacity scheduler batch allocation

{一周总结}带你走进js知识的海洋
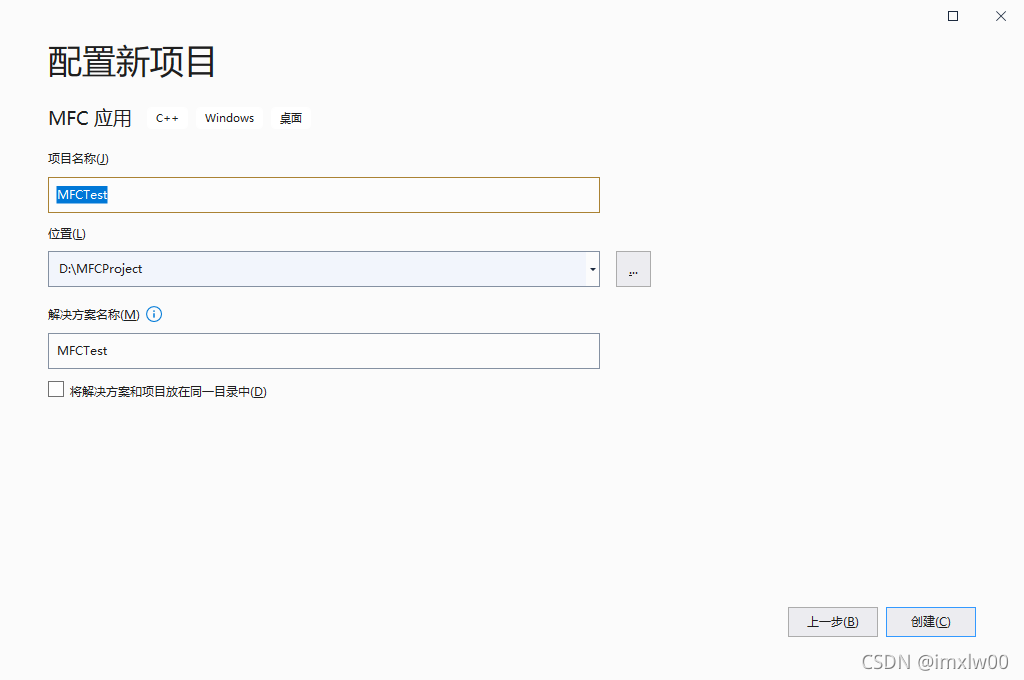
Vs2019 use wizard to generate an MFC Application
Valentine's Day flirting with girls to force a small way, one can learn
Double to int precision loss
Reading BMP file with C language

Linux Yum install MySQL
Vert. x: A simple TCP client and server demo
随机推荐
牛客Novice月赛40
分布式節點免密登錄
jS数组+数组方法重构
vs2019 使用向导生成一个MFC应用程序
L2-007 家庭房产 (25 分)
Learn winpwn (2) -- GS protection from scratch
第4阶段 Mysql数据库
Heating data in data lake?
Aborted connection 1055898 to db:
yarn安装与使用
C语言读取BMP文件
Principle and implementation of MySQL master-slave replication
{一周总结}带你走进js知识的海洋
Distribute wxWidgets application
MySQL and C language connection (vs2019 version)
分布式节点免密登录
Password free login of distributed nodes
ES6 promise object
Codeforces Round #753 (Div. 3)
互联网协议详解