B tree and b+ tree of MySQL index implementation

B Trees

Definition

B Trees are also called B- Trees , It is a multi-path balanced lookup tree , Generally describe a tree B You need to specify its order tree when you create a tree , The order indicates how many child nodes a node can have at most , In general, letters are used m Represents the order , When m take 2 when , It's our common binary search tree
commonly m Step B The tree is defined as follows ：

• Each node has at most m-1 Key words
• The root node can have at least one keyword
• Non root nodes have at least Math.ceil(m/2)-1 Key words
  TIP：Math.ceil() Express plus 0.5 Round down again
• The keywords in each node are arranged from the smallest to the largest , All keywords in the left subtree of each keyword are smaller than it , All keywords of the right subtree are larger than it
• All leaf nodes are located on the same layer , Or the length from the root node to each leaf node is the same

for example ：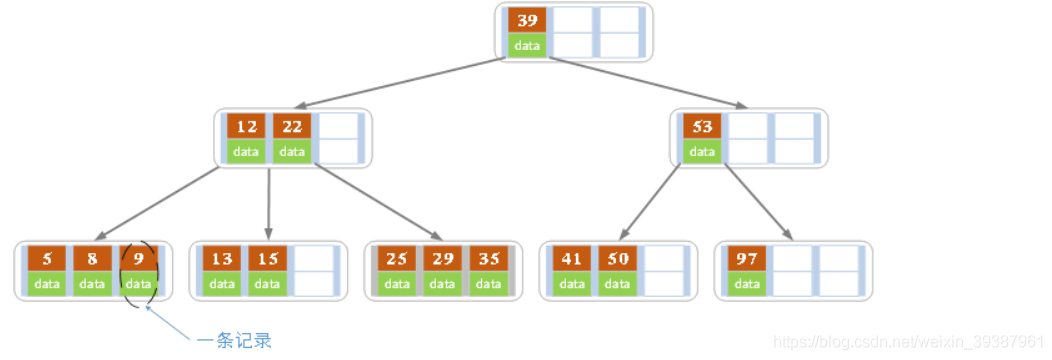

The figure above shows a star with order 4 Of B Trees . In practical application B The order of the tree m They are very big （ Usually greater than 100）, So even if you store a lot of data ,B The height of the tree is still small . Keywords are stored in each node （key） Data corresponding to keywords （data）, And the pointer to the child node . We will key Corresponding to it data It's called a record . But for ease of description , Unless otherwise specified , In the following article, we will use key Instead of （key, value） The key value pairs the whole . In the database, we will B Trees （ and B+ Trees ） As an index structure , Can speed up the query speed , here B In the tree key It means key , and data Indicates the logical address of the entry corresponding to this key on the hard disk .

B Tree insert operation

The insert operation inserts a record , namely （key,value） The key/value pair . If B The key value pair to be inserted already exists in the tree , Use the... To be inserted value Replace old value, if B Tree species do not exist key, Then the insertion operation must be carried out in the leaf node

• According to the key value , Find the leaf node and insert
• Judge the current node key Whether the number of is less than or equal to m-1, If satisfied, end , Otherwise proceed to the next step
• In the middle of the node key Split into left and right parts , Then put this in the middle key Insert into parent node , This key The left subtree of points to the left half of the split , This key The right subtree of points to the right half of the split , Then point the current node to the parent node , Continue with this step

for example ：
With 5 rank B Trees, for example , Introduce B Tree insert operation , stay 5 rank B In the tree , There are at most 4 individual key, At least 2 individual key

1. Insert... In an empty tree 39
   
   The root node has 4 individual key
2. Continue to insert 22,97 and 41
   
   The root node has 4 individual key
3. Continue to insert 53
   
   The maximum number of keywords allowed after insertion has been exceeded 4, So key The value is 41 Split at the center , give the result as follows , After splitting, the current node pointer points to the parent node , Satisfy B Tree condition , End of insertion . Contemporary tree m For even when , When you need to split, there is no one in the middle key, Then you can choose the previous one in the middle key Or the last one in the middle key Just split the center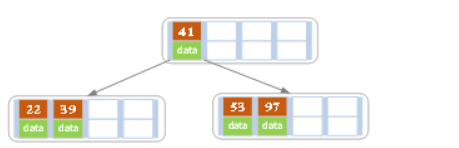
   
4. Insert... In turn 13,21,40, It will also cause division
   
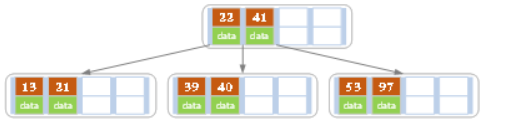
5. Insert... In turn 30,27, 33 ;36,35,34 ;24,29
   
6. Insert key The value is 26 The record of
   
7. The current node needs to be marked with 27 Split at the center , And carry to the parent node 27, Then the current node points to the parent node
   
8. Carry will cause the current node （ The root node ） It also needs to be divided
   
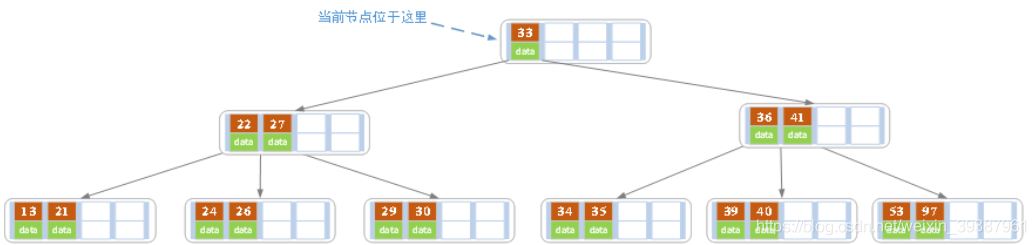
   After splitting, the current node points to the new root , There is no need to adjust .
9. Finally, insert key by 17,28,29,31,32 The record of
   

In the realization of B In the code of the tree , To make coding easier , We can define the length of the array of records stored in the node as m Instead of m-1, This is convenient for the bottom node to insert a record into the upper layer due to splitting , The upper layer has extra space to store this record . meanwhile , Each node can also store a reference to its parent node , In this way, there is no need to write recursive programs .
Generally speaking , For certain m And determine the type of records , The node size is fixed , No matter how many records it actually stores , But the method of allocating fixed node size will be wasteful , such as key by 28,29 The node , also 2 individual Key The location of is not used , But it is no longer possible to insert any values , Because the preamble of this node key yes 27, follow-up key yes 30, All integer values are used up , So if you record, press key Size in order , Insert again B In the tree , The utilization rate of nodes will be very low , In the worst case, the utilization rate is only 50%.

B Tree deletion

Delete means , according to Key Delete record , If B There is no corresponding record in the tree key The record of , Delete failed

• If you need to delete key On non leaf nodes , Follow up key（ This refers to the follow-up key Both mean follow-up records ） Overwrite the key, Then in the follow-up key Delete the subsequent key, Now follow up key It must be on the leaf node , This process is similar to deleting nodes in a binary search tree , Delete this record and proceed to the next step
• The node key The number is greater than or equal to Math.ceil(m/2)-1, End deletion , Otherwise go to the next step
• If brother node key The number is greater than Math.ceil(m/2)-1, Then key Move down to this node , One of the sibling nodes Key Move upward , End of delete operation

otherwise , Set key Move down with the current node and its sibling nodes key Merge , Form a new node , In the original parent node key Two children's hands become one child's hands , Point to this new node , Then the current node pointer points to the parent node , Repeat the second step of judgment
Some nodes may have both left brothers , Another right brother , Then we can choose any brother node to operate

for example ：
With 5 rank B Trees, for example , Introduce B Tree deletion ,5 rank B In the tree , There are at most 4 individual key, At least 2 individual key

1. Original state
   
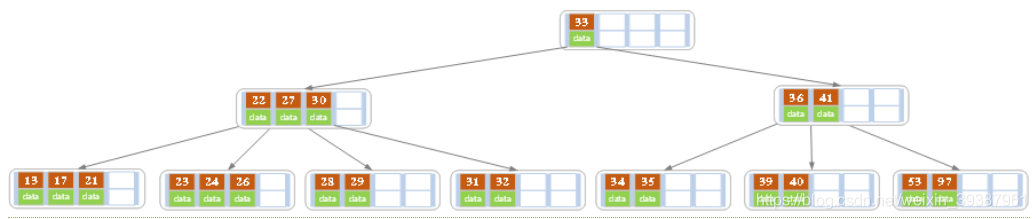
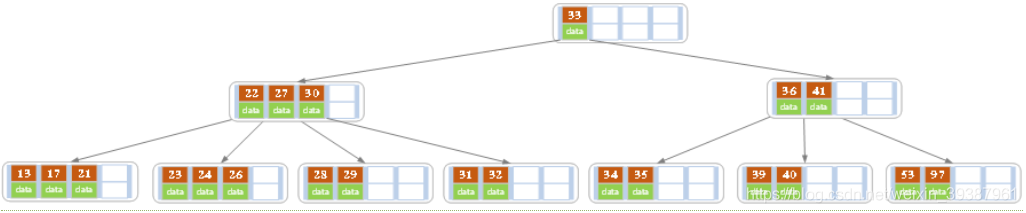
2. Above B Delete... From the tree 21, After deletion, the number of keywords in the node is still greater than equal 2, So the deletion ends
   
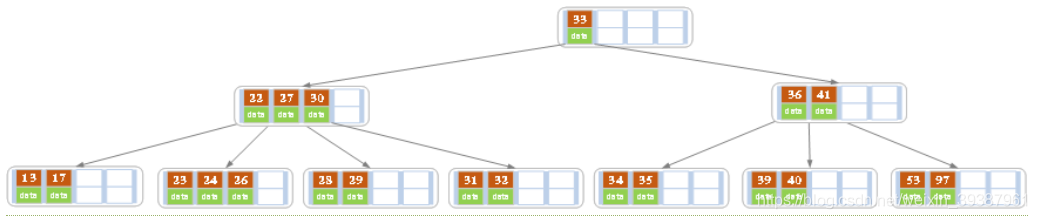
3. In the above case, delete 27. It can be seen from the figure above 27 Located in non leaf nodes , So use 27 And replace it . As you can see from the diagram ,27 Subsequent to 28, We use it 28 Replace 27, And then in 28（ primary 27） Delete from the right child node of 28. The deleted result is shown in the following figure
   
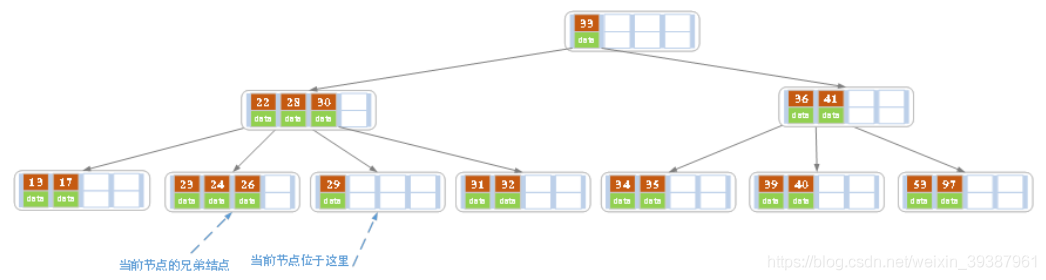
   Found after deletion , The number of records of the current leaf node is less than 2, Among its sibling nodes 3 A record （ The current node also has a right brother , Selecting the right brother will lead to the merging of nodes , Whichever one you choose will do , It's just the end B The shape of the tree will be different ）, At this time, intercept one from the brother node key, So in the parent node 28 Move down , Brothers, but 26 Move upward , Delete end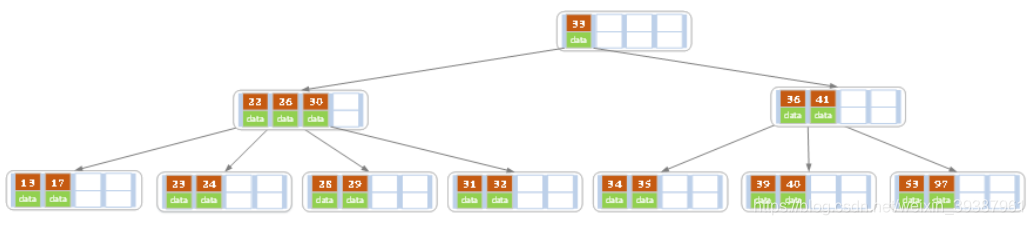
   
4. In the above case, then 32
   
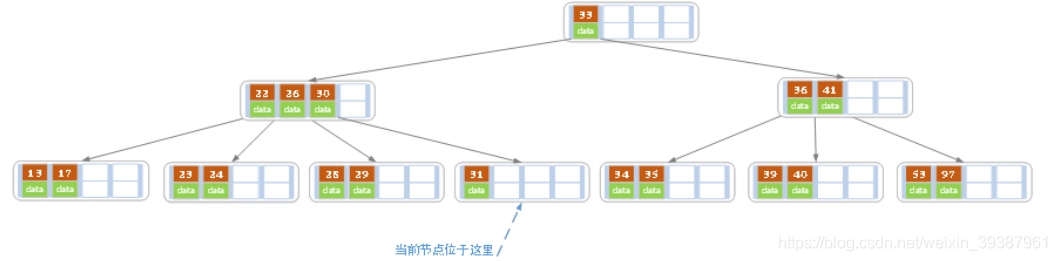
   When deleted , There are only key, And brother nodes are only 2 individual key, So only the parent node 30 Move down and... In this two child node key Merge , Become a new node , The current node points to the parent node
   The current node key The number of meets the condition , So the deletion ends
5. In the above case , We then delete key by 40 The record of
   
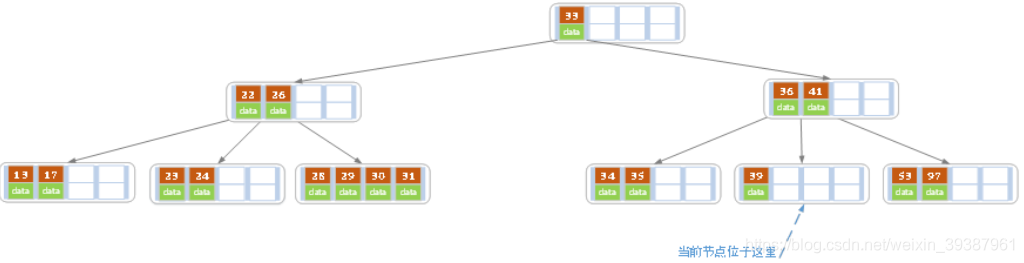
   Empathy , The number of records in the current node is less than 2, There is no redundancy in brother nodes key, So in the parent node key Move down , And brothers （ Here we choose left brother , You can also choose the right brother ） Node merging , The merged pointer to the current node points to the parent node
   Empathy , For the current node, you can only continue to merge
   
   After merging, the current node meets the conditions , Delete end

B+ Trees

Definition

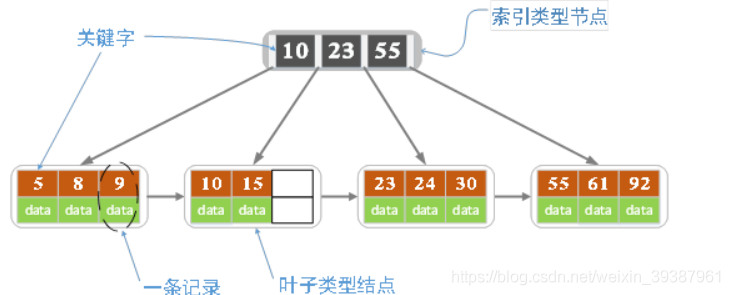
Keywords are smaller than child nodes 1, The figure above shows a star with order 4 Of B+ Trees

• B+ The tree contains two types of systems, but ： Internal node （ The index node ） And leaf nodes , The root node itself can be either an internal node , It can also be a leaf node , The minimum number of keywords in the root node can be 1 individual .
• B+ Trees and B The biggest difference of the tree is that the internal nodes do not save data , Index only , All the data （ The latter says record ） Are saved in leaf nodes
• m rank B+ The tree indicates that there are at most m-1 Key words （ Or the maximum number of internal nodes is m Subtree ）, Step tree m At the same time, it limits the maximum storage capacity of leaf nodes m-1 A record
• In the internal node key All in order from small to large , For one of the internal nodes key, All in the left tree key All smaller than it , In the right subtree key Are greater than or equal to it . The records in the leaf node are also recorded according to key The size of
• Each leaf node has a pointer to an adjacent leaf node , Leaf nodes themselves are linked from small to large according to the size of keywords

B+ Tree insert operation

• If it's an empty tree , Create a leaf node , Then insert the record into it , At this time, this leaf is also the root node , End of insertion
• For leaf type nodes : according to key Value to find the leaf node , Insert a record into this leaf , After inserting , If the current node key The number of is less than or equal to m-1, Then insert the end . Otherwise, split the leaf node into left and right leaf nodes , The left leaf node contains the front m/2 A record , The right node contains the remaining records , Will be the first m/2+1 A recorded key Carry into the parent node （ The parent node must be an index type node ）, Carry to parent node key Left child pointer left node , The right child pointer points to the right node . Point the pointer of the current node to the parent node , Then go to the next step
• For index type nodes ： If the current node key The number of is less than or equal to m-1, Then insert the end . otherwise , Split this index type node into two index nodes , The left inode contains （m-1）/2 individual Key, The right node contains m-(m-1)/2 individual key, Will be the first m/2 individual key Carry into the parent node , Carry to parent node key The left child of points to the left node , Carry to parent node key The right child of points to the right node . Point the pointer of the current node to the parent node , Then repeat this step

for example ：
Here is a 5 rank B Tree insertion process ,5 rank B The number of nodes is the least 2 individual key, most 4 individual key

1. Insert in empty tree 5
   
2. Insert... In turn 8,10,15
   
3. Insert 16
   
   Insert 16 After the number of keywords exceeded the limit , So split up . When leaf nodes split , Split left node 2 A record , On the right 3 A record , middle key Become... In the inode key, After separation, the current node points to the parent node （ The root node ）. as follows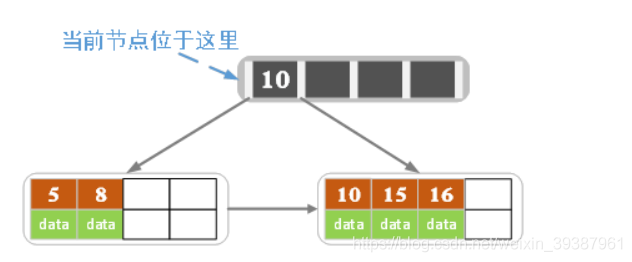
   
   Of course, it can also be another way of division , To the left node 3 A record , Right node 2 A record , At this time key It becomes 15
4. Insert 17
   
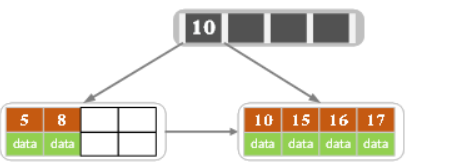
5. Insert 18
   
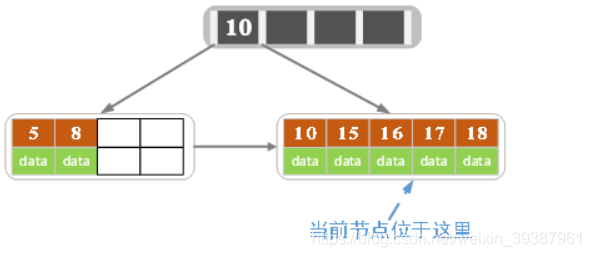
   The number of keywords in the current node is greater than 5, Split up , Split into two nodes , The left node 2 A record , Right node 3 A record , keyword 16 Carry to parent node （ The index node ） in , Point the pointer of the current node to the parent node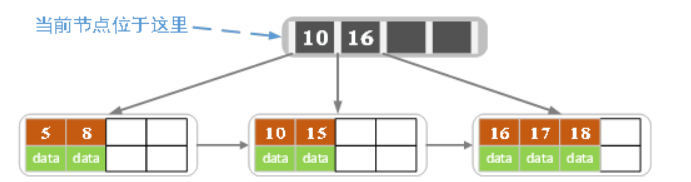
   
   The number of keywords of the current node meets the condition , Insert the end
6. After inserting some data
   
7. Insert... In the picture above 7
   
   The number of keywords in the current node exceeds 4, Need to split , The left node 2 A record , Right node 3 A record .
   Keywords after splitting 7 Enter the parent node , Point the pointer of the current node to the parent node , as follows
   
   The number of keywords in the current node exceeds 4, Need to continue to split , The left node 2 Key words , Right node 2 Key words , keyword 16 Enter the parent node , Point the current node to the parent node , as follows ：
   
   The number of keywords of the current node meets the condition , Insert the end

B+ Tree deletion

If there is no corresponding key, Delete failed , Otherwise, perform the following steps

• Delete the corresponding key, If the node is deleted key The number is greater than or equal to Math.ceil(m-1)/2-1, End of delete operation , Otherwise, go to the second step
• If brother node key There is a surplus （ Greater than Math.ceil(m-1)/2-1）, Borrow a record from a brother node , At the same time use the borrowed key Replace parent node （ It refers to the parent node shared by the current node and brother nodes ） Medium key, Delete end , Otherwise go to the next step
• If there is no surplus in the sibling node key, Then the current node and brother nodes are merged into a new leaf node , And delete key( This in the parent node key The children's hands on both sides become hands , Just point to this new leaf node ), Point the current node to the parent node （ Must be an inode ）, Perform the next step
• If the index node key The number of is greater than or equal to Math.ceil(m-1)/2-1, The deletion operation is finished , Otherwise go to the next step
• If brother nodes have surplus , Parent node key Move down , Brother node moves up , Delete end , Otherwise go to the next step
• Move the current node, sibling node and parent node down key Merge into a new node , Point the current node to the parent node , Repeat step four

Be careful , adopt B+ After deleting the tree , Exist in the inode key, There is not necessarily a corresponding record in the leaf node
for example ：
Here is a 5 rank B Tree deletion process ,5 rank B The number of nodes is the least 2 individual key, most 4 individual key

1. The initial state
   
2. Delete 22
   
   Delete the leaf node key The number of is greater than or equal to 2, Delete end
3. Delete 15
   
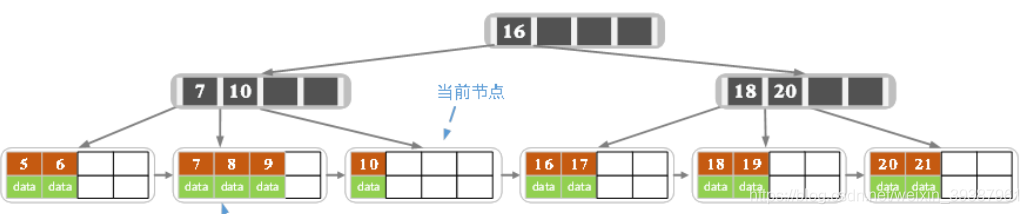
   After deletion, there is only one current node key, Not meeting the conditions , There are three sibling nodes key, You can borrow a keyword from the brother node as 9 The record of , At the same time, update the key in the parent node by 10 Turn into 9, Delete end
   
4. Delete 7
   
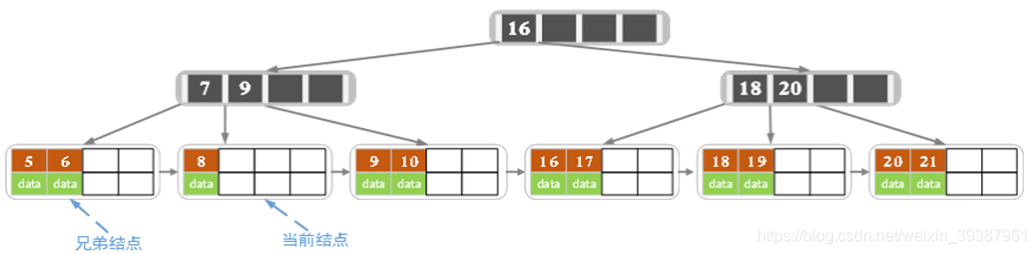
   The number of keywords in the current node is less than 2, There are no spare keywords in the left brother node （ The current node also has a brother , But any one can be split , We choose the one on the left ）, So the current node and the sibling node are merged , And delete key, The current node points to the parent node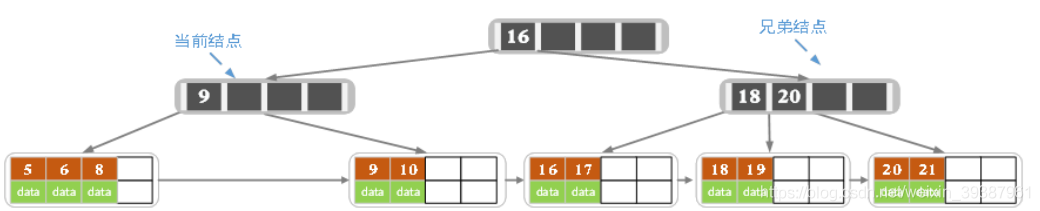
   
   At this time, the number of keywords in the current node is less than 2, There is no surplus of keywords in brother nodes , So the keyword in the parent node moves down , Merge with two child nodes , as follows
   

complete ~