当前位置:网站首页>Mysql的索引实现之B树和B+树
Mysql的索引实现之B树和B+树
2022-07-06 09:15:00 【乘风破BUG】
B树
定义
B树也称为B-树,它是一棵多路平衡查找树,一般描述一棵B树时需要指定它的阶树,阶数表示一个节点最多可以有多少个孩子节点,一般用字母m表示阶数,当m取2时,就是我们常见的二叉搜索树
一般m阶的B树定义如下:
- 每个节点最多有m-1个关键字
- 根节点最少可以只有一个关键字
- 非根节点至少有Math.ceil(m/2)-1个关键字
TIP:Math.ceil()表示加上0.5再向下取整 - 每个节点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树的所有关键字都大于它
- 所有叶子节点的都位于同一层,或者说根节点到每个叶子节点的长度都相同
例如: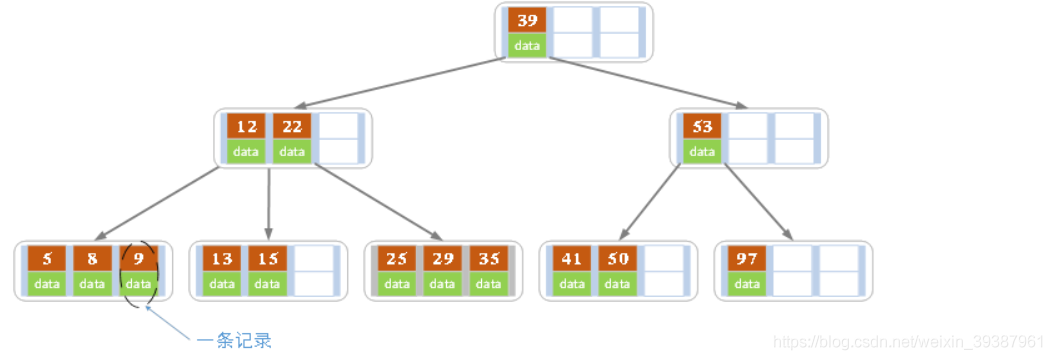
上图是一颗阶数为4的B树。在实际应用中的B树的阶数m都非常大(通常大于100),所以即使存储大量的数据,B树的高度仍然比较小。每个结点中存储了关键字(key)和关键字对应的数据(data),以及孩子结点的指针。我们将一个key和其对应的data称为一个记录。但为了方便描述,除非特别说明,后续文中就用key来代替(key, value)键值对这个整体。在数据库中我们将B树(和B+树)作为索引结构,可以加快查询速速,此时B树中的key就表示键,而data表示了这个键对应的条目在硬盘上的逻辑地址。
B树的插入操作
插入操作既插入一条记录,即(key,value)的键值对。如果B树中已经存在需要插入的键值对,则用需要插入的value替换旧的value,若B树种不存在这个key,则一定是在叶子节点中进行插入操作
- 根据要插入的key值,找到叶子节点并插入
- 判断当前节点key的个数是否小于等于m-1,若满足则结束,否则进行下一步
- 以节点中间的key为中心分裂成左右两部分,然后将这个中间的key插入到父节点中,这个key的左子树指向分裂后的左半部分,这个key的右子树指向分裂后的右半部分,然后将当前节点指向父节点,继续进行该步骤
例如:
以5阶B树为例,介绍B树的插入操作,在5阶B树中,结点最多有4个key,最少有2个key
- 在空树中插入39

根结点此时有4个key - 继续插入22,97和41

根结点此时有4个key - 继续插入53

插入后超过了最大允许的关键字个数4,所以以key值为41为中心进行分裂,结果如下,分裂后当前节点指针指向父节点,满足B树条件,插入操作结束。当阶树m为偶数时,需要分裂时就不存在排序恰好在中间的key,那么就可以选择中间位置的前一个key或者中间位置的后一个key为中心进行分裂即可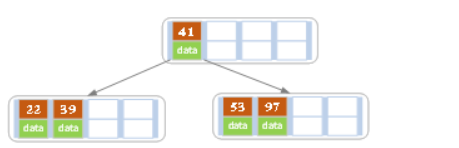
- 依次插入13,21,40,同样会造成分裂
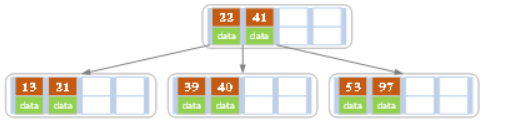
- 依次插入30,27, 33 ;36,35,34 ;24,29

- 插入key值为26的记录

- 当前结点需要以27为中心分裂,并向父结点进位27,然后当前结点指向父结点

- 进位后导致当前结点(即根结点)也需要分裂
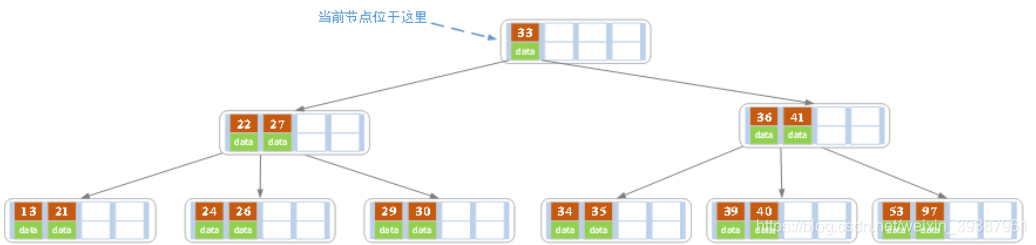
分裂后当前结点指向新的根,此时无需调整。 - 最后再依次插入key为17,28,29,31,32的记录
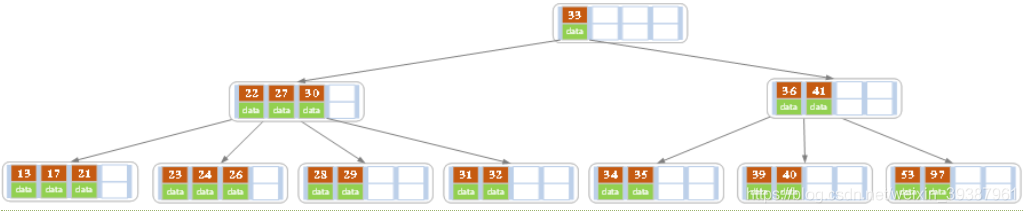
在实现B树的代码中,为了使代码编写更加容易,我们可以将节点中存储记录的数组长度定义为m而非m-1,这样方便底层的节点由于分裂向上层插入一个记录时,上层有多余的位置存储这个记录。同时,每个节点还可以存储它的父节点的引用,这样就不必编写递归程序。
一般来说,对于确定的m和确定类型的记录,节点大小是固定的,无论它实际存储了多少个记录,但是分配固定节点大小的方法会存在浪费的情况,比如key为28,29所在的节点,还有2个Key的位置没有使用,但是已经不可能再插入任何值了,因为这个节点的前序key是27,后续key是30,所有整数值都用完了,所以如果记录先按key大小排好序,再插入B树中,节点的使用率就会很低,最差情况下使用率仅为50%。
B树的删除操作
删除操作是指,根据Key删除记录,如果B树中的记录中不存在对应key的记录,则删除失败
- 如果当前需要删除的key位于非叶子节点上,则用后续key(这里指的后续key均指后续记录的意思)覆盖要删除的key,然后在后续key所在的子支中删除该后续key,此时后续key一定位于叶子节点上,这个过程和二叉搜索树删除节点的方式类似,删除这个记录后执行下一步
- 该节点key个数大于等于Math.ceil(m/2)-1,结束删除操作,否则执行下一步
- 如果兄弟节点key个数大于Math.ceil(m/2)-1,则父节点中的key下移到该节点,兄弟节点中一个Key上移,删除操作结束
否则,将父节点中的key下移与当前节点及它的兄弟节点中的key合并,形成一个新的节点,原父节点中的key的两个孩子指针就变成了一个孩子指针,指向这个新节点,然后当前节点指针指向父节点,重复判断第二步
有些节点它可能既有左兄弟,又有右兄弟,那么我们任意选择一个兄弟节点进行操作即可
例如:
以5阶B树为例,介绍B树的删除操作,5阶B树中,结点最多有4个key,最少有2个key
- 原始状态
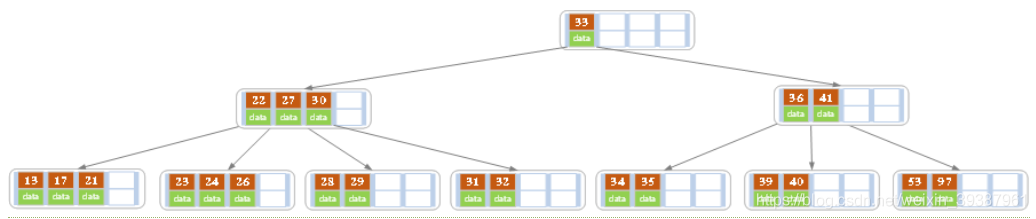
- 在上面的B树中删除21,删除后结点中的关键字个数仍然大于等2,所以删除结束
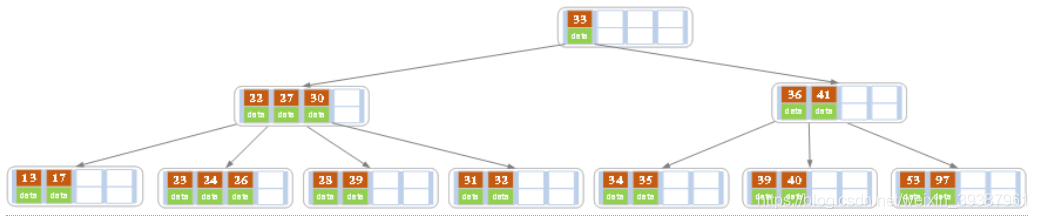
- 在上述情况下接着删除27。从上图可知27位于非叶子结点中,所以用27的后继替换它。从图中可以看出,27的后继为28,我们用28替换27,然后在28(原27)的右孩子结点中删除28。删除后的结果如下图所示
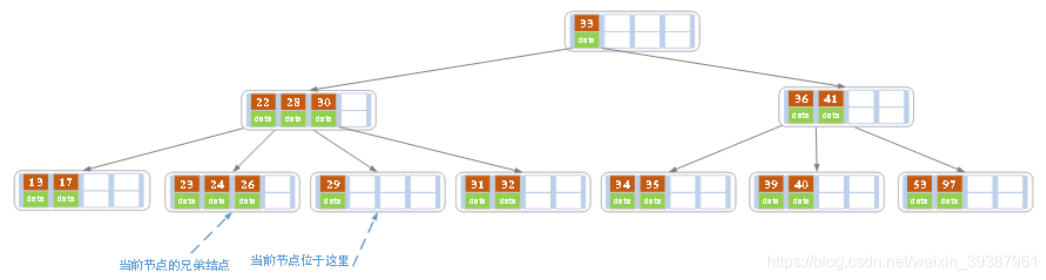
删除后发现,当前叶子节点的记录的个数小于2,而它的兄弟节点中有3个记录(当前节点还有一个右兄弟,选择右兄弟就会出现合并节点的情况,不论选择哪一个都行,只是最后B树的形态会不一样而已),此时从兄弟节点中截取一个key,所以父节点中28下移,兄弟系欸但的26上移,删除结束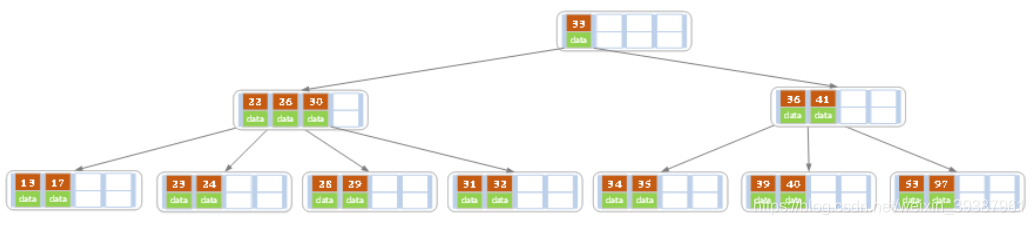
- 在上述情况下接着32
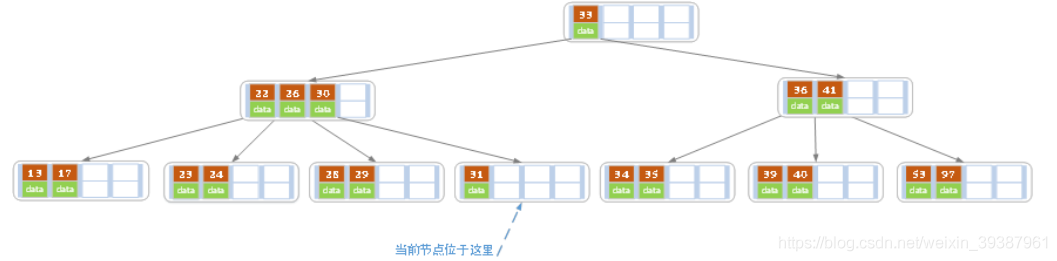
当删除后,当前节点中只有key,而兄弟节点也仅有2个key,所以只能让父节点的30下移和这个两个孩子节点中的key合并,成为一个新的节点,当前节点指向父节点
当前结点key的个数满足条件,故删除结束 - 上述情况下,我们接着删除key为40的记录
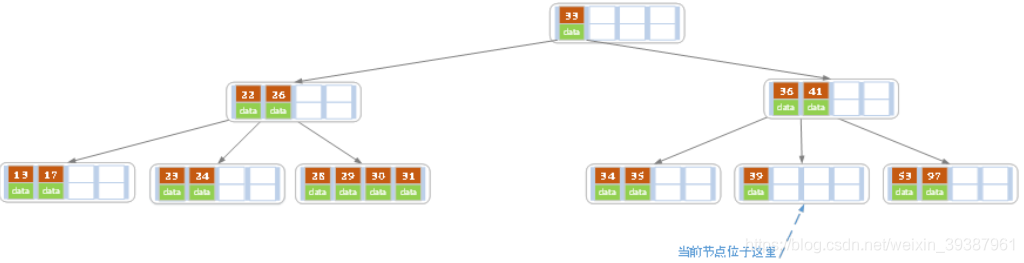
同理,当前节点的记录数小于2,兄弟节点中没有多余key,所以父节点中key下移,和兄弟(这里我们选择左兄弟,选择右兄弟也可以)节点合并,合并后的指向当前节点的指针就指向了父节点
同理,对于当前结点而言只能继续合并了
合并后结点当前结点满足条件,删除结束
B+树
定义
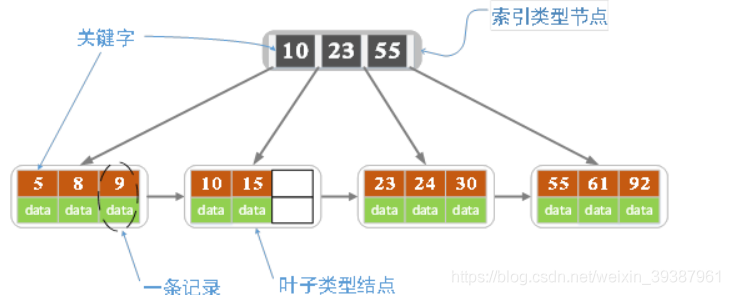
关键字比孩子节点小1,上图是一颗阶数为4的B+树
- B+树包含两种类型的系欸但:内部节点(索引节点)和叶子节点,根节点本身既可以是内部节点,也可以是叶子节点,根节点的关键字个数最少可以只有1个。
- B+树和B树最大的不同是内部节点不保存数据,只用于索引,所有数据(后者说记录)都保存在叶子节点中
- m阶B+树表示了内部节点最多有m-1个关键字(或者说内部节点最多有m个子树),阶树m同时限制了叶子节点最多存储m-1个记录
- 内部节点中key都按照从小到大的顺序排列,对于内部节点中的一个key,左树中的所有key都小于它,右子树中的key都大于等于它。叶子节点中的记录也按照key的大小排列
- 每个叶子节点都存有相邻叶子节点的指针,叶子节点本身依关键字的大小自小而大顺序链接
B+树的插入操作
- 若为空树,创建一个叶子节点,然后将记录插入其中,此时这个叶子也是根节点,插入操作结束
- 针对叶子类型节点:根据key值找到叶子节点,向这个叶子插入记录,插入后,若当前节点key的个数小于等于m-1,则插入结束。否则将这个叶子节点分裂成左右两个叶子节点,左叶子节点包含前m/2个记录,右节点包含剩下的记录,将第m/2+1个记录的key进位到父节点中(父节点一定是索引类型节点),进位到父节点的key左孩子指针向左节点,右孩子指针指向右节点。将当前节点的指针指向父节点,然后执行下一步
- 针对索引类型节点:若当前节点key的个数小于等于m-1,则插入结束。否则,将这个索引类型节点分裂成两个索引节点,左索引节点包含(m-1)/2个Key,右节点包含m-(m-1)/2个key,将第m/2个key进位到父节点中,进位到父节点的key的左孩子指向左节点,进位到父节点的key的右孩子指向右节点。将当前节点的指针指向父节点,然后重复这一步
例如:
下面是一颗5阶B树的插入过程,5阶B数的结点最少2个key,最多4个key
- 空树中插入5
- 依次插入8,10,15

- 插入16

插入16后超过了关键字的个数限制,所以要进行分裂。在叶子节点分裂时,分裂出来的左节点2个记录,右边3个记录,中间key成为索引节点中的key,分离后当前节点指向父节点(根节点)。如下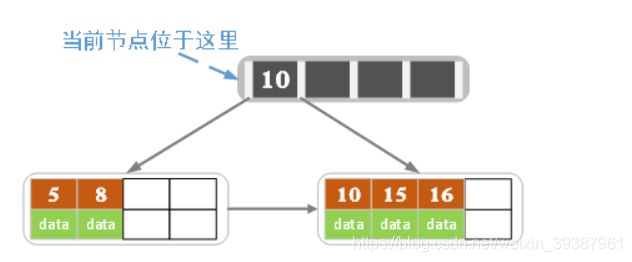
当然也可以是另一种分裂方式,给左节点3个记录,右节点2个记录,此时索引节点中的key就变成了15 - 插入17
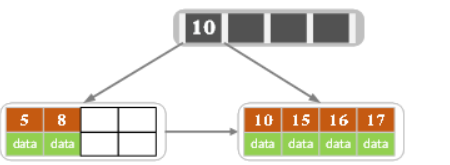
- 插入18
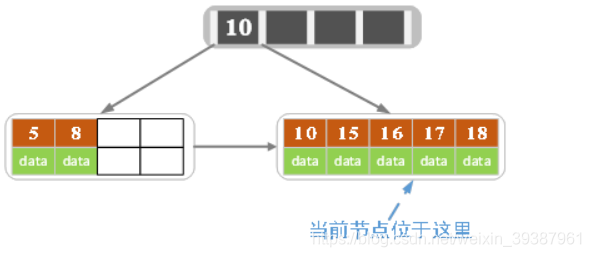
当前节点的关键字个数大于5,进行分裂,分裂成两个节点,左节点2个记录,右节点3个记录,关键字16进位到父节点(索引节点)中,将当前节点的指针指向父节点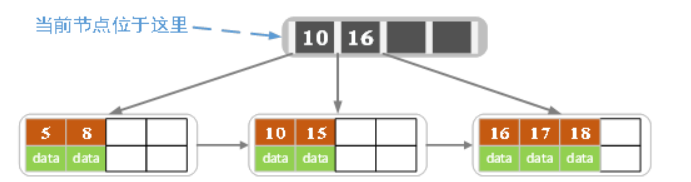
当前结点的关键字个数满足条件,插入结束 - 插入若干数据后

- 在上图中插入7

当前节点的关键字个数超过4,需要分裂,左节点2个记录,右节点3个记录。
分裂后关键字7进入到父节点中,将当前节点的指针指向父节点,如下
当前节点的关键字个数超过4,需要继续分裂,左节点2个关键字,右节点2个关键字,关键字16进入到父节点中,将当前节点指向父节点,如下:
当前结点的关键字个数满足条件,插入结束
B+树的删除操作
如果叶子节点中没有相应的key,则删除失败,否则执行下面步骤
- 删除叶子节点中对应的key,删除后若节点的key个数大于等于Math.ceil(m-1)/2-1,删除操作结束,否则执行第二步
- 若兄弟节点key有富余(大于Math.ceil(m-1)/2-1),向兄弟节点借一个记录,同时用借到的key替换父节点(指当前节点和兄弟节点共同的父节点)中的key,删除结束,否则执行下一步
- 若兄弟节点中没有富余的key,则当前节点和兄弟节点合并成一个新的叶子节点,并删除父节点中的key(父节点中的这个key两边的孩子指针就变成了一个指针,正好指向这个新的叶子节点),将当前节点指向父节点(必为索引节点),执行下一步
- 若索引节点的key的个数大于等于Math.ceil(m-1)/2-1,则删除操作结束,否则执行下一步
- 若兄弟节点有富余,父节点key下移,兄弟节点上移,删除结束,否则执行下一步
- 当前节点和兄弟节点及父节点下移key合并成一个新的节点,将当前节点指向父节点,重复第四步
注意,通过B+树的删除操作后,索引节点中存在的key,不一定在叶子节点中存在对应的记录
例如:
下面是一颗5阶B树的删除过程,5阶B数的结点最少2个key,最多4个key
- 初始状态

- 删除22

删除后叶子结点中key的个数大于等于2,删除结束 - 删除15
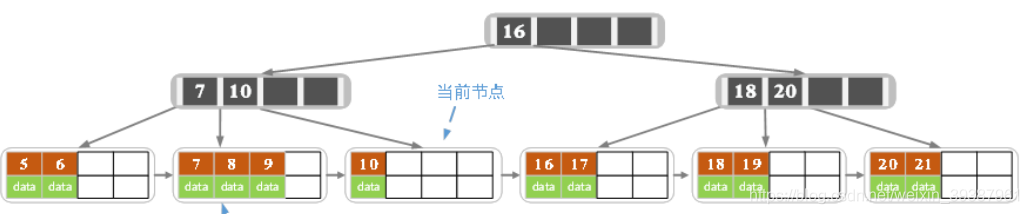
删除后当前节点只有一个key,不满足条件,而兄弟节点有三个key,可以从兄弟节点借一个关键字为9的记录,同时更新将父节点中的关键由10变为9,删除结束
- 删除7
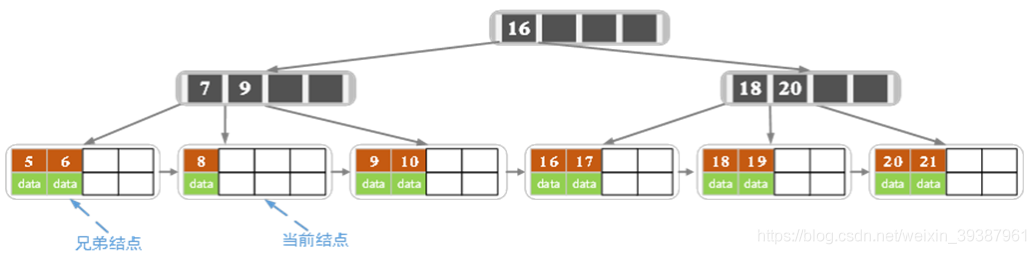
当前节点关键字个数小于2,左兄弟节点中也没有富余的关键字(当前节点还有个有兄弟,不过任意一个进行分拆就可以了,我们选择左边的),所以当前节点和兄弟节点合并,并删除父节点中的key,当前节点指向父节点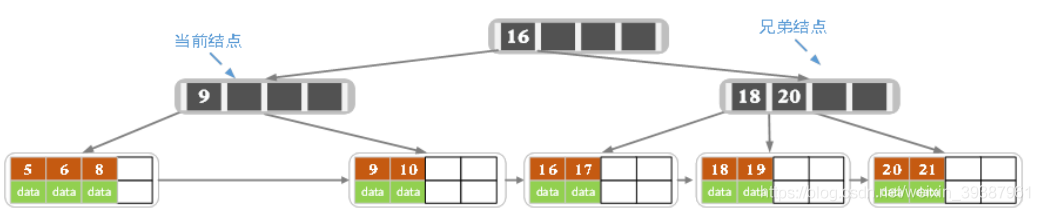
此时当前节点的关键字个数小于2,兄弟节点的关键字也没有富余,所以父节点中的关键字下移,和两个孩子节点合并,如下
完毕~
边栏推荐
- Word排版(小计)
- L2-004 这是二叉搜索树吗? (25 分)
- Nanny level problem setting tutorial
- Aborted connection 1055898 to db:
- Punctual atom stm32f103zet6 download serial port pin
- [蓝桥杯2021初赛] 砝码称重
- wangeditor富文本组件-复制可用
- Database advanced learning notes -- SQL statement
- 02 staff information management after the actual project
- 使用lambda在循环中传参时,参数总为同一个值
猜你喜欢
C语言读取BMP文件
AcWing 1298. Solution to Cao Chong's pig raising problem
vs2019 桌面程序快速入门
QT creator custom build process

PHP - whether the setting error displays -php xxx When PHP executes, there is no code exception prompt
![[number theory] divisor](/img/ec/036d7e76cc566c08d336444f2898e1.jpg)
[number theory] divisor
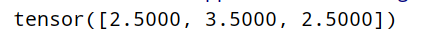
Pytoch Foundation
![[蓝桥杯2017初赛]方格分割](/img/e9/e49556d0867840148a60ff4906f78e.png)
[蓝桥杯2017初赛]方格分割

2019腾讯暑期实习生正式笔试
Valentine's Day flirting with girls to force a small way, one can learn
随机推荐
Request object and response object analysis
Julia 1.6 1.7 common problem solving
express框架详解
[MRCTF2020]套娃
[蓝桥杯2020初赛] 平面切分
[yarn] yarn container log cleaning
vs2019 桌面程序快速入门
yarn安装与使用
L2-004 is this a binary search tree? (25 points)
Deoldify project problem - omp:error 15:initializing libiomp5md dll,but found libiomp5md. dll already initialized.
Introduction to the easy copy module
QT creator test
Solution of deleting path variable by mistake
Reading BMP file with C language
Heating data in data lake?
搞笑漫画:程序员的逻辑
数据库高级学习笔记--SQL语句
double转int精度丢失问题
[download app for free]ineukernel OCR image data recognition and acquisition principle and product application
L2-007 家庭房产 (25 分)