当前位置:网站首页>[蓝桥杯2021初赛] 砝码称重
[蓝桥杯2021初赛] 砝码称重
2022-07-06 09:14:00 【%xiao Q】
题目
题目描述
你有一架天平和N 个砝码,这N 个砝码重量依次是W1, W2, … , WN。
请你计算一共可以称出多少种不同的重量?
注意砝码可以放在天平两边。
输入格式
输入的第一行包含一个整数N。
第二行包含N 个整数:W1, W2, W3, … , WN。
对于50% 的评测用例,1 ≤ N ≤ 15。
对于所有评测用例,1 ≤ N ≤ 100,N 个砝码总重不超过100000。
输出格式
输出一个整数代表答案。
输入样例
3
1 4 6
输出样例
10
分析
这道题暴力搜索肯定是会超时的,dfs大概的话,能过50%的点。
这题的正解为dp(奈何菜鸡不会dp),那么接下来就来分析dp的做法:
- 状态表示f[i][j]:表示前i个砝码中选,称出的重量为j的状态,为1表示可以称出,为0则不能称出。
- 状态转移:
- a[i] == j,那么f[i][j]一定可以被称出
- a[i] != j,那么就可以从f[i - 1][j],f[i - 1][abs(j - a[i])](本质为f[i - 1][j - a[i]],为了防止出现负的下标,所以取绝对值),f[i - 1][j + a[i]]这3种情况中转移过来。
f[i - 1][j]:i - 1个砝码能称出的,i个也能称出
f[i - 1][j - a[i]]:加上当前的砝码
f[i - 1][j + a[i]]:减去当前的砝码
满足3种的任意一种,即可判断f[i][j]的重量为j的能否被称出
参考代码1(dfs)---- 过50%的样例(O(3^n))
#include <iostream>
#include <cstdio>
#include <set>
#include <map>
#include <vector>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <algorithm>
#include <unordered_map>
#define LL long long
#define rep(i, a, b) for(int i = a; i <= b; i++)
#define reps(i, a, b) for(int i = a; i < b; i++)
#define pre(i, a, b) for(int i = b; i >= a; i--)
using namespace std;
const int N = 110, M = 1e5 + 10;
int n, ans = 0;
int a[N];
bool st[M];
void dfs(int u, int sum)
{
if(!st[sum] && sum > 0) ans++, st[sum] = true;
if(u == n + 1) return ;
dfs(u + 1, sum + a[u]);
dfs(u + 1, sum - a[u]);
dfs(u + 1, sum);
}
int main()
{
cin >> n;
rep(i, 1, n) cin >> a[i];
dfs(1, 0);
cout << ans << endl;
return 0;
}
参考代码2(dp)---- O(nm)
#include <iostream>
#include <cstdio>
#include <set>
#include <map>
#include <vector>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <algorithm>
#include <unordered_map>
#define LL long long
#define rep(i, a, b) for(int i = a; i <= b; i++)
#define reps(i, a, b) for(int i = a; i < b; i++)
#define pre(i, a, b) for(int i = b; i >= a; i--)
using namespace std;
const int N = 110, M = 1e5 + 10;
int n, m;
int a[N];
int f[N][M];
int main()
{
cin >> n;
rep(i, 1, n) cin >> a[i], m += a[i];
rep(i, 1, n)
rep(j, 1, m)
{
if(a[i] == j) f[i][j] = 1;
else f[i][j] = f[i - 1][j] | f[i - 1][abs(j - a[i])] | f[i - 1][j + a[i]];
}
int ans = 0;
rep(i, 1, m)
if(f[n][i]) ans++;
cout << ans << endl;
return 0;
}
边栏推荐
- 基于apache-jena的知识问答
- Postman uses scripts to modify the values of environment variables
- NPM an error NPM err code enoent NPM err syscall open
- Tcp/ip protocol (UDP)
- CSDN question and answer tag skill tree (I) -- Construction of basic framework
- A trip to Macao - > see the world from a non line city to Macao
- [C language foundation] 04 judgment and circulation
- MySQL的一些随笔记录
- 报错解决 —— io.UnsupportedOperation: can‘t do nonzero end-relative seeks
- Use dapr to shorten software development cycle and improve production efficiency
猜你喜欢
Did you forget to register or load this tag 报错解决方法
自动机器学习框架介绍与使用(flaml、h2o)
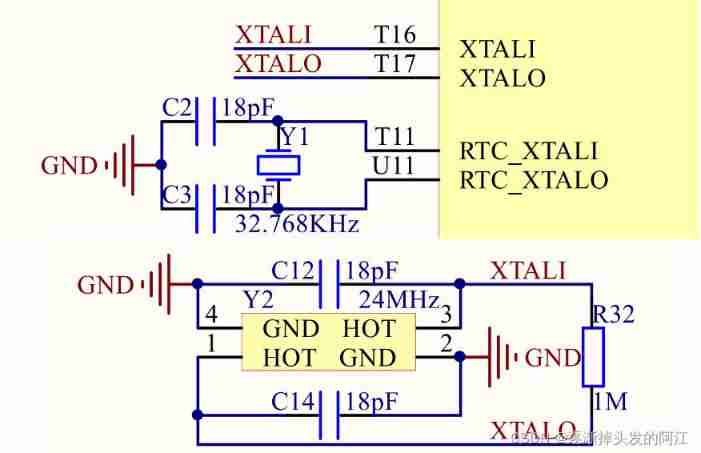
1. Mx6u learning notes (VII): bare metal development (4) -- master frequency and clock configuration
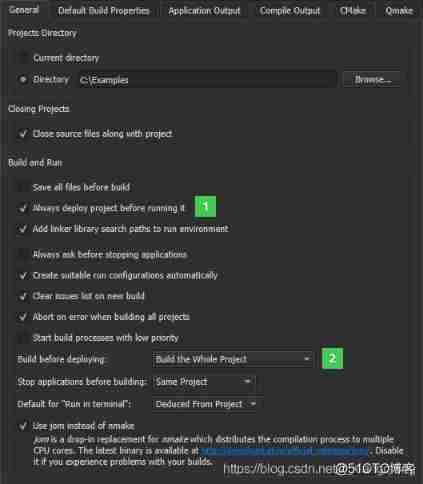
QT creator custom build process
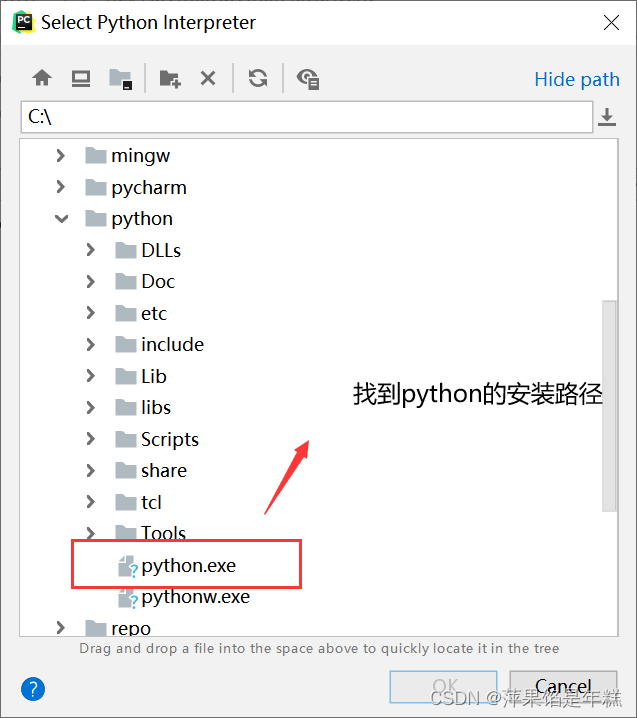
Unable to call numpy in pycharm, with an error modulenotfounderror: no module named 'numpy‘
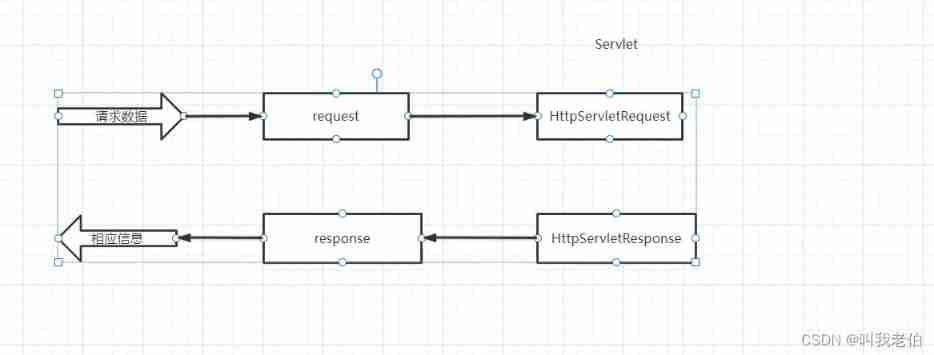
Request object and response object analysis

AI benchmark V5 ranking
【博主推荐】C# Winform定时发送邮箱(附源码)

Data dictionary in C #
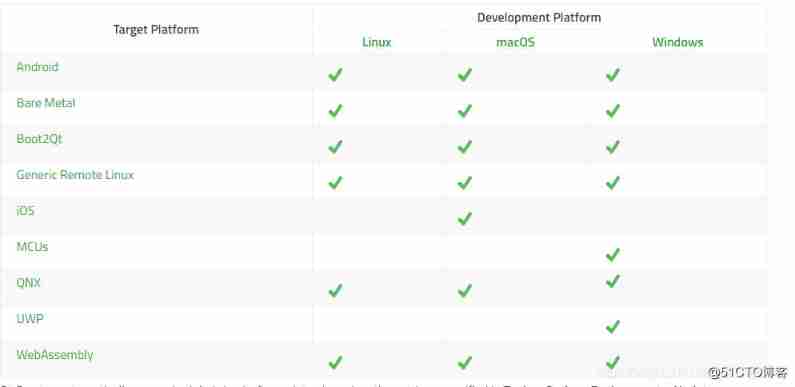
QT creator support platform
随机推荐
Postman environment variable settings
02 staff information management after the actual project
When you open the browser, you will also open mango TV, Tiktok and other websites outside the home page
虚拟机Ping通主机,主机Ping不通虚拟机
Request object and response object analysis
数数字游戏
The virtual machine Ping is connected to the host, and the host Ping is not connected to the virtual machine
自动机器学习框架介绍与使用(flaml、h2o)
error C4996: ‘strcpy‘: This function or variable may be unsafe. Consider using strcpy_s instead
Redis的基础使用
Introduction to the easy copy module
Deoldify项目问题——OMP:Error#15:Initializing libiomp5md.dll,but found libiomp5md.dll already initialized.
SSM整合笔记通俗易懂版
打开浏览器的同时会在主页外同时打开芒果TV,抖音等网站
Installation and use of MySQL under MySQL 19 Linux
Classes in C #
学习问题1:127.0.0.1拒绝了我们的访问
记一次某公司面试题:合并有序数组
In the era of DFI dividends, can TGP become a new benchmark for future DFI?
Some notes of MySQL